結構読まれてるみたいで嬉しいです。ラボの人が意外と手伝ってくれないのはちょっと悲しいです ![]()
A* を直接改変した手法として、 アルゴリズム B 、C、B' 及び BPMX と呼ばれるアルゴリズムを紹介します。B' は、今ではPathmaxとして知られている手法です。BPMX(Bidirectional Pathmax) はPathmaxをさらに改善した手法です。
Introduction
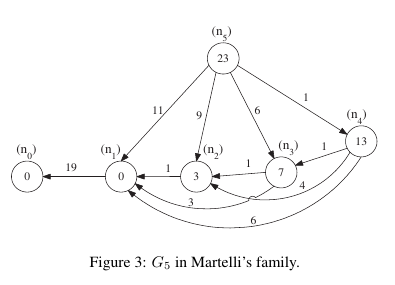
全ての動機は、二日前に紹介した Inconsistent Heuristics にあります。おさらいですが、Martelliは、下に示したような多くの騙し構造をもつグラフの族 $G_N (N\geq 3)$ では、A*が $O(2^N)$ の展開を強いられることを示しました。図は$G_5$の例で、スタートは$n_5$, ゴールは$n_0$, 丸の中の数字はinconsistent な h の値を示しています。この図では、$n_1$ は 8回($=2^{5-2}$)展開されます。同様に$G_6$では、$n_4$ の右にもうひとつ同じようなノードが加わり、$n_1$は16回展開されます。これを検証するのは読者の皆さんにお任せします。
ある一時期までは、例えば (Pearl 1984) にもあるとおり、多くの「自然な」ヒューリスティクスはConsistentであるらしいと考えられてきました。そのため、Inconsistentなヒューリスティクスの採用は永らく避けられて来ました。
しかし、現在では、数多くのInconsistentなヒューリスティクスが提案されていて、実際にある程度使えるということが解っています。
例: 複数のhから毎回ランダムに選ぶ手法 (Zahavi et al, AAAI-07)
ヒューリスティクスには問題ごとに性能・正確さの良し悪しがあります。たとえば、横に細長い地図では $h_x$ は$h_y$ より情報量が多いでしょうし、逆に縦に長い地図では $h_y$のほうが優れているでしょう。
- おさらい: 地図において、 x座標の差の絶対値 $h_x=|v_{gx}−n_x|$ は許容的。
- おさらい: 地図において、 y座標の差の絶対値 $h_y=|v_{gy}−n_y|$ は許容的。
このような2つのヒューリスティクスを組み合わせる手法の話を一度したのを覚えていますか? 2つのmax を取るようなヒューリスティクスです。この手法はadmissibility, consistencyを保存します。
$h_{\max}(n)=\max{h_x(n),h_y(n)}$
ですが、この手法では、値を得るために $h_x,h_y$ を両方計算しなくてはいけません。仮にそれぞれのhが重い計算を要する関数の場合、これは労力に見合わないかもしれません。そこで、もう1つの手法として、毎回一様ランダムに選んだどちらか片方を計算する、というものが考えられます。
$h_{rand}(n) = (rand(0,1) < 0.5) \quad ? \quad h_x(n) \quad : \quad h_y(n)$
この場合、関連のない全く別のヒューリスティクスのh値が1つのグラフに共存するので、探索はinconsistentになります。しかしそのかわり、$h_{\max}$ とくらべてこの関数はつねにどちらか一方の関数しか計算しませんので、関数一回の計算コストを下げつつ、かつ平均的には見積もり値を同等に保つことが出来ます。従って、うまくinconsistencyに対処しさえすれば、平均的に$h_x$または$h_y$のどちらか片方のみよりは良い結果を出しそうです。
アルゴリズムB
このAの欠点を補うのがアルゴリズム$B$ (Martelli 1977) です。$B$は、Aの通常の展開ルール: 「最も小さなfを持つノードを展開」 を行う前に、騙し構造を持つノードが無いかどうかを検査します。
アルゴリズムBの展開ルール: (大域変数F, 初期値は0)
- If OPENに $f(n) < F$ であるノードが存在した場合:
- その中からgの最も小さいノードを選択して展開する。
- Else:
- 最小の$f(n)$を持つノードを展開する。
- $F\leftarrow f(n)$.
大域変数$F$は、現時点で展開された最大の$f(n)$を記録している変数であると言えます。この$F$よりも$f(n)$が小さいopenノードでは、$h$自体はすでに計算されており、問題となるのはそれらのノードのgが真の最小コストg*になっていないことだけです。
通常のA*は、$f<F$ であるノードであっても $f=g+h$ の順にノードを展開してしまい、そのゆえに同じノードを最悪で指数的に多い回数reopenしてしまいます。一方Bは、$f<F$の範囲で$h$を無視し、$g$の更新・最小化に注力します。このことから、Bは Martelli のグラフを 最悪 $O(N^2)$ のreopenで解くことが出来ます。
アルゴリズム B' : Pathmax
(Mero 1984) は、上記のBに改良を加え、Martelliのグラフを最悪O(N)で解くことの出来るB'を開発しました。B'は概念的にはBの改良ですが、結果としてできるアルゴリズムでは $f<F$ となる可能性が消えるので、実質的にはA*の改良です。B'は、ノードの展開後、展開された親ノードを$n$,親の生成した子ノードを$m$として、以下のような操作をします (Zhang et al, IJCAI-09より)。
- $ h(m) \leftarrow \max (h(m), \quad h(n)-cost(n,m))$ .
- $ h(n) \leftarrow \max (h(n), \quad \min_{m\in children(n)} (h(m) + cost(n,m))$ .
1番めのルールは、両辺に $g(n)+cost(n,m)$ を加えれば、 $f(m)\leftarrow \max (f(m), f(n))$ となります。このことからわかるのは、 $f(m)<f(n)$ というinconsistencyが現れた時に、B'は親の$f$値を用いて子を修正する働きを持つということです。
2番目のルールは、両辺に $g(n)$ を加えれば、親と子の$f$値の最大値を用いていることがわかりますが、今度は親のほうを修正しようとしています。
1番めと2番目に共通するのは、ノードnのf値を、スタートからnを通って最も良いfを持つノードに至る経路上のfの最大値で書き換えているということです。この性質から、B'はよりわかりやすく近年ではPathmaxと呼ばれています。
アルゴリズムC (Bagchi, Mahanti 1983)
これはBのFの比較を$<$から$\leq$に変えただけのものです。省略。
Bidirectional Pathmax (BPMX) (Felner et al. 2011)
Pathmaxをさらに改良した手法として、BPMXがあります[1]。Pathmaxの問題点は、探索中に親子の関係にあるノードにしかf最大化操作を行わないことです。しかし、概念的に、f最大化はそのノードから到達可能などのノードに伝播させてもよいはずです。そこで、mから到達可能なノードnについて、ルール1と同様の以下の更新操作を適用します。この更新操作は再帰的にまた$n$に適用します。$n$の子である$l$にも適用し、その子の$k$にも適用し・・・と伝播していきます。
3.. $ h(n) \leftarrow \max (h(n), \quad h(m)-cost(m,n))$ .
この伝播が行われるのは、予め設定した深さの最大値に至るか、あるいはノードを大きい値で更新できなくなるまでです。深さの最大値を無限大としたBPMXをBPMX∞ 、最大値が定数kのBPMXをBPMXk と呼びます。
1: Felner et al. Inconsistent heuristics in theory and practice. Artificial Intelligence 175 (2011) 1570–1603
で、性能は? 実験結果 (Zhang et al, IJCAI-09)
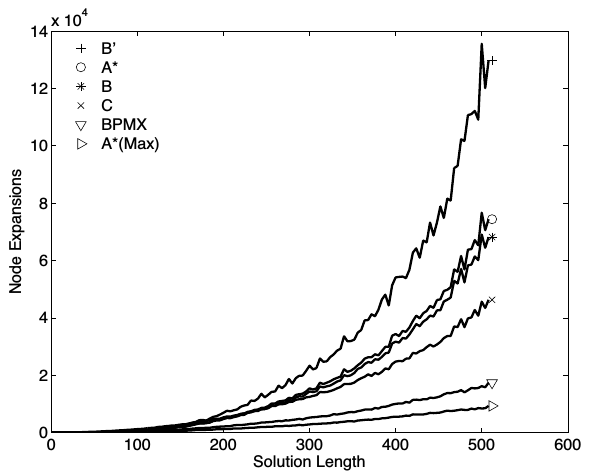
(Zhang et al, IJCAI-09) に、これらのAにおける性能評価が乗っています。実験には、8-connected grid (縦横斜めの格子での経路探索) を用いました。用いたヒューリスティクスは、 consistentなH個のヒューリスティクス $h_i, 0 < i < H$ をランダム選択手法でinconsistentに組み合わせたものです。比較実験として、H個の maxをとるヒューリスティクス (おさらい: 一回の計算にH個全ての計算が必要) を用い、 A(Max)として載せています。縦軸は展開されたノードの数を示しており、実行時間ではありません。
想定通りA*(Max)は最も少ないノード展開数で終了しています(しかし、一回の展開が遅いので、全体として速いかどうかは言えません)。次にA*+BPMXがきており、BPMXがとても効果的であることを示しています。BはAと比べて少ししか改善していません(あるいは、Aが健闘している)。一方、意外なことに、B'(Simple Pathmax) は最も悪い結果でした。このことについてZhang らはTiebreakingルール(同じf値を展開する際にどうするか)に依るものと結論づけています。この詳細については触れません。
このグラフからは、 普通のAと B がそこまで性能が変わらないらしいことがわかります。これは「Aはとんでもなく悪い」という前評判とは異なりますね? じつは、このことは説明できます。
Zhangらは、 Martelli のグラフが「辺のコストが指数的に偏っている」という特徴を持つことを指摘し、「辺のコストがほぼ平坦なグラフでは、 A*の $O(2^N)$ 現象は発生しない」ことを示しました。つまり、たいていのグラフ探索問題では、こういう変なことはおきないということなのでした。
まとめ
- inconsistent heuristics を用いるためのB,B',C,BPMXを紹介した。
- 辺のコストの分布が平坦な普通のグラフでは(例えば全部の辺がコスト1のグラフ)、A*+inconsistentでも十分な性能が出る。
- A*+BPMXならばさらによい性能が出る。
- A* with max heuristics はそれぞれのhの計算がとても重い場合には使えない。(これを裏付ける例は次回IDA*でお見せします)
でした。
Appendix
こういうA*周りの話は、 昔は 京都大学教授の石田先生がKorf先生と共著していたり(Moving Target Search, IJCAI 1991)したのですが、今の日本ではほとんどだれもやっていません。AAAI,IJCAIの過去論文漁っても、この分野で日本人の名前が全然でてこないんですもの。九州大学の横尾先生は分散探索アルゴリズムをやっていたらしいですが、いまではすっかりAAMASの人です。あと残っているのは、SAT/CSP関連の人ばかり? (SAT/CSP: 変数割り当てのための木探索が中心。) この分野ではMIT CSAIL/CMU/NASA Ames/JPLで100人以上の研究者がバリバリやってるのに、日本ではうちの研究室だけ!
人気がないのは第五世代コンピュータのせいかもしれませんが、あのころは深さ優先後ろ向き全探索+手書きのcut+prologでやろうとしていたので、今とは全然アルゴリズムのレベルが違います。ある意味、早すぎたプロジェクトだったと言うべきでしょう。ディープラーニングの技術が枯れて完成したら、つぎに来るのは「現実世界から画像認識したラベル(犬とか猫とかルールとか)」を用いて論理推論/探索を行う人工知能です。推論/探索は、認識と学習とは直行した技術。現在の認識結果、過去の学習結果を用いて将来の可能性を推論するのは探索の仕事にほかありません。