PRMLでは、様々なモデルの最尤推定解を求める際にラグランジュ未定乗数法を使用する。
ラグランジュ未定乗数法の説明はPRMLの付録Eに書いてあるが、拘束条件が不等式の場合(不等式制約)の説明が非常にあっさりと書いてあったので、この記事では、ラグランジュ未定乗数法の拘束条件が不等式の場合をもう少し詳しく解説する。
問題設定
問題設定はPRMLの付録Eにある通りで、ある$D$次元の変数$\mathrm{\boldsymbol{x}}=(x_1, x_2, \cdots , x_D)^{\mathrm{T}}$を考え、その変数$\mathrm{\boldsymbol{x}}$をスカラーに変換する関数$f(\mathrm{\boldsymbol{x}})$と$g(\mathrm{\boldsymbol{x}})$を用意する。
この設定の下で、以下の$2$つの問題を考える。
- 領域$g(\mathrm{\boldsymbol{x}}) \geq 0$内での関数$f(\mathrm{\boldsymbol{x}})$の最大値を与える点を求める問題(このとき$f(\mathrm{\boldsymbol{x}})$は上に凸な関数と仮定)
- 領域$g(\mathrm{\boldsymbol{x}}) \geq 0$内での関数$f(\mathrm{\boldsymbol{x}})$の最小値を与える点を求める問題(このとき$f(\mathrm{\boldsymbol{x}})$は下に凸な関数と仮定)
これらの問題の解き方をそれぞれ解説していく。
最大値問題
まずは、領域$g(\mathrm{\boldsymbol{x}}) \geq 0$内での関数$f(\mathrm{\boldsymbol{x}})$の最大値を与える点を求める。
以下の画像の黄土色の領域を$g(\mathrm{\boldsymbol{x}}) >0$の領域とし、$g(\mathrm{\boldsymbol{x}}) =0$なる領域(曲線)を赤い線とする。
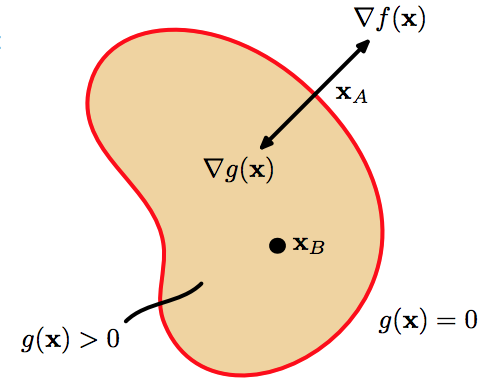
ここで領域$g(\mathrm{\boldsymbol{x}}) \geq 0$内での関数$f(\mathrm{\boldsymbol{x}})$の最大値を与える点$\mathrm{\boldsymbol{x}}_{\mathrm{max}}$を以下の$2$つの状況で場合分けをする。
- $g(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) > 0$
- $g(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) =0$
1の場合
この場合、$\mathrm{\boldsymbol{x}}_{\mathrm{max}}$は$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})=\boldsymbol{0}$を満たすことを解説する。
解説
$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})\ne \boldsymbol{0}$であると仮定する。
$\mathrm{\boldsymbol{x}}_{\mathrm{max}}$から十分に近い点$\bar{\mathrm{\boldsymbol{x}}}=\mathrm{\boldsymbol{x}}_{\mathrm{max}}+\boldsymbol{\mathrm{\epsilon}}$を考える。(十分近い点とは、$g(\bar{\mathrm{\boldsymbol{x}}}=\mathrm{\boldsymbol{x}}_{\mathrm{max}}+\boldsymbol{\mathrm{\epsilon}}) > 0$であるくらい近い点という意味。)
このとき、$f(\bar{\mathrm{\boldsymbol{x}}})$は
f(\bar{\mathrm{\boldsymbol{x}}}) \sim f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})+\boldsymbol{\mathrm{\epsilon}}^{\mathrm{T}}\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) \tag{1}
と近似できる。
$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})\ne \boldsymbol{0}$であるので、$\boldsymbol{\mathrm{\epsilon}}$を$\boldsymbol{\mathrm{\epsilon}}^{\mathrm{T}}\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) > 0$となる方向にとれば、式(1)より
f(\bar{\mathrm{\boldsymbol{x}}}) > f(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) \tag{2}
となる。
式(2)と条件$g(\bar{\mathrm{\boldsymbol{x}}}) > 0$は、$\mathrm{\boldsymbol{x}}_{\mathrm{max}}$が領域$g(\mathrm{\boldsymbol{x}}) \geq 0$内での関数$f(\mathrm{\boldsymbol{x}})$の最大値を与える点であることに矛盾する。
よって、仮定$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})\ne \boldsymbol{0}$は間違っており、$\mathrm{\boldsymbol{x}}_{\mathrm{max}}$は
\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})=\boldsymbol{0}\tag{3}
を満たすことがわかる。
2の場合
この場合は、$\mathrm{\boldsymbol{x}}_{\mathrm{max}}$は(ある正の定数$\lambda$が存在して、)$\nabla f(\mathrm{\boldsymbol{x}})=-\lambda \nabla g(\mathrm{\boldsymbol{x}})$を満たす点であることを解説する。
解説
まず、ベクトル$\nabla g(\mathrm{\boldsymbol{x}})$の方向について解説する。
$g(\mathrm{\boldsymbol{x}})=0$上の非常に近い2点$\mathrm{\boldsymbol{x}}$と$\mathrm{\boldsymbol{x}}+\boldsymbol{\mathrm{\epsilon}}_{g}$を考える。
つまり、$\mathrm{\boldsymbol{x}}$と$\mathrm{\boldsymbol{x}}+\boldsymbol{\mathrm{\epsilon}}_{g}$は$g(\mathrm{\boldsymbol{x}})=g(\mathrm{\boldsymbol{x}}+\boldsymbol{\mathrm{\epsilon}}_{g})=0$を満たす。
ここで、$g(\mathrm{\boldsymbol{x}}+\boldsymbol{\mathrm{\epsilon}}_{g})$に対して、式(1)と同じ近似を用いると、
g(\mathrm{\boldsymbol{x}}+\boldsymbol{\mathrm{\epsilon}}_{g}) \sim g(\mathrm{\boldsymbol{x}})+\boldsymbol{\mathrm{\epsilon}}^{\mathrm{T}}_{g}\nabla g(\mathrm{\boldsymbol{x}}) \tag{4}
を満たすので、$g(\mathrm{\boldsymbol{x}})=g(\mathrm{\boldsymbol{x}}+\boldsymbol{\mathrm{\epsilon}}_{g})$より、
\boldsymbol{\mathrm{\epsilon}}^{\mathrm{T}}_{g}\nabla g(\mathrm{\boldsymbol{x}})=0 \tag{5}
であることがわかる。
ここで、$\boldsymbol{\mathrm{\epsilon}}_{g}$は$g(\mathrm{\boldsymbol{x}})=0$に沿ったベクトルなので、$\nabla g(\mathrm{\boldsymbol{x}})$は$g(\mathrm{\boldsymbol{x}})=0$に垂直なベクトルである。
さらに、$\boldsymbol{\mathrm{\epsilon}}_{g}$を$g(\mathrm{\boldsymbol{x}})=0$に沿ったベクトルではなく、垂直なベクトル$\boldsymbol{\mathrm{\epsilon}}_{g}=\nabla g(\mathrm{\boldsymbol{x}})$ととると、式(4)より
g(\mathrm{\boldsymbol{x}}+\boldsymbol{\mathrm{\epsilon}}_{g}) \sim g(\mathrm{\boldsymbol{x}})+\| \nabla g(\mathrm{\boldsymbol{x}})\|^2 \tag{6}
となる。
よって、$g(\mathrm{\boldsymbol{x}}+\boldsymbol{\mathrm{\epsilon}}_{g}) > g(\mathrm{\boldsymbol{x}})$となるので、$\nabla g(\mathrm{\boldsymbol{x}})$は$g(\mathrm{\boldsymbol{x}})$が増える方向、つまり$g(\mathrm{\boldsymbol{x}}) > 0$の方向を向く。
また、$g(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) =0$を満たす点$\mathrm{\boldsymbol{x}}_{\mathrm{max}}$に対して、$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$も$g(\mathrm{\boldsymbol{x}})=0$に垂直でないといけないことがわかる。
なぜなら、垂直でないとすると、$g(\mathrm{\boldsymbol{x}})=0$の面に沿って、$f(\mathrm{\boldsymbol{x}})$値がさらに大きくなるような点$\mathrm{\boldsymbol{x}}$をとるように動かせるからである。
以上より、$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$と$\nabla g(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$は平行なベクトルである。
ただし、$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$は領域$g(\mathrm{\boldsymbol{x}}) > 0$の外へと向く方向のベクトルでないといけない。
なぜなら、$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$が領域$g(\mathrm{\boldsymbol{x}}) > 0$に向いていたとすると、$g(\mathrm{\boldsymbol{x}}) > 0$の中に$f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$より大きい値が存在することになるからである。
よって、$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$と$\nabla g(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$はある正の定数$\lambda$を用いて、
\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) = -\lambda \nabla g(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) \tag{7}
となる。
1の場合と2の場合のまとめ
1の場合と2の場合をまとめた式は以下のようになる。
\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) = -\lambda \nabla g(\mathrm{\boldsymbol{x}}_{\mathrm{max}})\\
g(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) \geq 0\\
\lambda \geq 0 \\
\lambda g(\mathrm{\boldsymbol{x}}_{\mathrm{max}})=0
もし、$g(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) > 0$の時(1の場合)は$\lambda g(\mathrm{\boldsymbol{x}}_{\mathrm{max}})=0$より、$\lambda=0$なので、式(3)$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) =\mathrm{\boldsymbol{0}}$を満たす。
一方、$g(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) = 0$の時(2の場合)は式(7)$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) = -\lambda \nabla g(\mathrm{\boldsymbol{x}}_{\mathrm{max}})$が成り立つ。
これを別の方法で表現すると、ラグランジュ関数$L(\mathrm{\boldsymbol{x}}, \lambda)$
L(\mathrm{\boldsymbol{x}}, \lambda)=\nabla f(\mathrm{\boldsymbol{x}})+\lambda \nabla g(\mathrm{\boldsymbol{x}})
を以下の条件
g(\mathrm{\boldsymbol{x}}) \geq 0\\
\lambda \geq 0 \\
\lambda g(\mathrm{\boldsymbol{x}})=0
で最大化することに帰着する。
この条件をKKT条件という。
最小値問題
最大値問題との違いは、$g(\mathrm{\boldsymbol{x}}_{\mathrm{min}}) =0$となる場合で、最大値問題と同様に$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{min}})$と$\nabla g(\mathrm{\boldsymbol{x}}_{\mathrm{min}})$は平行である必要があるが、$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{min}})$は領域$g(\mathrm{\boldsymbol{x}}) > 0$の内側へと向く方向のベクトルでないといけない。
なぜなら、$\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{min}})$が領域$g(\mathrm{\boldsymbol{x}}) > 0$の外側に向いていたとすると、$g(\mathrm{\boldsymbol{x}}) > 0$の中に$f(\mathrm{\boldsymbol{x}}_{\mathrm{min}})$より小さい値が存在することになるからである。
よって、
\nabla f(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) = -\lambda \nabla g(\mathrm{\boldsymbol{x}}_{\mathrm{max}}) \tag{8}
となる。
以上より、最小値問題ではラグランジュ関数$L(\mathrm{\boldsymbol{x}}, \lambda)$
L(\mathrm{\boldsymbol{x}}, \lambda)=\nabla f(\mathrm{\boldsymbol{x}})-\lambda \nabla g(\mathrm{\boldsymbol{x}})
を以下の条件(KKT条件)
g(\mathrm{\boldsymbol{x}}) \geq 0\\
\lambda \geq 0 \\
\lambda g(\mathrm{\boldsymbol{x}})=0
で最小化することに帰着する。