出典
H3: Uber’s Hexagonal Hierarchical Spatial Index (2018/06/27)
筆者
Isaac Brodsky
Isaac Brodsky is a software engineer on Uber’s Marketplace Intelligence team.
Uberとは
Uberホームページ
世界を席巻しつつある白タクサービス、宅配のUber Eats、オンデマンドフライトのUberAIRなどで生活を変えようとしている。
日本進出はソフトバンクがサポート
参考:ソフトバンク、ウーバーへの出資完了
H3とは
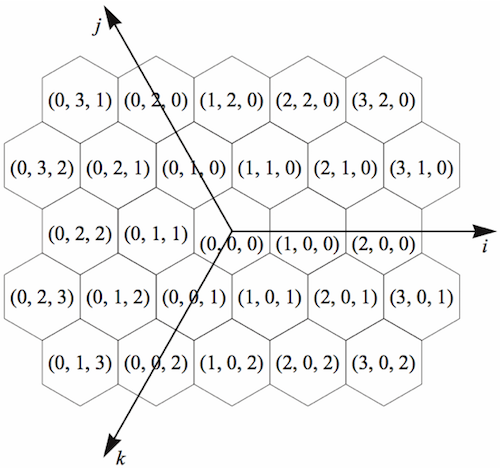
大小様々な六角形をグリッドとする新しいインデックスシステム(座標システム)
(「大小様々な六角形」、「階層的な六角形」の説明は後ほど)
本文
※意訳している部分があるので、引用元も参照ください。
なぜH3
地図などの空間データセットを解析する際に、グリッドシステムは重要となります。ここでのグリッドシステムとは、地球の表面をどのようなグリッドに分割する仕組みです。
このことを踏まえ、UberがH3を開発したのは以下を可能にするグリッドシステムを実現するためです。
- 乗車料金と乗車経路の最適化
- 空間データの視覚化と探求
H3を使えば地理情報の解析ができます。都市レベルで動的な価格設定をするなどの意思決定に繋がります。Uberは市場の分析、最適化のためにH3を使います。H3はこのためのデザインされ、我々が階層的な六角形を使うことに繋がりました。
オープンソース化
今年(2018年)のはじめ、UberはGithub上でH3をオープンソース化しました。
そして先週、H3 JavaScriptを公開しました。
記事の目的
この記事では「H3の特徴であるグリッドシステムをなぜ使うのか」、「H3のスタートガイド」について話していきます。
背景
毎日、何百万というイベント(注文)がUberに届きます。車に乗りたい人はリクエストをし、ドライバーは運転を開始します。お腹が減った人はご飯を注文します。それらのイベントはどこかの場所で起こっています。例えば、乗客は自宅から乗車リクエストを送るかもしれませんし、ドライバーはそのリクエストを数マイル離れた社内で承認するかもしれません。
これらのイベントの情報はサービスを通じてUberがユーザー市場を理解し最適化することに役立ちます。例えば、市のある地域では需要が供給を超え、それに応じて値段が変わるかもしれません。もしくは、uberPOOL(乗り合いサービス)のドライバーと2つの乗車リクエストがとても近いことを教えてくれるかもしれません。
Uber市場のデータから情報、洞察を得るには、市内全域のデータを解析する必要があります。なぜなら市は地理的に多様性があり、細かな粒度で分析をしなければいけません。しかし、「イベントが起きた場所を正確に(点で)求めるといった」最高精度の分析は難しい上にコストが高くなります。そのため、エリアの分析がずっと実用的です。
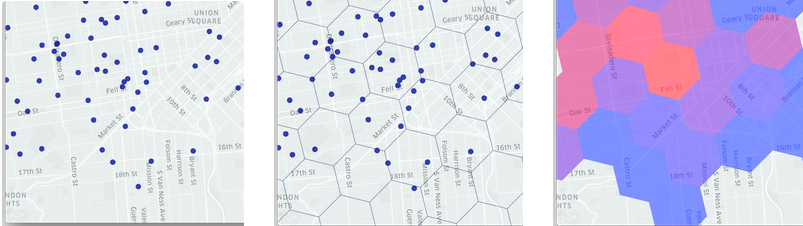
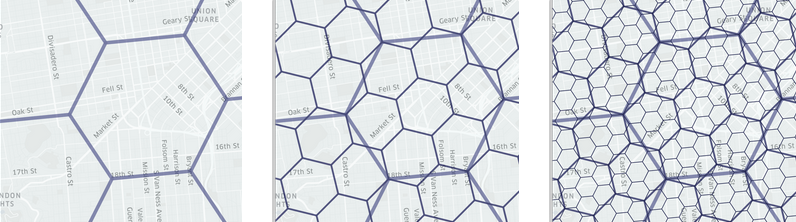
画像は点情報がエリアの情報に変わっていく様子。(市内の車→六角形内の車→車の数で六角形を色付け)
グリッドシステムはイベントを六角形エリア(セル)に入れるために使われています。データポイントは六角形に詰め込まれているので、六角形に詰め込まれたデータを使えばデータポイントを表現する事が可能となります。例えば、、私達はサービスを展開する市の六角形内にある需要供給を測ることにより、値段の上昇を計算します。六角形は、Uberの市場分析における基礎となるのです。
なぜ六角形か
六角形であることも大切です。市内の利用者はたいてい動いており、六角形はユーザーが市内を移動する際に生じる量子化誤差(情報を連続(アナログ)から離散(デジタル)に変えるときに生じる誤差)を最小化します。また、簡単に半径を近似することも可能にします。
例:Engineering Uber Predictions in Real Time with ELK
六角形以外の選択肢として、以下も可能でした。
多角形
郵便番号を用いたエリア分けはその例ですが、いびつで分析には使いづらい大きさで、さらには私達の意図とは関係なく変更される可能性もあります。(画像はマンハッタンのZIPコード(郵便番号)マップ)
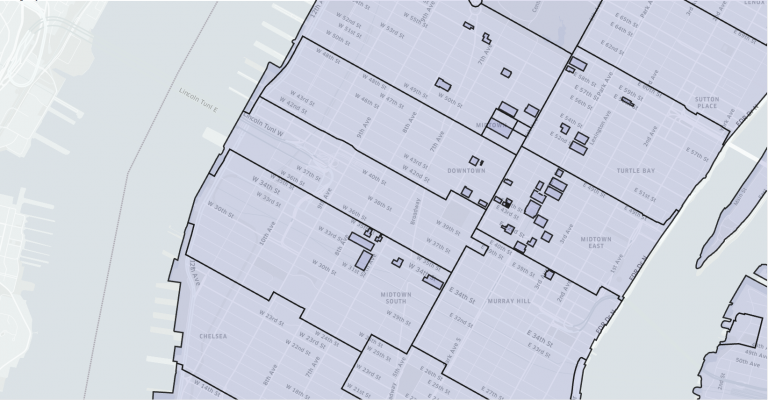
Uberオペレーターの経験によるマッピング
→街の変化によるアップデートが必要で、エリアの境目を決めるのも大変
(属人的でコストも高い)
グリッドシステムはUberがサービスを展開する市内で比較可能な形と大きさをもっており、属人的な変更も必要ありません。グリッドシステムは道路や市内の地域を並べることはしませんが、一方でグリッドをクラスタリングする(まとめる)ことによって、効率的に地域を表すことができます。クラスタリングをすることによって、分析はより便利なものになります。
H3
Uberは六角形のグリッドシステムと階層的インデックスシステムのいいどこ取りをするためにH3を開発しました。
地球にグリットシステムを適用する場合、考えなければいけないことは少なくとも2つ:
- 地図の投影
- 地図上のグリッド
地図の投影
地球上の位置という3次元の情報を地図上の点という2次元の情報にすること
地球上のグリッド
2次元にした後、地球のグリッドシステムに則りグリッドが加えられます。
様々な投影法・グリッドの組み合わせは無限にあります。メルカトル図法と正方グリッドは有名な例です。この組み合わせは使えないことはないですが、多くの欠点があります。まず、メルカトル図法が生むサイズの歪みは見逃せません。いくつかのセルはかなり異なるエリアを含むでしょう。正方グリッドにも、分析の際に複数の係数のセットが必要であるという欠点があります。この原因となるのは、正方グリッドの幾何学的性質、隣接する図形が2種類あることにあります。辺を共有する部分が4方向と頂点を共有する部分が4方向にあるのです。
選ばれたのは
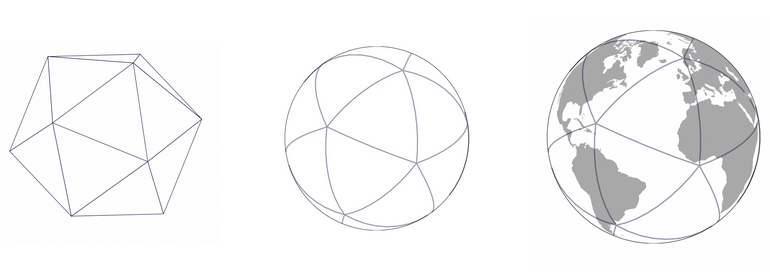
投影方法としては心射方位図法が選べれました。20面体の中心から表面に向けて投影されていると考えてください。
20面体の投影は、20の2次平面を生みます。
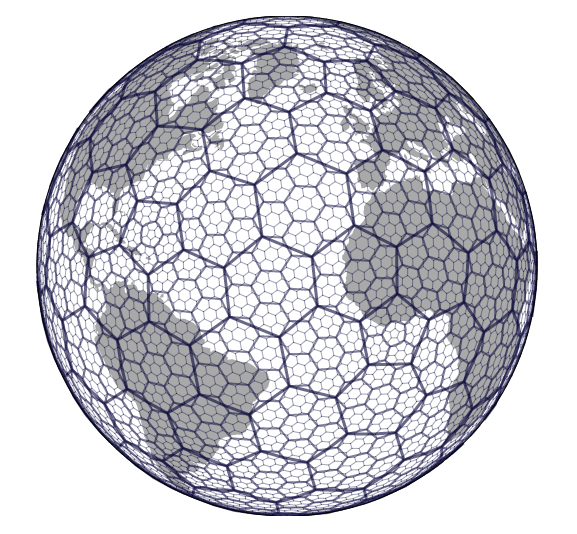
20面体は2次元に広げることが可能ですが、H3はそのようなことをせず、地球の表面にグリッドを残しておきます。(上画像)
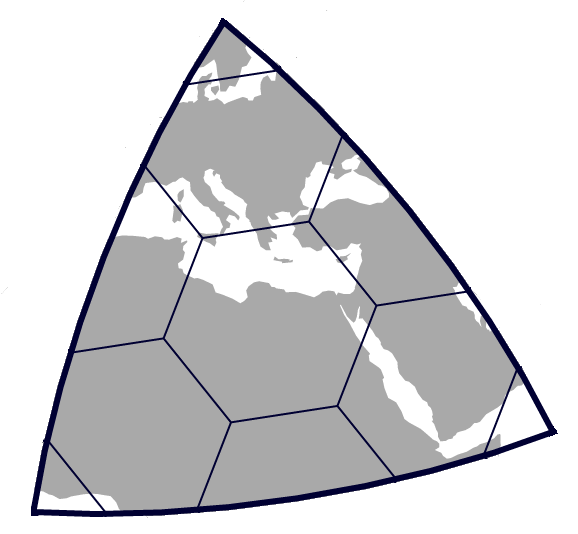
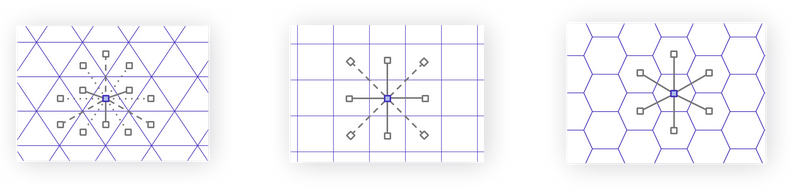
グリッドの形として選ばれたのはもちろん六角形です。下図のように、六角グリッドは隣接するセルへの距離が等しく、全エリアと辺を共有しています。(三角形、四角形を参考)
これは、分析をし勾配を平滑化する際に非常に便利な特性となります。
H3のグリッドは122のベースセルからなっています。重複を無視すると20面体の1つの面につき10の六角形があることになります。いくつかのセルは複数の面にわたって存在します。(下図の境界にあるセルを参考)
20面体を六角形のみで埋めることは不可能なため、12の五角形を導入しました。(サッカーボール、五角形:12個、六角形:20個)20面体の頂点に1つずつ存在します。
H3は16段階の解像度に対応しています。解像度が1段階あがるとセルの大きさが1/7になります。六角形を完璧に7つの六角形に分けることはできないため、解像度が上がったセルは「だいたい」親のセルに含まれていることになります。
これにより、位置の特定が効率的になります。子セルがおおまかにしか親セルにふくまれていないため、位置特定の際にエリアを切り捨てる必要があり、それはエリアの歪みを生みます。
しかし、それ以外の場合では境界は正確に定義されます。
Getting started with H3
H3のインデックスシステムはGithub上で公開されています。ライブラリ自体はC言語で書かれているが、多くの言語に対応しています。はじめての場合Bindingsの利用が推奨されます。Java, JavaScript用のBindingsをUberは公開しており、コミュニティは更に多くの言語に対応するために貢献しています。。PythonとGoのBindingsは近々公開予定。
基本的な関数
- geoToH3: 経度緯度情報を64Bit H3インデックスに変換する、解像度の指定も可能。
- kRing
など
さらなる情報
H3はUberが市場の定量的解析をすることを可能にしています。オープンソース化された今、あなたも世界を六角形化することが可能です!
「Githubのレポジトリをフォロー」し、「#uberH3のタグをつけてツイート」してH3コミュニティに参加してください!