はじめに
この記事は、OUCC Advent Calendar 2020の18日目の記事です。
UnityでShaderを使う際、たいていの場合はテクスチャで図柄を指定することが多いと思います。一方、Shader内に直接色を指定する記述をすることで、テクスチャを使わずに色付けすることもできます。一番単純なものの一つは単色シェーダー。
この記事では、step関数を使い範囲指定をすることで、テクスチャを用いずに図柄を描画する例を紹介します。
初心者の書く初心者向け?記事ですので、細かい点何卒ご容赦願いたく。
環境
Unityのバージョンは2018.4.20f1を使用しています。
描く画像
今回描くのはデジタル時計風の数字です。決してネタになる図形を見つけられなかったわけではない。
完成品はこちら
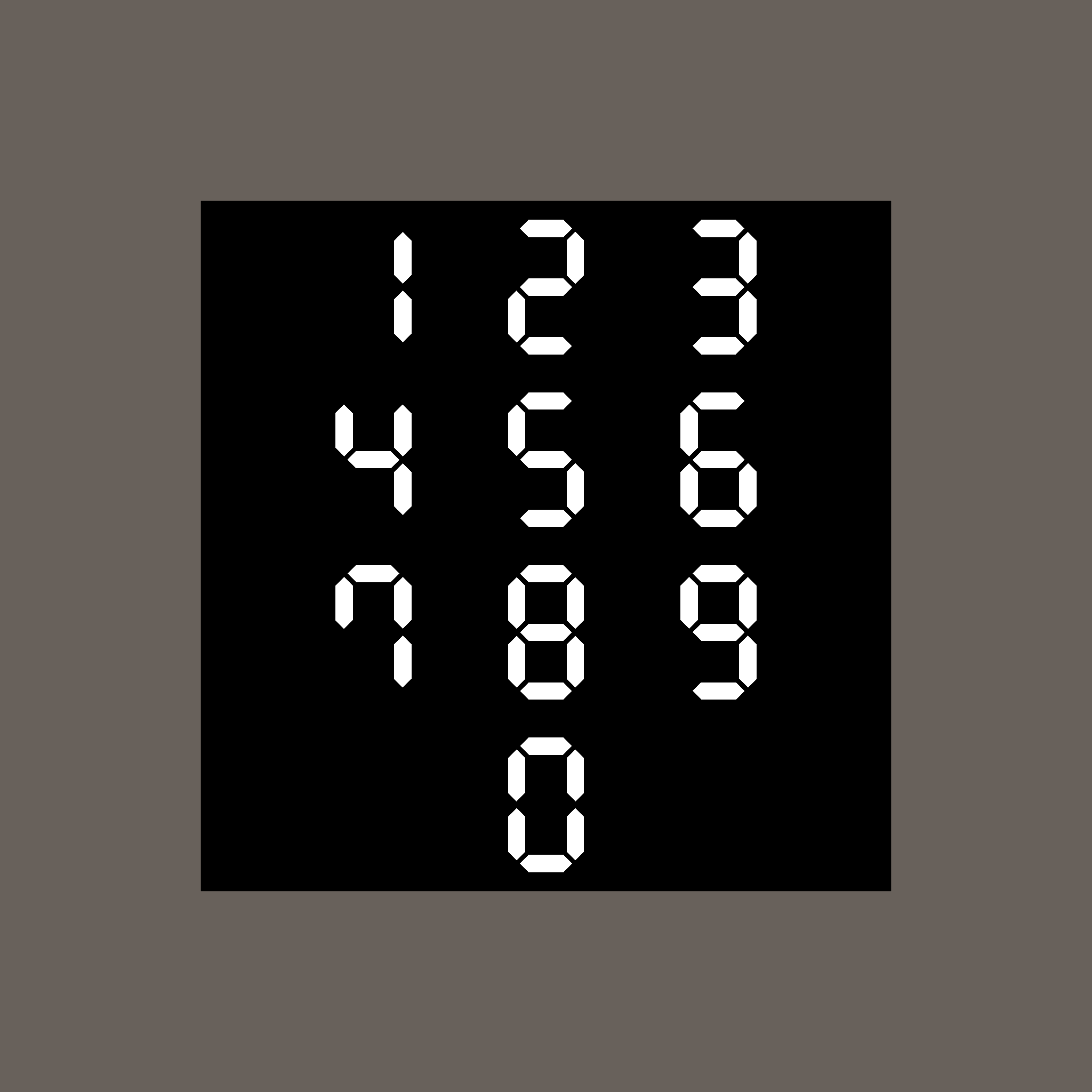
そのため、まずこの図形を描き、その後それらを組み合わせて数字にする、という手順で進めていきます。
準備
Unityを開き、描画対象としてQuadを配置、適当に位置、向き、サイズを調整します。
projectウィンドウで右クリック > Create > MaterialでShaderを適用するマテリアルを作成し、Quadに割り当てます。
続いて同様にCreat > Shader > Unlit ShaderでShaderファイルを作成します。
マテリアルの設定からシェーダーを"Unlit/Shaderファイル名"に変更します。
Quadが真っ白になれば準備完了です。
Shaderファイルを任意のテキストエディタで開きましょう。
Shaderを書く
中身の確認
開いたShaderファイルの中身はこのようになっているはずです。
Shaderファイルの中身(折り畳み)
Shader "Unlit/Numbers"
{
Properties
{
_MainTex ("Texture", 2D) = "white" {}
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
// make fog work
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
};
sampler2D _MainTex;
float4 _MainTex_ST;
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
UNITY_TRANSFER_FOG(o,o.vertex);
return o;
}
fixed4 frag (v2f i) : SV_Target
{
// sample the texture
fixed4 col = tex2D(_MainTex, i.uv);
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
ENDCG
}
}
}
Shaderファイルの準備
まず不要な部分を消しましょう。今回テクスチャは使用しないので、inspectorでテクスチャを指定するための記述と、そのテクスチャを処理する部分を削除します。
Properties で囲われた部分の_MainTex ("Texture", 2D) = "white" {}を削除します。
次いで中ほどにあるsampler2D _MainTex;とfloat4 _MainTex_ST;も削除します。
さらにv2f vert (appdata v)内のo.uv = TRANSFORM_TEX(v.uv, _MainTex);をo.uv = v.uv;に書き換えます。
最後にfixed4 frag (v2f i) : SV_Target内のfixed4 col = tex2D(_MainTex, i.uv);をfixed4 col = fixed4 (1, 1, 1, 1);と書き換えます。
書き換え後の中身(折り畳み)
Shader "Unlit/Numbers"
{
Properties
{
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
// make fog work
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
};
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
UNITY_TRANSFER_FOG(o,o.vertex);
return o;
}
fixed4 frag (v2f i) : SV_Target
{
// sample the texture
fixed4 col = fixed4 (1, 1, ,1 ,1);
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
ENDCG
}
}
}
これでこのShaderはテクスチャを使わず、常に全体を白で塗りつぶすようになりました。
また、UV座標はQuadに対して左下が原点となっているため、描きやすくするため座標をずらして中心に原点を持ってきます。先ほどの続きに改行して、以下の一行を追加します。
fixed4 col = fixed4 (1, 1, 1, 1);
i.uv -= 0.5; //この行を追加
stepについて
さて、図形を描いていく前に先に今回の主役であるstep関数について説明しておきます。
step(a, x)と記述することで、x >= aのとき1を、x < aのときに0を返します。1
図形を描く
いよいよ図形を描いていきます。
色を描画する部分はfixed4 frag (v2f i) : SV_Target内(fragment shader)ですので、以後特に断りの無い場合はこの中の記述と考えてください。
では、六角形を描いていきます。
はじめは斜めの部分は無視して、長方形を描きましょう。
y座標が-0.05 < y < 0.05の範囲のとき1を返すようにしましょう。
-0.05 < yの場合は1 - step(-0.05, i.uv.y)
0.05 > yの場合はstep(0.05, i.uv.y)です。
今これらを同時に満たすときに1が返るようにしたいので、これらを乗算して
step(-0.05, i.uv.y)*(1 - step(0.05, i.uv.y));とします。
乗算することで、少なくともどちらか一方が0、すなわち範囲外のときに0が、両方共が1、すなわち範囲内のときに1が返るようになります。
ここまでをShader内に記述した例がこちらです。
fixed4 frag (v2f i) : SV_Target
{
fixed4 col = fixed4 (0, 0, 0, 1);
i.uv -= 0.5;
col *= step(-0.05, i.uv.y)*(1 - step(0.05, i.uv.y)); //ここ
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
colに乗算することで、範囲外をすべて黒に塗りつぶしています。
さて、では次に六角形にするために適当なところで角を削っていきましょう。
まず、左右を一回ずつ斜めに削って台形にします。
斜めの直線は一次関数 y = x - a(aは定数) で表せますので、この直線より上か下かで範囲内外を切り分けましょう。2
col *= step(-0.05, i.uv.y)*(1 - step(0.05, i.uv.y));
col *= step(i.uv.y, i.uv.x)*step(i.uv.y, -i.uv.x); //この行を追加
としておきます。
このままだと目指す図形にはならないので、それぞれずらしていきましょう。
stepの第二引数(右辺)に0.15を加えて
col *= step(-0.05, i.uv.y)*(1 - step(0.05, i.uv.y));
col *= step(i.uv.y, i.uv.x + 0.15)*step(i.uv.y, -i.uv.x + 0.15); //この行を編集
では続いて六角形を描画していきましょう。
と言っても、斜めに削るのを下側にも付け足すだけです。
切片の正負を逆転させ、1から引いたものを掛け合わせて
(1 - step(i.uv.y, i.uv.x - 0.15))*(1 - step(i.uv.y, -i.uv.x - 0.15))
としたものが追加で削る部分を表します。
colに乗算して
col *= step(-0.05, i.uv.y)*(1 - step(0.05, i.uv.y));
col *= step(i.uv.y, i.uv.x + 0.15)*step(i.uv.y, -i.uv.x + 0.15);
col *= (1 - step(i.uv.y, i.uv.x - 0.15))*(1 - step(i.uv.y, -i.uv.x - 0.15)) //この行を編集
使いまわしをしやすいように、一行にまとめたうえで関数にしましょう。 関数にした部分はfragment shaderの外に書きます。 書き換え後の全体は以下の 通りです。
//前略
//ここを追加
fixed hexa (float2 uv)
{
return step(-0.05, uv.y)*(1 - step(0.05, uv.y))*step(uv.y, uv.x + 0.15)*step(uv.y, -uv.x + 0.15)*(1 - step(uv.y, uv.x - 0.15))*(1 - step(uv.y, -uv.x - 0.15));
}
fixed4 frag (v2f i) : SV_Target
{
// sample the texture
fixed4 col = fixed4 (1, 1, 1, 1);
i.uv -= 0.5;
col.xyz = hexa(i.uv); //この行を編集
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
初めに示した六角形ができると思います。
数字を作る
では、この六角形を組み合わせて数字を作っていきましょう。
"8"が作れれば、あとの数字は不要な部分を削ればいいだけなので、まずは"8"を作りましょう。
説明を簡単にするために、それぞれのパーツに画像のように番号を割り振ります。

それぞれに変数を割り当てます。
以下のように変数を宣言します。
fixed4 col = fixed4 (1, 1, 1, 1);
//ここから追加分
fixed4 numid_1 = fixed4 (1, 1, 1, 1);
fixed4 numid_2 = fixed4 (1, 1, 1, 1);
fixed4 numid_3 = fixed4 (1, 1, 1, 1);
fixed4 numid_4 = fixed4 (1, 1, 1, 1);
fixed4 numid_5 = fixed4 (1, 1, 1, 1);
fixed4 numid_6 = fixed4 (1, 1, 1, 1);
fixed4 numid_7 = fixed4 (1, 1, 1, 1);
//ここで値を代入
//追加
fixed4 num8 = saturate(numid_1 + numid_2 + numid_3 + numid_4 + numid_5 + numid_6 + numid_7);
col = num8; //変更
ここで使っている"saturate(x)"は、0 <= x <= 1 のとき x を、x < 0 のとき 0 を、x > 1 のとき 1 を返します。つまり、xの値が 0~1 の範囲に収まるように端を詰めます。
色を加算しているので、何かの間違いで値が 1 を超えることの無いようにしています。
今回はあまり気にする必要はありません。
1番、4番のパーツ
1番と4番のパーツは、hexaの場所を移動させます。
1番のパーツは上にずらしましょう。
hexa(float2 (i.uv.x, i.uv.y - 0.34))で上のほうに移動します。
4番のパーツは下にずらして、
hexa(float2 (i.uv.x, i.uv.y + 0.34))とします。
これは1番のy座標をずらす向きを逆にしたものです。
1番のパーツをnumid_1に代入します。3
numid_1.xyz = hexa(float2 (i.uv.x, i.uv.y - 0.34));
2番、3番、5番、6番のパーツ
2番、3番、5番、6番のパーツは、hexaのx座標とy座標を入れ替えるとできます。
すなわちhexa(float2 (i.uv.y, i.uv.x))です。
場所を移動させましょう。
2番はhexa(float2 (i.uv.y - 0.17, i.uv.x - 0.17))
3番はhexa(float2 (i.uv.y + 0.17, i.uv.x - 0.17))
5番はhexa(float2 (i.uv.y + 0.17, i.uv.x + 0.17))
6番はhexa(float2 (i.uv.y - 0.17, i.uv.x + 0.17))
でいいでしょう。
7番のパーツ
最後の7番のパーツは、hexaをそのまま使います。
hexa(i.uv)
できた数字
また、足し合わせるnumidを減らすことで、任意の数字を作ることができます。
画像は数字の"7"です。numid_4、numid_5、numid_7を省くことで作れます。

コード前文は以下の通りです。
コード全文(折り畳み)
Shader "Unlit/Numbers"
{
Properties
{
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
// make fog work
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
};
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
UNITY_TRANSFER_FOG(o,o.vertex);
return o;
}
fixed hexa (float2 uv)
{
return step(-0.05, uv.y)*(1 - step(0.05, uv.y))*step(uv.y, uv.x + 0.15)*step(uv.y, -uv.x + 0.15)*(1 - step(uv.y, uv.x - 0.15))*(1 - step(uv.y, -uv.x - 0.15));
}
fixed4 frag (v2f i) : SV_Target
{
fixed4 col = fixed4 (1, 1, 1, 1);
fixed4 numid_1 = fixed4 (1, 1, 1, 1);
fixed4 numid_2 = fixed4 (1, 1, 1, 1);
fixed4 numid_3 = fixed4 (1, 1, 1, 1);
fixed4 numid_4 = fixed4 (1, 1, 1, 1);
fixed4 numid_5 = fixed4 (1, 1, 1, 1);
fixed4 numid_6 = fixed4 (1, 1, 1, 1);
fixed4 numid_7 = fixed4 (1, 1, 1, 1);
i.uv -= 0.5;
numid_1.xyz = hexa(float2 (i.uv.x, i.uv.y - 0.34));
numid_2.xyz = hexa(float2 (i.uv.y - 0.17, i.uv.x - 0.17));
numid_3.xyz = hexa(float2 (i.uv.y + 0.17, i.uv.x - 0.17));
numid_4.xyz = hexa(float2 (i.uv.x, i.uv.y + 0.34));
numid_5.xyz = hexa(float2 (i.uv.y + 0.17, i.uv.x + 0.17));
numid_6.xyz = hexa(float2 (i.uv.y - 0.17, i.uv.x + 0.17));
numid_7.xyz = hexa(i.uv);
fixed4 num1 = saturate(numid_2 + numid_3);
fixed4 num2 = saturate(numid_1 + numid_2 + numid_4 + numid_5 + numid_7);
fixed4 num3 = saturate(numid_1 + numid_2 + numid_3 + numid_4 + numid_7);
fixed4 num4 = saturate(numid_2 + numid_3 + numid_6 + numid_7);
fixed4 num5 = saturate(numid_1 + numid_3 + numid_4 + numid_6 + numid_7);
fixed4 num6 = saturate(numid_1 + numid_3 + numid_4 + numid_5 + numid_6 + numid_7);
fixed4 num7 = saturate(numid_1 + numid_2 + numid_3 + numid_6);
fixed4 num8 = saturate(numid_1 + numid_2 + numid_3 + numid_4 + numid_5 + numid_6 + numid_7);
fixed4 num9 = saturate(numid_1 + numid_2 + numid_3 + numid_4 + numid_6 + numid_7);
fixed4 num0 = saturate(numid_1 + numid_2 + numid_3 + numid_4 + numid_5 + numid_6);
col = num8;
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
ENDCG
}
}
}
完成
位置を調整してすべての数字を並べたものが初めに出した完成品です。適当に座標をいじってください。
画像を以下に再掲します。
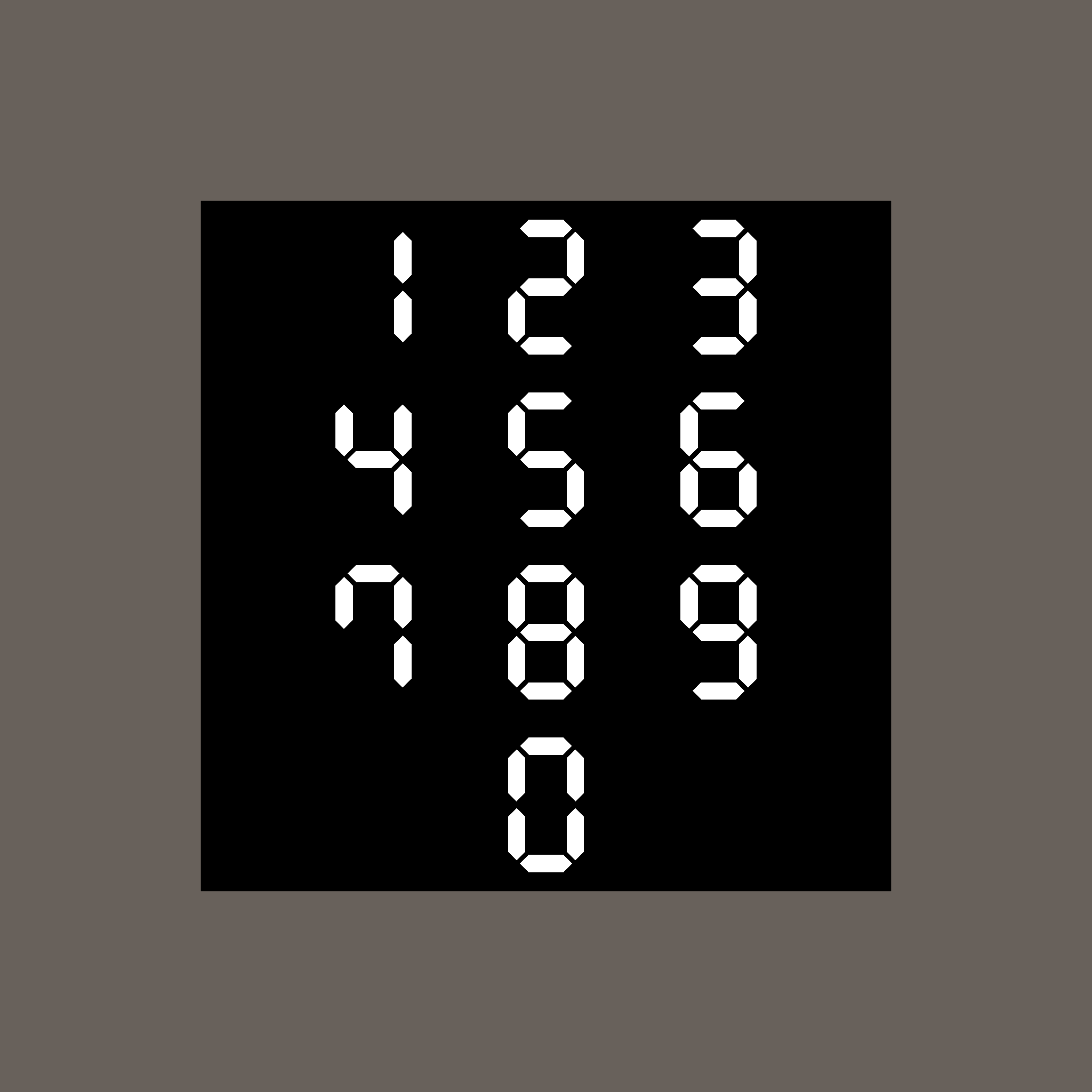
また、この状態のcolは数字部分のマスクカラーとしても利用可能です。
次の画像は完成品の数字部分にUV座標に対応する色を付けたものです。

下記のコードは、この完成品(色付き)を、それぞれのnumidとnumを関数にして記述したものです。
完成品色付きのコード(折り畳み)
Shader "Unlit/NumbersOrder"
{
Properties
{
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
// make fog work
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
};
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
UNITY_TRANSFER_FOG(o,o.vertex);
return o;
}
fixed hexa (float2 uv)
{
return step(-0.05, uv.y)*(1 - step(0.05, uv.y))*step(uv.y, uv.x + 0.15)*step(uv.y, -uv.x + 0.15)*(1 - step(uv.y, uv.x - 0.15))*(1 - step(uv.y, -uv.x - 0.15));
}
fixed4 numid_1(float2 uv)
{
fixed color = hexa(float2 (uv.x, uv.y - 0.34));
return fixed4 (color, color, color, 1);
}
fixed4 numid_2(float2 uv)
{
fixed color = hexa(float2 (uv.y - 0.17, uv.x - 0.17));
return fixed4 (color, color, color, 1);
}
fixed4 numid_3(float2 uv)
{
fixed color = hexa(float2 (uv.y + 0.17, uv.x - 0.17));
return fixed4 (color, color, color, 1);
}
fixed4 numid_4(float2 uv)
{
fixed color = hexa(float2 (uv.x, uv.y + 0.34));
return fixed4 (color, color, color, 1);
}
fixed4 numid_5(float2 uv)
{
fixed color = hexa(float2 (uv.y + 0.17, uv.x + 0.17));
return fixed4 (color, color, color, 1);
}
fixed4 numid_6(float2 uv)
{
fixed color = hexa(float2 (uv.y - 0.17, uv.x + 0.17));
return fixed4 (color, color, color, 1);
}
fixed4 numid_7(float2 uv)
{
fixed color = hexa(uv);
return fixed4 (color, color, color, 1);
}
fixed4 num1(float2 uv)
{
return saturate(numid_2(uv) + numid_3(uv));
}
fixed4 num2(float2 uv)
{
return saturate(numid_1(uv) + numid_2(uv) + numid_4(uv) + numid_5(uv) + numid_7(uv));
}
fixed4 num3(float2 uv)
{
return saturate(numid_1(uv) + numid_2(uv) + numid_3(uv) + numid_4(uv) + numid_7(uv));
}
fixed4 num4(float2 uv)
{
return saturate(numid_2(uv) + numid_3(uv) + numid_6(uv) + numid_7(uv));
}
fixed4 num5(float2 uv)
{
return saturate(numid_1(uv) + numid_3(uv) + numid_4(uv) + numid_6(uv) + numid_7(uv));
}
fixed4 num6(float2 uv)
{
return saturate(numid_1(uv) + numid_3(uv) + numid_4(uv) + numid_5(uv) + numid_6(uv) + numid_7(uv));
}
fixed4 num7(float2 uv)
{
return saturate(numid_1(uv) + numid_2(uv) + numid_3(uv) + numid_6(uv));
}
fixed4 num8(float2 uv)
{
return saturate(numid_1(uv) + numid_2(uv) + numid_3(uv) + numid_4(uv) + numid_5(uv) + numid_6(uv) + numid_7(uv));
}
fixed4 num9(float2 uv)
{
return saturate(numid_1(uv) + numid_2(uv) + numid_3(uv) + numid_4(uv) + numid_6(uv) + numid_7(uv));
}
fixed4 num0(float2 uv)
{
return saturate(numid_1(uv) + numid_2(uv) + numid_3(uv) + numid_4(uv) + numid_5(uv) + numid_6(uv));
}
fixed4 frag (v2f i) : SV_Target
{
fixed4 col = fixed4 (1, 1, 1, 1);
i.uv -= 0.5;
i.uv *= 4;
col = saturate(num1(float2(i.uv.x+1, i.uv.y-1.5)) + num2(float2(i.uv.x, i.uv.y-1.5)) + num3(float2(i.uv.x-1, i.uv.y-1.5)) + num4(float2(i.uv.x+1, i.uv.y-0.5)) + num5(float2(i.uv.x, i.uv.y-0.5)) + num6(float2(i.uv.x-1, i.uv.y-0.5)) + num7(float2(i.uv.x+1, i.uv.y+0.5)) + num8(float2(i.uv.x, i.uv.y+0.5)) + num9(float2(i.uv.x-1, i.uv.y+0.5)) + num0(float2(i.uv.x, i.uv.y+1.5)));
col.xy = (i.uv + 0.5)*col;
// apply fog
UNITY_APPLY_FOG(i.fogCoord, col);
return col;
}
ENDCG
}
}
}
余談
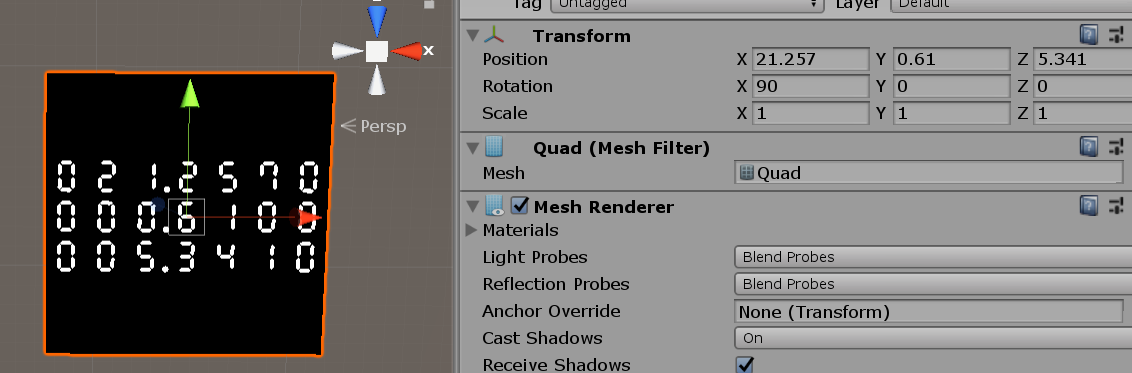
Shader内の数値に応じて表示する値を変えるようにすれば、カウンターのように扱うこともできます。
例えば次の画像写っているシェーダーは、オブジェクトのワールド座標を表示するようになっています。
編集後記
これシェーダーでやる必要ある?
利点としては、数式で描いているのでどれだけ拡大してもジャギーが出ません。代わりにパフォーマンスとコンパイルにかかる時間を犠牲にします。やりすぎには気を付けましょう。
とにもかくにも、これでシェーダーで図柄を描くことができるという事は分かったのではないでしょうか。肝は、描きたい図柄がどんな数式で表すことができるかを考えることと、描きやすい位置で描いて、座標をずらすことです。
今回は使いませんでしたが、円などを描く際には極座標変換も有用でしょう。
動きのある模様や色を描いたりするともっと楽しいかもしれません。
記事の内容は以上となります。
-
この記事内ではstepで指定する範囲を表す際にしばしば等号を省略しますのであしからず。
今回はこれを使ってUV座標がある特定の値の範囲内かどうかを判定し、それによって図形を描きます。 ↩ -
今回傾きは考えないので省略します
直線の下側の範囲は y < x - a です。
まず y < x と y > -x で切り分け、それから位置を調整していきます。
y < x の場合はstep(i.uv.y, i.uv.x)
y < -xの場合はstep(i.uv.y, -i.uv.x);です。
stepの第一引数に左辺が、第二引数に右辺が入っています。
長方形のときと同様乗算して、
step(i.uv.y, i.uv.x)*step(i.uv.y, -i.uv.x)とします。
colに乗算して ↩ -
以降この部分の説明は省略します
以下の記述を//ここで値を代入部分に記載します。 ↩



