 ## 石取りゲームとは
盤面に石がいくつか置かれており,プレーヤが石を取っていった後に勝ち負けが決まるようなものが石取りゲームです.石取りゲームには様々な種類がありますが,この記事では,
## 石取りゲームとは
盤面に石がいくつか置かれており,プレーヤが石を取っていった後に勝ち負けが決まるようなものが石取りゲームです.石取りゲームには様々な種類がありますが,この記事では,
- プレーヤーは2人
- 2人は交互に一つずつ石を取る
- それぞれの石には得点が書かれている
- 石を取りきった後の総得点を競う
というようなものを考えていきます.

石取りゲームの難しさは,両プレーヤーそれぞれが自分にとって最適な戦略を取ることです.自分一人で石を取るだけなら常に思い通りの(自分にとって最適な)盤面を作ることができますが,2人でゲームをすると相手も最適なプレーをするため,逆にそれは自分にとっては最悪な盤面になってしまいます.
大抵こういったゲームには各盤面で取るべき最適な戦略や必勝法が決まっていたりします.しかし,非常に複雑な盤面では必勝法がわからないこともありますし,そもそも必勝法がないこともあります.そんなときに,コンピュータの力で勝敗を導き出すのが本記事の目的です.ここではいくつかのゲームパターンにおいて,勝敗や得点を計算する方法を考えていきます.
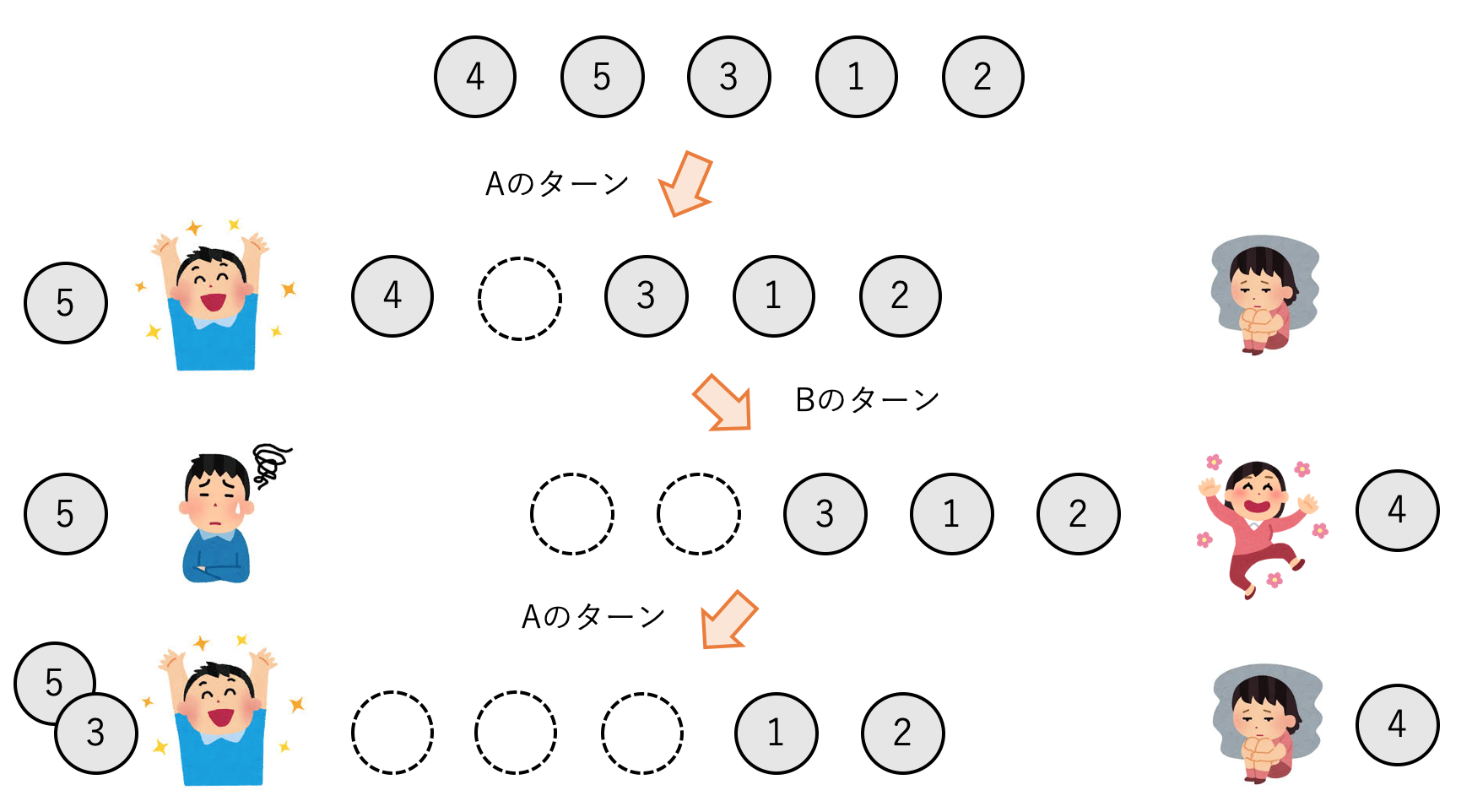
Game 1: 両端から取るゲーム(1)
石が一列に並べられており,それぞれの石には得点が書かれています.2人のプレーヤーは交互に石を取りますが,このとき列の両端にある石のどちらかしか取ることができません.石がなくなったら終わりです.2人のプレーヤーがそれぞれ常に最適な戦略を取るとき,どちらが勝つでしょうか?
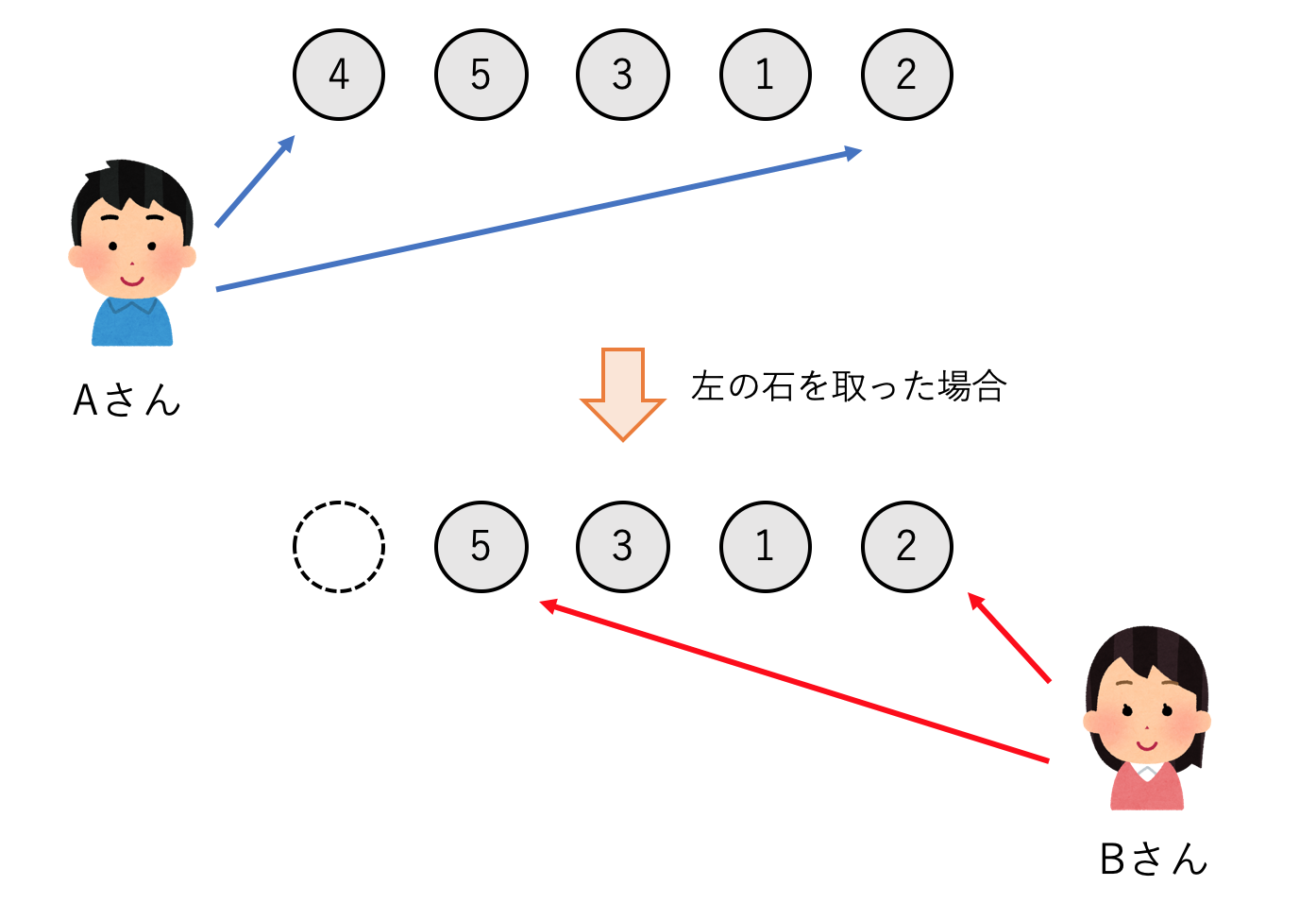
ここでは,一列に並んだ石の得点を配列で表現します.上の画像の例だと配列は
stones = [4,5,3,1,2]
のようになります.2人のプレーヤーのうち先攻をA,後攻をBとします.まずAは4の石を取るか2の石を取るか2種類の選択肢があります.4の石をとった方が得点は高くなりますが,次に相手に5の石を取られてしまいます.逆に2の石をとれば得点は少ないですが,次に相手が取れるようになるのは1の石です.また極端な例として,$stones = [1,100,2,3]$のような石列であれば,100の石を取れるかどうかが勝敗を決めるでしょう.
この問題を解くために,左右の石をそれぞれ取っていった全ての場合を全探索すればいいのでしょうか?それでは自分の得られる最大の利益を求めることはできるかもしれませんが,相手が最適な戦略をとっているとは限らないので,ゲームが成立していません.そう考えるとそもそも最適な戦略というものがなんなのかよくわからなくなります.
解法1
ここで,何かしらの最適な戦略があると仮定し,それを$strategy$とおいてしまいます.配列に対して$strategy$を適用すると,先攻の人が得られる得点が返ってくるとします.
max\_score = strategy(stones[:])
$strategy$の中では何が行われているのでしょうか.それは,右の石を取った時と左の石を取った時の得点を比較し,より得点が大きくなる方を選ぶような操作だと思われます.
max\_score = \max \left\{
\begin{array}{l}
stones[0] + strategy\_inv(stones[1:]) \\
stones[-1] + strategy\_inv(stones[:-1])
\end{array} \right.
ここで$strategy\_inv$は,プレーヤーBが残っている石に対して最適なプレイングをした際にAが得られる得点です.Bが自分の得点を最大化することとAの得点を最小化することは同じなので,Aからすると最悪な戦略を取られていることになります.具体的に$strategy\_inv$は,残っている石列のうち左右の石を取った場合に,よりAの得点が低くなる石を選ぶようなものです.
max\_score = \max \left\{
\begin{array}{l}
stones[0] + \min \left\{
\begin{array}{l}
stones[1] + strategy(stones[2:]) \\
stones[-1] + strategy(stones[1:-1])
\end{array} \right. \\
stones[-1] + \min \left\{
\begin{array}{l}
stones[0] + strategy(stones[1:-1]) \\
stones[-2] + strategy(stones[:-2])
\end{array} \right.
\end{array} \right.
$\min$,$\max$が出てきてややこしくなってきましたが,式の中に再び$strategy$が現れました.Bの前に石を取るのはAなので,この$strategy$は再びAの得点を最大化するようなものです.重要なのは,これが漸化式の形になっていることです.つまり,この$strategy$関数を定義して入れ子のように計算すれば,具体的な最適戦略を知らなくても計算を行なっていくことができます.
def stone_game(stones: List[int]) -> int:
n = len(stones)
def strategy(i, j):
if i > j:
return 0
if i == j:
return stones[i]
left = min(stones[i+1] + strategy(i+2, j), stones[j] + strategy(i+1, j-1)) # プレーヤーが左の石を取った時
right = min(stones[i] + strategy(i+1, j-1), stones[j-1] + strategy(i, j-2)) # プレーヤーが右の石を取った時
return max(stones[i] + left, stones[j] + right)
return strategy(0, n - 1) # Aの得られる総得点
コードでは部分配列を入力する代わりに配列の開始点と終了点のインデックス$i, j$を引数にしています.漸化式には初期値が必要ですが,残りの石が0個,1個になったような場合は最適戦略は明らかなのでそれは別に定義しています.最終的にAとBの得点を比べれば勝敗がわかります.
解法2
解法1によって最適戦略を毎回具体的に考えることなく問題を解くことができましたが,式がやや複雑なのが難点です.プレーヤーAとBは最適な戦略を取っているという点で同じなので,それをどうにかして統一できないでしょうか?
$strategy$の返り値を,Aの総得点ではなく,AとBの最大得点差ということにしてみます.
score\_dif = strategy(stones[:])
すると,解法1の式を以下のように変更できます.
score\_dif = \max \left\{
\begin{array}{l}
stones[0] - strategy(stones[1:]) \\
stones[-1] - strategy(stones[:-1])
\end{array} \right.
得点差なので足し算だった部分が引き算になります.そしてその結果,ここに$strategy\_inv$ではなく$strategy$が現れました.これで漸化式がだいぶ簡単になりました.
def stone_game(stones: List[int]) -> int:
n = len(stones)
def strategy(i, j):
if i > j:
return 0
return max(stones[i] - strategy(i+1, j), stones[j] - strategy(i, j-1))
return strategy(0, n - 1) # AとBの得点差
なお,$strategy$関数は入力する配列,つまり$i, j$が決まれば返り値は一つに定まります.計算の過程で,違うルートから同じ部分配列に達する場合も頻繁にあるはずなので,これを毎回計算するのは無駄です.よってここではメモ化再帰を行います.メモ化再帰は既に見た関数の入力と出力を記録しておくようなもので,同じ関数を何度も計算することを避け,大きな計算時間節約に繋がります.
メモ化再帰は辞書$dict$で値を保持するような方法もありますが,pythonでは関数の前に$@functools.lru\_cache()$をつけることでメモ化された関数にすることができます.
def stone_game(stones: List[int]) -> int:
n = len(stones)
@functools.lru_cache(None) # メモ化再帰
def strategy(i, j):
if i > j:
return 0
return max(stones[i] - strategy(i+1, j), stones[j] - strategy(i, j-1))
return strategy(0, n - 1)
この結果,各$i, j$の組み合わせに対して1度ずつだけ$strategy$の計算を行うことになりました.組み合わせの個数は$O(n^2)$,$strategy$内の計算量は$O(1)$なので,全体の時間計算量は$O(n^2)$となります.また空間計算量もメモ化によって$O(n^2)$となります.
勝敗を求める
解法2で勝敗を求めるときには,最終的な$score\_dif$が正なのか負なのかを見ます.得点差なので,$score\_dif$が0より大きければ先攻のAの勝ち,0より小さければBの勝ちになります.0なら引き分けです.
def stone_game(stones: List[int]) -> str:
def strategy(i, j):
# 中身は同じ
score = strategy(0, n - 1)
if score > 0:
return "A win"
elif score < 0:
return "B win"
else:
return "draw"
総得点を求める
一方Aの総得点を求める際は,$score\_dif$を利用して,
score\_A = \frac{\sum_{i=1}^n stones[i] + score\_dif}{2}
と計算できます.
def stone_game(stones: List[int]) -> int:
def strategy(i, j):
# 中身は同じ
return (sum(stones) + strategy(0, n - 1)) // 2
(おまけ)必勝になる場合
ちなみにコーディングとは無関係ですが,石の数が偶数の場合は先手必勝になる簡単な戦略があります.
偶数個の石を以下のように交互に2色に塗り分けます.
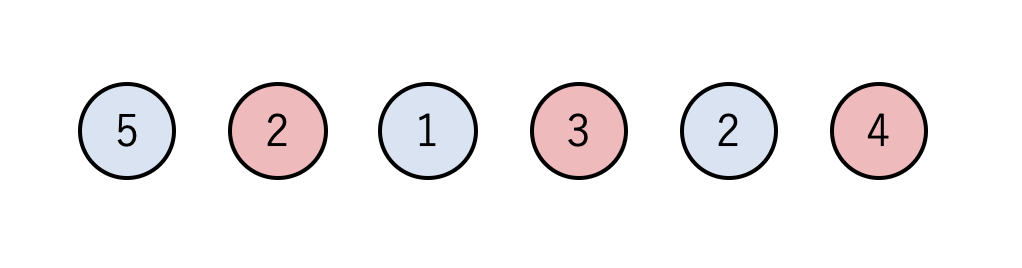
赤色と青色の石を足すと赤色の方が総和が大きいことがわかります.ここで,先手のAが右側にある赤色の石(4)を取ったとき,Bは次に青色の石(5か2)しか取ることができません.Bがどちらの石をとっても,Aは赤色の石を取ることができ,Bはまた青色の石しか取れません.このようにしてAが全ての赤い石を取れば,Aが必ず勝つ(少なくとも負けない)ようにできます.
Game 2: 両端から取るゲーム(2)
Game 1を少し変えて,**「石を取った時に,取った石ではなく残っている石の点の総和がもらえる」**というゲームも考えることができます.この場合はどうなるでしょうか?
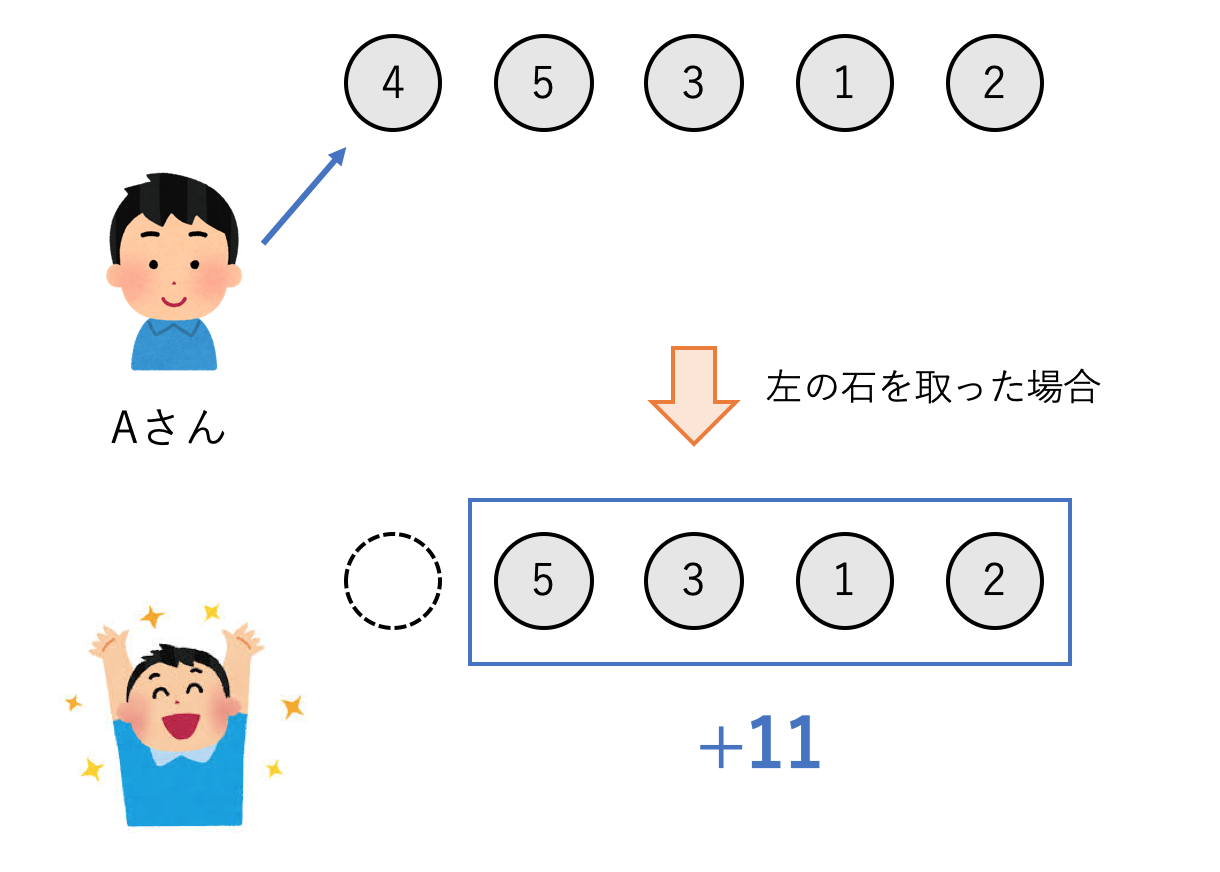
解法1
得られる得点が「取った石の点数」→「残りの石の点数の和」に変わるだけなので,Game 1の関数からその部分だけ変えれば良いです.例えば左の石を取った時の得点が
score = stones[i] - strategy(i+1, j)
だったものが
score = sum(stones[i+1:j]) - strategy(i+1, j)
になります.簡単ですね.
def stone_game(stones: List[int]) -> int:
n = len(stones)
@functools.lru_cache(None)
def strategy(i, j):
if i >= j:
return 0
left = sum(stones[i+1:j]) - strategy(i+1, j)
right = sum(stones[i:j-1]) - strategy(i, j-1)
return max(left, right)
return strategy(0, n-1)
解法2
しかし,解法1には致命的な欠点があります.部分配列の和を求める部分$sum(stones[i:j])$には$O(n)$の時間がかかるため,全体の計算量が$O(n^2)$になってしまうのです.これを防ぐため累積和を計算しておきます.累積和は先頭からの値の合計をあらかじめ配列として保持しておくことで,部分配列の和を$O(1)$で求めることができるものです.pythonでは,$itertools.accumulate()$関数が勝手に累積和を求めてくれます.これを$prefix\_sum$とおいて,改善されたコードは以下のようになります.
def stone_game(stones: List[int]) -> int:
n = len(stones)
prefix_sum = [0] + list(itertools.accumulate(stones)) # 累積和
@functools.lru_cache(None)
def strategy(i, j):
if i >= j:
return 0
left = (prefix_sum[j+1] - prefix_sum[i+1]) - strategy(i+1, j) # 左の石を取った場合
right = (prefix_sum[j] - prefix_sum[i]) - strategy(i, j-1) # 右の石を取った場合
return max(left, right)
return strategy(0, n-1)
これで計算量が$O(n)$になりました.
解法3
メモ化再帰以上に最適な解法があるわけではないのですが,別の書き方も紹介しておきます.メモ化再帰によって入れ子的に関数を呼び出すのではなく,得られた結果を配列に格納して適宜読み取ることを考えます.本質的にはメモ化再帰とやっていることは同じですが,こちらの方がいわゆる動的計画法のイメージに近い方法です.
ここでは縦横の長さ$n$の2次元配列$dp$を用意します.$dp[i][j]$には解法2における$strategy(i, j)$の出力が入ることになります.コードの上ではほぼ解法2の$strategy(i, j)$が$dp[i][j]$に変わるだけです.しかし,$dp$を計算する順序には注意する必要があります.$dp[i][j]$を計算する際にはその内側にあるインデックス$a, b~(i <= a <= b <= j)$に対して$dp[a][b]$が求まっていなければなりません.よって,$dif$を$i$から$j$の差として,$dif$が小さい方から順に$dp[i][j]$を計算していきます(これはいわゆる「区間DP」という方法です).
def stone_game(stones: List[int]) -> int:
n = len(stones)
prefix_sum = [0] + list(itertools.accumulate(stones))
dp = [[0]*n for _ in range(n)] # 値を格納する配列
for dif in range(1, n): # 求める配列の幅, 順に長くしていく
for i in range(n-dif): # 配列の開始地点
j = i+dif # 配列の終了地点
left = (prefix_sum[j+1] - prefix_sum[i+1]) - dp[i+1][j]
right = (prefix_sum[j] - prefix_sum[i]) - dp[i][j-1]
dp[i][j] = max(left, right)
return dp[0][n-1]
解法2と3の理論的な計算量は同じですが,実際は解法3の方がたいてい計算時間は速くなります.解法2で遅すぎる場合は3で書き直すとうまくいったりします.
区間DPを使ったGame 1の解法
ちなみにGame 1も区間DPを使えば解法3のように解くことができます.
def stone_game(stones: List[int]) -> int:
n = len(stones)
dp = [[0]*n for _ in range(n)]
for dif in range(1, n):
for i in range(n-dif):
j = i + dif
dp[i][j] = max(stones[i] - dp[i+1][j], stones[j] - dp[i][j-1])
return dp[0][n-1]
Game 3: 端から順に取るゲーム(1)
続いては,両端から石を取るのではなく,一方の端からのみ順に石を取っていく設定を考えます.ただ,1個ずつ石を取っていては何のゲーム性もないので,一回に取れる石の数を1,2,3個いずれかから選択できるとします.今回も石を最後まで取りきった時総得点が高い方が勝ちです.
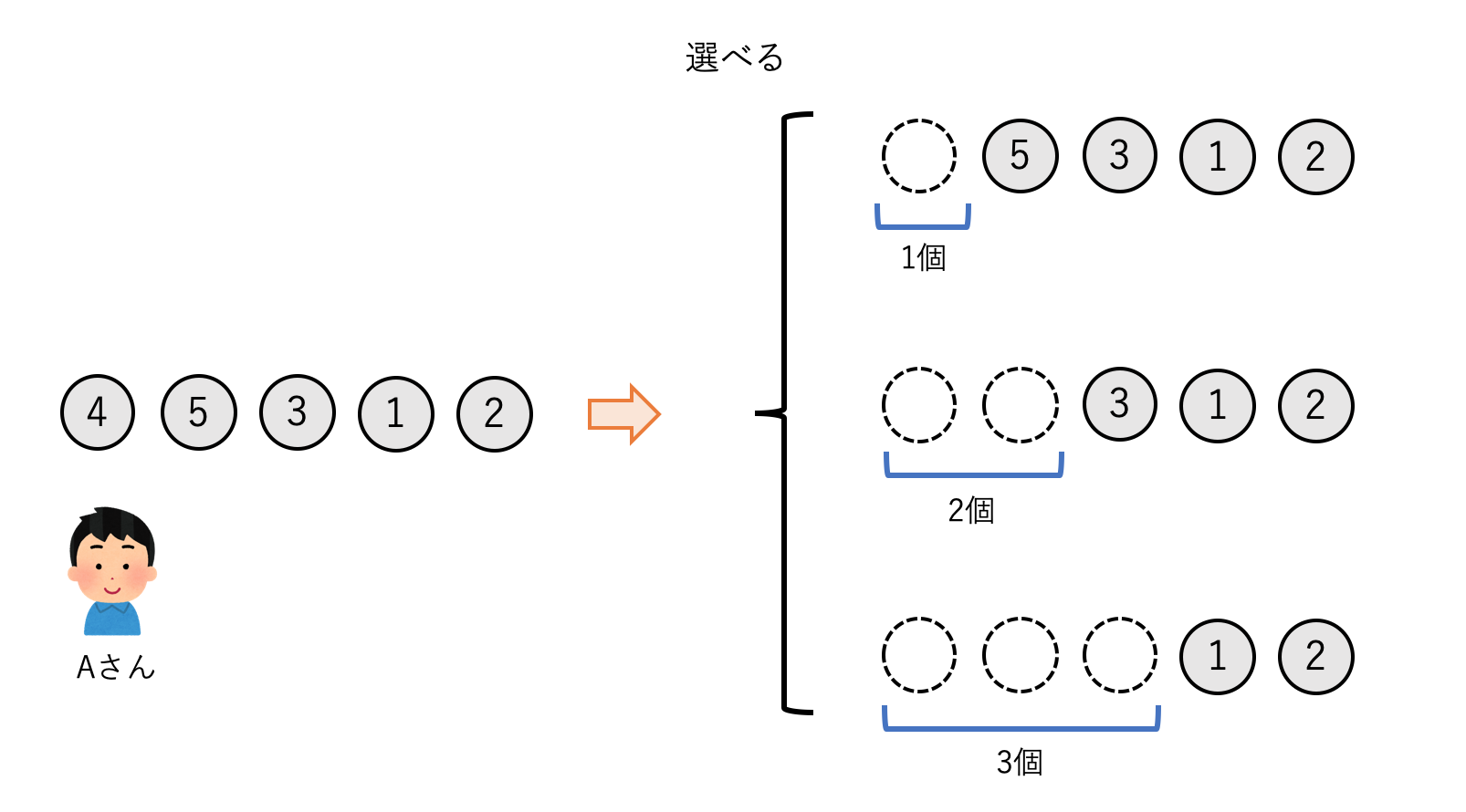
解法1
Game 1やGame 2の解説から.部分配列を入力,得点差を出力とし,最適戦略を再帰的に表現する$strategy$関数を構築することで問題を解けることがわかりました.その戦略をこのゲームに対しても適用します.
この場合$strategy$関数は,取る石の数が1~3個の場合に得られる最大得点差をそれぞれ計算し,それらの最大値を返すようなものになります.
score\_dif = \max \left\{
\begin{array}{l}
stones[0] - strategy(stones[1:]) \\
stones[0] + stones[1] - strategy(stones[2:]) \\
stones[0] + stones[1] + stones[2] - strategy(stones[3:])
\end{array} \right.
これを初期値や境界条件に注意しながら,Game 1と同じようにメモ化再帰で書くだけです.
def stone_game(stones: List[int]) -> int:
n = len(stones)
@functools.lru_cache(None)
def strategy(i):
if i >= n-1:
return sum(stones[i:])
return max(sum(stones[i:i + k]) - strategy(i + k) for k in (1, 2, 3)) # sumとfor文を使ってまとめた
return strategy(0)
今回は関数の引数が1つのインデックスだけなので,時間計算量,空間計算量は$O(n)$で済みます.
解法2
Game 2で見たように,配列に計算結果を格納する方法での解法も見ておきます.ここでは長さ$n$の1次元配列$dp$を用意し,$dp[i]$には$strategy(i)$の出力が入ります.今回はインデックスが1つしかないのでGame 2よりシンプルですが,計算する順序にはやはり注意する必要があります.$dp[i]$を計算する際にはより大きなインデックス$i < j$での$dp[j]$が求まっていなければなりません.よって,インデックスの大きい方から$dp[i]$を計算していきます.
def stone_game(stones: List[int]) -> int:
n = len(stones)
dp = [0] * (n+3) # インデックスエラーを防ぐため配列を長めに用意しておく
for i in reversed(range(n)): # i = n-1 ~ 0 の順でループ
dp[i] = max(sum(stones[i:i + k]) - dp[i + k] for k in (1, 2, 3))
return dp[0]
こちらも理論的な計算量は同じですが,実際には解法2の方が計算時間は速くなると思います.
Game 4: 端から順に取るゲーム(2)
ここで少しゲームルールを変えて,「プレーヤーはこれまで取られた石の最大個数の2倍を超えない数の石を取ることができる」としてみます.つまり,これまでに最大で$M$個の石が取られた時,次のプレーヤーは$1 \leq X \leq 2M$を満たす$X$個の石を取ることができ,この範囲であれば好きな$X$を選択できます.さらにその次のプレーヤーに対しては$M = max(X, M)$となります.なお,はじめは$M=1$からスタートするものとします.
ここまでの内容を理解された方は,このような複雑な問題を見てももう解法がイメージできるのではないでしょうか?$strategy$の状態は,開始するインデックスと取れる石の最大個数$2M$によって決まります.コードは以下のようになります.
def stone_game(stones: List[int]) -> int:
n = len(stones)
@functools.lru_cache(None)
def strategy(i, M):
if i + 2 * M >= n:
return sum(stones[i:])
return max(sum(stones[i:i + X]) - strategy(i + X, max(M, X)) for X in range(1, 2 * M + 1))
return strategy(0, 1) # 初めはX = 1, M = 1
関数の入力と更新式が変わりましたが,やっていることはGame 3とほぼ同じです.
Game 5: 石の価値が違う場合のゲーム
最後に,また違ったルールのゲームを考えてみます.大きなルール変更は次の2つです.
- 場にある石のどれでも取っていい.
- 石の価値は2人のプレーヤーで異なる
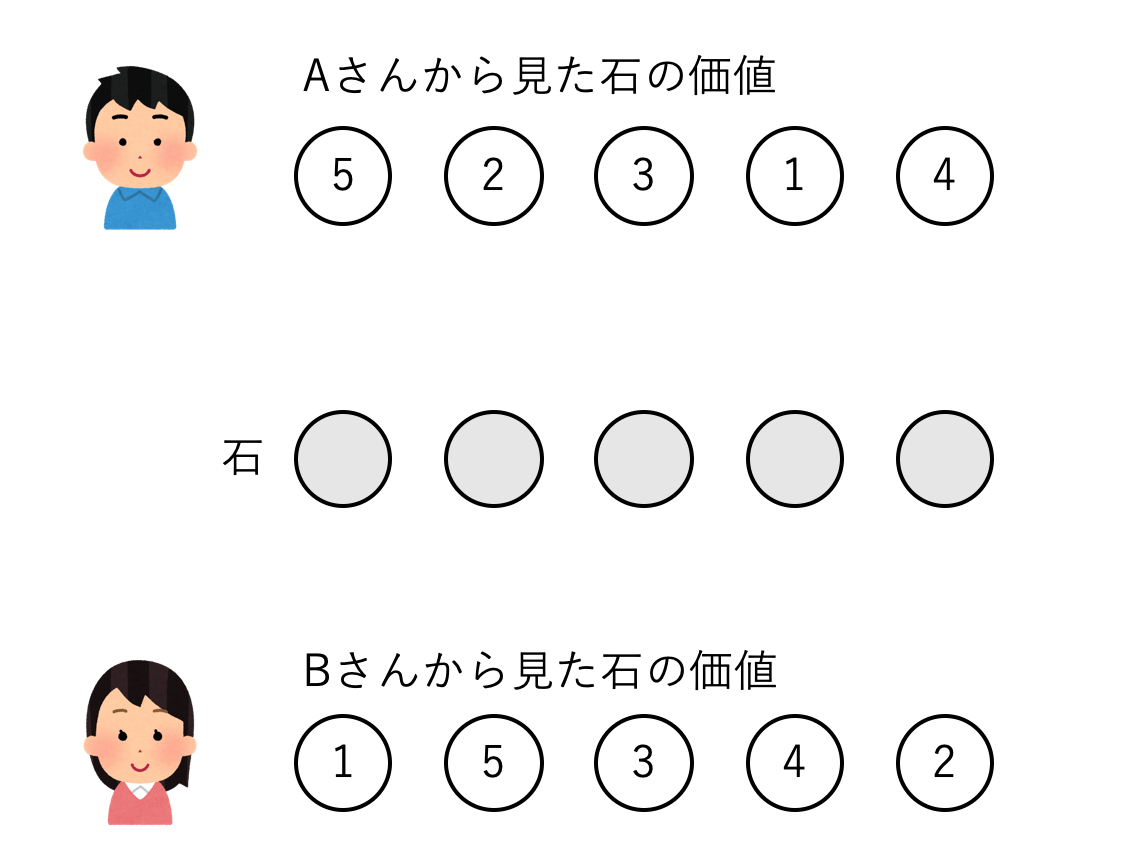
例えば場に石が5個あった時,Aから見た石の価値は順に5,2,3,1,4であり,Bから見た石の価値は順に1,5,3,4,2というように,同じ石でも両者の得られる得点が異なります.なお,両プレーヤーは相手の得点配分も見えているものとします.例えばAは1つ目の石(5点)を取れば最も得られる得点は高いですが,そうすれば次にBは2番目の石を取って5点を得るはずなので,先に2番目の石(2点)を取っておくべきかもしれません.
解法1
ただ我々は既に,得点差を出力とし最適戦略を再帰的に表現する$strategy$関数を構築することで問題を解けることを知っています.今回は列のどの位置から石を取ってもいいので,既に残っている石と取られた石の場所を表す$state$配列を導入します.$i$番目の石が既に取られていれば$state[i] = False$,残っていれば$True$とします.プレーヤー名と$state$を入力として,まだ残っている石をそれぞれ取った時の得点を求め,最大得点を返す関数を書きます.
def stone_game(values_A: List[int], values_B: List[int]) -> int:
n = len(values_A)
state = [True]*n
@lru_cache(None)
def strategy(player, state):
if max(state) == 0: # 全てFalse, つまり全ての石が取られているなら0を返す
return 0
max_value = float("-inf")
state = list(state)
for i in range(n):
if state[i]: # もし石iが残っていれば
state[i] = False # 石iを取ったことにする
if player == "A": # プレーヤーAとBで場合分け
max_value = max(max_value, values_A[i] - strategy("B", tuple(state)))
else:
max_value = max(max_value, values_B[i] - strategy("A", tuple(state)))
state[i] = True # 石iを取られていない状態に戻す
return max_value
return strategy("A", tuple(state)) # 先攻はA, stateは全てTrue
なお,pythonにおいて配列はhashableではなくメモ化できないので,$state$を関数に入力する際はtupleに変換しています.これで各$state$に対して得られる得点が求まり,計算できるようになりました.
しかしこれで本当にいいのでしょうか?今までは配列の両端からしか石を取らなかったものが,どこからでも石を取ってもよくなったことで,$state$のバリエーションは膨大になっています.具体的には$n$個それぞれの地点が$True$か$False$を取れるため,組み合わせの個数のオーダーは$O(2^n)$になってしまいます.これではせいぜい$n=30$くらいまでしか気軽に計算できないでしょう.
解法2
実はこのゲーム,はるかに簡単に計算できます.まず問題を単純化して,石の価値が両者で同じ場合を考えてみます.この場合,再帰をするまでもなく,一番得点の高い石から順に取っていくのが最適です.これは直感的には以下の2つの理由によるものです.
- 得点の大きい石を取れば自分の得点を大きくできる.
- 得点の大きい石を取れば相手はその石を取れず,相手の得点を減らせる.
これが,両者の石の価値が違う場合にも成り立ちます.一つの石を取った場合に生まれる相手との得点差は,(自分が得た得点)+(その石がなくなったことで相手が得られなくなった得点)と考えることができます.それはつまり,自分から見た石の得点と相手から見た得点の和です.得点差を大きくするためには結局,両者にとっての価値を石ごとに足して,価値の大きい石から順に取っていくのが最適になります.
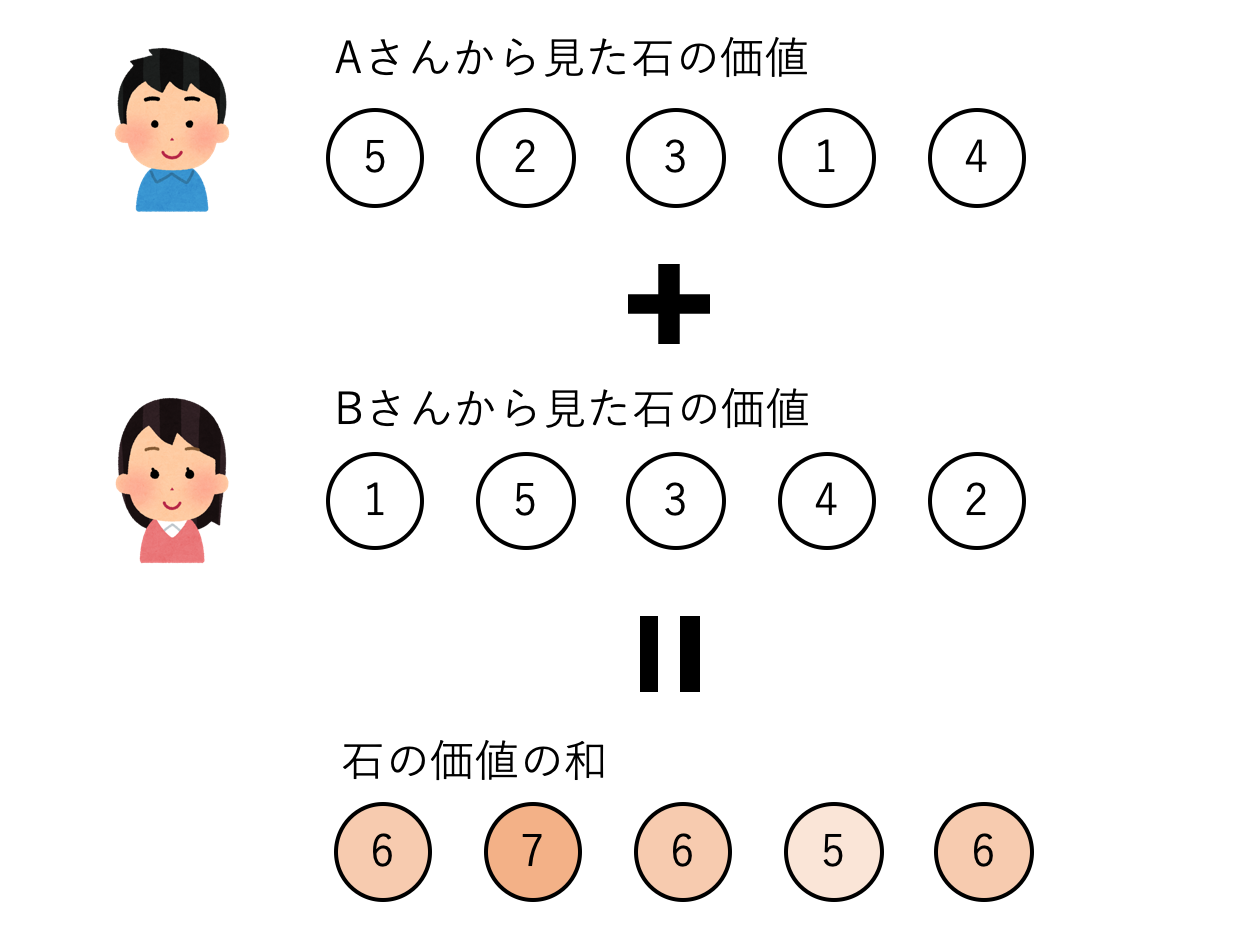
def stone_game(values_A: List[int], values_B: List[int]) -> int:
sorted_sum_value = sorted(zip(values_A, values_B), key=sum, reverse=True) # 石ごとの価値の和を降順に並べている
sum_A = sum(a for a, b in sorted_sum_value[::2]) # 先頭の石から一つおきに取れる
sum_B = sum(b for a, b in sorted_sum_value[1::2]) # 2個目の石から一つおきに取れる
return sum_A - sum_B
これなら計算量は$O(n)$になりました.この問題に関しては定石メソッドを適応するよりさらに良い方法があるということで,石取りゲームの奥深さが感じられます.
まとめ
ここまで,得点の異なるいくつかの石があり,2人でその石を取り合う場合に,どちらがより多くの得点を取れるのか,また何点取れるのかという問題を考えてきました.ポイントは,
- 各状態を単純な形(インデックスなど)で表す
- 各状態を入力,得られる得点(の差)を出力とし,最適な行動をとる関数を再帰的に書く
- メモ化やDPによって計算量を減らす
でした.今後もし他人から石取りゲームを申し込まれた場合は,確実に勝てるか見極めてから応じるようにしましょう.
参考(Leetcodeより)
Stone Game
Stone Game VII
Stone Game III
Stone Game II
Stone Game VI