実世界での株取引では,刻一刻と変化する株の値を見ながら,新たな株を買ったり自分の所有する株を売ったりしてより多くの利益を得ることを目指します.
もちろん株の値動きを予測するのはとても難しく,この記事もそれを目指している訳ではありません.実際の状況では未来の値動きはわからないのですが,今回はこれを単純化し,値動きを記録した数値の列が与えられたときに,いつ「売り」や「買い」を行えば最も高い利益を得られるかを考えます.
問題設定
これは,各時刻での株価が入った配列を入力として,そこから得られる最大利益を出力するような関数を設計する問題になります.
def calculate_max_profit(prices: List[int]) -> int:
...
return max_profit
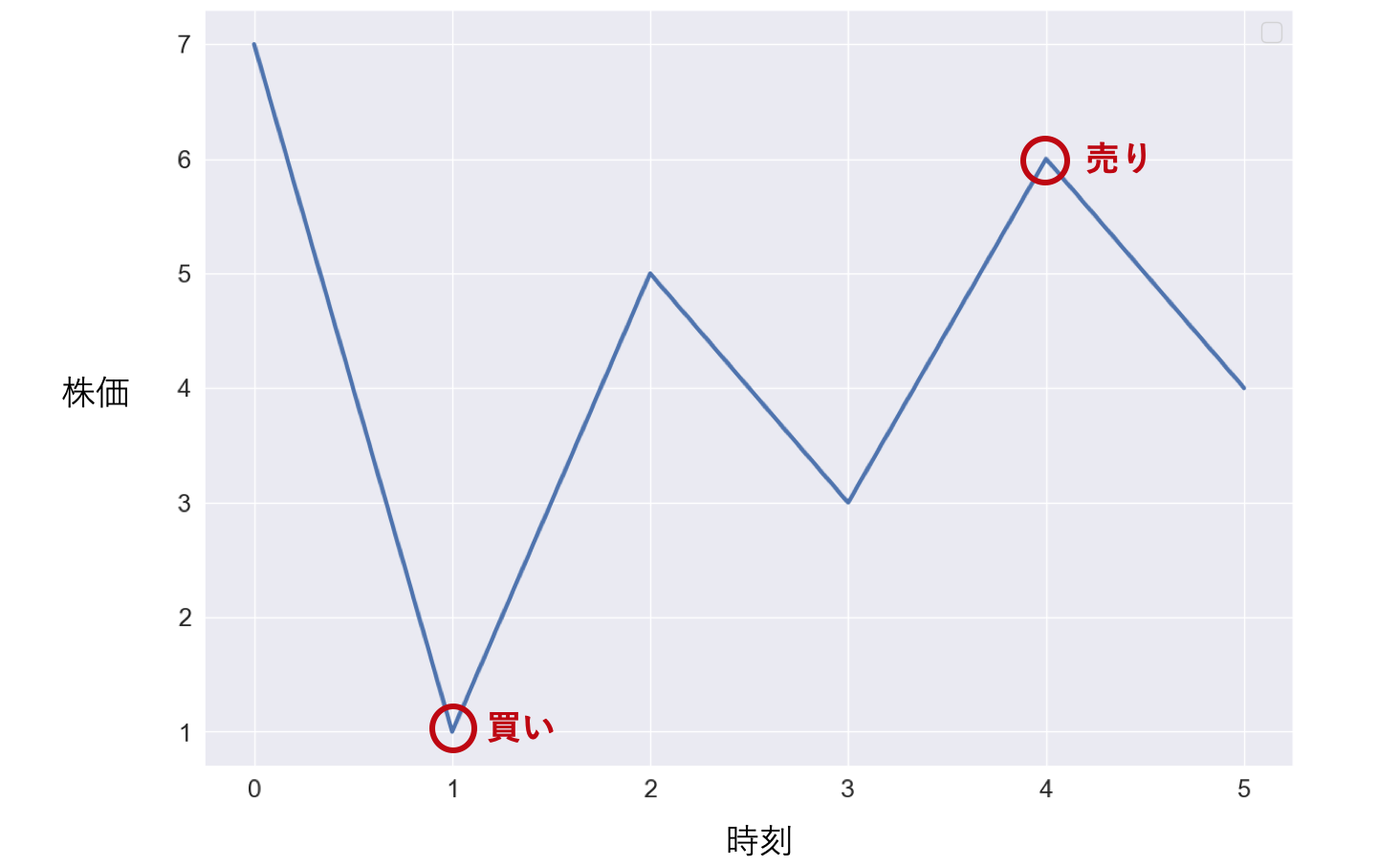
例えば上のグラフだと入力は
prices = [7,1,5,3,6,4]
のようになります.基本的なルールは以下のようなものです.
- 各時刻で買う操作と売る操作のどちらかを行うことができる(何もしなくても良いが両方同時刻にはできない).
- 買う前に売ることはできない
- 買う操作と売る操作は交互にしなければならない(買う→売る→買う→売る...としなければいけない).
- ある時刻に株を買えばその時刻での株価が持ち金から引かれ,ある時刻に株を売ればその時刻での株価分のお金を得ることができる.
- 最初の持ち金は0.持ち金は0以下になってもよい.
- 最終的な持ち金の額を最大化したい.
あらかじめ各時刻の値段がわかっていればすぐ計算できそう感じもしますが,問題が複雑になればそう簡単にはいきません.条件の違いによって様々なパターンがあるので,この記事ではそれを一挙に紹介します.
Case 1: 1回だけ売り買いできる場合
まず,最も基本的な場合として,買う操作と売る操作を1度ずつしかできない場合を考えます.例えば,$prices = [7,1,5,3,6,4]$の場合は,最初の図に書いたように時刻$t=1$で買い,時刻$t=4$で売ることで最大利益5を得ることができます(最初を$t=0$としています).ルール上,先に$t=0$で売って$t=1$で買うことで利益6を得る,というようなことはできません.一方,もし$prices = [7,6,4,3,1]$であれば,一度も売り買いをしない場合に利益が0で最大になることがわかります.
最も基本的な解き方は,買う時刻と売る時刻を全探索することです.
def calculate_max_profit(prices: List[int]) -> int:
n = len(prices)
max_profit = 0
for i in range(n): # 買う時刻
for j in range(i+1, n): # 売る時刻
max_profit = max(max_profit, prices[j] - prices[i]) # 最大利益を更新
return max_profit
この方法では,$prices$の長さを$n$として$O(n^2)$の時間計算量となります.
ここから時間計算量を抑える方法を考えます.まず,ある時点$t = i$で株を売ることを考えます.ここで売ることを決めている場合,いつ株を買っていることが望ましいでしょうか?それは$t = i$より前で最も株価が安い時です.つまり,$t = i$以前での株価の最小値がわかっていれば,その差が得られる利益の最大値となるのです.ということは$prices$を走査する間,最小値さえ保持していれば計算することができます.

def calculate_max_profit(prices: List[int]) -> int:
n = len(prices)
min_value = float("inf")
max_profit = 0
for i in range(n): # iは売る時刻
max_profit = max(max_profit, prices[i] - min_value)
min_value = min(min_value, prices[i]) # 最小値を更新
return max_profit
これで時間計算量は$O(n)$,空間計算量は$O(1)$に抑えられます.また,各時点での利益が0以下になる場合は$max\_profit = 0$となり,売り買いをしないほうがいいという結果が得られます.
Case 2: 2回まで売り買いできる場合
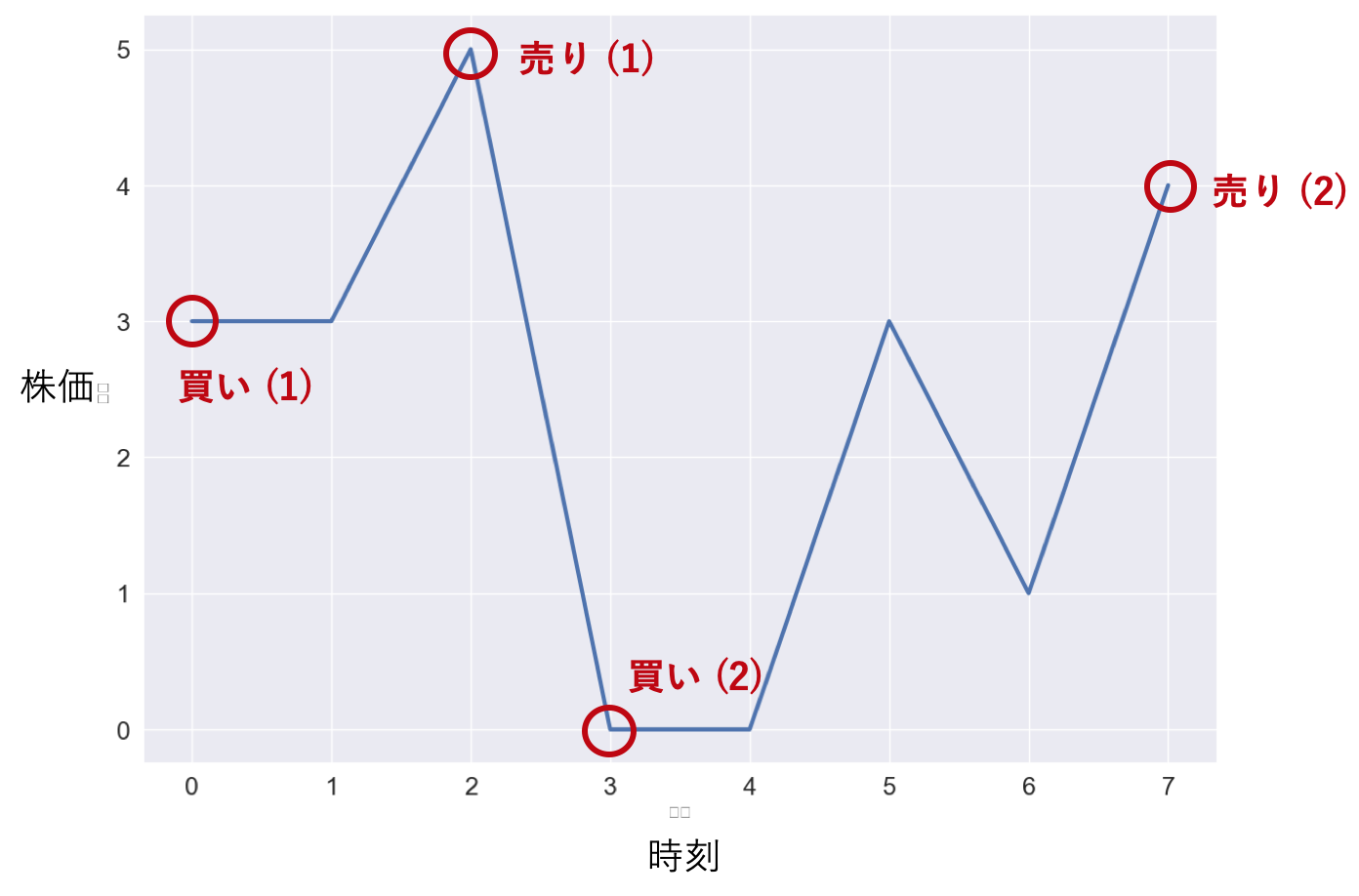
次は,売り買いできる回数を2回ずつまでという条件に変えてみます.$prices$の中で「買→売→買→売」を行うことができます.例えば,
prices = [3,3,5,0,0,3,1,4]
に対しては,$t=0$で買(-3)→$t=2$で売(+5)→$t=3$で買(-0)→$t=7$で売(+4),の手順で最大利益6を得ることができます.
1回のみの取引に対して複雑さが増しました.最も単純な計算方法はやはりそれぞれの操作のタイミングを全探索することですが,計算量は$O(n^4)$となり現実的ではありません.
ここで,ある時点$t=i$で1度目の「売り」を行うことを考えます.この売りに対して1度目の「買い」をいつ行えば良いのかはCase 1と同じ方法で求めることができます.では,これ以降2回目の売り買いの最大利益はどのように計算できるでしょうか?それは,$prices$の$t=i+1$以降の部分に対してもう一度同じ操作をしてやればいいのです.

擬似的には以下のようなコードになるでしょう.
def calculate_max_profit_twice(prices: List[int]) -> int:
min_value = float("inf")
max_profit = 0
for i in range(n):
current_profit = (prices[i] - min_value) + calculate_max_profit_once(prices[i+1:])
max_profit = max(max_profit, current_profit)
min_value = min(min_value, prices[i])
return max_profit
$calculate\_max\_profit\_once()$関数はCase 1の関数だと考えてください.この場合計算量は$O(n^2)$まで抑えることができました.
しかしまだ無駄な操作があります.$calculate\_max\_profit\_once()$は毎回同じような計算をしているのです.例えば,$t = i$以降の最大利益の計算と$t = i+1$以降の最大利益の計算はほとんど同じような操作を行なっているはずです.
この部分の無駄な計算を削減するために,ある時点$t = j$で2回目の株の「買い」を行うことに決めた場合を考えます.すると,この株を売るタイミングはいつが最適でしょうか?もちろん$t = j$以降で株が最も高くなる時刻です.これはCase 1と逆の状況と言えます.つまり,$t = j$以降の最大値を記録しておくことで,$t = j$での株を買うときの最大利益が求まります.

よって具体的には,はじめに各$j$以降で行われる2回目の取引の最大利益を配列$second\_trans\_max$に保存しておきます.その後$t = i$における1回目の取引の最大値をCase 1のように求め,$second\_trans\_max[i+1]$を加算することで,2回分の最大利益を求めることができるのです.
def calculate_max_profit(prices: List[int]) -> int:
n = len(prices)
if n < 2:
return 0
# 2回目の取引の最大利益を先に計算
second_trans_max = [0]*(n+1)
max_after = float("-inf")
for i in reversed(range(n)):
second_trans_max[i] = max(max_after - prices[i], second_trans_max[i+1]) # 2回目の取引の最大利益
max_after = max(max_after, prices[i]) # これ以降の最大値の更新
# 1回目の取引の最大利益を計算
max_profit = first_trans_max = 0
min_before = prices[0]
for i in range(1, n):
first_trans_max = max(prices[i]-min_before, first_trans_max) # 1回目の取引の最大利益
max_profit = max(first_trans_max + second_trans_max[i+1], max_profit) # 全体の最大利益
min_before = min(min_before, prices[i]) # これ以前の最小値の更新
return max_profit
なお,このコードには取引回数が0回,1回の場合も包含されています.これによって時間計算量は$O(n)$に減らすことができました.一方$second\_trans\_max$を保持する分,空間計算量は$O(n)$となります.
Case 3: 何回でも売り買いできる場合
続いて,何度でも制限なく売り買いができる場合を考えます.回数制限がなくなった分あらゆる可能性を考える必要が出てきて,問題がより複雑になったように感じますが,実はこの設定は難しくはありません.値が下がりそうになったらその前に売り,値が上がりそうになったら一番安い時に買う,という操作を繰り返すだけで良いのです.

def calculate_max_profit(prices: List[int]) -> int:
n = len(prices)
valley = peak = prices[0]
max_profit = 0
idx = 0
while idx < n-1:
while idx < n-1 and prices[idx] >= prices[idx+1]:
idx += 1
valley = prices[idx]
while idx < n-1 and prices[idx] <= prices[idx+1]:
idx += 1
peak = prices[idx]
max_profit += peak - valley
return max_profit
このコードは要するに値動きの頂上と谷底を探して記録しているだけです.これは直感的にも妥当な戦略ですが,次のように考えることもできます.例えば,$t = i$で株を買い,$t = j$で株を売るとします.もし,$i$から$j$までの間で(広義の)単調増加ではなく$prices[a] > prices[b] ~~(a < b)$となっていた時,$t=a$で売り,$t=b$で買いの操作を入れたほうがより利益を大きくすることができます.つまり,増減が入れ替わる点で常に売り買いを行うべきということになります.

なお,これは結局,「隣の株価が現時刻より大きければ利益に加算し,小さければ加算しない」という計算を行なっているのと同じです.これを凝縮すると解答を1行で書くこともできます.
def calculate_max_profit(prices: List[int]) -> int:
return sum([max(a-b, 0) for a, b in zip(prices[1:], prices[:-1])]) if prices else 0
ここでは増加分のみを足し合わせるために,隣接する値の差を取っています.いずれのコードも時間計算量は$O(n)$,空間計算量は$O(1)$となります.
Case 4: k回まで売り買いできる場合
続いてはいよいよこの記事の山場,売り買いの回数の上限が$k$回と決まっている場合です.これはCase 1やCase 2の一般形と言えます.ただし,$k$が3,4,5...となっていった場合,Case 1や2と同じように計算することはできません.またCase 3のようにただ増減のみを見て決定することができません.
ここで,解法を考える前にまず整理しておきたいのは,$k$が大きい時です.極端な話,$n = 10, k = 100$だった場合,実質的にこれは制限なく取引できるCase 3と同じ状況です.Case 3とCase 4の境界線はどこでしょうか?それは$k = \frac{n}{2}$の時です.長さ$n$の中で取引できる最大回数は$\frac{n}{2}$回なので,$k$がそれより大きい場合はCase 3を解けば十分です.

それでは$k$がそこまで大きくない場合について改めて考えていきます.例えば,ある$t = i$において,$t = i$までに$j$回目の「売り」を終えた後の最大利益$max\_sell[i][j]$,$j$回目の「買い」を終えた後の最大利益$max\_buy[i][j]$がそれぞれの$j$についてわかっているとします.すると$t = i+1$における$max\_sell$や$max\_buy$は以下のように計算できます.
\begin{align}
max\_buy[i+1][j] &= \max(max\_buy[i][j], max\_sell[i][j-1] - prices[i+1]) \\
max\_sell[i+1][j] &= \max(max\_sell[i][j], max\_buy[i][j] + prices[i+1])
\end{align}
これは一体どういうことでしょうか?まず$max\_buy$について,$j$回目の「買い」はルール上$j-1$回目の「売り」の後に行われます.よって,$i$地点での$j-1$回目の「売り」が終わった段階での最大利益$max\_sell[i][j-1]$から,$i+1$地点での$j$回目の「買い」にかかった費用$prices[i+1]$を引きます.これを$i$地点の$j$回目の「買い」が終わった時点での最大利益$max\_buy[i][j]$と比較しているのです.同様に,$max\_sell$について,$j$回目の「売り」は$j$回目の「買い」の後に行われるので,$i$地点での$j$回目の「買い」が終わった段階での最大利益$max\_buy[i][j]$に,$i+1$地点での$j$回目の「売り」で得た利益$prices[i+1]$を足します.これを$i$地点の$j$回目の「売り」が終わった時点での最大利益$max\_sell[i][j]$と比較しています.

これはまさしく$i$と$j$に関する動的計画法(DP)です.初期値と漸化式を適切に設定すれば,あらゆる$i$と$j$に関する値を効率的に計算できます.
def calculate_max_profit(prices: List[int], k: int) -> int:
n = len(prices)
if k == 0:
return 0
if k >= n//2:
# Case 3の場合
max_profit = 0
for i in range(1, n):
max_profit += max(0, prices[i] - prices[i-1])
return max_profit
else:
# 初期化
max_buy = [[float("-inf")]*(k+1) for _ in range(n)]
max_sell = [[float("-inf")]*(k+1) for _ in range(n)]
for i in range(n):
max_sell[i][0] = max_sell[i][0] = 0
max_buy[0][1] = -prices[0]
# DP
for i in range(1,n):
for j in range(k):
max_sell[i][j+1] = max(max_sell[i-1][j+1], max_buy[i-1][j+1]+prices[i])
max_buy[i][j+1] = max(max_buy[i-1][j+1], max_sell[i-1][j]-prices[i])
# 全jのうちの最大利益を返す
return max(max_sell[n-1])
これの時間計算量,空間計算量はともに$O(nk)$です.また計算の順序をうまく考えることで,DPの際に使うメモリを削減することができます.
def calculate_max_profit(prices: List[int]) -> int:
## これ以前は上と同じ
else:
# 初期化
max_buy = [float("-inf")]*(k+1)
max_sell = [float("-inf")]*(k+1)
max_sell[0] = 0
for i in range(n):
for j in reversed(range(k)):
max_sell[j+1] = max(max_sell[j+1], max_buy[j+1] + prices[i])
max_buy[j+1] = max(max_buy[j+1], max_sell[j] - prices[i])
return max(max_sell)
やっていること自体はどちらも同じですが,$max\_sell$と$max\_buy$を上書きすることで空間計算量を$O(k)$にできました.
※DPによる他の問題の解法
さて,この解法では「$i$地点で($k$回目の)「売り」「買い」をした後それぞれの状態での最大利益」を記録することで問題を解いています.この考え方を使ってこれまでの問題を解いてみます.Case 2に関しては,Case 4で$k = 2$になった特殊なケースなので,同じようにして解くことができます.
def calculate_max_profit(prices: List[int]) -> int:
n = len(prices)
max_buy1 = max_buy2 = float("-inf")
max_sell1 = max_sell2 = 0
for i in range(n):
max_sell2 = max(max_sell2, max_buy2 + prices[i])
max_buy2 = max(max_buy2, max_sell1 - prices[i])
max_sell1 = max(max_sell1, max_buy1 + prices[i])
max_buy1 = max(max_buy1, -prices[i])
return max(sell1, sell2)
変数が4個で済み,空間計算量は$O(1)$になりました.また,Case 3も以下のように解くことができます.
def calculate_max_profit(prices: List[int]) -> int:
max_sell, max_buy = 0, float("-inf")
for i in range(n):
sell, buy = max(sell, buy+prices[i]), max(buy, sell-prices[i])
return max_sell
何回でも取引が可能なため回数$k$を考える必要がなくなり,$sell$と$buy$を同時に計算しています.
Case 5: 売り買いに料金がかかる場合
Case 4がこの記事のメインテーマだったのですが,それ以外のやや変化球の設定を2つほど紹介します.1つ目は「1回の取引(売り買い)に手数料がかかる」場合です.このケースでは何回でも自由に取引が可能としますが,得られる利益が少額だと手数料によって逆に損失が発生してしまいます.どのように考えれば良いのでしょうか?
実はこれは簡単で,Case 3において$max\_sell$を更新する際に$fee$を引くだけです.$max\_buy + prices[i] - fee$の大小に応じて取引を行うかを決めれば良いのです.
def calculate_max_profit(prices: List[int], fee: int) -> int:
n = len(prices)
max_sell, max_buy = 0, float("-inf")
for i in range(n):
max_sell, max_buy = max(max_sell, max_buy + prices[i] - fee), max(max_buy, max_sell - prices[i])
return max_sell
Case 6: 連続では売り買いできない場合
最後に,「株を売ってから次買うまでに少なくとも一回分の間を入れないといけない」という条件を考えてみます.
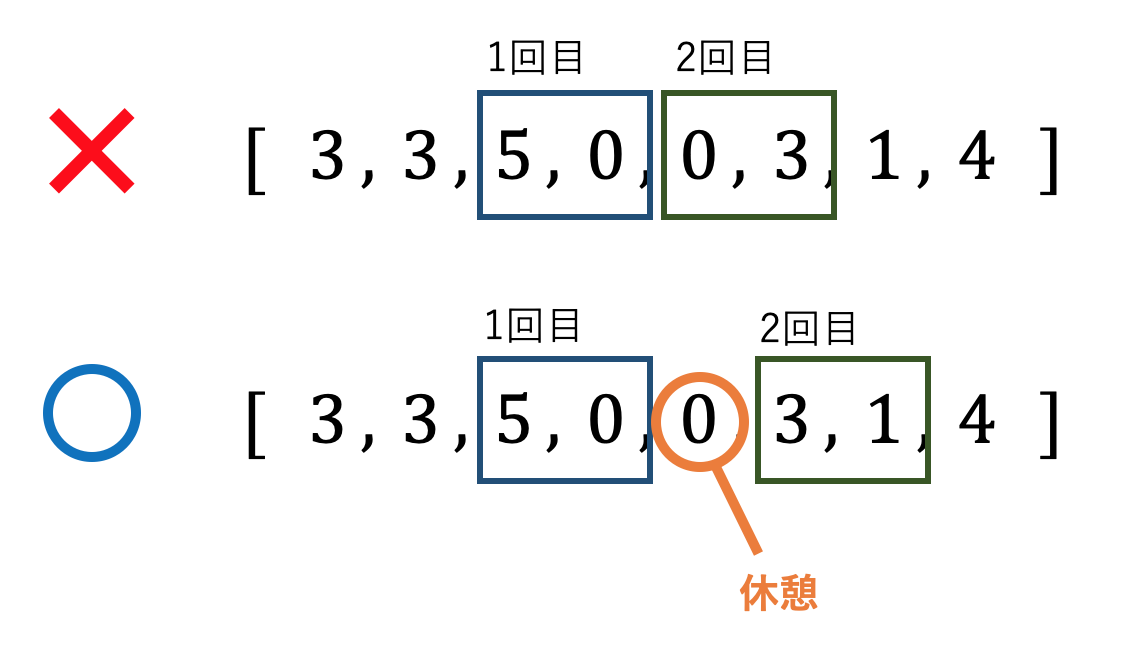
この場合は,Case 3に対して休憩を表す状態$max\_stay$を追加します.そして更新式を以下のようにすれば,休憩を挟んでいる様子を表現できます.
\begin{align}
max\_sell[i+1] &= \max(max\_sell[i], max\_buy[i] + prices[i+1]) \\
max\_buy[i+1] &= \max(max\_buy[i], max\_stay[i] - prices[i+1]) \\
max\_stay[i+1] &= \max(max\_stay[i], max\_sell[i])
\end{align}
max_sell[i+1]は$i$地点までの「買い」の最大利益$max\_buy[i]$に$i+1$地点での「売り」の利益$prices[i+1]$を足したもの,max_buy[i+1]は$i$地点までの休憩を挟んだ後の最大利益$max\_stay[i]$から$i+1$地点での「買い」のコスト$prices[i+1]$を引いたもの,max_stay[i+1]は$i$地点までの「売り」の最大利益$max\_sell[i]$から休憩状態に移行したものです.これをメモリを節約する形で書くと以下のようになります.
def calculate_max_profit(prices: List[int]) -> int:
n = len(prices)
max_stay, max_sell, max_buy = 0, 0, -float("inf")
for i in range(n):
max_stay, max_sell, max_buy = max(max_stay, max_sell), max(max_sell, max_buy + prices[i]), max(max_buy, max_stay - prices[i])
return max(max_stay, max_sell)
まとめ
ここまで網羅的に株価売り買い系問題を見てきましたが,「各座標$i$までの$k$回目の売り買いの最大利益」を表す状態を計算することで多くの問題に対応できることがわかりました.この記事を読んだ方は万が一未来が見通せている状況なら株取引で最大利益をゲットできるようになったはずです.参考にした以下のサイトでコードを実際に動かしてみることができますので,興味を持った方は試してみてください!
参考(LeetCodeより)
Best Time to Buy and Sell Stock
Best Time to Buy and Sell Stock II
Best Time to Buy and Sell Stock III
Best Time to Buy and Sell Stock IV
Best Time to Buy and Sell Stock with Cooldown
Best Time to Buy and Sell Stock with Transaction Fee
(追記)補足:O(n log n)の解法
コメントでさらに最適な方法があることを指摘していただきました.コメント欄に詳細な解説をしていただきましたので詳しくはそちらを参照していただくとして,ここではそれを元にした,Case 4について時間計算量$O(n \log n)$となる実装を載せておきます.
def calculate_max_profit(prices: List[int], k: int) -> int:
prices = [float("inf")] + prices + [float("-inf")] # 両端に無限大の値を挿入
dif_array = [prices[i] - prices[i-1] for i in range(1, len(prices))] # 隣との差を格納した配列
comp_dif = [dif_array[0]] # 圧縮した配列
for i in range(1, len(dif_array)):
if comp_dif[-1]*dif_array[i] < 0:
comp_dif.append(dif_array[i])
else:
comp_dif[-1] += dif_array[i]
max_profit = sum(comp_dif[1::2]) # 何回でも取引可能な場合の最大利益
max_trans = (len(comp_dif)-1)//2 # 最大利益を得る場合の取引回数
if max_trans < k:
return max_profit
value = copy.deepcopy(comp_dif) # 結合後の価値を格納する配列
forwardLength = [1]*len(comp_dif) # 後方に何個分結合されているかを示す配列
backwardLength = [1]*len(comp_dif) # 前方に何個分結合されているかを示す配列
que = [(abs(comp_dif[i]), i, forwardLength[i]) for i in range(len(comp_dif))] # heapを圧縮後配列の各値の絶対値を入れて初期化
heapq.heapify(que)
num = max_trans - k
while que and num: # 多すぎる取引回数の分だけmax_profitから価値を差引いていく
val, i, fi = heapq.heappop(que)
if fi != forwardLength[i]:
continue
start = i - backwardLength[i-1] # 結合する配列の先頭
mid = i + forwardLength[i] # 結合する配列の後半部分の先頭
end = i + forwardLength[i] + forwardLength[i + forwardLength[i]] - 1 # 結合する配列の末尾
forwardLength[start] = backwardLength[end] = end - start + 1
forwardLength[i] = forwardLength[mid] = 0
value[start] = value[start]+value[i]+value[mid]
heapq.heappush(que, (abs(value[start]), start, forwardLength[start]))
max_profit -= val
num -= 1
return max_profit