LRUキャッシュとLFUキャッシュをけっこう丁寧に実装します(Python)

この記事では，検索しても意外と解説が少なかったLRUキャッシュとLFUキャッシュをPythonで丁寧めに実装していきます．特にLFUキャッシュが厄介なのでそちらがメインです．

キャッシュとは

ざっくり言うとキャッシュはよく使うデータを取り出しやすい場所に一時的に保存しておくものです．メモリ上のデータは参照される頻度に差があるので（時間的，空間的局所性など），よく参照されるデータをキャッシュに入れておくことでデータアクセスが高速になります．現代のコンピュータにはまさに必須の構造です．

キャッシュに蓄えられるデータは多くはないため，どのデータを置いておくかというのは重要な問題です．容量いっぱいのキャッシュに新たな要素が入ってきたとき，今保持しているどの要素を捨てるかという選択に関して，最も基本的なものが以下の2つです．

• LRUキャッシュ: Least Recently Used. 直近に参照した時刻が一番古いものを捨てる
• LFUキャッシュ: Least Frequently Used. 過去に参照した回数が一番少ないものを捨てる．複数ある場合は直近に参照した時刻が一番古いものを捨てる

なおここで言う「参照」とは，キャッシュにデータを追加したり，データを見たり，更新したりすること全般だとイメージしてもらえればと思います．これ以降ではこの2つのキャッシュの実装を解説していきます．ただ本記事は「実際にPCで動くキャッシュを作ってみた」という話ではありません．あくまでアルゴリズムの問題として，キャッシュの機能を実現するクラスを書いてみるのが目標です．

ここで扱うキャッシュの定義

ここで扱うキャッシュは，key(int)とvalue(int)のペアを保持するものとします．キャッシュは初期化する際に保持できるデータの個数capacityを指定されます．またキャッシュクラスは以下の関数を持つとします．

• void put(int key, int value): キャッシュに新たなkeyとそれに対応するvalueを追加します．もしキャッシュがいっぱいなら別のデータを放棄する必要があります．
• int get(int key): 入力されたkeyに対応するvalueを返します．もしkeyが存在しなければ-1を返します．

キャッシュ内に存在していないkeyに対してputが行われた場合は新たなkeyが加えられますが，既に存在するkeyに対してputが行われた場合はkeyに対応するvalueが更新されることに注意してください．一方getはkeyに対応するvalueを参照するだけで，要素の追加や削除は行いません．まとめると，以下のクラスの各関数を記述する問題になります．

class Cache:
    def __init__(self, capacity: int):
        ...

    def put(self, key: int, value: int): -> int:
        ...
  
    def get(self, key: int): -> int:
        ...

LRUキャッシュの実装

はじめに述べたように，LRUキャッシュは，新しいデータが入ってきた場合に，直近に参照した時刻が一番古いデータを捨てるようなものです．ポイントとなる操作をまとめると

• PUT
  • 新たな(key, value)ペアを追加する操作
  • keyに対するvalueを更新する操作
  • 参照された時刻が最も古い(key,value)ペアを削除する操作
• GET
  • keyに対応するvalueを探す操作
• 両方
  • keyが参照された時刻（順番）を記録，更新する操作

で，これをキャッシュサイズに関わらず全て$O(1)$の時間計算量で行うことが目標です．本記事では一般的な実装と，pythonのOrderedDictを使った実装を説明します．

方法1: Linked List + Dict

もっとも単純な方法は，例えば辞書$dict$などを用意しておき，そこにkey，value，参照時刻を記録しておくことです．この場合，$get$関数や要素の追加は$O(1)$で行えますが，古い要素を削除したいときに全要素の参照時刻を確認する必要があり，$O(n)$ ($n$はキャッシュのcapacity)の時間がかかってしまいます．非常に簡易的に書くと以下のような感じです．

class LRUCache:
  def __init__(self, capacity: int):
    self.d = dict()
    self.capacity = capacity

  def put(self, key: int, value: int): -> int:
    self.d[key] = [value, time.time()]  # (value, 参照時刻)を追加
    if len(self.d) > self.capacity:  # 容量オーバーした場合
        k, v = min(d.items(), key=lambda x: x[1][1])  # 参照時刻が一番小さい（古い）ものを取り出す，　O(n)かかる
        del self.d[k]
  
  def get(self, key: int): -> int:
    self.d[key][1] = time.time()  # 参照時刻を更新
    return self.d[key][0]  # valueを返す

時刻を記録する代わりに，連結リスト(Linked List)を使う方法はどうでしょうか？連結リストとは，各データが次の要素へのポインターを持ち，列になったようなデータ構造です．データの追加や削除を$O(1)$で行うことができます．

これを時間順に結合していけば，時刻を記録しなくても最後にある要素が最も古いデータを表すことになり，削除すべきデータを$O(1)$で探索できます．しかし連結リストは特定のkeyに対応するvalueを検索するのに，先頭から連結リストを探索しなければならず，今度は$get$関数に最大$O(n)$の時間がかかってしまいます．

どうしたらいいのでしょう？両者に長所と短所があるのなら，両方使ってみてはどうでしょうか？

以下のように役割を分担します．

• 連結リスト: keyとvalueを格納したノードを参照時刻が新しい順に並べる
• 辞書: keyとそれに対応するノードを保持する

これにより，

• get: まず辞書を見てkeyに対応する連結リストのノードを調べ，そこに書かれたvalueを返す．その後そのノードを連結リストの先頭に移動する

- **put**: まず辞書を見てkeyが存在するかを調べる． - 存在していれば対応するノードのvalueを上書きし，連結リストの先頭に持ってくる． - 存在していなければ新たにノードを作成し連結リストの先頭におく．その際もしノードの個数がキャッシュの容量を超えてしまったら，連結リストの最後のノードと，それに対応する辞書の要素を削除する．

ややこしいので実装を見てもらったほうが早いかもしれません．まず連結リストのノードを定義します．

class ListNode:
    def __init__(self, key, value):
      self.key = key
      self.value = value
      self.prev = None
      self.next = None

$prev$，$next$はそれぞれ自分の前と後にあるノードを指すポインターです．さらに，わかりやすいように連結リストのクラスを作ります．

class DoubleLinkedList:
    def __init__(self):
        self.head = ListNode(0, 0)  # ダミーの先頭ノード
        self.tail = ListNode(0, 0)  # ダミーの末尾ノード
        self.head.next = self.tail
        self.tail.prev = self.head
        
    def add_node(self, node: ListNode) -> None:  # 先頭ノードの直後にノードを挿入
        node.prev = self.head
        node.next = self.head.next
        self.head.next = node
        node.next.prev = node
            
    def remove_node(self, node: ListNode) -> None:  # ノードを削除
        node.prev.next = node.next
        node.next.prev = node.prev
    
    def move_to_head(self, node: ListNode) -> None:  # ノードを先頭に移動．つまりノードを削除し先頭に追加
        self.remove_node(node)
        self.add_node(node)

自分の前後のノードのポインターを持っているためDonbleLinkedListとしています．ここで連結リスト作成のテクニックとして，初期化の際に先頭と末尾のダミーノード$head, teil$を作成しています．これによって様々な操作を行う際に参照エラーが起きてしまうのを防いでいます．$add\_node()$関数は先頭ノードの直後にノードを移動する関数，$romove\_node()$関数はノードを削除する関数，$move\_to\_head()$関数は両方をまとめてやってくれる関数（既にあるノードを先頭に移動してくれる関数）です．

これを使ってメインクラスを実装します．

class LRUCache:
    def __init__(self, capacity: int):
        self.capacity = capacity
        self.key_to_node = dict()
        self.linked_list = DoubleLinkedList()

    def get(self, key: int) -> int:
        if key not in self.key_to_node:  # keyがない場合
            return -1
        else:  # keyがある場合
            self.linked_list.move_to_head(self.key_to_node[key])  # 先頭に移動
            return self.key_to_node[key].value
            
    def put(self, key: int, value: int) -> None:
        if key in self.key_to_node:  # keyがある場合，valueを更新
            self.key_to_node[key].value = value
            self.linked_list.move_to_head(self.key_to_node[key])
        else:  # keyがない場合，新たに作って追加
            new_node = ListNode(key, value)
            self.key_to_node[key] = new_node
            self.linked_list.add_node(new_node)
            
            if len(self.key_to_node) > self.capacity:  # 容量を超えてしまった場合
                del self.key_to_node[self.linked_list.tail.prev.key]  # 辞書の削除
                self.linked_list.remove_node(self.linked_list.tail.prev)  # 連結リストの削除

init

初期化部分では，最大容量の$self.capacity$，keyから対応するノードへの辞書である$self.key\_to\_node$，連結リスト$self.linked\_list$を定義します．

get

$get$関数は，keyがなければ-1，あれば対応するvalueを返します．さらに，参照されたノードを連結リストの先頭に移動します．$self.key\_to\_node[key]$はノードを表していることに注意してください．

put

$put$関数はまずkeyが既に存在するかどうかで場合分けします．存在すれば，valueを更新してノードを先頭に移動します．存在しなければ新たにノードを作って連結リストの先頭に追加します．その際に$capacity$を超えてしまった場合は，辞書と連結リストから最も古い要素を削除しています．

様々な構造が出てきてややこしいですが，何をやっているかを理解すれば，各操作を$O(1)$で行うためにこの構造が効果的だとわかっていただけると思います．

方法2: OrderedDict

方法1がベーシックなやり方ですが，pythonでは同じ仕組みを実現する裏技的な方法があります．それはcollections.OrderedDictを使うことです．通常のPythonのDictは単に(key,value)ペアを記録するだけですが，OrderedDictはkeyを参照した順序を記憶しているという特徴があります．また，$popitem()$関数によって最初または最後に参照した要素を取り出すことができます．解法1では順序を記憶するために連結リストを導入しましたが，辞書が順序を覚えておいてくれるならもう連結リストは必要ありません．以下のように簡潔に実装できます．

class LRUCache:
    def __init__(self, capacity: int):
        self.d = collections.OrderedDict()
        self.capacity = capacity

    def get(self, key: int) -> int:
        if key not in self.d:
            return -1
        
        value = self.d.pop(key)  # keyを一度削除
        self.d[key] = value  # keyを改めて追加
        return value

    def put(self, key: int, value: int) -> None:
        if key in self.d:
            self.d.pop(key)
        self.d[key] = value
        if len(self.d) > self.capacity:
            self.d.popitem(last=False)  # 最も古い要素を削除

ここでは，要素を先頭に移動させる際に，一度$pop(key)$で要素を削除し，再度追加することで参照時刻を最新にしています．ちなみに，$popitem(last=True)$とすると最も新しい要素を削除することもできます．

LFUキャッシュの実装

さて，LRUキャッシュの実装を見てきましたが，まあここまではよくある話です．これ以降はメインテーマのLFUキャッシュを実装していきます．，こちらでも$put$と$get$操作を$O(1)$で行うのが目標です．改めて整理しておきますが，LFUキャッシュのルールは

• 既にある要素のうち参照回数が最も少ないものを削除する
• 参照回数が少ない要素が複数あれば，最後に参照した時刻が最も古いものを削除する

です．つまり参照回数と参照時刻を両方保持しておく必要があります．回数だけ気にしておけばいいなら参照回数とkeyのペアを辞書か何かで保持しておけばなんとかなりそうな気もしますが，参照時刻も考えるとそう簡単にはいかなくなります．

ここでは，参照回数ごとに連結リストを保持することを考えます．全体の構造は下の図のようになります．要素を削除する際にはまず一番少ない参照回数の連結リストにアクセスし，そのリストの最後尾のノードを削除すれば$O(1)$で行うことができます．

しかし，ノードが参照されるとその度に参照回数が増えるので，別の連結リストに移動させる必要が出てきます．さらに現時点の最小回数が何回なのか正しく保持しておかないと即座に最小の連結リストにアクセスできません．このような複雑な構造をどう実現するのか，実際に実装を見ていきます．まずは連結リストのノードです．

class ListNode:
    def __init__(self, key, val):
        self.key = key
        self.val = val
        self.freq = 1  # 参照，更新された頻度
        self.prev = None
        self.next = None

LRUキャッシュの場合とほとんど変わりませんが，参照回数を中に保持しておくことにします．次に連結リストのクラスです．

class DoubleLinkedList:
    def __init__(self):
        self.head = ListNode(0, 0)
        self.tail = ListNode(0, 0)
        self.head.next = self.tail
        self.tail.prev = self.head
        self.length = 0
        
    def __len__(self):
        return self.length
        
    def add_node(self, node):
        node.prev = self.head
        node.next = self.head.next
        self.head.next = node
        node.next.prev = node
        self.length += 1
        
    def remove_node(self, node):
        node.prev.next = node.next
        node.next.prev = node.prev
        self.length -= 1

これも，リストの長さを記録する$self.length$が増えた以外はLRUキャッシュの場合とほぼ同じです．これを使ってメインクラスを実装します．

class LFUCache:
    def __init__(self, capacity: int):
        self.key_to_node = dict()  # keyからノードへの辞書
        self.list_map = collections.defaultdict(DoubleLinkedList)  # 参照回数ごとの連結リスト
        self.capacity = capacity
        self.total_size = 0  # キャッシュ内の全てのデータ数
        self.min_freq = 0  # 最小参照回数

    def get(self, key: int) -> int:
        if key not in self.key_to_node:
            return -1
        
        node = self.key_to_node[key]
        self.update(node)        
        return node.val

    def put(self, key: int, value: int) -> None:
        if key in self.key_to_node:  # keyが既に存在している場合
            node = self.key_to_node[key]
            node.val = value
            self.update(node)
        else:  # keyが存在していない場合
            if self.total_size == self.capacity:  # capacityを超えたらノードを一つ削除
                last_node = self.list_map[self.min_freq].tail.prev  # 削除するノードを取り出す
                self.list_map[self.min_freq].remove_node(last_node)
                del self.key_to_node[last_node.key]
                self.total_size -= 1
                
            node = ListNode(key, value)  # 新たなキーに対応するノードを作成する
            self.key_to_node[key] = node  # 辞書に追加
            self.list_map[1].add_node(node)  # 参照回数1の連結リストに追加
            self.min_freq = 1  # 最小参照回数は1
            self.total_size += 1
            
    def update(self, node):  # 参照，更新されたノードを移動する
        current_freq = node.freq
        self.list_map[current_freq].remove_node(node)
        node.freq = current_freq+1
        self.list_map[current_freq+1].add_node(node)
        if current_freq == self.min_freq and len(self.list_map[current_freq]) == 0:  # 最小参照回数を更新する場合
            self.min_freq = current_freq+1

init

まず初期化部分ですが，keyと対応するノードを示す$self.key\_to\_node$はLRUキャッシュと同じです．しかし，連結リストはLRUキャッシュでは単一のものだったのに対し，ここでは$self.list\_map$として，各回数に対応する連結リストがそれぞれ入っているような構造になっています．$self.total\_size$はキャッシュ内のデータ数，$self.min\_freq$は現在キャッシュの中にあるデータのうち最小の参照回数を保持する変数です．

update

次に，新たに出現した$update()$関数について説明します．これは参照されたノードを移動する関数です．あるノードが参照された場合，そのノードは参照回数が増えるため，回数の一つ多い連結リストに移動しなくてはなりません．よって

• 今いる連結リストからノードを削除する．
• ノードの参照回数を+1する
• 一つ参照回数の多い連結リストの先頭へ移動する

という操作を行います．

さらに，もしノードを削除したことでもといたノードが長さ0になった場合は注意が必要です．もしその参照回数が最小だった場合，もうそこにノードはないので$self.min\_freq$を更新しなければなりません．幸い，$self.min\_freq+1$に移動後のノードがあることは明らかなので，$self.min\_freq$に+1すれば大丈夫です．

get

updateを定義してしまえばget関数は簡単です．もしkeyが存在しなければ-1を返し，keyが存在すればvalueを返します．その際にupdate関数を実行しておけば十分です．

put

一方put関数はより複雑です．まず，keyが存在している場合は，valueの値を更新するだけなのでほとんどgetと変わりません．

問題はkeyが存在しないときです．新たなkeyを追加したいのですが，まず容量がいっぱいでないか確認しなければなりません．もしいっぱいなら要素を一つ削除します．削除対象の要素は参照回数が最も少ない連結リストの最後の要素です．手順は次のようになります．

• $self.min\_freq$の値から最小の連結リストにアクセスする．
• 最小の連結リストの最後のノードにアクセスする．
• そのkeyをもとに$self.key\_to\_node$から要素を削除する
• 連結リストのノードも削除する
• $self.total\_size$を-1する

ただ，一つ問題があります．もし削除後の連結リストが空になってしまった場合，$self.min\\_freq$はどのように更新すればいいのでしょうか？今回は$get$関数のように+1すればいいとは限りません．

しかしこの心配は杞憂に終わります．なぜなら直後に新しいノードを追加するからです．新たに追加されたノードは常に参照回数が1なので，問題なく$self.min\_freq = 1$と更新できるわけです．追加の手順は以下のようになります．

• 入力されたkey, valueをもとに新しいノードを作成する
• $self.key\_to\_node$にkeyとノードのペアを追加する
• ノードを$self.list\_map$の回数1の部分に追加する
• $self.min\_freq = 1$とする
• $self.total\_size$を+1する

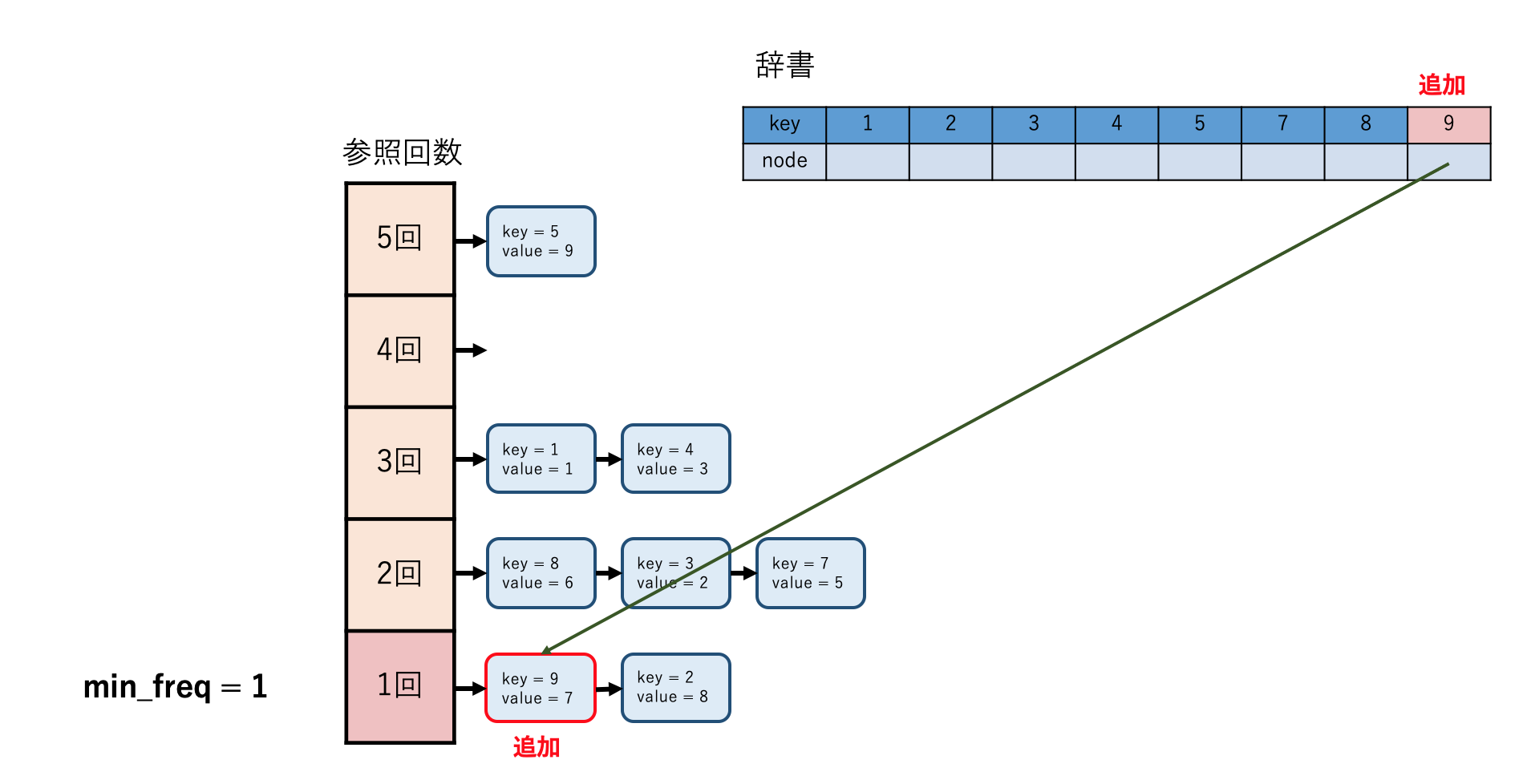
このように，データ構造とそれに対する操作によく注意して構築することで，全ての操作を無事$O(1)$で行うことができました．

まとめ

LRUキャッシュとLFUキャッシュについて実装の紹介をしてきました．初見だと非常に複雑に思えるかもしれませんが，コンピュータにおいてはとても重要かつ基本的な構造ですのでぜひ理解していただければと思います．

参考
LRU-cache
LFU-cache