突然ですが,この山って一体どれくらい水が溜まると思いますか?

上から雨が降ったらたぶんこんな感じで池ができるはずです.

この山を,縦横1マスを1とする座標系に置いた場合,溜まる水の量を数えてみると6になります.このもし山が巨大になったら,水の量はどうやって求めればいいのでしょうか?
さらに,こんな感じで立体的にした山はどうでしょうか?溜まる水の量,気になってきませんか?
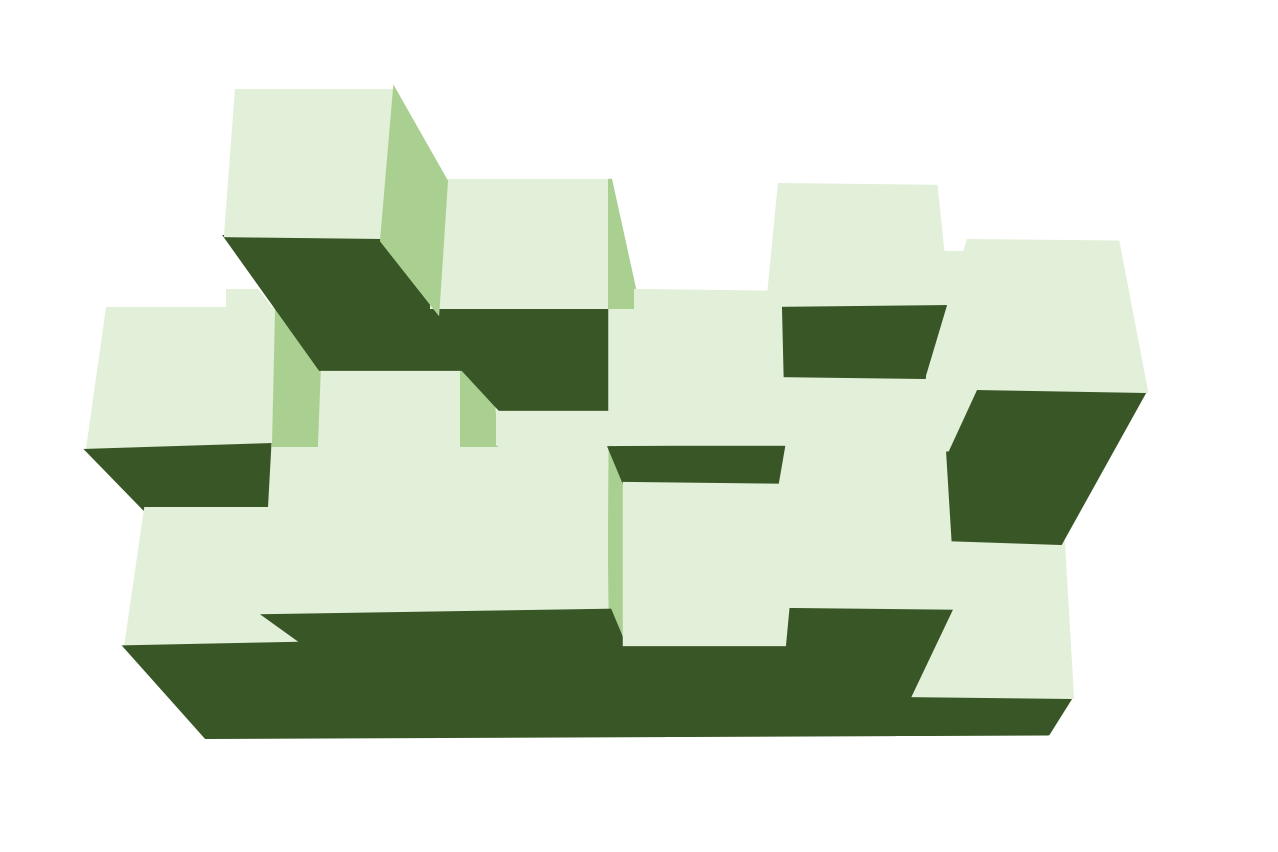
皆さんがどの程度共感してくださるかはさておき,実はこの問題はコーディング面接の教科書にも載っているような有名な問題です.その解法が面白かったので紹介していきたいと思います.
2次元の山
まず山が方向と高さを持つ2次元の場合を考えます.
山の高さを配列で表現すると,この問題は,各地点の高さを表現する配列 $height = [0,1,0,2,1,0,1,3,2,1,2,1]$ を入力とし,溜まる水の量を返す関数を設計する問題と捉えることができます.
def trap_water(height: List[int]) -> int:
...
return capacity
解法1
この問題を初めて見た場合,どうやって水の量を計算するのか思いつくのは簡単ではないと思います.しかし,各$x$座標において溜まる水の量を考えるとあることに気付きます.ある地点の両側を見て,両側に現在地より高い地点があった場合,それらのうち低い方の高さまで水がたまるのです.例えば初めの図で $x = 4$ の地点を見てみると,右側では $x = 2$ が高さ2で最高,左側では $x = 6$ が高さ3で最高です.$x = 4$ は高さ0なので,水は $2 - 0 = 2$ 溜まるとわかるのです.
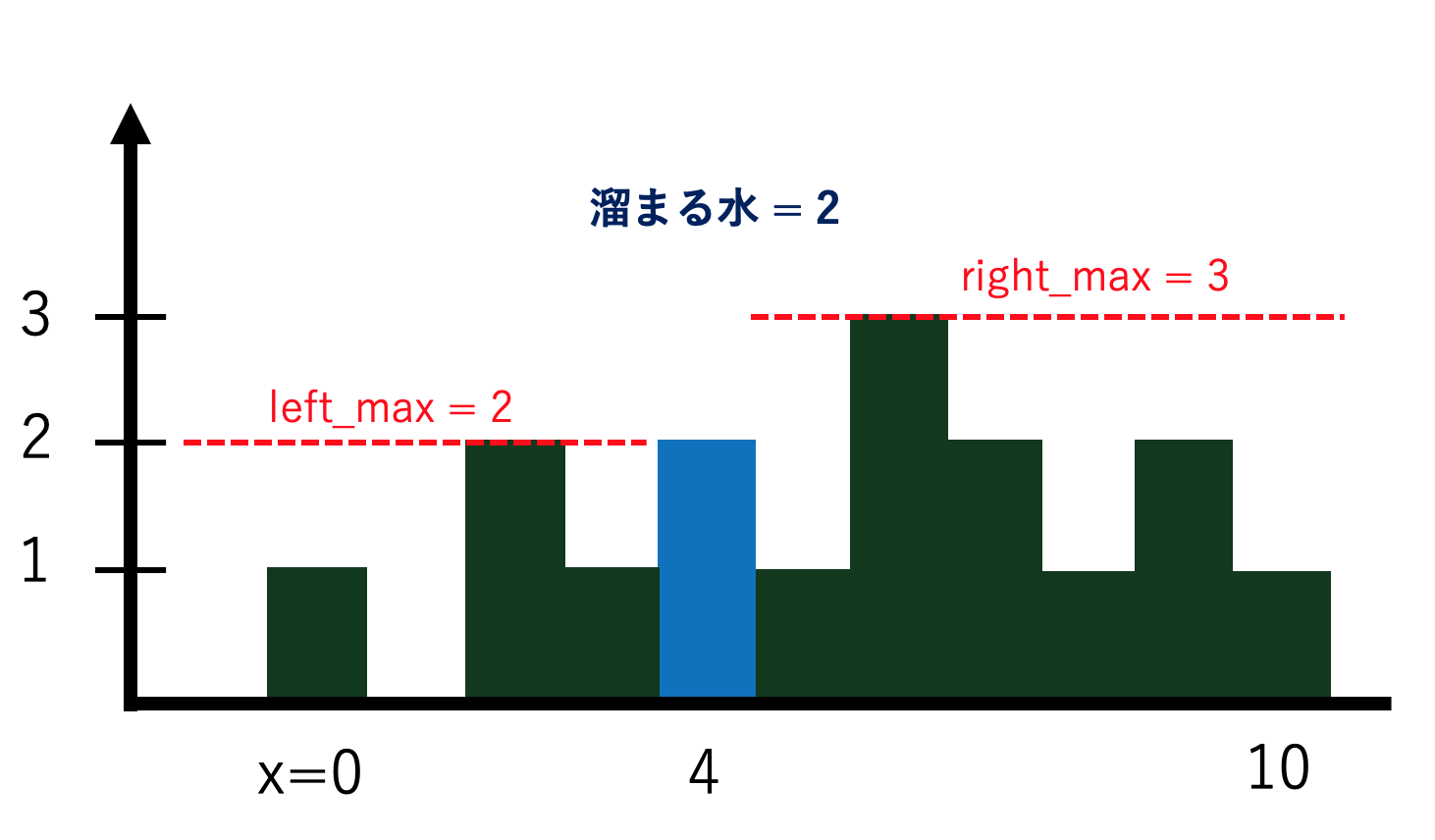
より一般化すると,$x = i$ 地点で溜まる水は以下のように書けます.
water[i] = \max(0, \min(\max(height[:i]),\max(height[i+1:])) - height[i]))
これをコードに落とし込むと以下のようになります.
def trap_water(height: List[int]) -> int:
if not height:
return 0
n = len(height)
capacity = 0
for i in range(n):
left_max = max(height[:i]) if i > 0 else 0
right_max = max(height[i+1:]) if i < n-1 else 0
capacity += max(0, min(left_max, right_max) - height[i])
return capacity
これは,各x座標について右側,左側を計算するので,時間計算量は$O(n^2)$となります.一方空間計算量は$O(1)$で済みます.
解法2
基本的に$O(n^2)$の解法はもっと速くしたいなという欲が湧きます.解法1では各$x$座標について両側の最高地点を計算していましたが,$x=i$での計算と,$x=i+1$での計算はほとんど一緒のことをしています.具体的には,$x=i$から左側の最高地点は,$x=i-1$から左側の最高地点と$x=i$の高さを比べて高い方です.これを毎回最初から計算するのは無駄ですので,値を保存しておけば良いという発想になります.
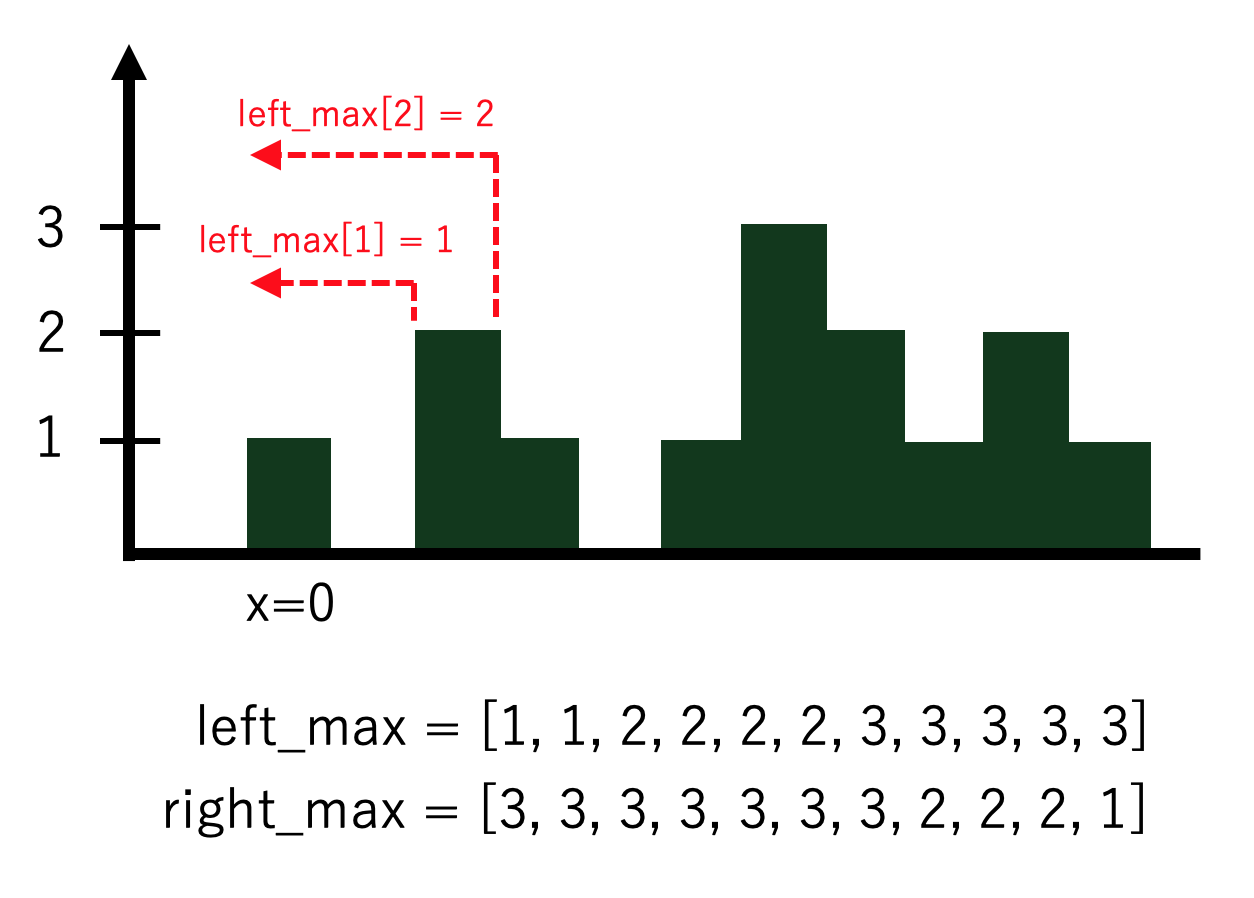
まず,$x=i$地点から左側の最高地点を保存する配列$left\_max$を作ります.$left\_max[i]$は$x = 1,...,i$それぞれに対する値を保存います.$left\_max$には以下のような関係が成り立ちます.
left\_max[i] = max(left\_max[i-1], height[i])
同じように,$x=i$地点から右側の最高地点を保存する配列$right\_max$は以下の関係が成り立ちます.
right\_max[i] = max(right\_max[i+1], height[i])
これを先に作っておけば,$x=i$で溜まる水の量は解法1と同じように,
water[i] = \max(0, \min(left\_max[i-1],right\_max[i+1]) - height[i]))
と書けます.これのコードは以下のようになります.
def trap_water(height: List[int]) -> int:
if not height:
return 0
n = len(height)
capacity = 0
left_max, right_max = [0]*n, [0]*n
left_max[0], right_max[-1] = height[0], height[-1]
for i in range(1,n):
left_max[i] = max(left_max[i-1], height[i])
for i in reversed(range(n-1)):
right_max[i] = max(right_max[i+1], height[i])
for i in range(1,n-1):
capacity += max(0, min(left_max[i-1], right_max[i+1]) - height[i])
return capacity
この場合,配列を順に見る操作を3回行うだけなので時間計算量は$O(n)$になります.空間計算量は,$left\_max$,$right\_max$を保持している分$O(n)$になります.
なお,$right\_max$の計算と$water$の計算を同時に行うことで,オーダーは変わりませんが時間計算量と空間計算量を1回分減らすことができます.
def trap_water(height: List[int]) -> int:
if not height:
return 0
n = len(height)
capacity = 0
left_max = [0]*n
left_max[0] = height[0]
for i in range(1,n):
left_max[i] = max(left_max[i-1], height[i])
right_max = height[-1]
for i in reversed(range(1,n-1)):
capacity += max(0, min(left_max[i-1], right_max) - height[i])
right_max = max(right_max, height[i])
return capacity
解法3
時間計算量と空間計算量が$O(n)$になれば大抵の人は満足します.しかし実はこの手法はさらに改善することができます.
解法1と2では$x=i$地点の両側の高さから溜まる水の量が決まることがわかりましたが,もっと言えば両側のうち低い方の高さで溜まる水の量が決まります.そこで,両側から同時に高さを数えていき,それを発見しようというのがこの手法です.
山の両側にポインターをおきます.つまり$x=0$に$pl$,$x=n-1$に$pr$というポインターをおきます.そして手順に従い,$pl$を右方向に,$pr$を左方向に動かしていきます.さらに,これまで見た最高地点として$max\_height$という値を記録しておきます.これは初めは0に初期化しておきます.
問題はどのようにポインターを動かすかなのですが,まず$height[pl]$と$height[pr]$,つまりポインタ地点での高さを比べます.そして,小さかった方に対して以下の2つの操作を行います.
- $max\_height$とポインター地点の$height[p]$を比べる
- $max\_height$の方が大きければ,p地点に溜まる水の量は$max\_height - height[p]$となる
- $height[p]$の方が大きければ水は溜まらない.$max\_height$を$height[p]$に更新する.
- ポインターを一つ先へ進める.
なお$pl$と$pr$をまとめて$p$と書きました.これを,$pl$ < $pr$である限り続けます.
さて,これは一体何をしているのでしょうか?手順にそって実際に動かしてみるとわかるのですが,$x <= pl$と$pr <= x$,つまり2つのポインターから外側の最高地点は$max\_height$よりも高く,かつどちらか一方はちょうど$max\_height$と同じになることがわかります.例えばポインター$pl$を動かすことになった場合,
- もし$height[pl] >= max\_height$なら水は溜まらない
- $height[pl] < max\_height$なら, $x < pl$の領域にはちょうど高さ$max\_height$の地点があり,$pr <= x$の領域には高さ$max\_height$以上の地点がある
が成り立っているのです.ということは必然的に,溜まる水の量は$max(max\_height - height[p], 0)$となります.
9ステップ目まで順に動かすと以下の図のようになります.なんとなくイメージが掴めるでしょうか...?なお.$height[pl] = height[pr]$の時は$pr$を移動させていますがどちらでも構いません.最終的には全体で最も高い地点に$pl$と$pr$が集合します.

また,コードは以下のようになります.
def trap_water(height: List[int]) -> int:
if not height:
return 0
left, right = 0, len(height)-1
max_val = capacity = 0
while left < right:
if height[left] <= height[right]:
cur_val = height[left]
left += 1
else:
cur_val = height[right]
right -= 1
capacity += max(0, max_val - cur_val)
max_val = max(max_val, cur_val)
return capacity
この場合,時間計算量は$O(n)$のままですが,最高地点を保持する必要がなくなったので空間計算量は$O(1)$にすることができました.
3次元の山
次は山が3次元の場合について考えていきます.3次元の山というのはこんな感じのやつです(手書きなのでガタガタで恐縮ですが).
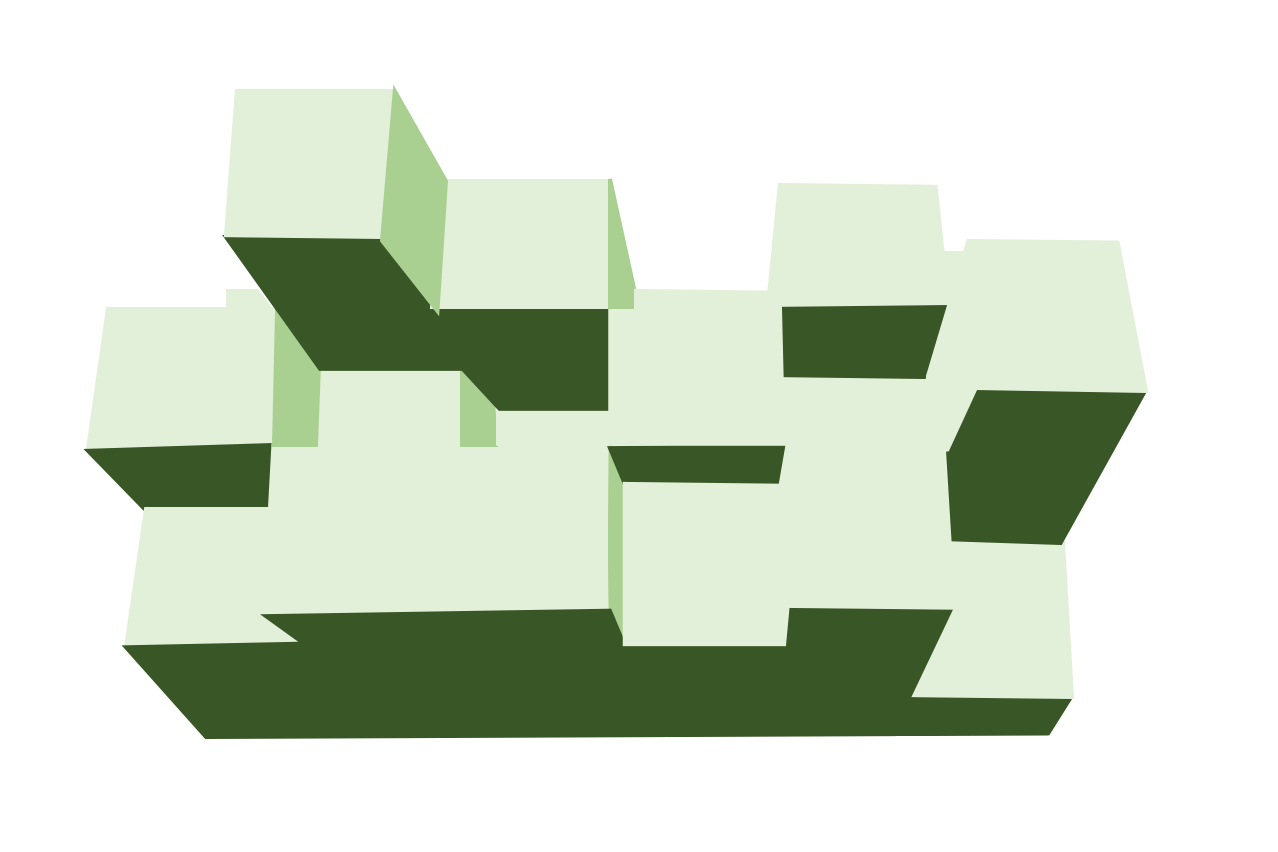
この場合,入力が以下のような配列になります.
\begin{align}
height = [&[1,4,3,1,3,2],\\
&[3,2,1,3,2,4],\\
&[2,3,3,2,3,1]]
\end{align}
少し考えてみるとこれが2次元の山に比べてかなり複雑になったのがわかると思います.2次元の時は両側の高さを考えればよかったものが,色んな方向の水の流れを考えなくてはいけません.大きな山だと人が考えても間違えてしまいそうです.
解法
この問題は,2次元の場合の解法3を応用して解くことができます.解法3において,2次元の場合は両端に2つのポインターを用意し,小さい方を内側に移動させましたが,これは
- 一番外側にある位置にポインターを置いてスタートする
- 最も小さいポインターを選んでその位置に対して水量の計算などの操作を行う
- その位置から移動できる場所へポインターを移動する
という操作をしていると言い換えることもできます.これに従って3次元の操作へと拡張します.つまり,
1.始め平面の外周全てにポインターを置く
2.それらの中から高さが一番低い点を選ぶ
3.その地点の水の高さを求める
4.$max\_height$を更新する
5.その位置から到達可能でまだポインターを置いていない位置にポインターを置く
6.ポインターがなくなるまで2から5を繰り返す
とするのです.この操作を繰り返すと下のようになります.
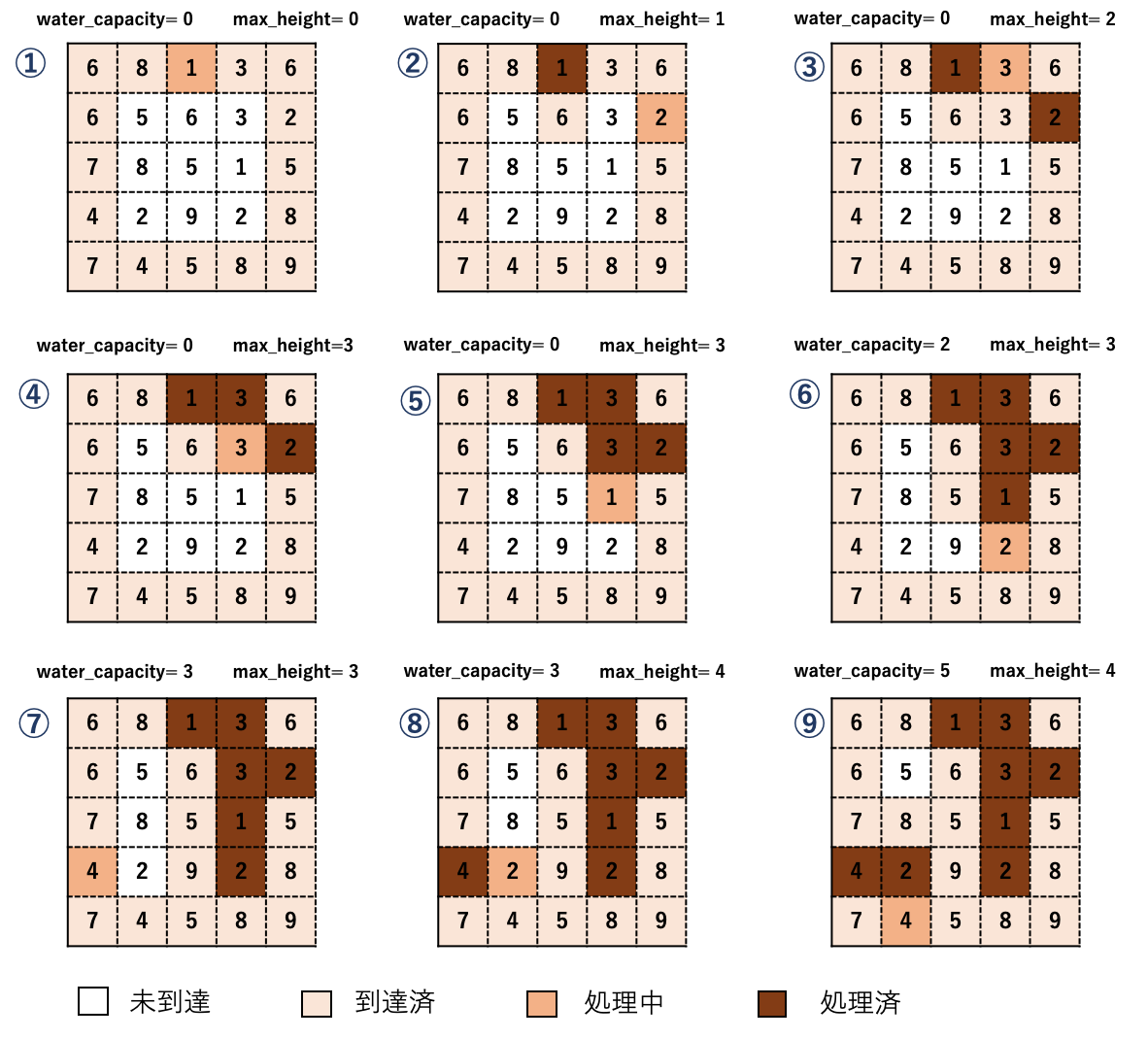
これを見ればわかるように,平面上には常に「到達済」ブロックによる外周の輪っかができており,それらは$max\_height$以上の壁となってます.よって$\max(max\_height-height[p], 0)$で水の高さが求まるのです.
さて,これを実現するコードですが,ポインターが置かれた座標の集合に対して,集合の最小値を取り出す操作と集合に要素を追加,削除する操作があるので,ヒープ(優先度付きキュー)が最適です.ヒープは要素の追加と削除が$O(\log n)$で,最小値の検索が$O(1)$で行えます.
def trap_water_3d(self, height: List[List[int]]) -> int:
if not heightMap or not heightMap[0]:
return 0
h, w = len(heightMap), len(heightMap[0])
if h <=2 or w<=2:
return 0
visited = [[False]*w for _ in range(h)]
que = []
for i in range(h):
que.append((heightMap[i][0], i, 0))
que.append((heightMap[i][w-1], i, w-1))
visited[i][0] = visited[i][w-1] = True
for j in range(w):
que.append((heightMap[0][j], 0, j))
que.append((heightMap[h-1][j], h-1, j))
visited[0][j] = visited[h-1][j] = True
heapq.heapify(que)
max_val = capacity = 0
while que:
val, r, c = heapq.heappop(que)
capacity += max(0, max_val - val)
max_val = max(max_val, val)
for dr, dc in [(1,0), (-1,0), (0,1), (0,-1)]:
if 0<=r+dr<h and 0<=c+dc<w and not visited[r+dr][c+dc]:
visited[r+dr][c+dc] = True
heapq.heappush(que, (heightMap[r+dr][c+dc], r+dr, c+dc))
return capacity
ここではまず外周の座標とその高さを$que$に入れます.$visited$は既に訪れた座標を意味します.$que$から最小の要素を取り出し,その地点の水量を$capacity$に加算するとともに,最高地点の高さ$max\_val$を更新します.そして,現在の座標から隣接する4地点のうち,まだ訪れていない地点を$que$に入れます.これを$que$が空になるまで続けることで全てのマスを走査できます.時間計算量ですが,マス目の数を$n$とすると,各地点に対して$que$への追加と取り出しが高々1回ずつ行われるため,$O(n \log n)$となります.また空間計算量は座標を保存する$que$の容量で$O(n)$となります.
さらに,この考え方を応用すればさらに高次元の山に溜まる水の量を求めることもできるはずです.各地点の高さが入れられたn次元行列に対して,外周をスタート地点としヒープを使って走査していけばいいのです.この記事を読んだ方は,もう既に4次元の山に溜まる水を求められるようになっているはずです.
まとめ
ここまで山に溜まる水の量を計算してきました.この知識で,皆さんもぜひお近くの山にたまっている水の量を求めてみてください(?)
参考(LeetCodeより)
Trapping Rain Water
Trapping Rain Water II
