量子アニーリングの説明でよく見かけるポテンシャル図についてコメント

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

概要

量子アニーリングをする際のスピン配位の状態空間がどのような多様体になっているか確認します。

参考

下記サイトを参考にしました。

• 物理のいらない量子アニーリング入門

手順

量子力学の状態空間

量子アニーリングの大域解の探索における説明でしばしば次のような図を見ます。

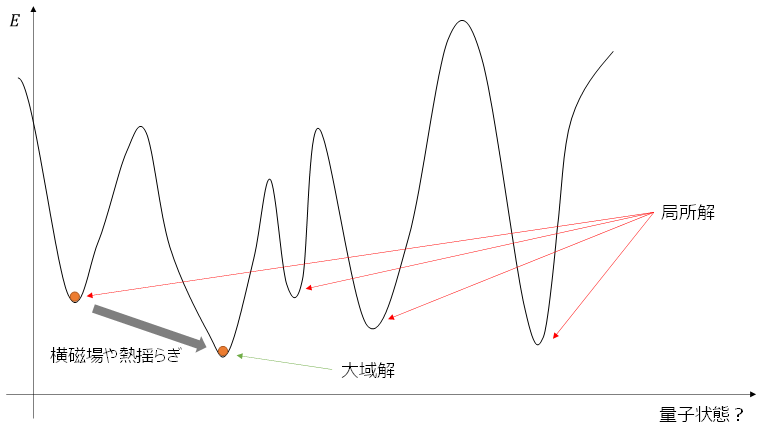
図は量子アニーリングのそれぞれのスピン配位でのエネルギーを表しています。これを古典計算機で実現する場合を考えます。谷に落ち込んだ状態はエネルギーが低くなっているので、山を越えることができません。山を越えるためには外からエネルギーをもらう必要があるからです。量子モンテカルロ法では横磁場によって山を確率的に越えることができます。シミュレーテッドアニーリングでは熱浴からもらうランダムな熱エネルギーによって確率的に山を飛び越えることができます。

ところで、横軸の量子状態の厳密な意味はなんでしょうか。以降は量子コンピュータを考え、量子状態について考えてみましょう。
量子状態は複素係数で表すことができます。まず1粒子状態で考えてみましょう。1粒子状態のスピンは二つの複素数で表現できました。

\ket{\sigma} = \alpha\ket{1} + \beta\ket{-1}.

では量子状態は複素2次元空間なのでしょうか。実は違います。量子力学の状態空間は、

1. 規格化されていること
2. 全体の位相は同一視すること

が必要になります。したがって全体の位相の同一視を$\sim_2$と書くことにすると、2.を満たす空間は$X = \mathbb C^2/\sim$と書けます。$X$は実3次元空間で、$X$から原点を除いた空間に次の同値関係を入れます。

(x_1,x_2,x_3)\sim_1 (rx_1,rx_2,rx_3) , \ r\in \mathbb R_+.

これによって規格化1.が満たされます。この条件によって規格化が満たされ、$Y = (X- \{ 0 \})/\sim_1$が状態空間となります（1.の条件は正確には同値ではなく、半径1を要求します）。これによって状態空間は$Y = S^2$になります。

もう少し具体的な計算で見てみます。まず、状態の全体の位相は無視できるので$\alpha$を実数にすることができます。$\alpha = ae^{i\theta}$とかけば次のように書けます。

\ket{\sigma} = a\ket{1} + \beta\ket{-1}.

さらに$\beta = b + ic$と書けば規格化条件は次のように書けます。

a^2 + b^2 + c^2 = 1.

これは$S^2$を表しています。

2粒子状態の場合はどうでしょうか。2粒子状態のスピンは四つの複素数で表現できました。

\ket{\sigma} =c_1\ket{1}\ket{1} + c_2\ket{1}\ket{-1}+c_3\ket{-1}\ket{1}+c_4\ket{-1}\ket{-1}.

1粒子状態と同様にして$c_1 = ce^{i\theta}$と書けば全体の位相を無視して次のように書けます。

\ket{\sigma} =c\ket{1}\ket{1} + c_2\ket{1}\ket{-1}+c_3\ket{-1}\ket{1}+c_4\ket{-1}\ket{-1}.

規格化条件は$c_i = a_i + b_i$とかけば規格化条件は次のようになります。

c^2 + \sum_{i=2}^4(a_i^2 + b_i^2)=1.

よって状態空間は$S^6$となります。

同様にして$N$粒子状態のときは状態空間は$S^{2(2^N-1)}$となります。したがって図の横軸は$S^{2(2^N-1)}$の座標となるわけです。

観測可能な状態

これで状態空間のトポロジーは明らかになったわけですが、もう少し考えてみましょう。状態空間は$S^{2(2^N-1)}$の座標点で表されますが、これは量子状態、すなわち重ね合わせ状態も含んでいます。しかし、量子コンピュータの最後の計算で観測を行いますので、実現できるのは各係数が1のときのみです。例えば2粒子状態で観測できる状態は$c_1 = 1$または$c_2 = 1$または$c_3 = 1$または$c_4 = 1$の状態のみです。したがって$S^6$上の離散的な4点のみです。$N$粒子の時は$S^{2(2^N-1)}$上の$2^N$点のみが実現されます。重ね合わせまで含めた大域解と、観測で実現できる最低エネルギー解は異なる場合があります。

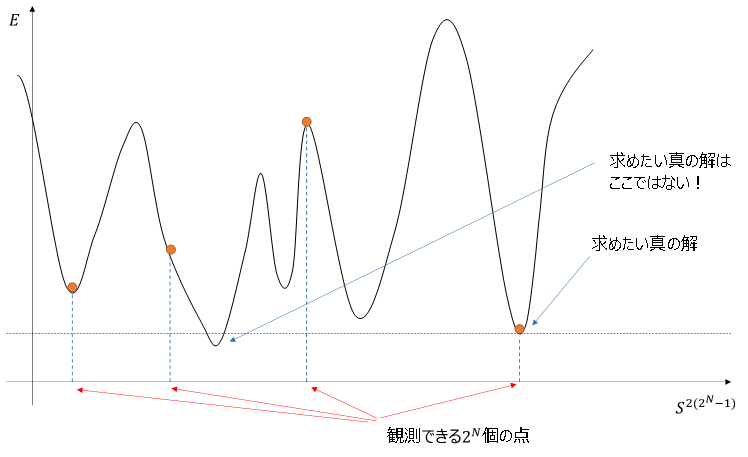
したがって古典計算機の場合の厳密なエネルギーの図は次のように書くべきでしょう。

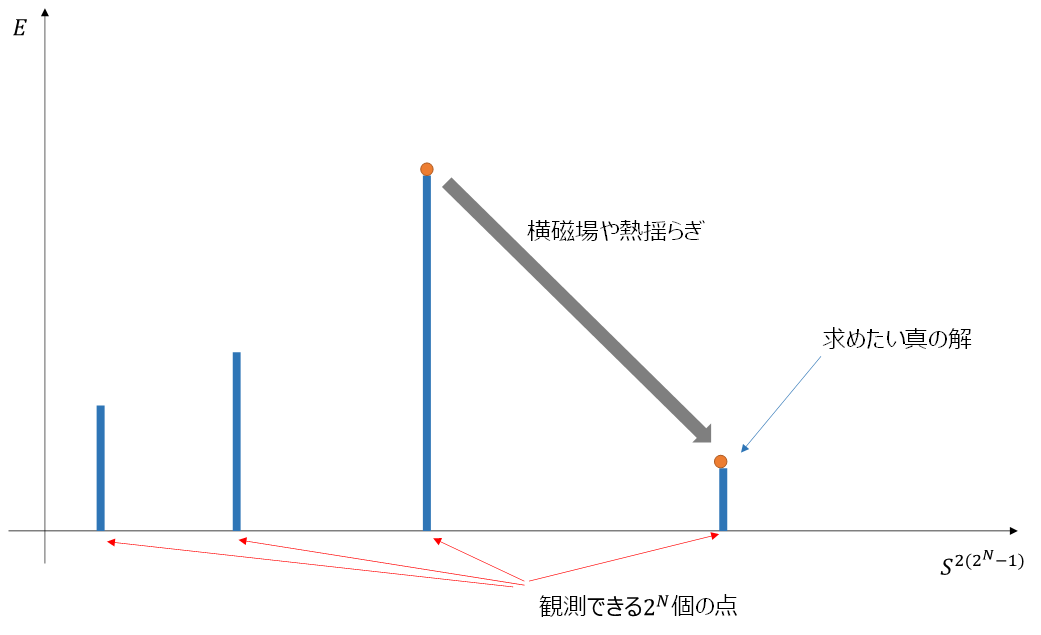
古典計算機ではこの離散的な状態間を横磁場や熱揺らぎによって確率的に移り合うことで解を求めます。
シミュレーテッドアニーリングでは、エネルギーが高いところから低いところへは確率1で遷移、エネルギーが低いところから高いところへはエネルギー差を考慮した確率で遷移するようにします。こうすることで局所解から抜け出せるようにしています。温度を低くしていくことで、エネルギーが低いところから高いところへ遷移する確率は非常に小さくなるので、最後は一つの状態に収束します。
量子モンテカルロ法では、トロッター数分だけ状態を用意し、スピンの配位のエネルギーに加え、トロッターの状態間の相互作用も考慮して状態を遷移します。トロッター数用意したどれかの状態のエネルギーがすごく低くなれば、その状態に向かって収束していきます。複数並行して最低エネルギー状態を探索して、かつ状態間で情報交換しているようなイメージです。

量子アニーリングの場合は状態の重ね合わせを作れるので、離散的な観測可能状態それぞれに確率が与えられます。状態は観測時に確率的に収束します。

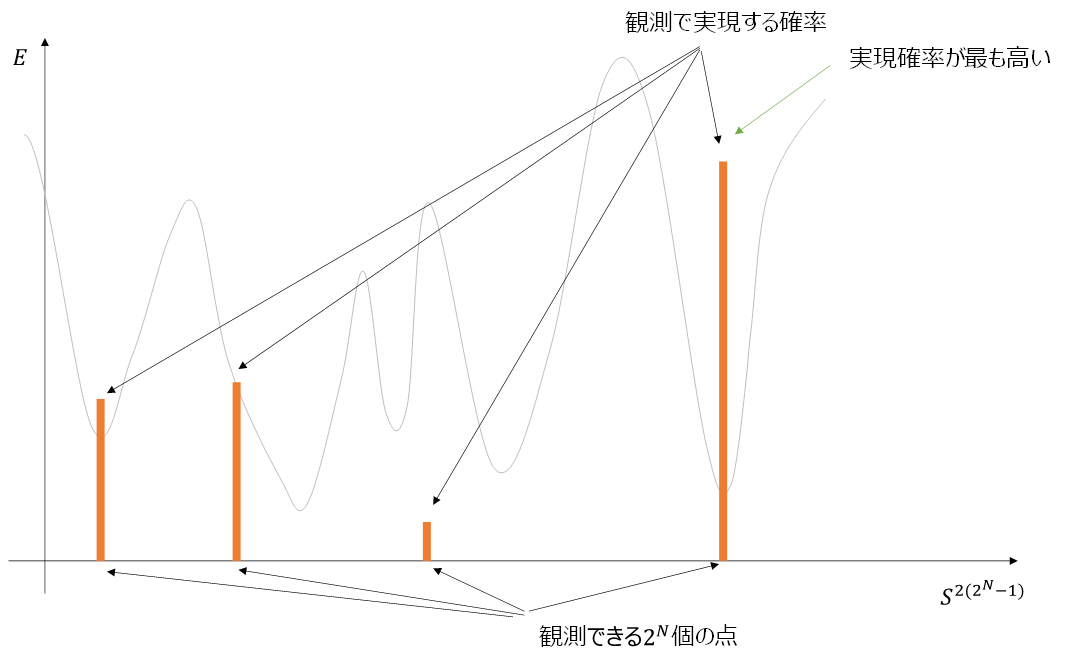
得られる解は確率的なので、1回の観測では解を求められたのかどうか判断できません。何回も計算、観測を繰り返し、図のような棒グラフを作成して、最も実現頻度が高いものを解として採用するのです。IBMが提供しているクラウドの量子コンピューティングは8000回程度の計算、観測を繰り返して答えを求めています。各状態の実現確率が大きく異なる場合は良いのですが、ほとんど差がない場合は、観測で得られた統計にはっきりとした差が現れず、どの解を採用すればよいのかわからなくなってしまいます。したがって計算を設計する際には、求めたい解だけ確率が突出して大きくなるようにする必要があります。

おわりに

量子アニーリングをする際の状態空間のトポロジーについて調べました。