$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
概要
ゲート型量子コンピュータで用いられるアルゴリズムの中に量子フーリエ変換があります。これは離散フーリエ変換を量子コンピュータで実現する方法で、古典コンピュータよりも計算量が少なくて済みます。この記事ではフーリエ変換の意味、計算の仕方、量子ゲートでの実現方法について見ていきたいと思います。
参考
下記サイトを参考にしました。
手順
フーリエ変換
数学的な厳密な話は無しにして、フーリエ変換の意味について簡単に説明します。
そもそもフーリエ変換の前段にフーリエ級数展開があります。まずはフーリエ級数展開について見てみましょう。例として時系列的に変動する連続量があるとします。振動や音がそうです。フーリエ級数展開とは、時間的に周期性を持った複雑な連続量を単純な周期性をもつ関数の和によって表すことです。
イメージを持ってもらうために図を用意しました。下図の左のグラフは複雑な振動に見えます。しかしこのグラフは実は、右のグラフにある周期$1$秒(周波数1Hz)の$\sin$波と周期$1/3$秒(周波数3Hz)の$\cos$波の単純な足し算になっています。
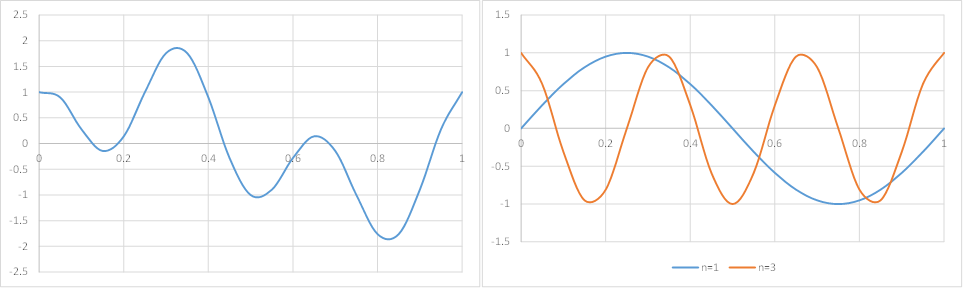
これを数式で表現すると次のように書けます。
f(t) = \sin (2\pi \cdot 1 \cdot t) + \cos(2\pi \cdot 3 \cdot t).
$f(t)$が左図の複雑なグラフの関数です。
より一般に、周期$T$をもつ関数は、基本的な周期を持つ$\sin$波と$\cos$波で分解することができます。
f(t) =\frac{a_0}{2} + \sum_{n=1}^{\infty} \left(a_n \sin \frac{2\pi n t}{T} + b_n \cos \frac{2\pi n t}{T}\right).
右辺の$\sin \frac{2\pi n t}{T}$と$\cos \frac{2\pi n t}{T}$は周期が$T/n$の基本的な波になります。上の例は周期が$T=1$、フーリエ級数が$a_1=1$、$b_3=1$、その他はゼロです。
この式は複素数を用いてより単純な形にできます。
f(t) =\sum_{n=-\infty}^{\infty} c_n \exp \left(\frac{2 \pi i n t}{T}\right).
つまりフーリエ級数展開は、時系列的に(周期的に)変動する連続量にどんな周波数の波が含まれるかを具体的に表したものになります。
そして$f(t)$のフーリエ変換$\tilde f(k)$は、$f(t)$を分解するとどんな周波数の基本的な波を含んでいるか、という情報を表す関数になります。
フーリエ変換の数式は次のようになります。
\tilde f(k) = \int_{-T/2}^{T/2} dt \ f(t) \exp \left( \frac{-2\pi i k t}{T}\right).
上の具体例の$f(t)$をフーリエ変換し、絶対値をとった$|\tilde f (k)|$は次のような図になります。
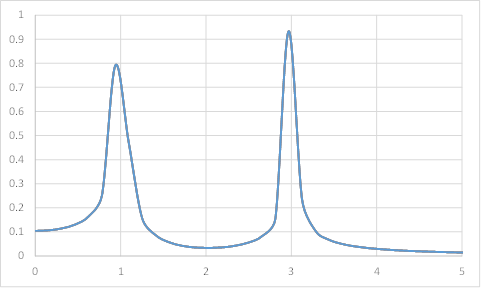
周波数$k=1$Hzと周波数$k=3$Hzのところにピークが立っており、確かに$f(t)$に周期$1$秒(周波数1Hz)の$\sin$波と周期$1/3$秒(周波数3Hz)の$\cos$波が含まれていることがわかります。
フーリエ変換を用いることで、$f(t)$を、$f(t)$に含まれる周波数成分で特徴づけることができるようになります。音の解析や回路の周波数制御など多分野に応用されます。
離散フーリエ変換
コンピュータ上では連続変数があつかえないため、$t$は不連続点$t_j$となり、関数$f(t_j)$は不連続量になります。
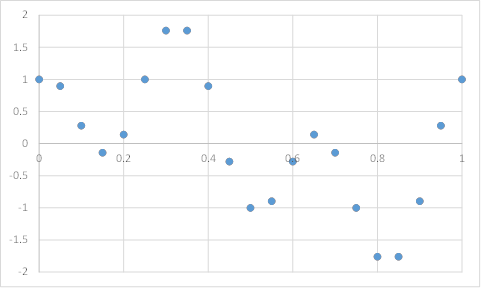
したがってフーリエ変換も離散になります。サンプリング点数は有限個$j=0,1,2...,N-1$として、$f(t_j)=x_j$と書くことにします。これより、振動や音などの時系列データは、ある一定の間隔$\Delta t$でサンプリングした$(x_0,x_1,...)$という列になります。上の具体例の場合は$\Delta t = 0.05$で、$(x_0,x_1,...)$が$(1.000,0.897,0.279,-0.142,...)$となります。
証明はしませんが、離散フーリエ変換は次のような式になります。
y_k =\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} x_j \exp\left(-i \frac{2\pi kj}{N}\right).
ここで$k=0,1,...,N-1$です。フーリエ変換と比べると、連続値が離散値になり、積分が和になっていることがわかります。
さて、これをコンピュータ上に実装することを考えます。$(x_0,x_1,...)^\top$を列ベクトルとみなせば、離散フーリエ変換は行列の演算になっていることがわかります。
\vec y = \frac{1}{\sqrt{N}}W \vec x.
ここで行列$W$の成分は$W_{kj} = \exp\left(-i \frac{2\pi kj}{N}\right)=w^{kj}$です。ここで$w = \exp\left(-i \frac{2\pi}{N}\right)$としました。あとはただの行列計算なので、これでコンピュータ上に実装できそうです。
余談:高速フーリエ変換(fast Fourier transform, FFT)
離散フーリエ変換が力を発揮するのは、$N=2^n$のときです。バタフライ演算というものを用いることで、$2^{n}$のフーリエ変換を$2^{n-1}$のフーリエ変換に落とすことができます。$2^{n-1}$は$2^{n-2}$に、、、と続けていくと、かなり計算量を減らすことができるのです。高速フーリエ変換 - Wikipediaに"N=4"の離散フーリエ変換を"N=2"の離散フーリエ変換に落とす例があるので見てみてください。
このアルゴリズムを用いることで、計算量を$\mathcal O(N^2)$から$\mathcal O(N\log N)$に減らすことができます。
量子フーリエ変換
さて、量子フーリエ変換を考えましょう。量子ビットをうまく利用して、$(x_0,x_1,...)$を$(y_0,y_1,...)$にフーリエ変換することを考えます。
前提として、$N=2^n$とします。天下りになりますが、量子フーリエ変換には$n$量子ビットが必要になります。$1$量子ビットとは、例えば電子のようなスピン1/2をもつ粒子一つを使ったビットです。ブラケット記法で$\ket{r}$とかきます。$r$は0か1をとり、これがスピンのアップ、ダウンに相当します。古典的なビットとの違いは、線形結合$\alpha\ket{0}+\beta\ket{1}$も考えられることです。$\alpha\ket{0}+\beta\ket{1}$は二つのビットの組み合わせではありません。$\alpha\ket{0}+\beta\ket{1}$でひとつのビットを表しています。シュレーディンガーの猫のように、一つの粒子がアップの状態とダウンの状態の重ね合わせになっています。
量子力学のことを知りたい方は、EMANさんのサイトで勉強できます。本格的に学びたい方は「量子力学 I:猪木慶治、川合光」や「現代の量子力学〈上〉J.J.サクライ」をご参照ください。
$n$量子ビットは$\ket{r}$の$n$個のテンソル積$\ket{r_{n-1}}\ket{r_{n-2}}...\ket{r_1}...\ket{r_0}$になります。簡単のために次のような基底をとります。
\ket{j} = \ket{r_{n-1}}\ket{r_{n-2}}...\ket{r_1}...\ket{r_0}.
ここで$j$は、$r_{n-1}...r_0$を二進数と見たときに対応する10進数です。例えばn=2のときは、$N=2^2=4$で、
\ket{0} = \ket{0}\ket{0},\\
\ket{1} = \ket{0}\ket{1},\\
\ket{2} = \ket{1}\ket{0},\\
\ket{3} = \ket{1}\ket{1},
となります。以降ではこの基底を用います。
フーリエ変換後のデータの列$(y_0,y_1,...,y_{N-1})$の基底を量子ビットに取ります。すると、次のように式変形できます。
\begin{align}
\sum_{k=0}^{N-1}y_k\ket{k} &=\sum_{k=0}^{N-1}\sum_{j=0}^{N-1} \frac{1}{\sqrt{N}} x_j \exp\left(-i \frac{2\pi kj}{N}\right)\ket{k} \\
&= \sum_{j=0}^{N-1} x_j \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}\exp\left(-i \frac{2\pi kj}{N}\right)\ket{k}.
\end{align}
この式から、量子ビットに対するフーリエ変換を定義しましょう。
U_{\mathrm{QFT}}\left(\ket{j}\right)=\frac{1}{\sqrt{N}} \sum_{k=0}^{N-1}\exp\left(-i \frac{2\pi kj}{N}\right)\ket{k}.
これを用いることで$y_k$と$x_j$の間に次の関係が成り立ちます。
\sum_{k=0}^{N-1}y_k\ket{k} = U_{\mathrm{QFT}}\left(\sum_{j=0}^{N-1}x_j\ket{j}\right).
フーリエ変換をしたいとき具体的にどうすればいいかというと、まずフーリエ変換したいデータ$(x_0,x_1,...,x_{N-1})$に対し、$\sum_{j=0}^{N-1}x_j\ket{j}$という量子状態を用意します。これにフーリエ変換作用素$U_{\mathrm{QFT}}$を作用させます。すると$\sum_{k=0}^{N-1}y_k\ket{k}$という状態が得られるので、左から$\bra{i}$をかける、つまり基底$i$の射影測定から$y_i$が得られます。この操作を何度も繰り返すことによって$(y_0,y_1,...,y_{N-1})$を得ることができます。
定義から明らかですが、フーリエ変換作用素$U_{\mathrm{QFT}}$は
U_{\mathrm{QFT}} = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}\sum_{k=0}^{N-1}\exp\left(-i \frac{2\pi kj}{N}\right)\ket{k}\bra{j},
とかけます。これで量子フーリエ変換の数学的な構造は以上になります。
量子ゲートによる実装の準備
量子ゲート操作を意識して、フーリエ変換を$n$量子ビットのテンソル積表現で見てみましょう。量子フーリエ変換 (Quantum Fourier Transform) とは - 物理とかを参考にしました。
$\ket{j}$のフーリエ変換は次のように書けました。
\begin{align}
U_{\mathrm{QFT}}\left(\ket{j}\right) &= \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1}\exp\left(-i \frac{2\pi kj}{N}\right)\ket{k} \\
&= \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1}w^{kj}\ket{k}.
\end{align}
ここで$w = \exp\left(-i \frac{2\pi}{N}\right)$です。$\ket{k}$を$n$量子ビットのテンソル積状態に書き換えます。10進数$k$の2進数表示を$s_{n-1}s_{n-2}...s_{0}$とかきます。例えば、$n=3$に対する10進数3は2進数では$011$なので、$s_2=0,s_1=1,s_0=1$です。10進数と2進数の間に次に関係が成り立ちます。
k = \sum_{i=0}^{n-1} s_i \cdot 2^i,
量子状態を
\ket{k}=\ket{s_{n-1}}\ket{s_{n-1}}...\ket{s_0},
と書きます。$k$の和は10進数が$0$から$n-1$まで走るので、これを2進数で表現すると
\sum_{k=0}^{N-1} = \sum_{s_{n-1}=0}^{1}\sum_{s_{n-2}=0}^{1}...\sum_{s_{0}=0}^{1},
となります。また、$N=2^n$です。これを用いると次のようになります。
\begin{align}
U_{\mathrm{QFT}}\left(\ket{j}\right)
& = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{N-1}w^{kj}\ket{k} \\
& = \frac{1}{\sqrt{2^n}} \sum_{s_{n-1}=0}^{1}\sum_{s_{n-2}=0}^{1}...\sum_{s_{0}=0}^{1} w^{j\cdot \sum_{i=0}^{n-1} s_i \cdot 2^i}\ket{s_{n-1}}\ket{s_{n-1}}...\ket{s_0}\\
& = \frac{1}{\sqrt{2^n}} \sum_{s_{n-1}=0}^{1}\sum_{s_{n-2}=0}^{1}...\sum_{s_{0}=0}^{1} \left(\prod_{i=0}^{n-1}w^{j\cdot s_i \cdot 2^i}\right)\ket{s_{n-1}}\ket{s_{n-1}}...\ket{s_0} \\
& = \frac{1}{\sqrt{2^n}} \left(\prod_{i=n-1}^{0} \sum_{s_{i}=0}^{1}w^{j\cdot s_i \cdot 2^i}\ket{s_{i}}\right)\\
& = \frac{1}{\sqrt{2^n}} \prod_{i=n-1}^{0} \left(\ket{0} + w^{j\cdot 2^i}\ket{1}\right)\\
&=\frac{1}{\sqrt{2^n}}\left(\ket{0}+w^{2^{n-1}\cdot j}\ket{1}\right)\left(\ket{0}+w^{2^{n-2}\cdot j}\ket{1}\right)...\Big(\ket{0}+w^{1\cdot j}\ket{1})\Big).
\end{align}
ここで$\prod_{i=n-1}^{0}$は$i$を$n-1,n-2,...,1,0$の順で積をとる総乗です。
さらに10進数$j$を2進数表現にしましょう。$j$の2進数表現を$r_{n-1}r_{n-2}...r_{1}r_0$と書くと、
j = \sum_{l=0}^{n-1} r_l \cdot 2^l,
と表されます。$w = \exp\left(-i \frac{2\pi}{N}\right) = \exp\left(-i \frac{2\pi}{2^n}\right)$であることを用いると、さらに式変形を続けて、
\begin{align}
U_{\mathrm{QFT}}\left(\ket{j}\right)
& = \frac{1}{\sqrt{2^n}} \prod_{i=n-1}^{0}\left( \ket{0} + w^{j\cdot 2^i}\ket{1}\right)\\
& = \frac{1}{\sqrt{2^n}} \prod_{i=n-1}^{0}\left( \ket{0} + w^{ 2^i\cdot \sum_{l=0}^{n-1} r_l \cdot 2^l}\ket{1}\right)\\
& = \frac{1}{\sqrt{2^n}} \prod_{i=n-1}^{0}\left( \ket{0} + \left(\prod_{l=0}^{n-1}w^{ r_l\cdot 2^{i+l} }\right)\ket{1}\right)\\
& = \frac{1}{\sqrt{2^n}} \prod_{i=n-1}^{0}\left( \ket{0} + \left(\prod_{l=0}^{n-1}\exp(-i 2\pi r_l\cdot 2^{i+l-n})\right)\ket{1}\right)\\
& = \frac{1}{\sqrt{2^n}} \prod_{i=n-1}^{0}\left( \ket{0} + \left(\prod_{l=0}^{n-1}\exp(-i 2\pi r_l\cdot 2^{l-(n-i)})\right)\ket{1}\right)\\
& = \frac{1}{\sqrt{2^n}} \prod_{i=n-1}^{0}\left( \ket{0} + \left(\prod_{l=0}^{n-1-i}\exp(-i 2\pi r_l\cdot 2^{l-(n-i)})\right)\ket{1}\right).
\end{align}
最後の行は$l-(n-i)<0$でないと$\exp(-i 2\pi r_l\cdot 2^{l-(n-i)})=1$となってしまうことから総乗の範囲を小さくしました。
\begin{align}
U_{\mathrm{QFT}}\left(\ket{r_{n-1}}\ket{r_{n-2}}...\ket{{r_0}}\right)
& = \frac{1}{\sqrt{2^n}} \prod_{i=n-1}^{0}\left( \ket{0} + \left(\prod_{l=0}^{n-1-i}\exp(-i 2\pi r_l\cdot 2^{l-(n-i)})\right)\ket{1}\right)\\
& = \frac{1}{\sqrt{2^n}} \left( \ket{0} + e^{-i 2\pi r_0\cdot 2^{-1} } \ket{1}\right)\left( \ket{0} + e^{-i 2\pi r_0\cdot 2^{-2} } e^{-i 2\pi r_1\cdot 2^{-1} } \ket{1}\right)...\left( \ket{0} + \prod_{l=0}^{n-1}e^{-i2\pi r_l\cdot2^{l-n}} \ket{1}\right).
\end{align}
次のような記号を導入します。
0.r_{n-1}r_{n-2}...r_{0}=r_{n-1}2^{-1}+r_{n-2}2^{-2}+...+r_{0}2^{-n}.
これは2進小数の表記になっているとわかります。すると次のようにまとめて書くことができます。
\begin{align}
U_{\mathrm{QFT}}\left(\ket{r_{n-1}}\ket{r_{n-2}}...\ket{{r_0}}\right)
& = \frac{1}{\sqrt{2^n}} \prod_{l=1}^{n}\Big( \ket{0} + \exp(-i 2\pi \cdot 0.r_{l-1} ...r_0 )\ket{1}\Big).
\end{align}
ただ、個人的にはこの書き方はなじみがなくわかりにくいため、公式として覚える際の記号と思っておけばよいと思います。
以上でフーリエ変換作用素が量子ビットをどのように変換するのかわかりました。次の節はフーリエ変換を具体的に実装するためのゲート演算を考えます。これによって計算量がわかります。
量子ゲート操作
フーリエ変換作用素のほうを考えます。実はアダマールゲートと位相回転ゲートを用意すれば作用素は書けます。
天下り的なのですが、$\ket{r_{m-1}}$を次の量子状態に変換する操作を考えます。
\begin{align}
&\frac{1}{\sqrt{2}}\left(\ket{0} +
\exp(-i 2\pi \cdot 0.r_{m-1} ...r_0 )\ket{1}\right) \\
= &\frac{1}{\sqrt{2}}\left(\ket{0} + \exp(-i 2\pi r_0\cdot 2^{-m} )\exp(-i 2\pi r_1\cdot 2^{-m+1} )...\exp(-i 2\pi r_{m-2}\cdot 2^{-2} )\exp(-i 2\pi r_{m-1}\cdot 2^{-1} )\ket{1}\right) .
\end{align}
$\ket{r_{m-1}}$にアダマールゲート、
\begin{align}
H =\frac{\ket{0} + \ket{1}}{\sqrt{2}}\bra{0} + \frac{\ket{0} - \ket{1}}{\sqrt{2}} \bra{1},
\end{align}
を作用させると、次の式が得られます。
\begin{align}
H \ket{r_{m-1}} = \frac{1}{\sqrt{2}}\left(\ket{0} + \exp(-i 2\pi r_{m-1}\cdot 2^{-1} )\ket{1}\right) .
\end{align}
$r_{m-1}$が$0$の場合と$1$の場合で考えればすぐにわかります。
残りは$\ket{0}$にかかる位相です。例えば$\exp(-i 2\pi r_{m-2}\cdot 2^{-2} )$を考えましょう。これは$r_{m-2}=0$のときは$1$をかけ、$r_{m-2}=1$のときは$\exp(-i 2\pi \cdot 2^{-2} )$をかけます。このように他のビットの値に応じて演算が変わる場合、制御ゲートというものを用います。例えばですが、今量子ビットが2ビット$\ket{r_{m-1}}\ket{r_{m-2}}$と並んでいるとします。これに対して行う制御ゲートの演算は
\begin{align}
V = I \otimes \ket{0}\bra{0} + \left( \ket{0}\bra{0} + \exp(-i 2\pi \cdot 2^{-2})\ket{1}\bra{1} \right) \otimes \ket{1}\bra{1},
\end{align}
となります。$\ket{r_{m-2}}$が$\ket{0}$のときは$\ket{r_{m-1}}$に高等演算を、$\ket{r_{m-2}}$が$\ket{1}$のときは$\ket{r_{m-1}}$の$\ket{1}$だけが位相回転する演算になっていることがわかります。同様にして他の位相回転も作ることができます。
例えば2量子ビットの場合のゲート演算は次のようになります。
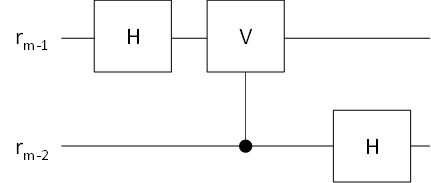
ここで制御元は、初期値をもとに制御するので、制御元を先にアダマール変換してしまわないよう順番に注意しましょう。
以上の演算を$\ket{r_{n-1}}\ket{r_{n-2}}...\ket{{r_0}}$に用いると
\begin{align}
\ket{r_{n-1}}\ket{r_{n-2}}...\ket{{r_0}} \rightarrow \ \frac{1}{\sqrt{2^n}} \prod_{l=n}^{1}\Big( \ket{0} + \exp(-i 2\pi \cdot 0.r_{l-1} ...r_0 )\ket{1}\Big),
\end{align}
となります。これで量子フーリエ変換ができた、、、と思ったら、よく見てみてみると積の順番が求めたいものとは逆になっています!
安心してください。量子演算には二つのビットを入れ替える演算が存在します。これを交換ゲートといいます。交換ゲートはCNOTゲート三つで構成されます。
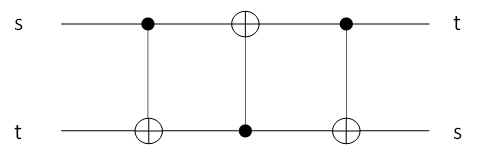
これを用いて、順番を入れ替えれば量子フーリエ変換と一致するので、これにてゲート演算ができたことになります。
さて、計算量ですが、各ビットに対しアダマール変換と位相変換を施しますので、これのゲート数が
\begin{align}
\sum_{k=1}^n (k+1) = \frac{1}{2}n(n+1)
\end{align}
となります。最後の交換ゲートは$3\times [n/2]$個必要になります。ここで$[]$はガウス記号です。よって計算量は$\mathcal O(n^2)=\mathcal O((\log N)^2)$となります。高速フーリエ変換が$\mathcal O(N\log N)$だったので、量子コンピュータのほうが計算量が少なくて済むことがわかりますね。
さいごに
以上を通してフーリエ変換の意味、計算の仕方、量子ゲートでの実現方法を見てきました。そして量子コンピュータのほうが計算量が少なくて済むことも見ることができました。
しかし、上でも述べたように、量子コンピュータから計算結果を取り出すには、計算、測定、計算、測定、、、と何度も繰り返し行う必要があります。このことを考慮すると、結局指数時間かかってしまうと考えられており、あまりフーリエ変換自体を量子コンピュータで行う意味はありません。
Shorのアルゴリズムなど、量子フーリエ変換を他のアルゴリズムの一部として用いるほうが実用的のようです。