はじめに
簡単のために二値分類に限定します。
機械学習などを利用した分類器において、分類の精度を評価する方法の一つに混同行列というものがあります。あるデータに対する予測結果(正例、負例)と実際の値供(正例、負例)の組み合わせは2×2で次の4つに分類されます。
- 真陽性(TP: true positive):実際の正例のうち正例と予測できた件数
- 偽陽性(FP: false positive):実際は負例のうち正例と予測されてしまった件数
- 真陰性(TN: true negative):実際の負例のうち正例と予測できた件数
- 偽陰性(FN: false negative):実際の正例のうち負例と予測されてしまった件数
これを行列で表示すると下記のようになります。
| 正例(予測) | 負例(予測) | |
|---|---|---|
| 正例(実績) | True positive(TP) | False negative(FN) |
| 負例(実績) | False positive(FP) | True negative(TN) |
この4パターンそれぞれの件数から、分類器を評価する指標をつくることができます。
正解率(Accuracy)
全体の予測のうち、正しい予測ができた件数を表します。
\mathrm{ACC} = \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}
逆に$\mathrm{ERR} = 1 - \mathrm{ACC}$を誤分類率といいます。
真陽性率(True positive rate)
別名を再現率 (Recall)といいます。実際の正例のうち正例と予測できた割合を表します。
\mathrm{TPR} = \mathrm{REC} = \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}
偽陽性率(False positive rate)
実際の負例のうち正例と予測されてしまった割合を表します。
\mathrm{FPR} = \frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN}}
適合率 (Precision)
正例と予測したうち実際に正例であった割合を表します。
\mathrm{PRE} = \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}
F1スコア (F1-score)
適合率と再現率の調和平均を表します。
\mathrm{F1} = \frac{2\times \mathrm{PRE}\times \mathrm{REC}}{\mathrm{PRE}+\mathrm{REC}}
理想的な分類器はFPとFNがゼロとなる分類器です。しかし、実際は完全な分類はできません。完全な分類ができたとしたら、それは自明な分類問題か、教師データに過学習していることが疑われます。
ところで、識別モデルの分類器では、予測対象がどちらに分類されるか、確率を求めることが出来ます。分類をする単純な方法としては確率が大きい方、すなわち確率が0.5より大きい方に分類すればよいのですが、この分類の境界を調整することでTPRとFPRを調整することが出来ます。正例の方に予測しやすくすると、実際の正例を正しく予測しやすくなる一方、実際の負例を正例と誤って予測しやすくなってしまいます。一方、実際の負例を正例と予測しないようにすると、実際の正例を正しく予測するのが難しくなります。分類の境界を動かしたときに、TPRとFPRがどのように変化するかを表すのがROC曲線です。
ROC曲線(Receiver Operating Characteristic curve、受信者動作特性曲線)とは、縦軸に真陽性率(TPR: true positive rate)、横軸に偽陽性率(FPR: false positive rate)の値をプロットした曲線です。予測確率を予測ラベルに変換する際の閾値を0.0と1.0の間で徐々に変化させ、真陽性率と偽陽性率の関係をプロットすることでROC曲線を描けます。
乳癌のデータを使用してROC曲線をプロットしてみましょう。
環境
- MacOS Mojave 10.14.2
- scikit-learn==0.19.1
参考
- [第2版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズ(https://www.amazon.co.jp/dp/B07BF5QZ41/ref=dp-kindle-redirect?_encoding=UTF8&btkr=1)
手順
予測
乳癌のデータを使用します。乳癌が「悪性腫瘍」か「良性腫瘍」かを分類します。model.predict_proba()で分類の確率を取得します。戻り値は0と1の予測それぞれの確率となるので、1の方の確率のみy_predに取得します。
from sklearn.datasets import load_breast_cancer
from sklearn import svm
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, test_size=0.5, random_state=0)
model = svm.SVC(kernel='linear', probability=True, random_state=0)
model.fit(X_train, y_train)
y_pred = model.predict_proba(X_test)[:,1]
AUCの算出とROC曲線の描画
roc_curve()で境界値およびFPR、TPRを算出します。
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
# AUCの算出
fpr, tpr, thresholds = roc_curve(y_test, y_pred)
roc_auc = auc(fpr, tpr)
# ROC曲線の描画
plt.plot(fpr, tpr, color='red', label='ROC curve (area = %.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="best")
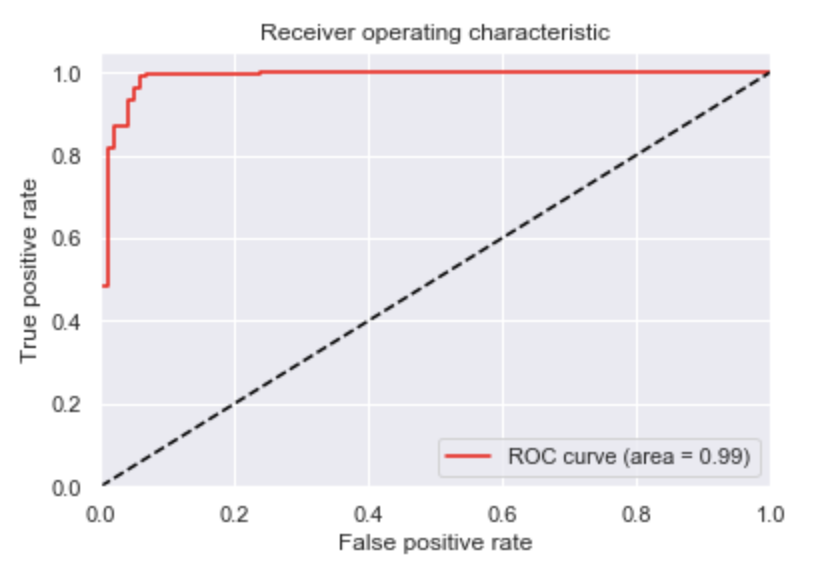
境界値を変えていくとFPRが上がっていくにつれてTPRも上がっていきます。FPRが小さく、かつTPRが十分大きい境界が存在すれば良いモデルと言えるので、ROC曲線を積分した値、すなわちAUC(area under the curve、ROC曲線下面積)が1に近いほど良いモデルと言えます。auc()にroc_curve()で求めたFPR、TPRを代入することで求めることが出来ます。
このモデルはAUCが0.99と1に近いので高い性能を有したモデルであると言えます。
混同行列
境界値Pのもとでの混同行列は下記のように出力できます。
from sklearn.metrics import confusion_matrix
P = 0.4
y_pred = (y_pred > P).astype(int)
m = confusion_matrix(y_test, y_pred)
print('Confution matrix:\n{}'.format(m))
# 出力------------
# Confution matrix:
# [[ 94 7]
# [ 1 183]]
各指標もscikit-learnで出力することができます。
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print('正解率:{:.3f}'.format(accuracy_score(y_test, y_pred)))
print('適合率:{:.3f}'.format(precision_score(y_test, y_pred)))
print('再現率:{:.3f}'.format(recall_score(y_test, y_pred)))
print('F1値:{:.3f}'.format(f1_score(y_test, y_pred)))
# 出力------------
# 正解率:0.972
# 適合率:0.963
# 再現率:0.995
# F1値:0.979
おわりに
乳癌のデータを用いてROC曲線について見てきました。教師データの分割によってROC曲線は変化するので、クロスバリデーションとともにROC曲線を求め、ROC曲線を平均した曲線も評価に使用されます。詳細は参考をご覧ください。