[論文]SSD: Single Shot MultiBox Detector

Info

• タイトル：SSD: Single Shot MultiBox Detector
• カンファ：ECCV2016
• 著者：Wei Liu, Dragomir Anguelov, Dumitru Erhan, Christian Szegedy, Scott Reed, Cheng-Yang Fu, Alexander C. Berg
• 論文：https://arxiv.org/abs/1512.02325
• プロジェクトページ：https://github.com/weiliu89/caffe/tree/ssd

概要

• 単一のディープニューラルネットワークを用いて画像中のオブジェクトを検出する方法を提示する。
• SSDと名付けられた我々のアプローチは、バウンディングボックスの出力空間を、特徴マップの位置ごとに異なるアスペクト比とスケールにわたるデフォルトボックスの集合に離散化する。
• 予測時に、ネットワークは各デフォルトボックスにおける各オブジェクトカテゴリの存在に対するスコアを生成し、オブジェクトの形状によりよく一致するようにボックスを調整する。
• また、解像度の異なる複数の特徴マップを組み合わせて予測することで、様々な大きさの物体を自然に扱うことができる。
• PASCAL VOC、COCO、ILSVRCの各データセットを用いた実験の結果、SSDは、学習と推論の両方に統一されたフレームワークを提供しながら、追加の物体提案段階を利用する手法と同等の精度を持ち、より高速であることが確認された。
• 300×300の入力に対して、SSDはVOC2007テストにおいて74.3%のmAPを達成し、Nvidia Titan Xを用いた59 FPSで、512×512の入力に対して、SSDはFaster R-CNNモデルよりも優れた76.9%のmAPを達成した。
• SSDは、他のシングルステージ手法と比較して、入力画像サイズが小さい場合でも、はるかに優れた精度を実現する。

背景

• Region Proposal Networkと分類器を組み合わせたパイプラインによるアプローチは正確ではあるものの、組み込みシステムには計算量が多すぎ、ハイエンドのハードウェアを使用した場合でも、リアルタイムアプリケーションには遅すぎる。
• 最も高速な高精度検出器であるFaster R-CNNでさえ、わずか7フレーム/秒（FPS）で動作している。
• 本論文では、RPNと分類器に分かれない、エンドツーエンドのオブジェクト検出器を導入する。
• 結果、高精度を保ちつつ速度が大幅に改善された（VOC2007テストにおいて、AP74.3%で59FPS;Faster R-CNN はでmAP 73.2% で7FPS　、YOLO は mAP 63.4%で45 FPS）。

本論文の貢献は以下のようにまとめられる。

• SSDは、複数カテゴリのシングルショット検出器であり、従来のシングルショット検出器の最先端技術（YOLO）よりも高速であり、かつ著しく高精度であり、実際、明示的な領域提案とプーリングを行う低速な技術（Faster R-CNNを含む）と同程度の高精度であることを示す。
• SSDの中核は、特徴マップに適用される小さな畳み込みフィルタを用いて、デフォルトの境界ボックスの固定セットについて、カテゴリスコアとボックスオフセットを予測することである。
• 高い検出精度を達成するために、異なるスケールの特徴マップから異なるスケールの予測値を生成し、アスペクト比によって予測値を明示的に分離している。
• これらの設計上の特徴により、低解像度の入力画像であっても、シンプルなエンドツーエンドの学習と高精度を実現し、速度と精度のトレードオフをさらに改善する。
• 実験では、PASCAL VOC、COCO、ILSVRCで評価した様々な入力サイズのモデルについて、タイミングと精度の分析を行い、最近の様々な最先端アプローチと比較している。

手法

ネットワーク

ベースネットワークの各層から、それぞれの畳み込み特徴層を通して最終特徴を形成する。ベースネットワークはレイヤーを通るごとに特徴マップのサイズが小さくなるので、複数の解像度の予測を可能にする。

畳み込み特徴層の出力は、デフォルトボックスに対するカテゴリのスコア、デフォルトボックス座標に対する形状オフセットである。

ここで、デフォルトボックスを説明する。まず、下図の(b)および(c)のマス目がアンカーボックスに相当する特徴マップのピクセルである。畳み込み層を通ってそれぞれ$8\times8$と$4\times4$サイズになった特徴マップの各ピクセルを、元の画像の解像度に引き戻した時のボックスがアンカーボックスである。つまり特徴マップが$m\times n$サイズなら、アンカーボックスは$mn$個ある。

各アンカーボックスに対して、スケールやアスペクト比を変えた$k$個のボックスを作成する。下図の点線で表されるボックスである。これがデフォルトボックスである。したがってデフォルトボックスは1つの特徴マップにつき$kmn$個ある。全特徴マップを合わせて、論文の設定では8732個のデフォルトボックスが存在する。

• Conv4_3: 38 * 38 * 4 = 5776
• Conv7: 19 * 19 * 6 = 2166
• Conv8_2: 10 * 10 * 6 = 600
• Conv9_2: 5 * 5 * 6 = 150
• Conv10_2: 3 * 3 * 4 = 36
• Conv11_2: 4
• Total: 5776+ 2166 + 600 + 150 + 36 + 4 = 8732

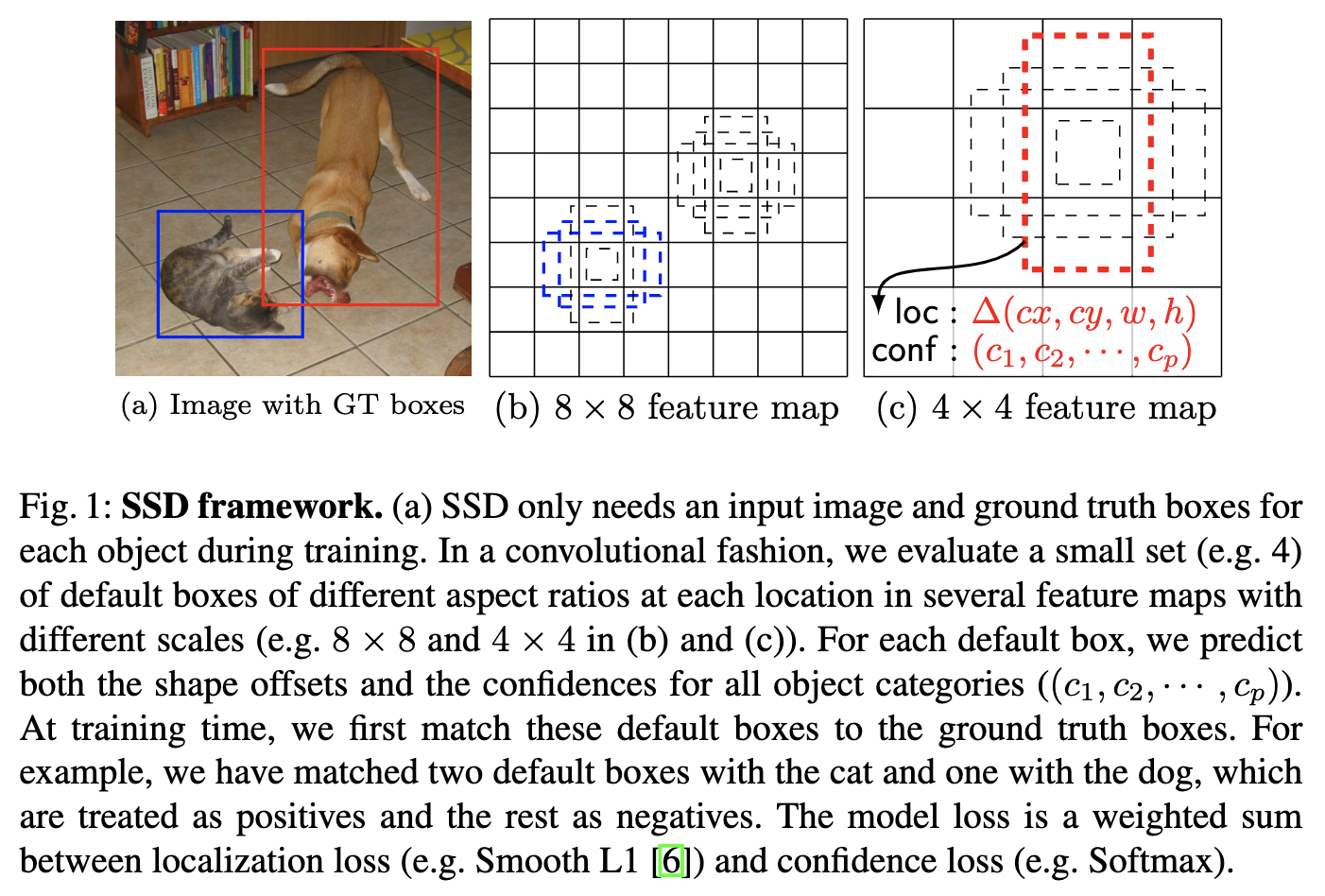
モデルは、各デフォルトボックスとグランドトゥルースのずれ、すなわちオフセットを予測して、完全なボックスを予測する。

\begin{aligned}
cx &= cx_d(1+0.1\Delta cx) \\
cy &= cy_d(1+0.1\Delta cy) \\
w &= w_d e^{0.2\Delta w} \\
h &= h_d e^{0.2\Delta h} \\
\end{aligned}

添字$d$がついているものがデフォルトボックスの値で、$\Delta$がついているものがオフセットである。モデルはオフセット$(\Delta cx, \Delta cy, \Delta w, \Delta h)$を出力する。また、同時にデフォルトボックスに対してクラス確率$(c_1, c_2, \cdots, c_p)$を出力する。$p$はクラス数である。

したがって、1つの特徴マップから出力されるテンソルの形状は$M\times N \times K \times (p+4)$である。

損失関数

学習時は、グランドトゥルースボックスとjaccard係数が0.5以上になるデフォルトボックスを紐付ける。

損失関数を次のように与える。

\begin{aligned}
L(x,c,l,g) &= \frac{1}{N}\left( L_{\mathrm{conf}}(x,c) + \alpha L_{\mathrm{loc}}(x,l,g) \right)
\end{aligned}

$N$はグランドトゥルースボックスに紐付いたデフォルトボックスの数。$N=0$のときは$L=0$とする。$\alpha$は論文では交差検証の結果$1$にした。

$l$を予測ボックス、$g$をグランドトゥルースボックス、$d$をデフォルトボックスに関連する数値とし、具体的に何を表すかは添字$\mathrm{(cx, cy, w, h)}$で表すとする。

位置に関する損失は次のようになる。

\begin{aligned}
L_{\mathrm{loc}}(x,l,g)
&= \sum_{k=1}^p\sum_{i\in \mathrm{Default Box}}\sum_{j\in \mathrm{GT Box}} \sum_{m\in (cx, cy, w, h)} x_{ij}^k \mathrm{smooth}_{\mathrm{L1}}(l_i^m- \hat g_j^m) \\
\hat g_j^{\mathrm{cx}} &= \frac{g_j^{\mathrm{cx}} - d_i^{\mathrm{cx}}}{d_i^{\mathrm y}} \\
\hat g_j^{\mathrm{cy}} &= \frac{g_j^{\mathrm{cy}} - d_i^{\mathrm{cy}}}{d_i^{\mathrm h}} \\
\hat g_j^{\mathrm w} &= \log \frac{g_j^{\mathrm w} }{d_i^{\mathrm w} } \\
\hat g_j^{\mathrm h} &= \log \frac{g_j^{\mathrm h} }{d_i^{\mathrm h} }
\end{aligned}

ここで、$x_{ij}^k$は、クラス$k$のデフォルトボックス$i$とクラス$k$のグランドトゥルースボックス$j$が紐付いているときに$1$で、それ以外のときは$0$となる指示関数である。また、下4つの式は、項に$x_{ij}^k$があることを前提に成り立つ式で、厳密には正しい表記ではないことに注意（が、意味は伝わると思って略記した）。

クラスの信頼度に関する損失は次のようになる。

\begin{aligned}
L_{\mathrm{conf}}(x,c) &=
-\sum_{k=1}^p\sum_{i\in \mathrm{Default Box}}\sum_{j\in \mathrm{GT Box}}  x_{ij}^k \log(\hat c_i^k) - \sum_{i\in \mathrm{Default Box}}\log(\hat c_i^0)\prod_{k=1}^p\prod_{j\in \mathrm{GT Box}}(1-x_{ij}^k ) \\
\hat c_i^k &= \frac{\exp(c_i^k)}{\sum_k \exp(c_i^k)}
\end{aligned}

デフォルトボックスのパラメータ

特定の特徴マップが物体の特定のスケールに反応するように学習するようにする。例えば、$m$ 個の特徴マップを予測に使いたいとする。各特徴マップのデフォルトボックスのスケールは次のように計算される。

s_k = s_{\mathrm{min}} + \frac{s_{\mathrm{max}} - s_{\mathrm{min}}
}{m-1}(k-1), \ k \in [1,m]

ここで、$s_{\mathrm{min}}=0.2$であり、$s_{\mathrm{max}}=0.9$ である。デフォルトボックス　に対して異なるアスペクト比を、$a_r\in{1, 2, 3, 1/2 , 1/3 }$とする。各デフォルト・ボックスの幅$(w^a_k = s_k \sqrt{a_r} ）$と高さ$（h^a_k = s_k/\sqrt a_r ）$を計算することができる。アスペクト比が1の場合、スケールが$s_k'=\sqrt{s_k s_{k+1}}$のデフォルトボックスも追加され、1つの特徴マップのピクセルあたり6個のデフォルトボックスができることになる。

各デフォルトボックスの中心を$(i+0.5)/|f_k|, (j+0.5)/|f_k|)$とする。ここで |f_k| はk番目の正方形特徴マップのサイズ、 $i, j\in [0, |f_k|]$ とする。実際には、特定のデータセットに最も適合するようにデフォルトボックスの分布を設計することも可能である。最適なタイリングをどのように設計するかは、同様に未解決の問題である。

多くの特徴マップの全ての位置から、異なるスケールとアスペクト比を持つ全てのデフォルトボックスの予測値を組み合わせることで、様々な入力オブジェクトのサイズと形状をカバーする、多様な予測値のセットを持つことができる。4 × 4 の特徴マップのデフォルトボックスには犬がマッチングするが、8 × 8 の特徴マップのデフォルトボックスにはマッチングしない。これは、これらのボックスは縮尺が異なり、犬のボックスと一致しないため、学習時にネガティブとみなされるためである。

Hard negative mining

デフォルトボックスのほとんどはネガティブになる。これは、正例と負例の学習例間に著しい不均衡をもたらす。そこで、全てのネガティブな学習例を使用するのではなく、各デフォルトボックスの信頼度の損失が最も大きい学習例を用いてソートし、ネガティブとポジティブの比率が最大で3:1になるように上位の学習例を選択する。これにより、最適化が高速化され、より安定した学習が可能になることがわかった。

Data augmentation

• オリジナルの入力画像全体を使用する。

• オブジェクトとの最小のjaccardオーバーラップが0.1、0.3、0.5、0.7、または0.9となるようにパッチをサンプリングする。

• ランダムにパッチをサンプリングする。

各パッチのサイズは元画像の[0.1, 1]であり，アスペクト比は1/2から2の間である。グランドトゥルースボックスの中心がサンプリングされたパッチ内にある場合，その重なり部分を保持する。前述したサンプリングの後、各パッチは固定サイズにリサイズされ、0.5の確率で水平に反転される。

評価

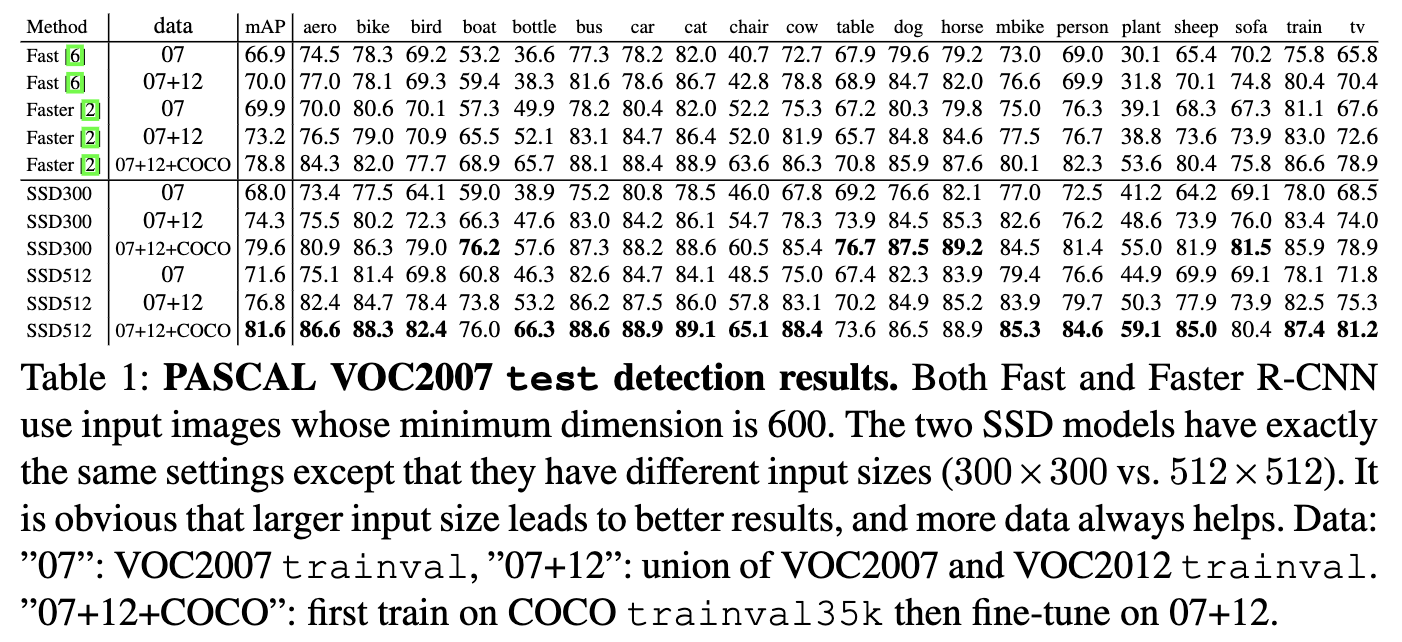
• PASCALではFaster-RCNNよりも精度が高い。

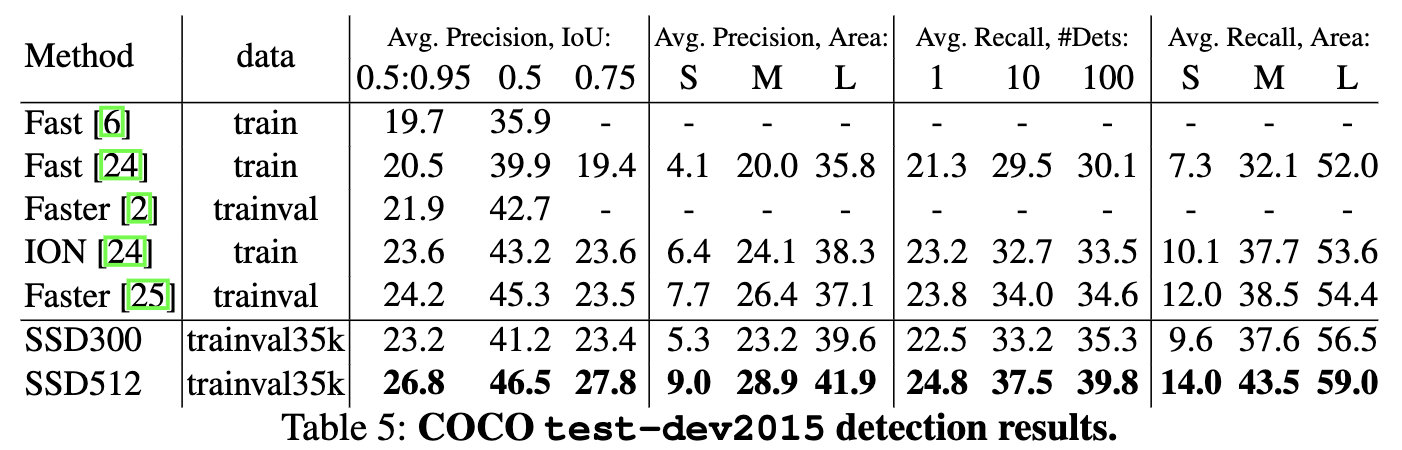
※なぜか条件を揃えて実験しない。

SSDの大きな貢献は、異なる出力レイヤーに異なるスケールのデフォルトボックスを使用することである。この優位性を測定するために、レイヤーを徐々に削除し、結果を比較する。公平に比較するために、レイヤーを削除するたびに、ボックスの総数がオリジナル（8732個）と同じになるようにデフォルトボックスのタイリングを調整する。これは、残ったレイヤーに、より多くのスケールのボックスを積み重ね、必要に応じてボックスのスケールを調整することによって行われる。

層数が少なくなると精度が低下し、74.3から62.4まで単調に低下していることを示している。

複数のスケールのボックスを1つのレイヤーに重ねる場合、多くは画像境界上にあるため、慎重に扱う必要がある。そこで、Faster R-CNNで用いられている、境界上にあるボックスを無視する戦略を試してみた。その結果、いくつかの興味深い傾向が見られた。例えば、非常に粗い特徴マップ（conv11_2 (1 × 1) や conv10_2 (3 × 3) など）を用いると、性能が大きく損なわれる．これは、枝刈り後の大きな物体をカバーするための大きなボックスが足りなくなるためと思われる。また、より細かい解像度のマップを中心に使用すると、プルーニング後も十分な数のラージボックスが残るため、再び性能が向上し始める。また、conv7のみを用いて予測した場合、性能は最悪となり、異なるスケールのボックスを異なるレイヤーに分散させることが重要であるというメッセージが強くなった。

さらに、ROIプーリングに依存しないため、低解像度の特徴マップにおけるビンの崩壊問題は発生しない。

※他の検証もあるが、省略。

まとめ・感想

• Faster-RCNNはRPNを使用して提案を作成するが、手動で大量の提案を作成しても十分性能が出ることを示した。
• 複数のスケールで特徴を抽出していることが重要。
• オブジェクトネスの予測がないため、グランドトゥルースのアノテーションがしやすい。