はじめに
かの有名なアヤメのデータセット1を使用して、2標本の母平均の差の検定を行います。データセットはscikit-learnのライブラリから読み込むことができます。
検定の手順は次の3つです。
データが正規分布に従うか検定
統計的仮説検定を行う場合、データが正規分布に従うことを前提としているため、データが正規分布に従うか確かめる必要があります。2標本の母分散が等しいか検定
2標本の母平均の差の検定は、2標本の分散が等しいかで手法が変わるため、母分散の検定を行います。2標本の母平均が等しいか検定
最後に母平均が等しいか検定します。
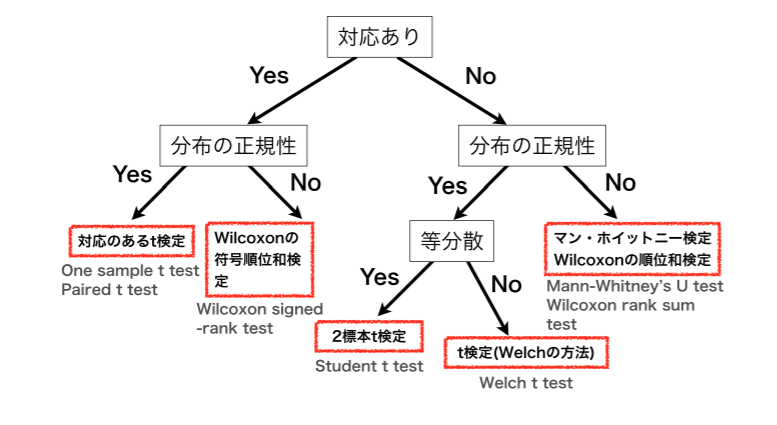
下記はより一般の2標本の平均に関する検定の手順です。2
環境
- python 3.6
- scikit-learn 0.19.1
- pandas 0.23.4
参考
- scikit-learnのアヤメのデータセットについて 『5. Dataset loading utilities scikit-learn 0.20.1 documentation』(https://scikit-learn.org/stable/datasets/index.html
手順
データ準備
アヤメのデータを読み込みます。scikit-learnのデータセットライブラリにはいくつか練習用のデータセットが格納されています。
from sklearn.datasets import load_iris
# アヤメの花
iris = load_iris()
このデータには3種類のアヤメのデータが入っています。アヤメのデータはクラス分類に使用されるデータで、targetというのがラベルを表しています。
iris.target_names
# array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
iris.targetにアヤメの種類のラベルが入っていますが、数値で入っています。ラベルとアヤメの種類の関係は下記の表のとおりです。
| アヤメの種類 | 番号 |
|---|---|
| setosa | 0 |
| versicolor | 1 |
| virginica | 2 |
次に特徴量ですが、特徴量は4種類あります。
iris.feature_names
# ['sepal length (cm)',
# 'sepal width (cm)',
# 'petal length (cm)',
# 'petal width (cm)']
これはがく片(sepal)と花弁(petal)の大きさを表しています。このサイトにアヤメの写真が掲載されています。

今回の目的はsetosaとversicolorのそれぞれのsepal length (cm)について、その平均に差があるか検定することです。
データはarray型で格納されています。
iris.data
# array([[ 5.1, 3.5, 1.4, 0.2],
# [ 4.9, 3. , 1.4, 0.2],
# [ 4.7, 3.2, 1.3, 0.2],
# [ 4.6, 3.1, 1.5, 0.2],
# 以下略
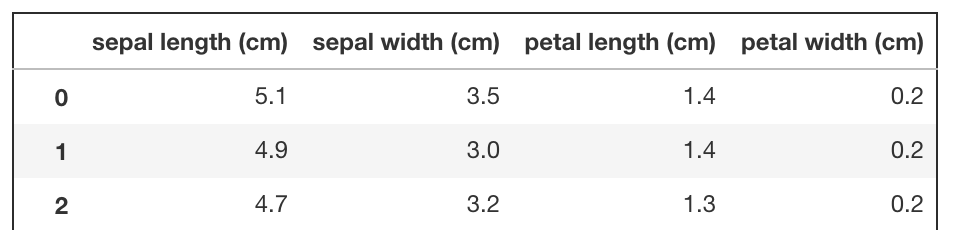
扱いやすいようにデータフレームに変換します。
import pandas as pd
pd.DataFrame(iris.data, columns=iris.feature_names)
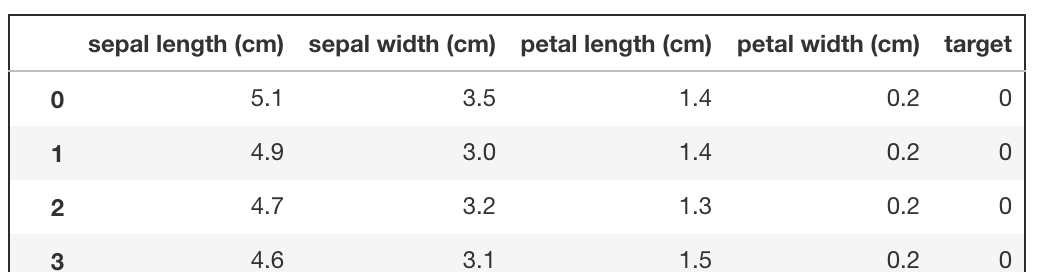
targetも同様にデータフレーム化し、2つの表を結合します。
data = pd.DataFrame(iris.data, columns=iris.feature_names)
target = pd.DataFrame(iris.target, columns=['target'])
pd.concat([data, target], axis=1)
正規性検定
ヒストグラムによる可視化
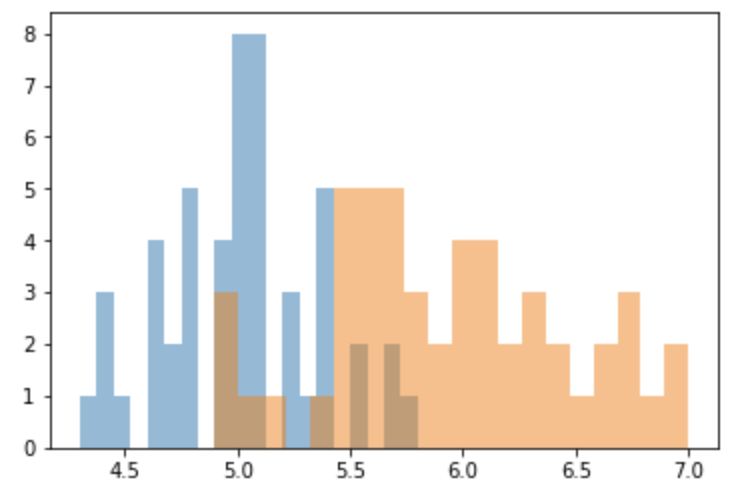
データが正規分布に従うか、ヒストグラムで見てみましょう。
import matplotlib.pyplot as plt
plt.hist(val_setosa, bins=20, alpha=0.5)
plt.hist(val_versicolor, bins=20, alpha=0.5)
plt.show()
ヒストグラムを見る限り、正規分布になっているように思えます。
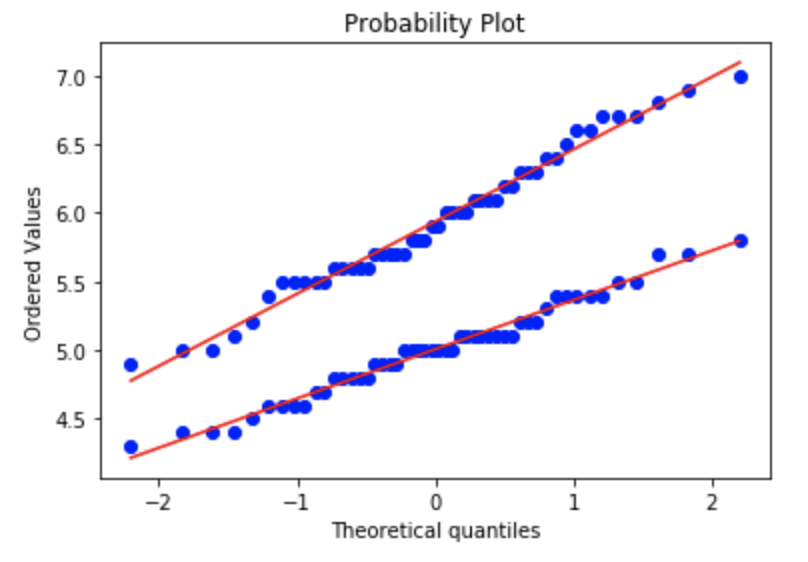
正規Q-Qプロットによる可視化
正規Q-Qプロットは、データが正規分布に従っているかを可視化する方法のひとつです。正規分布に従っていれば、点が直線上に並びます。
from scipy import stats
stats.probplot(val_setosa, dist="norm", plot=plt)
stats.probplot(val_versicolor, dist="norm", plot=plt)
plt.legend(['setosa','', 'versicolor',''])
plt.show()
シャピロ–ウィルク検定
定量的な検定としてはシャピロ–ウィルク検定があります。帰無仮説は「母集団が正規分布である」です。
setosaの場合は下記のようになります。
W, p = stats.shapiro(val_setosa)
print( "p値 = ", p)
# p値 = 0.4595281183719635
versicolorの場合は下記のようになります。
W, p = stats.shapiro(val_versicolor)
print( "p値 = ", p)
# p値 = 0.46473264694213867
両方ともp値が大きいので帰無仮説を棄却できません。
では、データは正規分布に従っているといってもいいのでしょうか。統計的仮説検定では、帰無仮説が棄却されない場合、「帰無仮説は棄却されず、誤っているとは言えない」までしか言うことができません。したがって、帰無仮説が棄却されたからと言って、データが正規分布に従っていると言い切ることができないことに注意してください。ちなみにすべての正規性検定の帰無仮説が「母集団が正規分布である」なので、検定では正規性を結論できません。
今回はヒストグラム、正規Q-Qプロット、シャピロ–ウィルク検定の結果を踏まえて、正規分布であると判断することにします、。
ちなみにデータ数が多い場合はコルモゴロフ-スミルノフ検定を使用します。データ数が数千以上が目安です。3
setosaの場合。
KS, p = stats.kstest(val_setosa, "norm")
print( "p値 = ", p)
# p値 = 0.0
versicolorの場合。
KS, p = stats.kstest(val_versicolor, "norm")
print( "p値 = ", p)
# p値 = 0.0
データ数が50しかないため正常に判定できていないようです。
分散の検定
2標本の母平均の差の検定をするには、2標本の母分散が等しいか、等しくないかで検定手法が異なります。2標本の母分散が等分散かどうかを検定するのがF検定です。帰無仮説は「2標本は等分散である」です。
F検定はScipyに実装されていないので、F統計量を求め、F分布のパーセント点と比較します。今回は両側5%検定とします。
import numpy as np
m = len(val_versicolor)
n = len(val_setosa)
var_versicolor = np.var(val_versicolor) # 0.261104
var_setosa = np.var(val_setosa) # 0.12176400000000002
F = var_versicolor/var_setosa # 2.1443447981340951
# 両側5%検定
F_ = stats.f.ppf(0.975, m-1, n-1) # alpha/2 #1.7621885352431106
if F > F_:
print('「等分散である」を棄却')
else:
print('「等分散である」を受容')
# 「等分散である」を棄却
検定によって帰無仮説が棄却され、有意水準5%で等分散でないことが示されました。
平均の検定
targetの値に応じてデータを抽出し、statsのt検定メソッドを使用します。
data = pd.DataFrame(iris.data, columns=iris.feature_names)
target = pd.DataFrame(iris.target, columns=['target'])
df = pd.concat([data, target], axis=1)
val_setosa = df[df['target']==0].loc[:, 'sepal length (cm)'].values
val_versicolor = df[df['target']==1].loc[:, 'sepal length (cm)'].values
t, p = stats.ttest_ind(val_setosa, val_versicolor, equal_var=False)
print( "p値 = ", p)
# p値 = 3.74674261398e-17
stats.ttest_indは独立な2標本に対する検定で使用します。等分散でない場合はequal_var=Falseとします。別名welchのt検定です。等分散が仮定できる場合はTrueにします。
対応のある2標本のときはstats.ttest_relを使用します。
今回は独立な2標本でかつ、等分散が棄却されたのでstats.ttest_ind、equal_var=False としました。
p値が0.01よりも小さいので、有意水準1%で帰無仮説「母平均が等しい」を棄却します。
ちなみに標本平均は下記のようになります。
print(np.mean(val_setosa))
print(np.mean(val_versicolor))
# 5.006
# 5.936
おわりに
今回は2標本の平均値の検定を行いました。ライブラリを使用することで検定統計量やp値がすぐに計算できるのは便利ですね。
-
『Iris flower data set - Wikipedia』(https://en.wikipedia.org/wiki/Iris_flower_data_set) ↩
-
田中美里,廣安 知之,日和悟『統計検定における考え方と手順』(2015)(http://www.is.doshisha.ac.jp/isreport2/wp-content/uploads/2016/02/20160216-misato.pdf) ↩
-
『4章 母集団と指定値との量的データの検定』(http://www.heisei-u.ac.jp/ba/fukui/pdf/apstattext04.pdf) ↩