More than 1 year has passed since last update.

適応共鳴理論(Adaptive Resonance Theory)の異常検知への適用

Posted at 2021-12-25

はじめに

異常検知を現実的問題に適用する時の問題として、異常クラスの多さと未知の異常の存在があります。とある設備を点検する上で、人間による目視点検ではおかしいと気づける状態を明確に分類、記述しようとすると物凄いたくさんのパターンの異常状態を定義する必要があります。また、設備を運用していく中で、想定していなかった新たな異常が発生する場合もあります。

したがって、異常検知のアルゴリズムとして未知の異常の検出と、検出した未知の異常を一つのクラスとして分類、記憶していくことが必要となります。正常データを基準にして異常を判定するアルゴリズムはたくさんありますが、未知データにラベル付をしていくアルゴリズムは多くありません。

この記事では検出した異常をクラス分類し、ラベルを付けていくアルゴリズムの一つとして適応共鳴理論(Adaptive Resonance Theory)を紹介します。

参考

Leonardo Enzo Brito da Silva, Islam Elnabarawy, Donald C. Wunsch II, "A Survey of Adaptive Resonance Theory Neural Network Models for Engineering Applications", 2019
Mohammad-Taghi, Vakil-Baghmisheh, Nikola Pavešić, "A Fast Simplified Fuzzy ARTMAP Network", 2003
堀嘉成, "適応共鳴理論を利用したプラントの監視・診断方法に関する研究", 2019
他の論文は脚注に記載しました

適応共鳴理論(Adaptive Resonance Theory)の概説

適応共鳴理論(Adaptive Resonance Theory; ART)は、1976年にGrossberg¹は
周囲の環境の変化を、脳がどのように意識的に注意を向け、学習し、パターンを認識するようになるかについて、生物学的妥当性を基にした理論です。この理論では神経回路（ニューラルネットワーク）は共鳴によるフィードバックによって学習が制御されていると考えています。

適応共鳴理論は安定性と可塑性の問題にアプローチしています。可塑性とは、学習アルゴリズムが新しいパターンに適応し、学習する能力のことです。学習系の多くでは、可塑性が不安定性をもたらすことがあります。これは、系が新しい知識を学習することによって、以前に学習した知識が失われたり破損したりする状況であり、破局的忘却とも呼ばれます。一方、安定性とは、クラスタを代表するベクトルであるプロトタイプベクトルが以前の値を取ることができない（非周期的）こと、および入力データが無限にあったときに有限個のクラスタが形成されることを指します。

適応共鳴理論は、この安定性と可塑性のジレンマを解決するために、破局的な忘却を起こすことなく、任意の入力パターンを高速かつ安定的に自己組織的に学習するアルゴリズムとして考案されました。

1987年、CarpenterとGrossbergは、二値ベクトルを入力とする自己組織化クラスタリングの手法として、ART1と呼ばれるアルゴリズムを発表しました²。しかし、その数学的な難解さと、二値ベクトルの自己組織化クラスタリングにしか使えないことから、あまり注目されることはありませんでした。

その後、1987年から1992年にかけて連続値を成分に持つベクトルを入力可能にしたART2と呼ばれるアルゴリズム³、連続値とバイナリの任意の入力パターン列に対して対応可能なFuzzy ARTと呼ばれるアルゴリズム⁴、教師ありに拡張されたARTMAPと呼ばれるアルゴリズム⁵などが考案されました。他にもsimplified fuzzy ARTMAP (SFAM)⁶といった修正モデルや簡略化モデルがいくつも考案されており、数学的複雑性が取り除かれること（共鳴構造の排除）によって利用する人も増えてきました。

適応共鳴理論(Adaptive Resonance Theory)のアルゴリズム

以下では、現代的で簡略的な形式の適応共鳴理論のアルゴリズムを解説します。

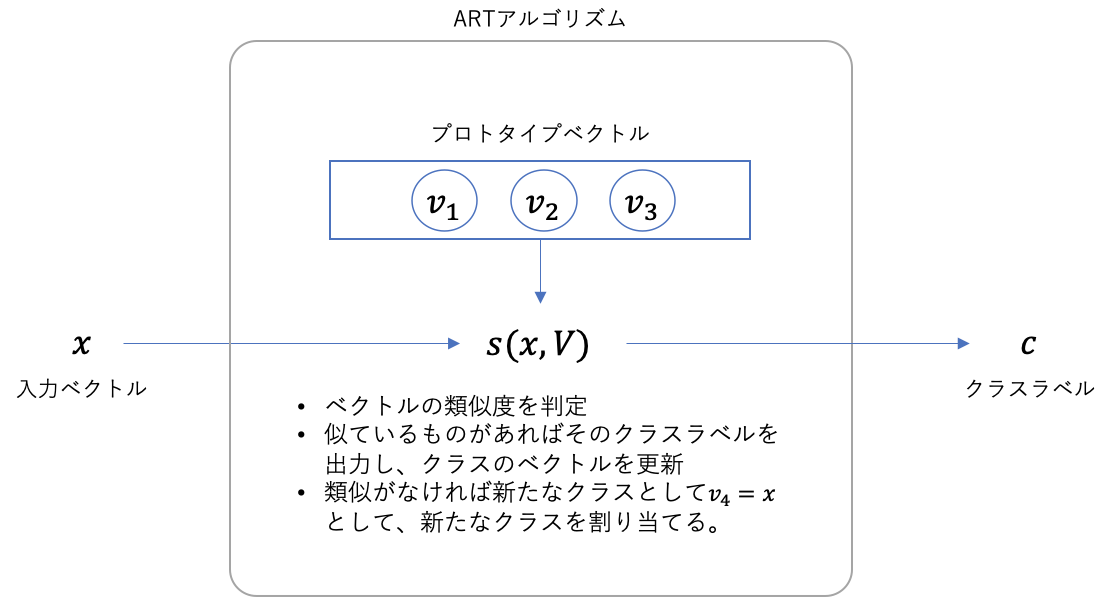
適応共鳴理論が行うタスクはクラスタリングです。入力データ$D$は$N$個の$m$次元の実数値ベクトル$\boldsymbol{x}^{(1)},...,\boldsymbol{x}^{(N)}$であるとします。バイナリベクトルでも適用できるように以下では抽象的に解説します。

まず、1つ目のデータが入力されたらこれを$\boldsymbol{v}_1=\boldsymbol{x}^{(1)}$として保存し、$\boldsymbol{x}^{(1)}$をクラス1に割り当てます。
次に2つ目のデータ$\boldsymbol{x}^{(2)}$が入力されたら保存されているベクトルとの類似度$s(\boldsymbol{x}^{(2)}, \boldsymbol{v}_1)$を計算します。類似度$s(\boldsymbol{x}, \boldsymbol{y})$はベクトルが連続値をとるならコサイン類似度等、バイナリならJaccard 係数等が使用可能で、予め使用するものを決めておきます。類似度$s$の値が、予め決めておいた閾値$t$を超えていたら$\boldsymbol{x}^{(2)}$をクラス1に割り当てます。そしてプロトタイプベクトル$\boldsymbol{v}_1$を$\boldsymbol{x}^{(2)}$を用いて更新します。閾値を下回っていた場合は、$\boldsymbol{x}^{(2)}$をクラス2に割り当て、$\boldsymbol{v}_2=\boldsymbol{x}^{(2)}$として保存します。ここでは保存されたとして話を進めましょう。
次に3つ目のデータ$\boldsymbol{x}^{(3)}$が入力されたらストアされているベクトルとの類似度$s(\boldsymbol{x}^{(3)}, \boldsymbol{v}_1)$、$s(\boldsymbol{x}^{(3)}, \boldsymbol{v}_2)$を計算します。$\boldsymbol{x}^{(3)}$を類似度$s$の値が一番大きくかつ、閾値$t$を超えているクラスに割り当て、プロトタイプベクトルを更新します。閾値を下回った場合は$\boldsymbol{x}^{(3)}$をクラス3に割り当て、$\boldsymbol{v}_3=\boldsymbol{x}^{(3)}$として保存します。
以上と同じ操作を$\boldsymbol{x}^{(N)}$まで繰り返します。

これでクラスタリングの学習が完了です。アルゴリズムのハイパーパラメータは類似度と閾値です。また、このアルゴリズムによるクラスタリング結果はデータを入力する順番に依存しますので、この影響をなるべく抑えるために、$\boldsymbol{x}^{(1)},...,\boldsymbol{x}^{(N)}$を何回も繰り返して入力することもできます。

学習済みモデルを使用した推論では、上と同様に推論対象データ$\boldsymbol{x}^{(N+1)}$の類似度$s$の値が一番大きくかつ、閾値$t$を超えているクラスに割り当てるか、閾値を下回った場合は未知クラスとして出力します。したがってこのモデルは未知クラスの検出に使用できます。

アルゴリズムの注意点

クラスタリング結果がデータの順番に依存する。
クラスタリング結果が閾値の設定に敏感なため、閾値設定が難しい。

実装例

ここではartlearnというライブラリを使用します。

pip install artlearn

L2距離を用いた適応共鳴理論

一番わかり易い例としてL2距離を用いた適応共鳴理論を紹介します。このモデルではベクトル間のL2距離が閾値を下回ったら同じクラスとして割り当てます。

まずデータを準備します。

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import MinMaxScaler

from artlearn import L2ART

sns.set()


def prepare_data():
    X, y = make_blobs(n_samples=300, centers=6, n_features=2, cluster_std=0.6, random_state=0)
    scaler = MinMaxScaler()
    X = scaler.fit_transform(X)
    return X, y

# prepare data
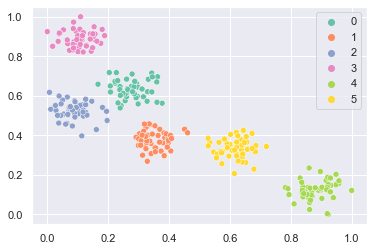
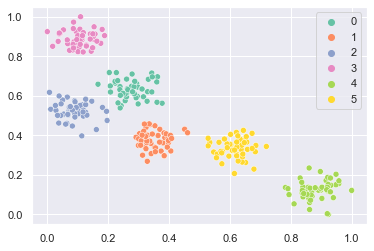
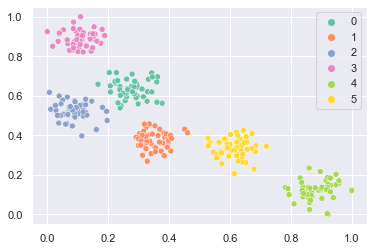
X, y = prepare_data()
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, palette="Set2")
plt.show()

学習を行います。このライブラリでは$\boldsymbol{x}^{(1)},...,\boldsymbol{x}^{(N)}$を何回も繰り返してイテレーションを行っているので、max_iterを指定する必要があります。また、閾値設定が厳しい場合、クラスが大量にできるため計算量が増えて実行時間が大きくなる可能性があるので、max_classで最大クラス数を設定します。rhoは閾値です。betaは学習率で、プロトタイプベクトルが$\boldsymbol{v} \leftarrow \beta \boldsymbol{x} + (1-\beta)\boldsymbol{v}$と更新されます。

# learning
clf = L2ART(max_iter=100, max_class=100, rho=0.2, beta=0.1)
clf.fit(X)

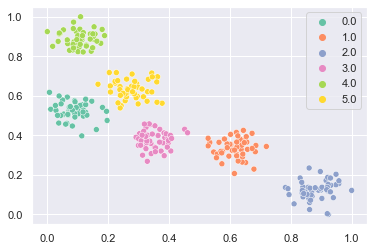
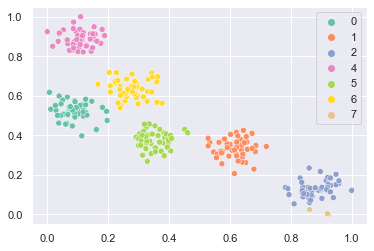
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=clf.labels_, palette="Set2")
plt.show()

例えばクラスタ結果から遠い点に対して推論すると未知クラスとして出力されます。

clf.predict([[0.6, 0.9]])  # array([-1], dtype=int32)

Bayesian ART

データの分布が多峰の多次元ガウス分布に従っていると考えたBayesian ARTを紹介します。

まずデータを準備します。

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import MinMaxScaler

from artlearn import BayesianART

sns.set()


def prepare_data():
    X, y = make_blobs(n_samples=300, centers=6, n_features=2, cluster_std=0.6, random_state=0)
    scaler = MinMaxScaler()
    X = scaler.fit_transform(X)
    return X, y


# prepare data
X, y = prepare_data()
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, palette="Set2")
plt.show()

学習を行います。Bayesian ARTでは類似度として尤度を使用しています。したがってrhoは尤度の閾値です。sigmaは事前分布の標準偏差です。max_hyper_volumeはもう一つの閾値パラメータで、ガウス分布の分散共分散行列をもとに計算したハイパーボリュームの最大値を指定します。

# learning
clf = BayesianART(max_iter=3, max_class=100, rho=0.01, sigma=0.05, max_hyper_volume=0.07)
clf.fit(X)

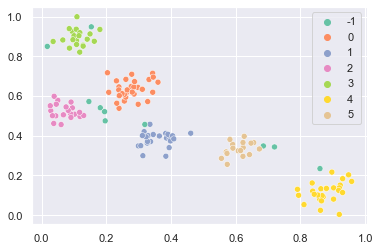
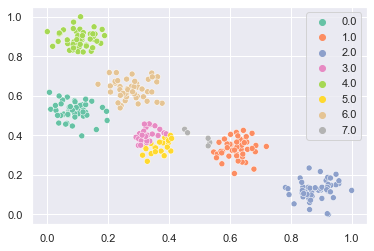
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=clf.labels_, palette="Set2")
plt.show()

クラス7に分類される点が生じてしまっていますね。適応共鳴理論の制御の難しいところです。

SFAM

教師ありの適応共鳴理論であるSFAMを紹介します。SFAMでは適応共鳴理論のアルゴリズムでクラスタリングを行い、得られたクラスタ結果$y^{(1)},...,y^{(N)}$を教師のラベル$z^{(1)},...,z^{(N)}$にマップする写像を作成することによって教師あり学習として実行します。

300点のデータを作成し、150点を学習に、150点を予測に使用します。

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import MinMaxScaler

from artlearn import SFAM

sns.set()


def prepare_data():
    X, y = make_blobs(n_samples=300, centers=6, n_features=2, cluster_std=0.6, random_state=0)
    scaler = MinMaxScaler()
    X = scaler.fit_transform(X)
    X_ = X.copy()
    X_ = np.hstack([X, 1.0 - X_])
    return X_, y


# prepare data
X, y = prepare_data()
sns.scatterplot(x=X[:150, 0], y=X[:150, 1], hue=y[:150], palette="Set2")
plt.show()

予測するデータは次のようになります。

# prepare data
X, y = prepare_data()
sns.scatterplot(x=X[150:, 0], y=X[150:, 1], hue=y[150:], palette="Set2")
plt.show()

学習を行います。rhoは閾値です。betaは学習率です。

# learning
clf = SFAM(max_iter=100, max_class=100, rho=0.9, beta=0.1)
clf.fit(X[:150], y[:150])
y_pred = clf.predict(X[150:])

print("score:", clf.score(X[150:], y[150:]))
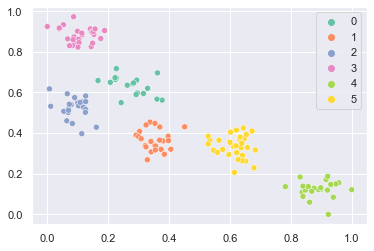
sns.scatterplot(x=X[150:, 0], y=X[150:, 1], hue=y_pred, palette="Set2")
plt.show()

クラスタの端の方にある点は未知クラスとして分類されています。

ART2A

こちらはART2の修正版アルゴリズムです。

まずデータを準備します。

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import MinMaxScaler

from artlearn import ART2A

sns.set()

def prepare_data():
    X, y = make_blobs(n_samples=300, centers=6, n_features=2, cluster_std=0.6, random_state=0)
    scaler = MinMaxScaler()
    X = scaler.fit_transform(X)
    X_ = X.copy()
    X_ = np.hstack([X, 1.0 - X_])
    return X_, y


# prepare data
X, y = prepare_data()
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, palette="Set2")
plt.show()

学習を行います。したがってrho_starは閾値です。etaは学習率です。thetaはデータにノイズが含まれている場合の閾値で、この閾値を下回る信号のデータはノイズとして除去されます。

# learning
clf = ART2A(max_iter=100, max_class=100, theta=0.0, eta=0.01, rho_star=0.95)
clf.fit(X)

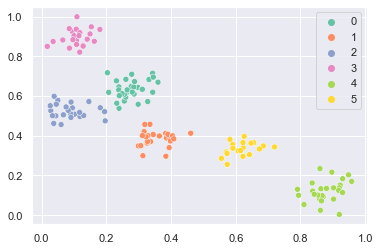
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=clf.labels_, palette="Set2")
plt.show()

ART2Aではベクトルは1に正規化され内積で類似度を計算するため、角度によってクラスタリングされます。

おわりに

この記事では適応共鳴理論(Adaptive Resonance Theory)を紹介しました。適応共鳴理論はクラスタリング結果がハイパーパラメータに対して敏感なので、取り扱いが難しいアルゴリズムですが、非常にシンプルなアルゴリズムなので自分で改良を加えていくことができます。系の特性に合わせてオリジナルのARTを作れば十分実用的な自作アルゴリズムを作ることができると思います。

Grossberg, S. ,"Adaptive pattern classification and universal recoding: II Feedback, expectation, olfaction, illusions", 1976 ↩
Gail A.Carpenter, Stephen Grossberg, "A massively parallel architecture for a self-organizing neural pattern recognition machine", 1987 ↩
Gail A. Carpenter and Stephen Grossberg, "ART 2: self-organization of stable category recognition codes for analog input patterns", 1987 ↩
Gail A.Carpenter, Stephen Grossberg, David B.Rosen, "Fuzzy ART: Fast stable learning and categorization of analog patterns by an adaptive resonance system", 1991 ↩
Gail A.Carpenter, Stephen Grossberg, John H.Reynolds, "ARTMAP: Supervised real-time learning and classification of nonstationary data by a self-organizing neural network", 1991 ↩
Mohammad-Taghi, Vakil-Baghmisheh, Nikola Pavešić, "A Fast Simplified Fuzzy ARTMAP Network", 2003 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up