はじめに
データを取得したセンサの仕様などによって、本当は連続値であるものを離散値で計測する場合があります。例えば、センサのクロック周波数の仕様や、ストレージの容量節約のために測定を2秒おきにすると、測定値が連続に変化せず、離散的に変化する結果となります。2秒より小さい刻み幅で、例えば1秒の単位でデータを加工したい場合、なんらかの手法で不足しているデータの補間をする必要があります。
今回はScipyのinterpolate.interp1dを使用して補完をしてみます。
参考
- Scipy.org,『scipy.interpolate.interp1d』,https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.interp1d.html
- 山本昌志,『スプライン補間』,平成18年11月27日,http://www.yamamo10.jp/yamamoto/lecture/2006/5E/interpolation/interpolation_html/node3.html
手順
次の関数
y = x \ \mathrm{sin}x,
から$x = 1,2,...,10$のときの$y$の値をサンプリングします。これらの点の間の補完を通して、保管の手法を見ていきます。
import matplotlib.pyplot as plt
import numpy as np
def g(x):
return x*np.sin(2*x)
x = np.linspace(0, 10, num=11)
y = g(x)
plt.plot(x, y, 'o')
plt.grid(True)
# 比較のためのグラフ
u = np.linspace(0, 10, num=101)
v = g(u)
plt.plot(u, v, alpha=0.2)
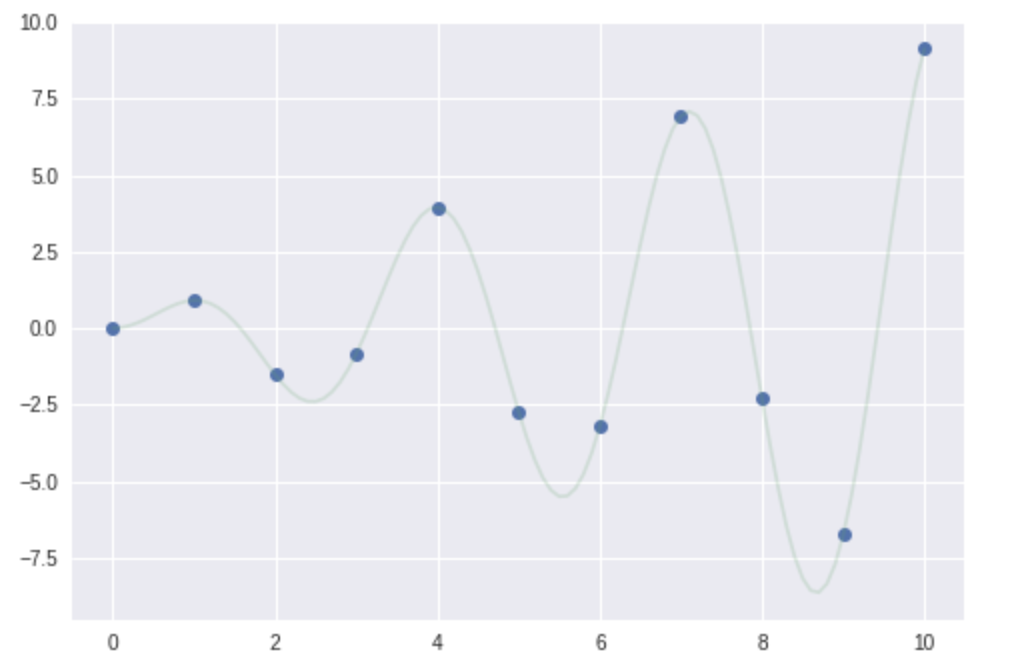
線形補完
線形補間は2点のデータを直線(すなわち線形)で結び補完する方法です。データの間隔が小さければ良い近似になりますが、間隔が大きい場合は誤差が大きくなります。
from scipy import interpolate
f = interpolate.interp1d(x, y, kind='linear')
plt.plot(u, f(u),'-')
plt.grid(True)
# 比較のためのグラフ
plt.plot(u, g(u), alpha=0.2)

スプライン補間
スプライン補間は、データを短区間に区切って低次の多項式で補完したものです。下記は3次の補完をしました。
f2 = interpolate.interp1d(x, y, kind='cubic')
plt.plot(u, f2(u), '-')
plt.grid(True)
# 比較のためのグラフ
plt.plot(u, g(u), alpha=0.2)

その他
kindで補完する方法を選べます。
| 補完の手法 | kind |
|---|---|
| 線形補間 | 'linear' |
| スプライン補間 | 'zero', 'slinear', 'quadratic', 'cubic' |
| 直前の点の値 | 'previous' |
| 直後の点の値 | 'next' |
| 一番近い点の値 | 'nearest' |
f3 = interpolate.interp1d(x, y, kind='nearest')
plt.plot(u, f3(u), '-')
plt.grid(True)
# 比較のためのグラフ
plt.plot(u, g(u), alpha=0.2)

データの外側の補完
fill_value='extrapolate'とするとデータの外を補完できますが、もちろん離れれば離れるほど当てはまりは悪くなります。'cubic'の補完では11すら当てはまりません。
f4 = interpolate.interp1d(x, y, 'cubic', fill_value='extrapolate')
z = np.linspace(0, 12, num=121)
plt.plot(z, f4(z), '-')
plt.grid(True)
# 比較のためのグラフ
plt.plot(z, g(z), alpha=0.2)

おわりに
データの補完をやってみました。点と点の間で関数が激しく振動しなければ、データ間の補完はそれなりに合っていそうです。しかし、データの範囲外にもこの手法を用いるとただちに破綻します。データの範囲外で外装したい場合は、きちんと予測モデルを構築する必要があります。