はじめに
PythonのライブラリStatsModelsを使用して重回帰分析をやってみます。Rと違って少々不便です。
環境
- Google Colaboratory
- statsmodels==0.9.0
参考
手順
データの読み込み
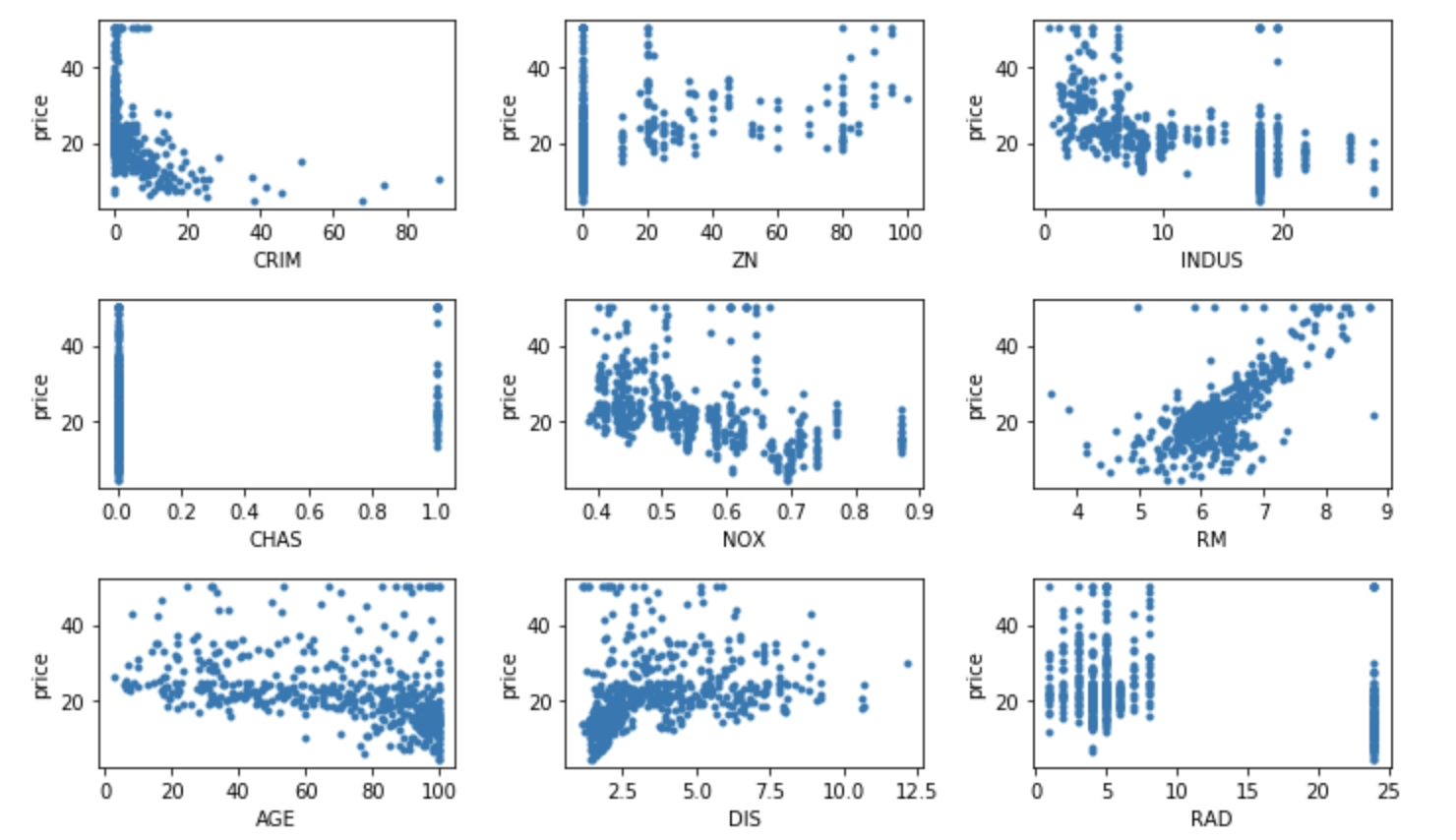
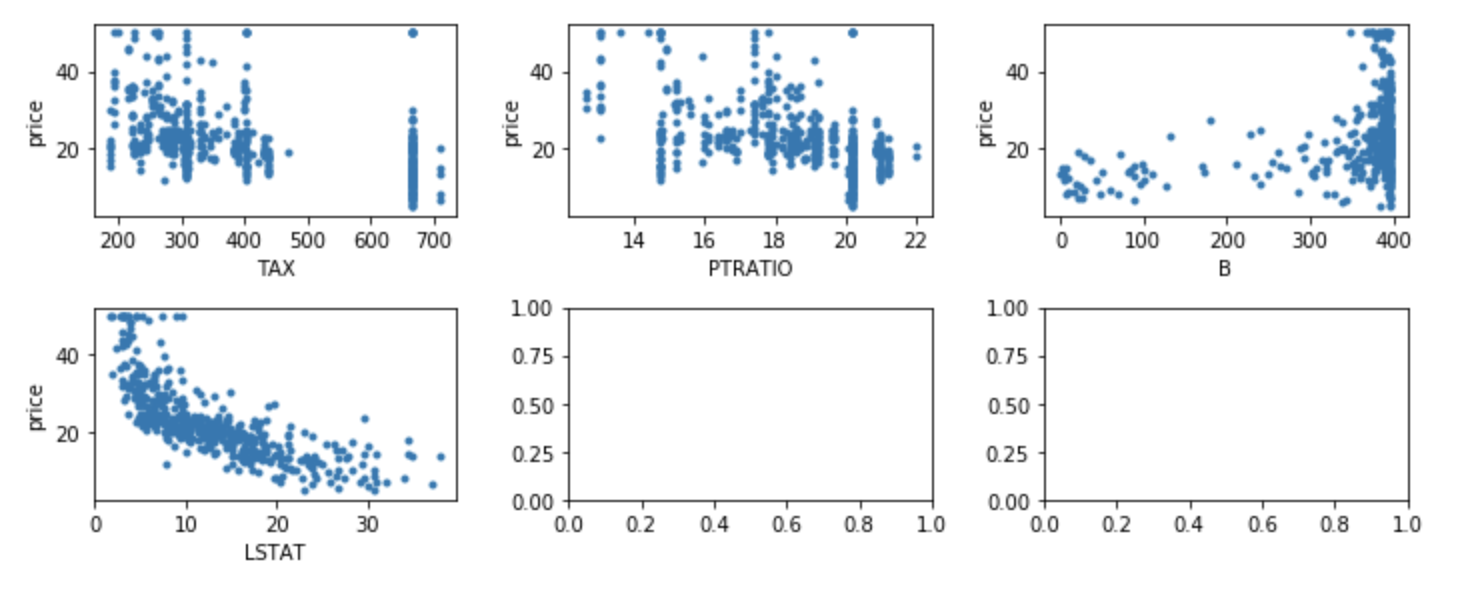
ボストン市の住宅価格データを使用します。ボストン市の住宅価格を目的変数、NOxの濃度や部屋数などを説明変数として持っているデータです。
scipyが1.3だとstatsmodelsの0.9.0が使用できないのでダウングレード後、ランタイムを再起動します。
!pip install scipy==1.2
データを読み込み、プロットして確認してみます。
# 必須のモジュール
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_boston
# データを読み込み
boston = load_boston()
# 目的変数と説明変数の関係を確認
fig, ax = plt.subplots(5, 3, figsize=(15, 15))
xlabels = boston.feature_names
for i in range(5):
for j in range(3):
if 3*i+j >= 13:
break
ax[i, j].scatter(boston.data[:, 3*i+j], boston.target, marker='.')
ax[i, j].set_xlabel(xlabels[3*i+j])
ax[i, j].set_ylabel("price")
plt.tight_layout()
plt.show()
相関係数を算出
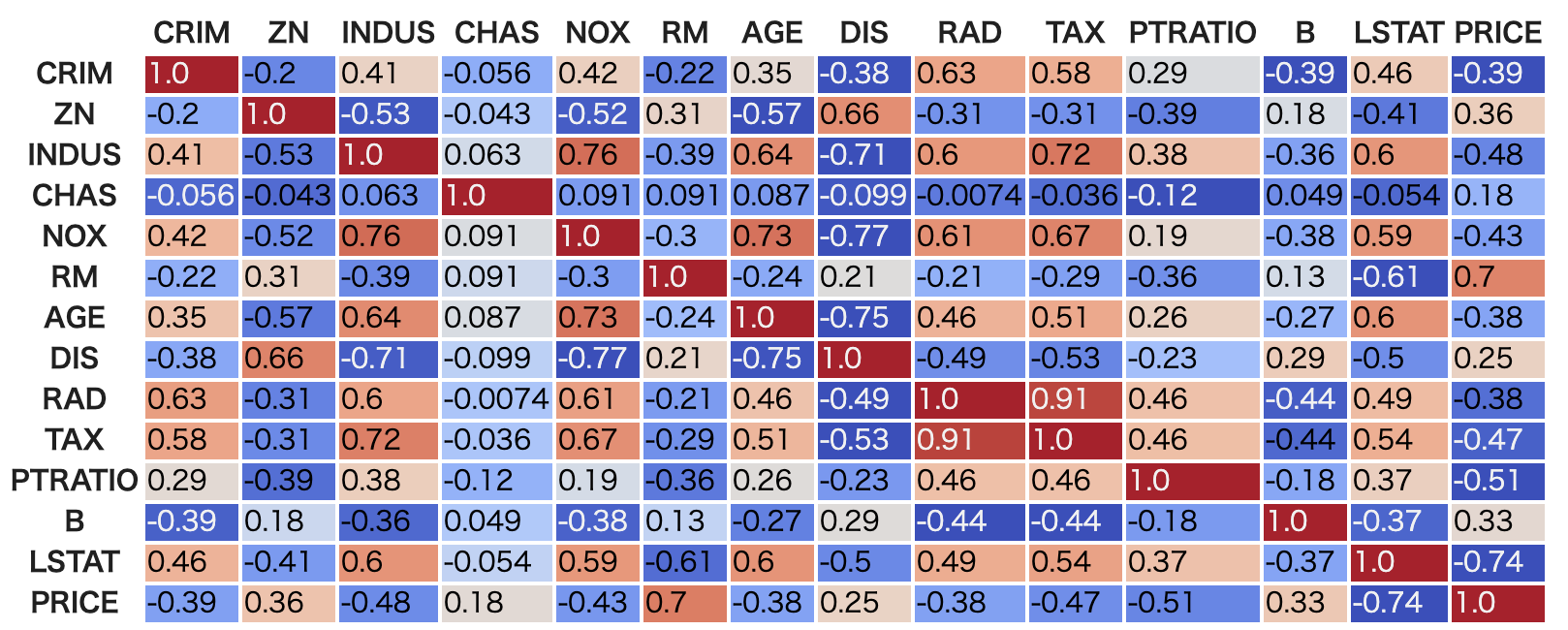
重回帰分析をする上では変数間の相関が、多重共線性として問題になります。そこで変数間の相関を確認しておきます。
# 目的変数と説明変数を一つのデータフレームにまとめる
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target
# 相関を計算
corr = df.corr()
# データフレームに色をつける
corr.style.format("{:.2}").background_gradient(cmap=plt.get_cmap('coolwarm'), axis=1)
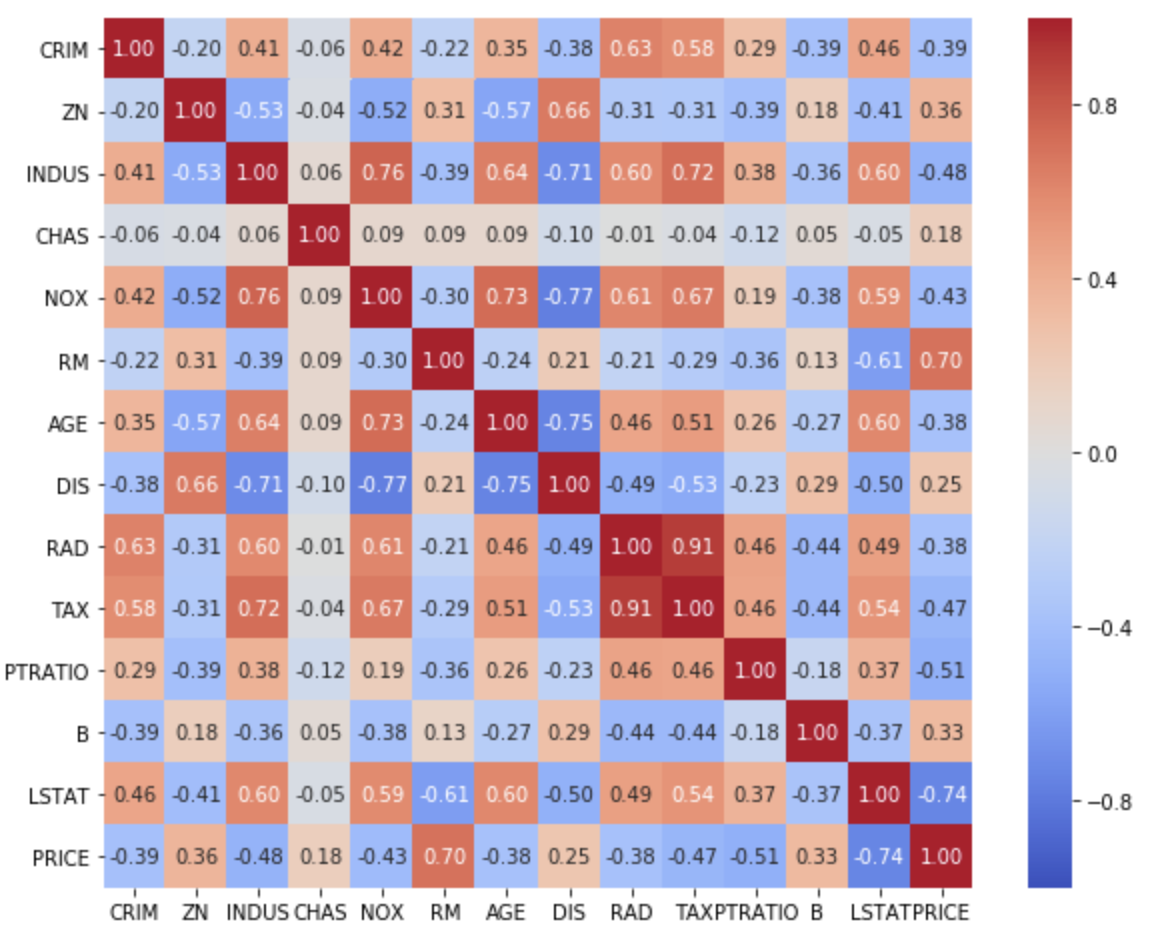
seabornでも同様のヒートマップを作成できます。
fig, ax = plt.subplots(figsize=(10, 8))
sns.heatmap(corr, vmax=1, vmin=-1, center=0, annot=True, cbar=True, cmap='coolwarm', square=True, fmt='.2f', ax=ax)
変数減少法で重回帰分析
変数減少法を使用して分析してみます。
まずデータを準備します。
from sklearn.model_selection import train_test_split
X = df.drop('PRICE', axis=1)
y = df['PRICE']
# テータ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size =0.8, random_state=0)
全変数を使用して重回帰分析をしてみます。
import statsmodels.api as sm
# 回帰モデル作成
mod = sm.OLS(y_train, sm.add_constant(X_train))
# 訓練
result = mod.fit()
# 統計サマリを表示
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: PRICE R-squared: 0.773
Model: OLS Adj. R-squared: 0.765
Method: Least Squares F-statistic: 102.2
Date: Thu, 23 May 2019 Prob (F-statistic): 9.64e-117
Time: 17:39:57 Log-Likelihood: -1171.5
No. Observations: 404 AIC: 2371.
Df Residuals: 390 BIC: 2427.
Df Model: 13
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 38.0917 5.522 6.898 0.000 27.234 48.949
CRIM -0.1194 0.037 -3.257 0.001 -0.192 -0.047
ZN 0.0448 0.014 3.102 0.002 0.016 0.073
INDUS 0.0055 0.063 0.087 0.931 -0.119 0.130
CHAS 2.3408 0.902 2.595 0.010 0.567 4.115
NOX -16.1236 4.212 -3.828 0.000 -24.404 -7.843
RM 3.7087 0.458 8.106 0.000 2.809 4.608
AGE -0.0031 0.014 -0.218 0.828 -0.031 0.025
DIS -1.3864 0.214 -6.480 0.000 -1.807 -0.966
RAD 0.2442 0.070 3.481 0.001 0.106 0.382
TAX -0.0110 0.004 -2.819 0.005 -0.019 -0.003
PTRATIO -1.0459 0.137 -7.636 0.000 -1.315 -0.777
B 0.0081 0.003 2.749 0.006 0.002 0.014
LSTAT -0.4928 0.054 -9.086 0.000 -0.599 -0.386
==============================================================================
Omnibus: 141.494 Durbin-Watson: 1.996
Prob(Omnibus): 0.000 Jarque-Bera (JB): 629.882
Skew: 1.470 Prob(JB): 1.67e-137
Kurtosis: 8.365 Cond. No. 1.55e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.55e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
多重共線性の疑いのある変数を探します。
最初にそれぞれの説明変数と目的変数の相関係数を計算しました。もし変数が独立であれば、回帰係数も相関係数と同じ符号になるはずです。しかし多重共線性があると、回帰係数が一意に決まらず不安定になり、相関係数と異なる符号になる場合があります。これを確認してみます。
# constを除くために1から始める
np.sign(result.params[1:])
# 目的変数を除くために-1までとする
np.sign(corr['PRICE'][:-1])
# 0でない変数が相関している可能性あり
np.sign(result.params[1:]) - np.sign(corr['PRICE'][:-1])
CRIM 0.0
ZN 0.0
INDUS 2.0
CHAS 0.0
NOX 0.0
RM 0.0
AGE 0.0
DIS -2.0
RAD 2.0
TAX 0.0
PTRATIO 0.0
B 0.0
LSTAT 0.0
dtype: float64
INDUS、DIS、RADを取り除いて回帰分析してみます。
# 回帰モデル作成
d = ['INDUS', 'DIS', 'RAD']
mod = sm.OLS(y_train, sm.add_constant(X_train.drop(d, axis=1)))
# 訓練
result = mod.fit()
# 統計サマリを表示
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: PRICE R-squared: 0.742
Model: OLS Adj. R-squared: 0.735
Method: Least Squares F-statistic: 112.9
Date: Thu, 23 May 2019 Prob (F-statistic): 5.42e-109
Time: 17:42:50 Log-Likelihood: -1197.5
No. Observations: 404 AIC: 2417.
Df Residuals: 393 BIC: 2461.
Df Model: 10
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 19.6164 5.196 3.776 0.000 9.402 29.831
CRIM -0.0603 0.037 -1.632 0.104 -0.133 0.012
ZN 0.0022 0.014 0.158 0.874 -0.025 0.029
CHAS 2.9510 0.949 3.111 0.002 1.086 4.816
NOX -5.3578 4.024 -1.331 0.184 -13.269 2.554
RM 4.4060 0.471 9.359 0.000 3.480 5.332
AGE 0.0202 0.015 1.393 0.164 -0.008 0.049
TAX -0.0003 0.002 -0.122 0.903 -0.005 0.004
PTRATIO -1.0610 0.141 -7.516 0.000 -1.339 -0.783
B 0.0076 0.003 2.457 0.014 0.002 0.014
LSTAT -0.4918 0.057 -8.562 0.000 -0.605 -0.379
==============================================================================
Omnibus: 166.959 Durbin-Watson: 1.995
Prob(Omnibus): 0.000 Jarque-Bera (JB): 885.215
Skew: 1.706 Prob(JB): 6.00e-193
Kurtosis: 9.399 Cond. No. 1.35e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.35e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
もう一度確認。
(np.sign(result.params[1:]) - np.sign(corr['PRICE'][:-1])).dropna()
AGE 2.0
B 0.0
CHAS 0.0
CRIM 0.0
LSTAT 0.0
NOX 0.0
PTRATIO 0.0
RM 0.0
TAX 0.0
ZN 0.0
dtype: float64
今度はAGEを落としてみる。
OLS Regression Results
==============================================================================
Dep. Variable: PRICE R-squared: 0.741
Model: OLS Adj. R-squared: 0.735
Method: Least Squares F-statistic: 125.0
Date: Thu, 23 May 2019 Prob (F-statistic): 1.23e-109
Time: 17:47:01 Log-Likelihood: -1198.5
No. Observations: 404 AIC: 2417.
Df Residuals: 394 BIC: 2457.
Df Model: 9
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 18.1151 5.089 3.560 0.000 8.111 28.120
CRIM -0.0622 0.037 -1.682 0.093 -0.135 0.011
ZN -0.0037 0.013 -0.284 0.777 -0.030 0.022
CHAS 2.9959 0.949 3.156 0.002 1.130 4.862
NOX -2.8646 3.609 -0.794 0.428 -9.959 4.230
RM 4.5634 0.458 9.973 0.000 3.664 5.463
TAX -0.0004 0.002 -0.165 0.869 -0.005 0.004
PTRATIO -1.0582 0.141 -7.488 0.000 -1.336 -0.780
B 0.0082 0.003 2.656 0.008 0.002 0.014
LSTAT -0.4617 0.053 -8.664 0.000 -0.566 -0.357
==============================================================================
Omnibus: 176.632 Durbin-Watson: 1.980
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1038.791
Skew: 1.782 Prob(JB): 2.69e-226
Kurtosis: 10.001 Cond. No. 1.27e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.27e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
(np.sign(result.params[1:]) - np.sign(corr['PRICE'][:-1])).dropna()
B 0.0
CHAS 0.0
CRIM 0.0
LSTAT 0.0
NOX 0.0
PTRATIO 0.0
RM 0.0
TAX 0.0
ZN -2.0
dtype: float64
今度はZNを落としてみる。
OLS Regression Results
==============================================================================
Dep. Variable: PRICE R-squared: 0.741
Model: OLS Adj. R-squared: 0.735
Method: Least Squares F-statistic: 140.9
Date: Thu, 23 May 2019 Prob (F-statistic): 1.04e-110
Time: 17:48:32 Log-Likelihood: -1198.5
No. Observations: 404 AIC: 2415.
Df Residuals: 395 BIC: 2451.
Df Model: 8
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 17.6474 4.809 3.670 0.000 8.193 27.102
CRIM -0.0625 0.037 -1.695 0.091 -0.135 0.010
CHAS 3.0095 0.947 3.178 0.002 1.148 4.871
NOX -2.3888 3.192 -0.748 0.455 -8.664 3.887
RM 4.5523 0.455 9.997 0.000 3.657 5.448
TAX -0.0005 0.002 -0.232 0.817 -0.005 0.004
PTRATIO -1.0433 0.131 -7.961 0.000 -1.301 -0.786
B 0.0082 0.003 2.666 0.008 0.002 0.014
LSTAT -0.4611 0.053 -8.670 0.000 -0.566 -0.357
==============================================================================
Omnibus: 176.890 Durbin-Watson: 1.980
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1043.397
Skew: 1.784 Prob(JB): 2.69e-227
Kurtosis: 10.018 Cond. No. 1.17e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.17e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
(np.sign(result.params[1:]) - np.sign(corr['PRICE'][:-1])).dropna()
B 0.0
CHAS 0.0
CRIM 0.0
LSTAT 0.0
NOX 0.0
PTRATIO 0.0
RM 0.0
TAX 0.0
dtype: float64
$t^2<2$の変数があるので更に変数を落とす。絶対値が一番小さいTAXを落とす。
OLS Regression Results
==============================================================================
Dep. Variable: PRICE R-squared: 0.740
Model: OLS Adj. R-squared: 0.736
Method: Least Squares F-statistic: 161.4
Date: Thu, 23 May 2019 Prob (F-statistic): 8.14e-112
Time: 17:50:47 Log-Likelihood: -1198.5
No. Observations: 404 AIC: 2413.
Df Residuals: 396 BIC: 2445.
Df Model: 7
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 17.8533 4.721 3.782 0.000 8.572 27.134
CRIM -0.0654 0.035 -1.888 0.060 -0.134 0.003
CHAS 3.0146 0.945 3.188 0.002 1.156 4.873
NOX -2.7882 2.684 -1.039 0.300 -8.065 2.489
RM 4.5483 0.454 10.007 0.000 3.655 5.442
PTRATIO -1.0551 0.121 -8.736 0.000 -1.292 -0.818
B 0.0084 0.003 2.756 0.006 0.002 0.014
LSTAT -0.4611 0.053 -8.680 0.000 -0.566 -0.357
==============================================================================
Omnibus: 175.198 Durbin-Watson: 1.981
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1019.678
Skew: 1.768 Prob(JB): 3.80e-222
Kurtosis: 9.933 Cond. No. 7.56e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 7.56e+03. This might indicate that there are
(np.sign(result.params[1:]) - np.sign(corr['PRICE'][:-1])).dropna()
B 0.0
CHAS 0.0
CRIM 0.0
LSTAT 0.0
NOX 0.0
PTRATIO 0.0
RM 0.0
dtype: float64
今度はNOXを落とす。
# 回帰モデル作成
d = ['INDUS', 'DIS', 'RAD', 'AGE', 'ZN', 'TAX', 'NOX']
mod = sm.OLS(y_train, sm.add_constant(X_train.drop(d, axis=1)))
# 訓練
result = mod.fit()
# 統計サマリを表示
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: PRICE R-squared: 0.740
Model: OLS Adj. R-squared: 0.736
Method: Least Squares F-statistic: 188.1
Date: Thu, 23 May 2019 Prob (F-statistic): 9.72e-113
Time: 17:53:56 Log-Likelihood: -1199.1
No. Observations: 404 AIC: 2412.
Df Residuals: 397 BIC: 2440.
Df Model: 6
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 16.4182 4.515 3.637 0.000 7.543 25.294
CRIM -0.0726 0.034 -2.138 0.033 -0.139 -0.006
CHAS 2.9178 0.941 3.101 0.002 1.068 4.768
RM 4.5315 0.454 9.976 0.000 3.638 5.425
PTRATIO -1.0490 0.121 -8.695 0.000 -1.286 -0.812
B 0.0089 0.003 2.970 0.003 0.003 0.015
LSTAT -0.4830 0.049 -9.903 0.000 -0.579 -0.387
==============================================================================
Omnibus: 168.794 Durbin-Watson: 1.973
Prob(Omnibus): 0.000 Jarque-Bera (JB): 933.196
Skew: 1.711 Prob(JB): 2.29e-203
Kurtosis: 9.613 Cond. No. 7.10e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 7.1e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
(np.sign(result.params[1:]) - np.sign(corr['PRICE'][:-1])).dropna()
B 0.0
CHAS 0.0
CRIM 0.0
LSTAT 0.0
PTRATIO 0.0
RM 0.0
dtype: float64
$t^2<2$の変数はないので、これで終了。決定係数は0.740、自由度調整済み決定係数は0.736となりました。
参考指標としてテストデータの決定係数を計算。
y_pred = result.predict(sm.add_constant(X_test.drop(d, axis=1)))
se = np.sum(np.square(y_test-y_pred))
st = np.sum(np.square(y_test-np.mean(y_test)))
R2 = 1-se/st
print('決定係数:', R2)
決定係数: 0.5009870040610696
おわりに
今回は変数減少法で、各説明変数の有意性に基づいてモデルを作成しました。
他にも変数を増加させる方法や、増減を組み合わせた方法などがあります。Rだとこれらの作業を自動でやってくれるようですがpythonには無いようです。
また、予測性能だけでモデルの良し悪しを測るのであれば、説明変数選択規準を用いてモデルを決めても良いでしょう。この場合は上でやって来たように変数選択をしつつ、選択規準を満たすようなモデルを選ぶことになります。