論文：Prototypical Networks for Few-shot Learning

Info

• タイトル：Prototypical Networks for Few-shot Learning
• カンファ：NeurIPS2017
• 著者：Jake Snell, Kevin Swersky, Richard S. Zemel
• 論文：https://arxiv.org/abs/1703.05175

概要

• 元の訓練データに含まれていなかった、少数しかデータがない新規クラスの分類器を作成するタスクを考える。
• Prototypical Networks を提案。各クラスのプロトタイプ表現への距離を計算することで分類を行うことができる計量空間を学習する。
• プロトタイプのネットワークをゼロショット学習に拡張し、CU-BirdsデータセットにおいてSOTAの結果を得ることができた。

背景

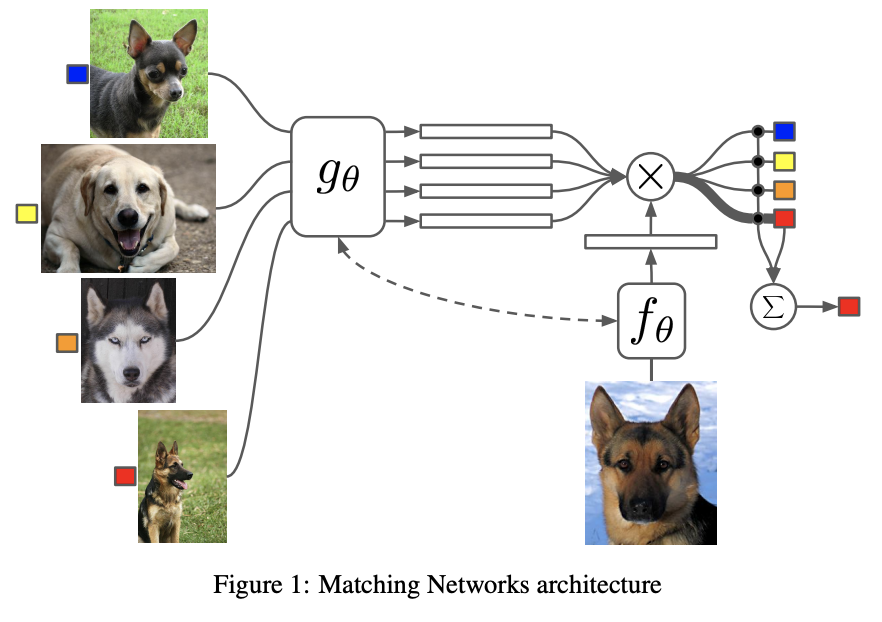
• 最近Few-shot learningでは、2つの手法で進展があった。一つはMatching Networksで、分類したい画像（クエリ画像）と新規カテゴリ画像（サポート画像）間でAttentionを使用して学習する方法。もう一つはエピソード学習の考えをさらに推し進め、少数点学習に対するメタ学習アプローチを提案している。
• 本論文のモデルは、プロトタイプベクトル（各クラスを代表する埋め込み空間のベクトル）を基に分類を行う。プロトタイプベクトルをニューラルネットワークで作成する。
• モデルで用いられる基礎的な距離関数を分析し、ユークリッド距離がより一般的に用いられるコサイン類似度を大きく上回ることから、距離の選択が重要であることを経験的に見出した。

手法

モデル

生データは$D$次元データで、クラスは$K$個であるとする。
学習パラメータ$\phi$を持つ表現器$f_\phi$を用いて得られた特徴$f_\phi:\mathbb{R}^D\rightarrow \mathbb{R}^M$をクラス別に平均をとることでプロトタイプベクトルを作成する。

\boldsymbol{c}_k = \frac{1}{|S_k|}\sum_{(\boldsymbol{x}_i, y_i)\in S_k} f_\phi(\boldsymbol{x}_i)

距離関数$d:\mathbb{R}^M \times \mathbb{R}^M \rightarrow [0,\infty)$が与えられれば、ソフトマックス関数で各クラスへの分類確率が得られる。

p_\phi(y=k|\boldsymbol{x}) = \frac{\exp(-d(f_\phi(\boldsymbol{x}), \boldsymbol{c}_k))}{\sum_j \exp(-d(f_\phi(\boldsymbol{x}), \boldsymbol{c}_j))}

学習の目的関数は負の対数尤度$J(\phi)=-\log p_\phi (y=k|\boldsymbol{x})$とする。

学習のアルゴリズムは下図の通り。

さっくりアルゴリズムを説明すると、

• 各クラス別にデータをサンプル、それぞれ平均をとって$\boldsymbol{c}_k$を計算。
• 残りのデータから新たに各クラス別にデータをサンプルし、損失$J$を計算。
• オプティマイザにSGDを使用して、損失をbackwardして$\phi$を更新。
• 以上を繰り返す。

このアルゴリズムで、各データの埋め込み空間での表現がプロトタイプベクトルを重心にして集まってくる。

混合分布推定としてのprototypical networks

距離関数のクラスとして、regular Bregman divergences を考える。

d_\varphi(\boldsymbol{z}, \boldsymbol{z}')=\varphi(\boldsymbol{z})−\varphi(\boldsymbol{z}')−(\boldsymbol{z}−\boldsymbol{z}')^\top ∇\varphi(\boldsymbol{z}')

$\varphi$は任意の微分可能な凸関数で、$\varphi(\boldsymbol{z})=|\boldsymbol{z}|^2$とすれば二乗ユークリッド距離、$\varphi(\boldsymbol{z})=\boldsymbol{z}^\top \Sigma^{-1} \boldsymbol{z}$とすればマハラノビス距離になる（参考）。

キュムラント関数$\psi$の指数型分布族はregular Bregman divergencesで書ける。

p_\psi(\boldsymbol{z}|\boldsymbol{\theta}) = \exp(\boldsymbol{z}^\top \boldsymbol{\theta} - \psi(\boldsymbol{\theta})-g_\psi(\boldsymbol{z})) 
= \exp(-d_\varphi(\boldsymbol{z}, \boldsymbol{\mu}(\boldsymbol{\theta}))- g_\psi(\boldsymbol{z}))

パラメータ$\boldsymbol{\Gamma}=\{\boldsymbol{\theta}_k, \pi_k \} _{k=1}^{K}$を持つ混合分布は次のように書ける。

p(\boldsymbol{z}|\boldsymbol{\Gamma}) = \sum_k \pi_k\exp(-d_\varphi(\boldsymbol{z}, \boldsymbol{\mu}(\boldsymbol{\theta}_k))- g_\psi(\boldsymbol{z}))

ラベルされていないデータ$\boldsymbol{z}$がクラス$y$に割り当てられる確率は次のようになる。

p(y=k|\boldsymbol{z}) = \frac{\pi_k\exp(-d_\varphi(\boldsymbol{z}, \boldsymbol{\mu}(\boldsymbol{\theta}_k)))}{\sum_j \pi_j\exp(-d_\varphi(\boldsymbol{z}, \boldsymbol{\mu}(\boldsymbol{\theta}_j)))}

これよりprototypical networksは$f_\phi(\boldsymbol{x})=\boldsymbol{z}$、$ \boldsymbol{c}_k=\boldsymbol{\mu}(\boldsymbol{\theta}_k)$ とした混合分布推定に対応している。また、距離関数の選択は、埋め込み空間におけるクラスを条件付けた時のデータ分布のモデリングを仮定することに対応している。

線形モデルとしての解釈

prototypical networksの距離関数をユークリッド二乗距離にしてみる。つまり、埋め込み空間の分布がガウス分布であることを仮定する。

\begin{aligned}-|f_\phi(\boldsymbol{x}) - \boldsymbol{c}_k|^2  
&= -f_\phi(\boldsymbol{x})^\top f_\phi(\boldsymbol{x}) +2\boldsymbol{c}_k^\top f_\phi(\boldsymbol{x}) -\boldsymbol{c}_k^\top\boldsymbol{c}_k \\
&= (\mathrm{independent} \ k) +\boldsymbol{w}_k^\top f_\phi(\boldsymbol{x}) +b_k, \ \mathrm{where} \ \boldsymbol{w}_k=2\boldsymbol{c}_k, b_k=-\boldsymbol{c}_k^\top\boldsymbol{c}_k 
\end{aligned}

第一項は$k$に依存しないので、ソフトマックス関数で落ちる。第二項と第三項は線形モデルの形になっている。

※ abeTコメント：これはFC層が一層のファインチューニングの形式になっている。つまり、新規クラスに対するprototypical networksアルゴリズムを実行して$\phi$をチューンすることは、FC層を一層追加してファインチューニングをすることと同じ？

ネットワークの訓練設定

マッチングネットワークはコサイン距離を用いてマッチングネットワークを適用している。しかし、プロトタイプネットワークとマッチングネットワークの両方において、どのような距離も許容され、二乗ユークリッド距離を用いることで、両者の結果を大きく改善できることを見いだした。これは主にコサイン距離がBregman divergencesでないため、混合分布推定との等価性が成り立たないためと推測される。

学習用$N_c$はホールドアウトバリデーションセットで調整される。
訓練時とテスト時の$N_S$、すなわち「ショット」を一致させるかどうかだが、プロトタイプのネットワークでは、通常、同じ「ショット」数で訓練とテストを行うことが最善であることがわかった。

Zero-Shot Learning

ゼロショット学習の場合はメタデータベクトル$\boldsymbol{v}_k$を与え、単純にメタデータベクトルとの距離で分類を行う。

※abeTコメント：新規クラスを”学習せず”、現在のネットワークで埋め込むだけということかな？

評価

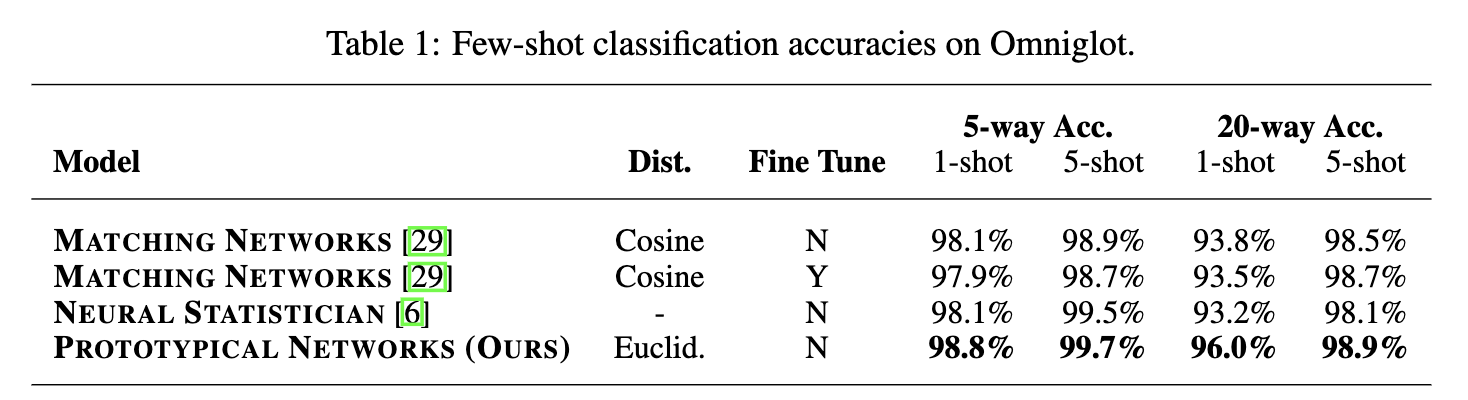
OmniglotとminiImageNetでSOTAを達成。その他は省略。

まとめと感想

• ニューラルネットワークを特徴空間への埋め込み器として利用したクラスタリングアルゴリズム。後の距離学習につながるテクニック。
• 後にファインチューニングの非常にシンプルな改良によって、ファインチューニングでも同程度の性能が得られることが分かっている（ https://arxiv.org/abs/1904.04232 ）。※ただ、後の論文はバイアス項が抜けており、厳密な比較ではないように思える。normalizationが効いている可能性はある。なぜならば新規クラスは学習が足りずnormalizeが十分でない可能性があるため。