概要
ピンホールカメラモデルを通して、3次元の座標がどのように画像の座標と対応するかを紹介します。また、3次元の座標と画像の座標を対応させるのに必要なパラメータの求め方をカメラキャリブレーションを通して紹介します。
ピンホールカメラモデル
ピンホールカメラモデルは、カメラの単純なモデルであり、物体の位置や向きを推定するために広く使用されています。このモデルは、3D復元、カメラキャリブレーション、画像処理、およびロボットビジョンなどのアプリケーションで使用されます。
ピンホールカメラモデルでは、座標系がたくさん出てくるので、注意しながら進めます。多くの書籍では3つの座標系を考えますが、より厳密に次の4つの座標系を考えることにします。
- ワールド座標系(3次元座標)
- カメラ座標(カメラの中心を原点にとった3次元座標)
- 画像平面座標(カメラ座標のZ軸がカメラの焦点距離となるX-Y平面の2次元座標)
- 画像座標(撮像素子で記録された画像の2次元座標)
まず、任意に設定した3次元の座標をワールド座標系と呼びます。添え字に$w$をつけます。次に、ピンホールカメラモデルでは、物体からの光線がピンホールを通過し、画像平面に投影されます。カメラのレンズ中心を原点とし、光軸方向をZ軸にとったカメラ座標系です。添え字に$c$をつけます。カメラ座標のZ軸がカメラの焦点距離となるX-Y平面を画像平面座標と呼びます。

カメラ座標上の点$\boldsymbol{M}_c$とカメラ座標系の原点$O_c$を結んで、画像平面座標へ写像します。この射影は次の式で表せます。
\begin{align}
x &= \frac{f}{z_c}x_c \\
y &= \frac{f}{z_c}y_c \\
\end{align}
これは行列の積で表現できます。
\begin{align}
s
\begin{pmatrix}
x\\
y\\
1
\end{pmatrix}
=
\begin{pmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0& 1& 0 \\
\end{pmatrix}
\begin{pmatrix}
x_c \\
y_c \\
z_c \\
1
\end{pmatrix}
\end{align}
.
座標を1次元拡張し、値を1としたベクトルを用いることで計算が楽になります。これを同次座標と呼びます。同次座標のベクトルにはチルダを付けることにします。すると射影の式は次の式になります。
s \tilde{\boldsymbol{m}}_s = Q \tilde{\boldsymbol{M}}_c.
ここで、$Q$は次のように定義します。
Q =
\begin{pmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0& 1& 0 \\
\end{pmatrix},
ところで、同次座標を使用するとワールド座標とカメラ座標の変換は次の式で表せます。
\tilde{\boldsymbol{M}}_c = D \tilde{\boldsymbol{M}}_w \\
D =
\begin{pmatrix}
R & \boldsymbol{t} \\
\boldsymbol{0}^\top & 1
\end{pmatrix}
$R$は$3\times3$の回転行列、$\boldsymbol{t}$は3次元の平行移動ベクトルです。以上でワールド座標系とカメラ座標系、画像平面座標の対応関係が得られました。
次に画像座標系を考えます。画像座標系は実際に撮影された画像の座標系で、これは一般に画像平面座標に一致しません。光軸と画像座標の原点が一致するとは限りませんし、撮像素子によってはX軸とY軸のスケールが異なります。また、画像座標のX軸とY軸は直行しているとは限りません。
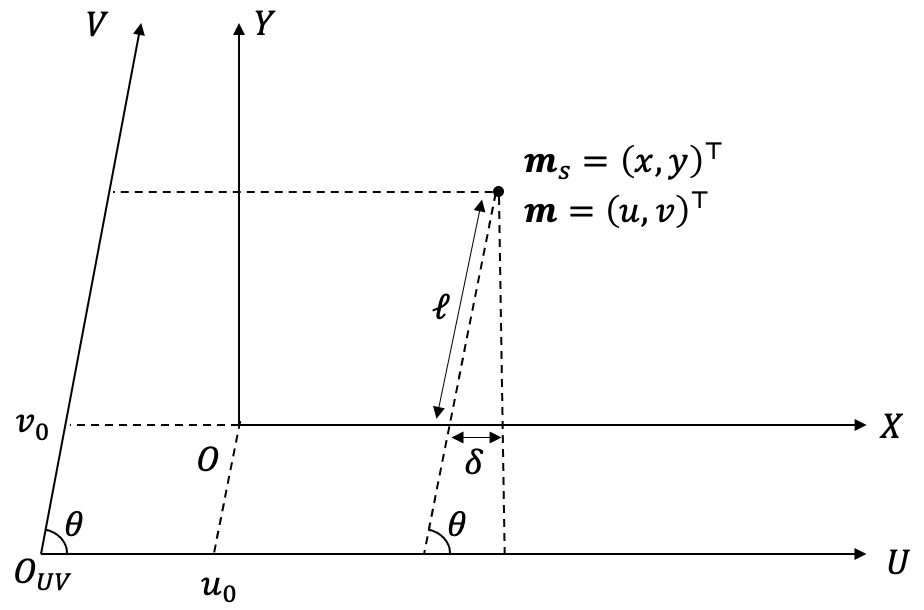
画像平面座標と画像座標の対応がどのように表されるか考えます。まず、カメラ座標の設定を思い出すと、Z軸は光軸に合わせしましたが、X軸とY軸については制約がなかったので、2次元回転の不定性が残っています。そこで、この不定性を使用して、カメラ座標のX軸(すなわち画像平面座標のX軸)と画像座標のX軸が平行になるようにします。画像平面座標のスケールに対して、画像座標のスケールはX軸Y軸それぞれ$(k_x, k_y)$倍とします。図から次の関係が読み取れます。
\begin{align}
u &= k_u x - k_u y \cot\theta + u_0 \\
v &= k_v \frac{y}{\sin\theta} +v_0
\end{align}
同次座標を用いて次のように表せます。
\begin{align}
\tilde{\boldsymbol{m}} =
\begin{pmatrix}
k_x & - k_x \cot\theta & u \\
0 & \frac{k_y}{\sin\theta} & v \\
0 & 0& 1 \\
\end{pmatrix}
\tilde{\boldsymbol{m}}_s
\end{align}
さらに画像座標とカメラ座標の関係を求めると次のようになります。
\begin{align}
s \tilde{\boldsymbol{m}}
&=
\begin{pmatrix}
k_u & - k_u \cot\theta & u_0 \\
0 & \frac{k_v}{\sin\theta} & v_0 \\
0 & 0& 1 \\
\end{pmatrix}
Q \tilde{\boldsymbol{M}}_c \\
&=
\begin{pmatrix}
fk_u & - fk_u \cot\theta & u_0 & 0 \\
0 & \frac{fk_v}{\sin\theta} & v_0 & 0 \\
0 & 0& 1 & 0\\
\end{pmatrix}
\tilde{\boldsymbol{M}}_c
\end{align}
この5つのパラメータ$fk_u, fk_u, \theta, u_0, v_0$ をカメラの内部パラメータと呼びます。カメラの内部パラメータには、焦点距離、撮像素子の形状、および画像中心点の座標の情報が含まれます。行列の前3行3列を取り出した行列を内部行列と呼び、$A$と表します。
ワールド座標と画像座標の対応は次のように表せます。
\begin{align}
s \tilde{\boldsymbol{m}}
&=
\begin{pmatrix}
A & \boldsymbol{0}
\end{pmatrix}
\begin{pmatrix}
R & \boldsymbol{t} \\
\boldsymbol{0}^\top & 1
\end{pmatrix}
\tilde{\boldsymbol{M}}_w \\
&=
A
\begin{pmatrix}
R & \boldsymbol{t}
\end{pmatrix}
\tilde{\boldsymbol{M}}_w
\end{align}
$(R, \boldsymbol{t})$を外部パラメータと呼びます。
カメラキャリブレーション
カメラキャリブレーションとは、カメラの内部パラメータと外部パラメータを決定するプロセスです。内部パラメータは、カメラ自身の光学特性を含みます。外部パラメータは、カメラの位置と向きを表し、位置、回転を含みます。
カメラキャリブレーションにより、画像に対する正確なカメラ位置や向きがわかるため、3D復元、オブジェクト追跡、および拡張現実などのアプリケーションで使用されます。
カメラの内部パラメータと外部パラメータを次のように表すことにします。
\begin{align}
P =
A
\begin{pmatrix}
R & \boldsymbol{t}
\end{pmatrix}
\end{align}
$P$を透視投影変換行列と呼びます。スケール変換の不定性があるため、$p_{34}=1$として、スケールを固定しました。
画像の座標と3次元の座標の対応から$P$の値を求めることができます。ワールド座標と画像座標の対応は次のように表せます。
\begin{align}
s
\begin{pmatrix}
u \\
v \\
1
\end{pmatrix}
=
P
\begin{pmatrix}
x_w \\
y_w \\
z_w \\
1
\end{pmatrix}
=
\begin{pmatrix}
p_{11} & p_{12} & p_{13} & p_{14} \\
p_{21} & p_{22} & p_{23} & p_{24} \\
p_{31} & p_{32} & p_{33} & 1 \\
\end{pmatrix}
\begin{pmatrix}
x_w \\
y_w \\
z_w \\
1
\end{pmatrix}
\end{align}
.
解いて$s$を消すと3次元座標から2次元座標への写像が得られます。
\begin{align}
u = \frac{p_{11}x_w + p_{12}y_w + p_{13}z_w + p_{14}}{p_{31}x_w + p_{32}y_w + p_{33}z_w + 1} \\
v = \frac{p_{21}x_w + p_{22}y_w + p_{23}z_w + p_{24}}{p_{31}x_w + p_{32}y_w + p_{33}z_w + 1}
\end{align}
この式から独立な2本の式を立てられるので、自由度11の$P$を求めるには、6つ以上の対応点が分かればよいです。
\begin{pmatrix}
x_w & y_w & z_w & 1 & 0 & 0 & 0 & 0 & -u x_w & -u y_w & -u z_w \\
0 & 0 & 0 & 0 & x_w & y_w & z_w & 1 & -v x_w & -v y_w & -v z_w
\end{pmatrix}
\begin{pmatrix}
p_{11} \\
p_{12} \\
p_{13} \\
p_{14} \\
p_{21} \\
p_{22} \\
p_{23} \\
p_{24} \\
p_{31} \\
p_{32} \\
p_{33}
\end{pmatrix}
=
\begin{pmatrix}
u \\
v \\
\end{pmatrix}
.
画像間の対応する点が$N$個ある場合、記号を整理して次のように書きます。
X = \begin{pmatrix}
x_w^1 & y_w^1 & z_w^1 & 1 & 0 & 0 & 0 & 0 & -u^1 x_w^1 & -u^1 y_w^1 & -u^1 z_w^1 \\
0 & 0 & 0 & 0 & x_w^1 & y_w^1 & z_w^1 & 1 & -v^1 x_w^1 & -v^1 y_w^1 & -v^1 z_w^1 \\
\cdots \\
\cdots \\
x_w^{N} & y_w^{N} & z_w^{N} & 1 & 0 & 0 & 0 & 0 & -u^{N} x_w^{N} & -u^{N} y_w^{N} & -u^{N} z_w^{N} \\
0 & 0 & 0 & 0 & x_w^{N} & y_w^{N} & z_w^{N} & 1 & -v^{N} x_w^{N} & -v^{N} y_w^{N} & -v^{N} z_w^{N}
\end{pmatrix}, \\
\boldsymbol{y} = \begin{pmatrix}
u^{1} \\
v^{1} \\
\cdots \\
\cdots \\
u^{N} \\
v^{N} \\
\end{pmatrix},
\boldsymbol{p} = \begin{pmatrix}
p_{11} \\
p_{12} \\
p_{13} \\
p_{14} \\
p_{21} \\
p_{22} \\
p_{23} \\
p_{24} \\
p_{31} \\
p_{32} \\
p_{33}
\end{pmatrix}
.
以上の記号を用いて透視投影変換は次のようになります。
\begin{align}
X \boldsymbol{p} = \boldsymbol{y}
\end{align}
$Q$を求めたら、$A$が上三角行列であることを利用してRQ分解を行うことにより、$A$と$(R \ \boldsymbol{t})$に分解できます。
実装
今回は自前で画像を用意しました。画像に丸で示した6点の座標を対応させて、カメラパラメータを推定します。

"""
Copyright 2023 ground0state
Released under the MIT license
"""
import cv2
import numpy as np
import scipy
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
def _create_data_matrix(object_point, image_point):
xw, yw, zw = object_point
u, v = image_point
matrix = [
[xw, yw, zw, 1, 0, 0, 0, 0, -u * xw, -u * yw, -u * zw],
[0, 0, 0, 0, xw, yw, zw, 1, -v * xw, -v * yw, -v * zw],
]
return matrix, [u, v]
def _estimate_projection(object_points, image_points, verbose=0):
X, y = zip(*[_create_data_matrix(src_pt, dst_pt)
for src_pt, dst_pt in zip(object_points, image_points)])
X = np.concatenate(X).astype(np.float32)
y = np.concatenate(y).astype(np.float32)
estimator = LinearRegression(
fit_intercept=False).fit(X, y)
if verbose >= 1:
print("estimator score:", estimator.score(X, y))
p = estimator.coef_.copy()
p = np.concatenate([p, [1]])
P = p.reshape(3, 4)
return P
def find_projection_matrix(object_points, image_points, verbose=0):
P = _estimate_projection(
object_points, image_points, verbose=verbose)
return P
def find_projection_matrix_opencv(object_points, image_points):
X, y = zip(*[_create_data_matrix(src_pt, dst_pt)
for src_pt, dst_pt in zip(object_points, image_points)])
X = np.concatenate(X).astype(np.float32)
y = np.concatenate(y).astype(np.float32)
_, p = cv2.solve(X, y, flags=cv2.DECOMP_SVD)
p = np.concatenate([p.reshape(-1), [1]])
P = p.reshape(3, 4)
return P
def apply_projection(object_points, q):
xw, yw, zw = object_points
vec = np.array([xw, yw, zw, 1])
scaled_image_point = q.dot(vec)
x, y = (scaled_image_point/scaled_image_point[2])[:2]
return [x, y]
def decompose_projection_matrix(P, verbose=0):
"""
投影行列を分解し、カメラのキャリブレーション行列、回転行列、およびワールド座標におけるカメラ中心を取得します。
Parameters
----------
P : ndarray
分解する投影行列。形状は (3, 4) である必要があります。
verbose : int, optional
冗長モード。verboseが1以上の場合、分解の残差平方和(RMSE)が表示されます。デフォルトは0。
Returns
-------
A : ndarray
カメラのキャリブレーション行列。形状は (3, 3) です。
R : ndarray
カメラの回転行列。形状は (3, 3) です。
T : ndarray
ワールド座標におけるカメラ中心。形状は (3,) です。
Notes
-----
この関数は、投影行列をキャリブレーション行列と回転行列に分解します。さらに、キャリブレーション行列を用いて変換行列を分解し、
ワールド座標におけるカメラ中心を取得します。これは3Dコンピュータビジョンで頻繁に用いられる処理で、カメラの内部パラメータ(キャリブレーション行列)
と外部パラメータ(回転行列と並進ベクトル)を取得することで、3次元空間における物体の位置やカメラの位置を理解することができます。
Rはカメラ座標の各軸の方向を表すカメラ座標の単位ベクトルをワールド座標で見た時のベクトルを行ベクトルとして並べたものです。したがって、
Rは直行行列とは限りません。なぜならば、一般にワールド座標とカメラ座標の単位長が異なるからです。このRは単位長を変換するスケール変換を含んでおり、
このスケール倍分だけ直交行列からずれます。
Tはワールド座標で見た時の、ワールド座標原点からカメラ座標原点へのベクトルです。tはカメラ座標で見た時の、
カメラ座標原点からワールド座標原点へのベクトルです。
Rとtをカメラの外部パラメータと呼びます。
Examples
--------
>>> import numpy as np
>>> q = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
>>> A, R, T = decompose_projection_matrix(q)
"""
AR, At = P[:, :3], P[:, 3]
A, R = scipy.linalg.rq(AR)
# Normalize
R = R * A[2, 2]
A /= A[2, 2]
# Sign of determinant should be positive, if not then negate calibration matrix
if np.linalg.det(A) < 0:
A *= -1
R *= -1
# Decompose the transformation matrix to retrieve camera center in world coordinates
t = np.dot(np.linalg.inv(A), At)
if verbose >= 1:
outer_param = np.concatenate([R, t.reshape(-1, 1)], axis=1)
residual = mean_squared_error(
(A @ outer_param).reshape(-1),
P.reshape(-1),
squared=False
)
print("Decomposition RMSE:", residual)
T = -np.linalg.inv(R)@t
return A, R, T
def decompose_projection_matrix_opencv(P):
A, R, T, _, _, _, _ = cv2.decomposeProjectionMatrix(P)
R = R * A[2, 2]
A = A / A[2, 2]
T = T.reshape(-1)
T = T / T[-1]
T = T[:3]
return A, R, T
def main():
# def main():
# (x, y, z) [cm]
object_points = [
[0, 0, 0],
[6.5, 0, 0],
[0, 6.5, 0],
[0, 0, 10],
[6.5, 0, 10],
[0, 6.5, 10]
]
# (x, y) [px]
image_points = [
[720, 1773],
[1317, 1356],
[292, 1245],
[741, 954],
[1467, 561],
[216, 441],
]
P = find_projection_matrix(object_points, image_points, verbose=1)
P_ = find_projection_matrix_opencv(object_points, image_points)
rmse = np.sqrt(np.mean((P - P_)**2))
rmse = mean_squared_error(P.reshape(-1), P_.reshape(-1), squared=False)
print("透視投影行列をOpenCVと比較 RMSE:", rmse)
new_object_point = [6.5, 6.5, 10]
new_image_point = apply_projection(new_object_point, P_)
img = cv2.imread("sample.jpg", cv2.IMREAD_COLOR)
img_pointed = img.copy()
for pt in image_points:
img_pointed = cv2.circle(img_pointed,
center=list(map(int, pt)),
radius=20,
color=(0, 0, 255),
thickness=3,
lineType=cv2.LINE_4,
shift=0)
cv2.imwrite("points.jpg", img_pointed)
new_img_pointed = cv2.circle(img,
center=list(map(int, new_image_point)),
radius=20,
color=(0, 0, 255),
thickness=3,
lineType=cv2.LINE_4,
shift=0)
cv2.imwrite("new_points.jpg", new_img_pointed)
A, R, T = decompose_projection_matrix(P, verbose=1)
A_, R_, T_ = decompose_projection_matrix_opencv(P)
A_rmse = mean_squared_error(A.reshape(-1), A_.reshape(-1), squared=False)
R_rmse = mean_squared_error(R.reshape(-1), R_.reshape(-1), squared=False)
T_rmse = mean_squared_error(T.reshape(-1), T_.reshape(-1), squared=False)
print("行列分解をOpenCVと比較 A_rmse:", A_rmse)
print("行列分解をOpenCVと比較 R_rmse:", R_rmse)
print("行列分解をOpenCVと比較 t_rmse:", T_rmse)
print(A)
if __name__ == "__main__":
main()
奥の角の3次元座標を画像に写像したのが下の画像です。

Reference
中村恭之, 小枝正直, 上田悦子,『OpenCVによるコンピュータビジョン・機械学習入門』, 講談社サイエンティフィク, 2017.