Info
- タイトル:OS2D: One-Stage One-Shot Object Detection by Matching Anchor Features
- カンファ:ECCV2020
- 著者:Anton Osokin, Denis Sumin, Vasily Lomakin
- 論文:https://arxiv.org/abs/2003.06800
- プロジェクトページ:https://github.com/aosokin/os2d
概要
- ワンショット物体検出タスクで、局所化と認識を同時に行う1ステージの手法を提案。
- すべての構成要素は微分可能であり、エンドツーエンドの学習が可能。
- いくつかの困難な領域(小売製品、3Dオブジェクト、建物、ロゴ)で実験的に評価した結果、未知のクラスを検出でき(例えば、食料品で訓練した場合、歯磨き粉)、いくつかのベースラインを大幅に上回る性能を持つことが示された。
背景
- 物体検出に対する典型的アプローチは大規模なアノテーション付きデータセットに対する畳み込みニューラルネットワーク(CNN)の学習で構成されている。
- このようなデータセットの収集と注釈付けは、このようなシステムを展開する際の大きなコストとなることが多く、対象となるクラスのリストが大きい場合や時間と共に変化する場合にボトルネックとなる。例えば、スーパーマーケットの棚に並ぶ小売商品のドメインでは、入手可能な商品の品揃えや外観が徐々に変化するため(例えば、毎月10%の商品が変わることもある)、データセットの収集と維持が困難である。大規模なアノテーション付き学習セットの要件を緩和することで、技術の適用が容易になる。
- 提案手法では、1回のデモで定義された物体を検出するタスク(ワンショット物体検出)を考える。
- ワンショット物体検出は、1つの顕著な例外(人物認識を含む人間の顔検出)を除いて、実質的にあまり研究されていない。人間の顔はよく定義されたオブジェクトで、初見の顔に対してうまく機能することが知られている。一方で、一般物体クラスでは十分な汎化性が得られないという問題がある。
- 一般物体クラスに対するOne-Shot Object Detection手法は、領域提案ネットワークと、認識のための埋め込みブロックの2つの異なるステージを持つ。ネットワーク重みのファインチューニングを行うことで2つのステージを連携させているが、テストステージでは、クラスに依存しない物体提案に頼っている、つまり対象クラス画像に依存しない領域提案ネットワークを使用している。最近では、対象クラス画像を用いる領域提案ネットワークが提案されている。
- 本論文では1ステージの検出器 OS2D を構築する。提案手法は記述子マッチングとそれに続く幾何学的検証に基づく古典的なパイプラインに似ている。
- 疎なマッチングの代わりに密なマッチング
- ハンドクラフトの局所特徴の代わりに学習
- RANSACの代わりにフィードフォワード幾何変換モデルを利用
- 提案手法の特徴は、一般的な物体を定義することなく(その代わりに、優れた特徴記述子と変換モデルが必要)、検出と認識を共同で行うことである。
- 提案手法をいくつかの領域(GroZi-3.2kデータセット[8]に基づく小売商品、INSTREデータセット[44]に基づく日常の3D物体、建物、ロゴ)に適用した。すべての設定において、複数のベースラインよりも大きく優れていた。本手法とベースラインのコードおよび収集した全てのデータはオンラインで入手可能である。
ベースラインと提案手法の比較は下図。ベースラインは物体クラスに依存しない物体を検出するステージと分類を行うステージで構成されている。ベースラインはターゲット画像を知らないため、ターゲット物体を分離して領域提案してしまっている。一方提案手法は1つのオブジェクトとして検出に成功している。

手法
ネットワーク

- クエリ画像とクラス画像に対して、backboneで特徴を抽出$\left( f_{kl}^\mathcal{A} \in \mathbb R ^{h^\mathcal{A}\times w^\mathcal{A}\times d}, f_{pq}^\mathcal{C} \in \mathbb R ^{h^\mathcal{C}\times w^\mathcal{C}\times d}\right)$。クエリ画像とクラス画像からシャム法、すなわち同一のパラメータを持つネットワークで特徴を抽出することが非常に重要。
- クラス画像特徴はdifferentiable bilinear resamplingで固定サイズ$f_{pq}^\mathcal{T} \in \mathbb R ^{h^\mathcal{T}\times w^\mathcal{T}\times d}$に変える。単純なリサイズだとアスペクト比が変わって見た目が歪み、誤ったクラスとしてしまう(例:瓶が縮んで缶になってしまう)。そのため、微分可能なリサンプリング手法を使用する。
- クエリ画像特徴とクラス画像特徴で相関を計算する$\left(c\in\mathbb R ^{h^\mathcal{A}\times w^\mathcal{A}\times h^\mathcal{T} \times w^\mathcal{T}}\right)$。相関はコサイン類似度で算出し、テンソルを$h^\mathcal{T}\times w^\mathcal{T}\rightarrow h^\mathcal{T}w^\mathcal{T}$とreshapeする$\left(\tilde c\in\mathbb R ^{h^\mathcal{A}\times w^\mathcal{A}\times \left(h^\mathcal{T}w^\mathcal{T}\right)}\right)$。
- 相関テンソルをTransformNetと名付けたネットワークに入力して、$h^\mathcal{A}\times w^\mathcal{A}\times P$に変換する。TransformNetは特徴マップのアフィン変換のパラメータを回帰予測するネットワークである1。TransformNetの最初のConvのカーネルサイズは$h^\mathcal{T}\times w^\mathcal{T}$とすることが重要。

画像はTransformNetの元となった論文1の図
- $h^\mathcal{A}\times w^\mathcal{A}\times P$はクエリ画像の特徴マップのグリッド単位のアフィン変換を表している。しかし欲しいのはクラス画像の特徴マップのグリッド単位のアフィン変換であり、またクラス画像とクエリ画像のグリッドの対応も考慮する必要がある。そこで、「クエリ画像の特徴マップの各グリッドに対する、クラス画像の特徴マップの各グリッドの座標位置」を表すテンソル$g\in \mathbb R ^{h^\mathcal{A}\times w^\mathcal{A}\times h^\mathcal{T} \times w^\mathcal{T}\times 2}$へ変換する。これをグリッドサンプラーと呼ぶ。変換パラメータの回帰ではなく、変換後のグリッド位置を直接出力するようにし、したがって出力は$(y, x)$座標値の2次元になる。
g \in \mathbb R ^{h^\mathcal{A}\times w^\mathcal{A}\times h^\mathcal{T} \times w^\mathcal{T}\times 2}, \\
G_{kl}(p,q):= (g[k,l,p,q,0], g[k,l,p,q,1])\in \mathbb R^2
- Outputs層で出力を計算する。
- クエリとクラスのマッチングスコアを計算する。スコアは既に計算したクエリ画像特徴とクラス画像特徴の相関$c$をスコアに用いる。グリッドサンプラーで補正した位置を使用して、空間補正された相関$\hat s[k,l,p,q]:=c[g[k,l,p,q,0], g[k,l,p,q,1], p, q]$を得る。ここで、$g$は非整数なので、バイリニア補完を使用して計算する。最後に$\hat s$のクラス画像成分を平均プーリングする。このとき、グリッドの境界部分は背景を含む可能性が高く、クエリ画像とクラス画像の背景相関は不要なので、グリッド境界部分は計算から除く。以上より、その位置がどの程度検出される可能性があるかを示すスコスコア$s \in \mathbb R ^{h^\mathcal{A}\times w^\mathcal{A}\times 1}$を得る。
- グリッドテンソル$g$の3次元と4次元の最大値と最小値を取ることにより、ボックスを得る。
損失関数
\begin{aligned}
\mathcal L_{\mathrm{loc}} &= \frac{1}{n_{\mathrm{pos}}} \sum_{i:t_i=1}\ell_{\mathrm{loc}} (\boldsymbol x_i, \boldsymbol y_i) \\
\mathcal L_{\mathrm{rec}} &= \frac{1}{n_{\mathrm{pos}}} \sum_{i:t_i=1}\ell_{\mathrm{rec}}^{\mathrm{pos}}(s_i)^2
+\frac{1}{n_{\mathrm{pos}}} \sum_{i:t_i=0}\ell_{\mathrm{rec}}^{\mathrm{neg}}(s_i)^2 \\
\ell_{\mathrm{loc}} (\boldsymbol x, \boldsymbol y) &= \sum_{c=1}^4 \left\{
\begin{array}{ll}
\frac{1}{2}(x_c-y_c)^2 ,& \mathrm{if}\quad|x_c-y_c| < 1 \\
|x_c-y_c| - \frac{1}{2} ,& \mathrm{otherwise}
\end{array}
\right. \\
\ell_{\mathrm{rec}}^{\mathrm{pos}}(s) &= \max(m_{\mathrm{pos}} - s,0) \\
\ell_{\mathrm{rec}}^{\mathrm{neg}}(s) &= \max(s - m_{\mathrm{neg}},0) \\
\end{aligned}
$s\in[-1,1]$は検出スコアで、positiveのときに正に、negativeのときに負になるように学習させる。$m_{\mathrm{neg}}<0,m_{\mathrm{pos}}>0$はマージンである。$\boldsymbol x, \boldsymbol y\in \mathbb R^4$はバウンディングボックスである。
バッチ内でハードネガティブマイニング(各ボックスについて検出スコアでソートして負と正の比率が最大でも3:1になるようにする)を行う。$n_{\mathrm{pos}}$は現在のバッチのpositiveの数である。positiveマージンは最初$1$にしておく。
$i$は全てのグリッド位置をループし、$(s_i,\boldsymbol x_i)$はネットワークから出力され、$(t_i,\boldsymbol y_i)$はアノテーションから与えられる。
また、上記の損失関数を少し修正したranked list lossについても実験を行った。
評価
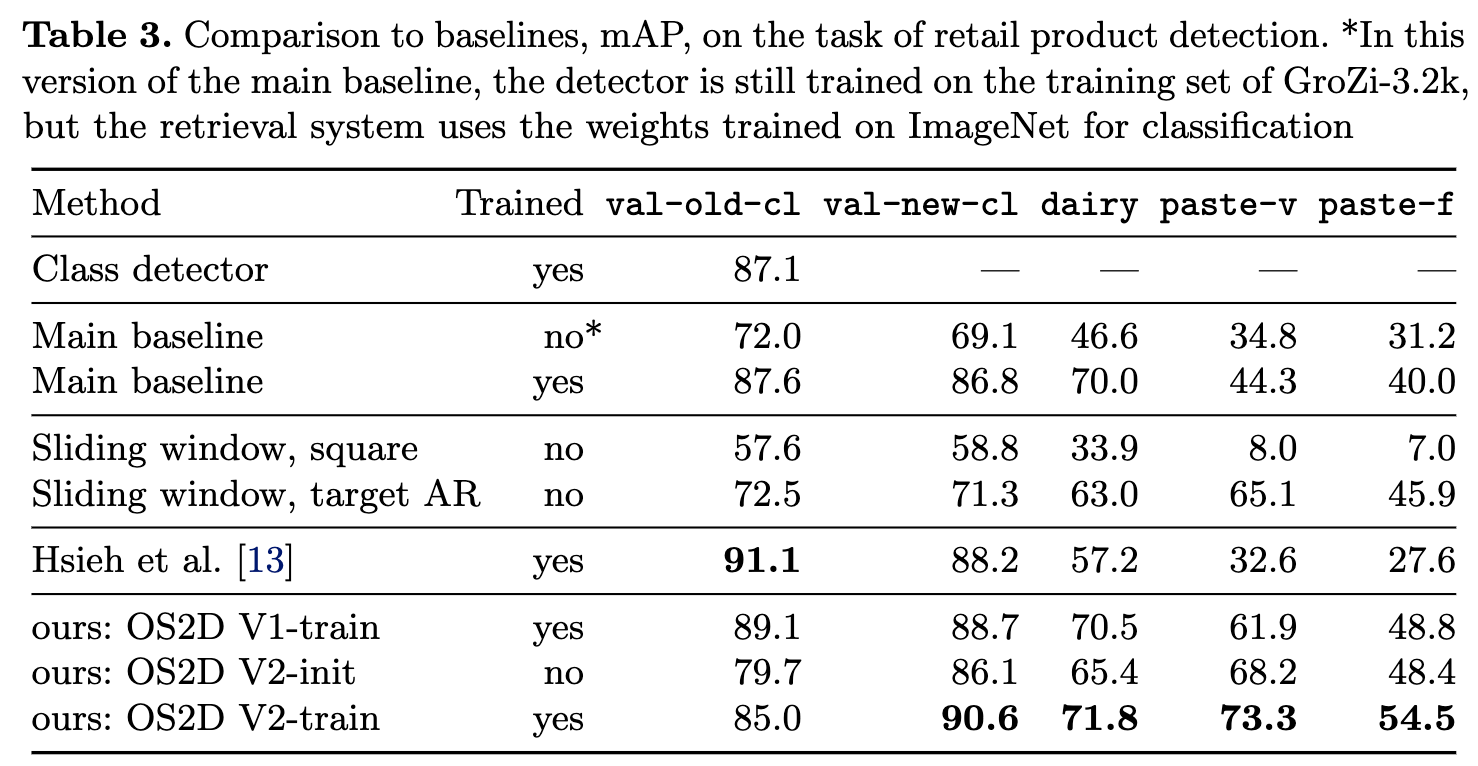
GroZi-3.2kデータセットでは既存のモデルよりも精度が良い。
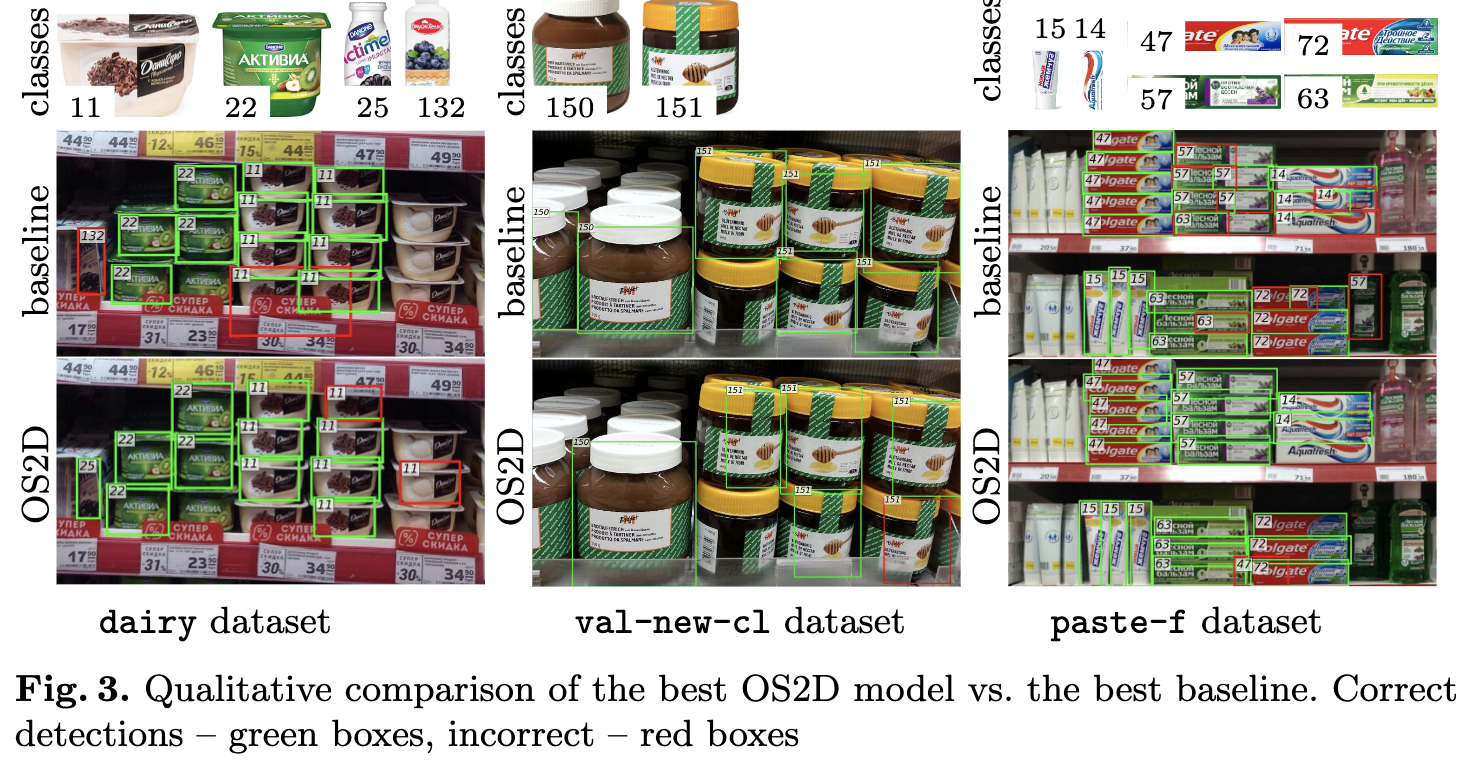
まとめ・感想
- zero-shotの割には良く検出できている印象。
- クラス画像を増やしたり、backboneの事前学習データを変えたりすることで性能が変化しそう。