これはなに?
Qiita:デジタル制御するためのソフトウェアアーキテクチャ
以前書いた記事の内容があまりにポエムなので実証編を用意しました。
今回は入力と出力の電圧が電圧源で固定されている
バックコンバータの電流制御をやってみます.
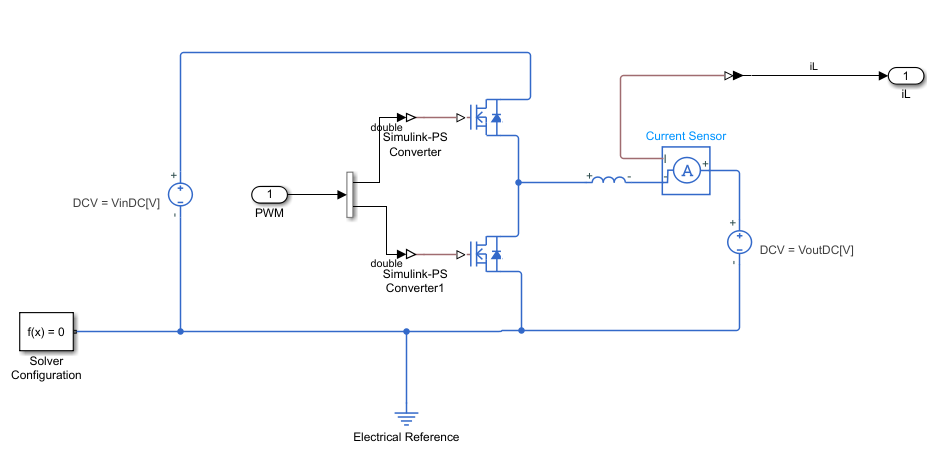
どんなモデル作ったの
こんな感じで動いておりまする。ADCのタイミングが前述の怪文書のとおりになってるのがわかるかと思います。
割り込みにおける計算時間が間に合ってるかはMILの段階では表現されてはいませんが、
離散化したパラメータを使って制御ループがスイッチングしているPlantに対して
狙った通りの応答を示すかは確認できるかと思います。
おそらくデットタイム誤差のせいでちょっと目標値にびしっと到達してませんが。
ちなみにこのモデルはGithubにアップされています。リポジトリはこちら。
https://github.com/mathworks/adc-synchronized-with-pwm
ちょっとSimulinkで作ったコンバータの動作を改めて確認。良い感じではないか。
— griffin921 (@griffin921) November 20, 2021
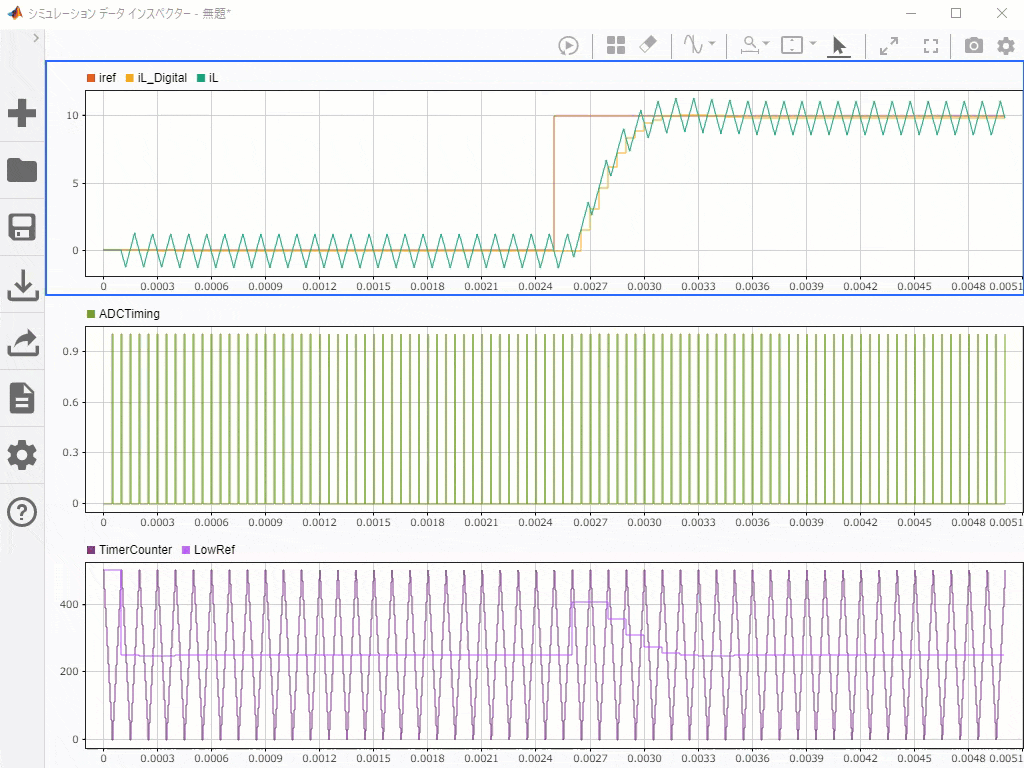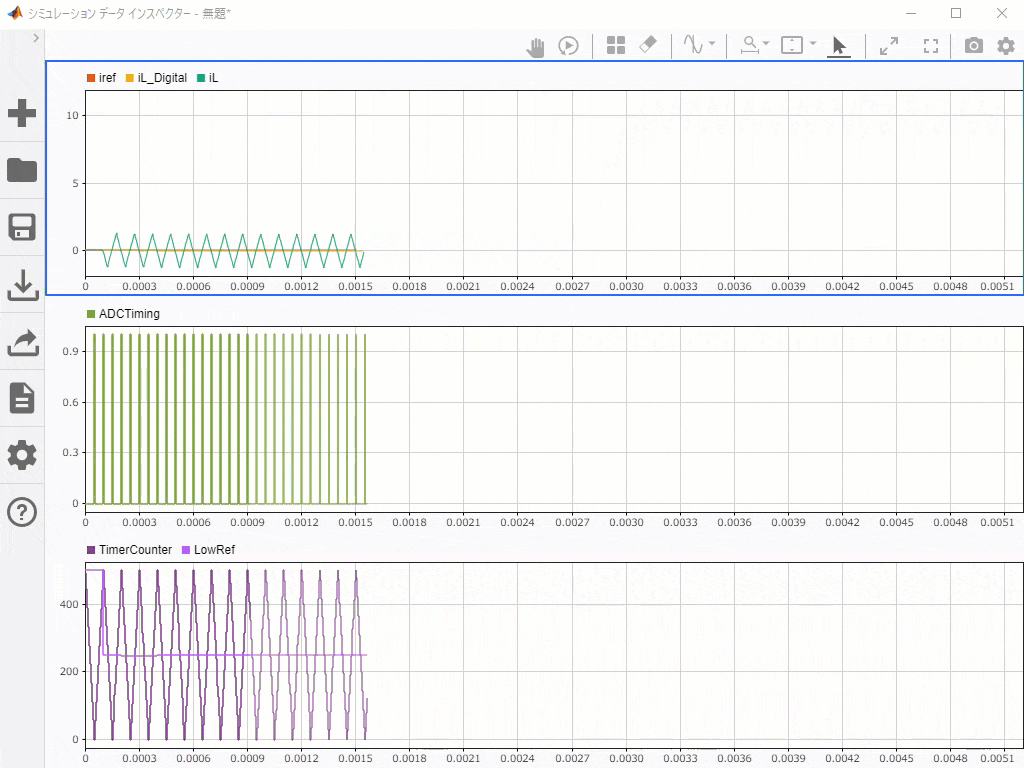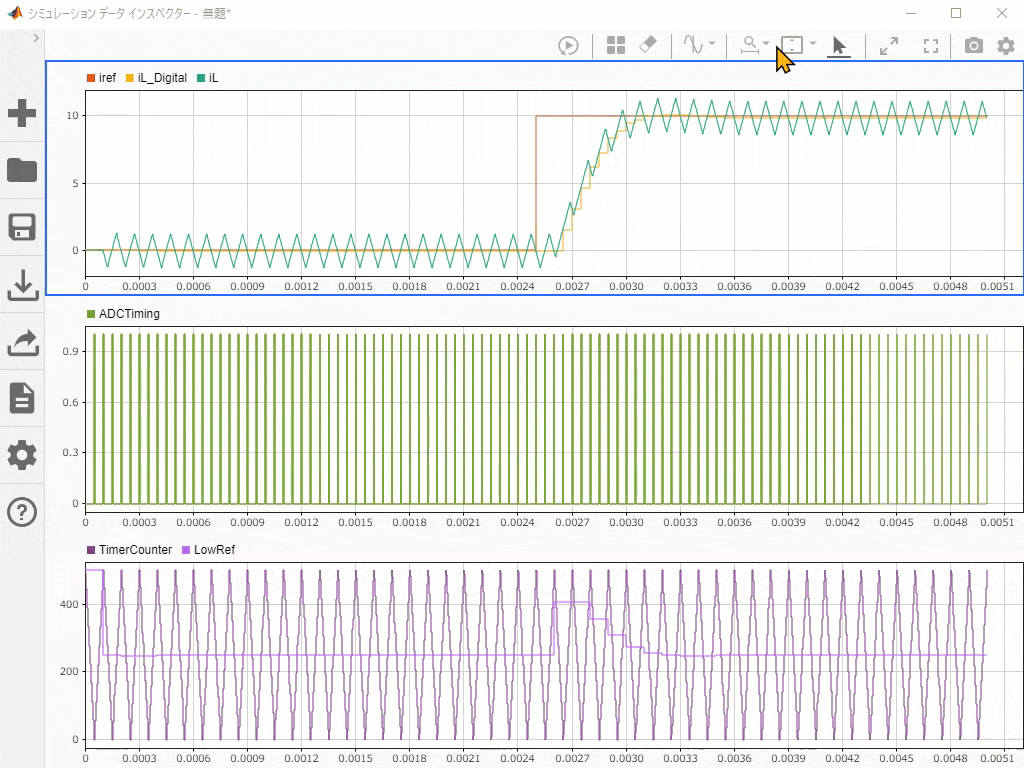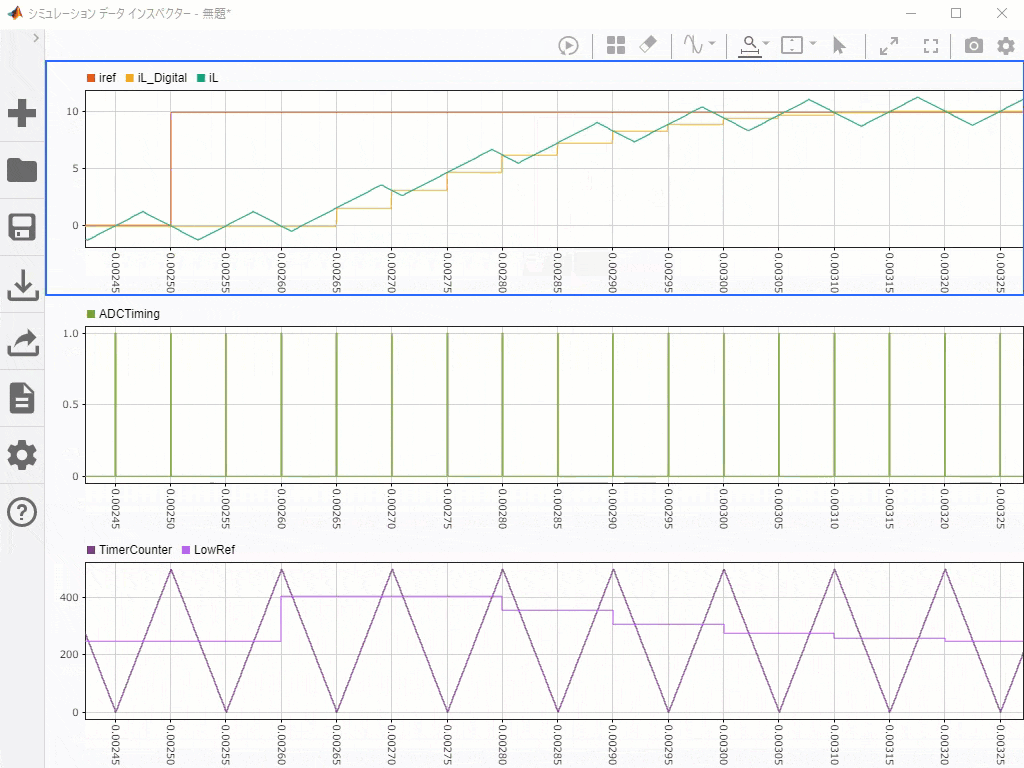
ADCの指定タイミング(キャリアの山谷)でサンプリング値が更新されており、それが電流平均値と一致している。 pic.twitter.com/4GQOViuTQh
仕様はこんな感じ
fsw = 10e3; %Hz
PWM_Resolution = 0.001;
CarrierSampleTime = 1 / fsw * PWM_Resolution;
DeadTime = 1/fsw/1000;
L = 1e-3;%[H]
RdsON_FET = 10e-3;%[Ω]
VinDC = 100;%[V]
VoutDC = 50;%[V}
制御設計はこんな感じ。
PlantはFETの直流抵抗(Rds_ON)とインダクタのLで1次遅れにみえるとしています。
%Control Design
s = tf('s');
%制御対象回路の伝達関数をモデリング
Plant = 1/(L*s + RdsON_FET);
%制御の帯域幅を設定
TargetCntF = 2*pi*500;
Tcnt = 1 / TargetCntF;
%内部モデル原理に基づきコントローラーを設計
Controller = 1 / Plant * 1 / (Tcnt * s);
%等価な伝達関数を持つPIパラメータを算出
Ti = 1/TargetCntF/RdsON_FET;
Kp = L/RdsON_FET / Ti;
PICnt = (Kp*Ti*s+1) / Ti/s;
こちらの動画で、一番下のキャリアカウンタの山谷でADCタイミングパルスが生成され(中段グラフ)、同期したサンプリングをしていることがわかる(上段グラフ)と思います。
PWM解像度ってなに?
pwmの解像度を0.1%に設定しました。
デシタル制御ではタイマーをカウンターで作ります
アナログのタイマーはとぎれのない連続な波形を作るので理想としてはどんな幅のパルスも作れます。
今回の仕様ではPWMパルス幅の最大値は
100 usec ですね。極端に言うとアナログだと dutyが0.000001 %だとちゃんとその幅のパルスが出ます。1
でもデジタルはあるクロック毎に一つずつカウントアップするので表現可能な最小時間単位はキャリアクロックに依存します。
ですから、それよりこまかいパルスはデジタル制御では基本的に出せないんです!2
この方の記事の図がわかりやすいです。
https://blog.boochow.com/article/raspberry-pi-hw-pwm-driver-2.html
PWM解像度って指定する意味あるの?
あるとおもいます。シミュレーションを何処までの細かさで表現するかということも関わってきますし、
この辺シミュレーションをする際にもシミュレーションスピードが関係してきます。
例えばこのモデルではタイマカウンターとリファレンスの大小を比較して、
PWMのパルスをHigh、Lowにするタイミングを決めてます。
このときの演算すべき最小ステップ数はPWM解像度に依存します。
モデルがいつどのタイミングでPWMを立ち上がるかは、そのモデルを動かしてみないとわかんないので、やってみるしかないです。
そのとき、安易にシミュレーションタイムステップ幅をでかくしてしまったら本来立ち上げるタイミングだった時間を逃してしまい、それが回路の動作に影響を及ぼしてしまいます。
もしPWM解像度を任意に指定していなければ、シミュレータの可変ステップソルバは一体どれだけステップ時間を荒くしてよいか見当がつかないので、誤差を小さくするにはかなり細かいステップ幅でシミュレーションを実行しないといけません。
このような動作はシミュレーションの速度低下につながるかもしれません
Simulinkではロジックによってはシミュレーションの最小ステップで固定して演算する領域を判断してくれます。
これにより、最小ステップで演算するロジックについては毎回演算を行い、それ以外は演算したシミュレーション値が許容誤差内である限りステップ数を伸ばして演算してくれるようです。
(このあたりまだ勉強中でして。。。違ってたらごめんなさい)
最小ステップ演算領域を可視化するには
こんな感じでSimulinkだと領域ごとの演算周期を色で示してくれます。
例えば最小ステップで固定されているのは灰色ですね。
ここのロジックが結構おもすぎると、毎回毎回重い演算をしてることになるので
前述したとおりシミュレーション全体の速度低下につながるかもしれません。
最小ステップ固定されている領域を最小限にして、演算を他の演算周期で実行させることが検討できるかと思います。
Simulinkは一つのモデルで離散と連続、そして異なるタイムステップで演算を実行することを許している。
— griffin921 (@griffin921) November 20, 2021
いったい何処でどんな周期で演算してるんだ?と知りたくなったときは「タイミング凡例」を表示すると便利。 pic.twitter.com/1vd3CgIbqG
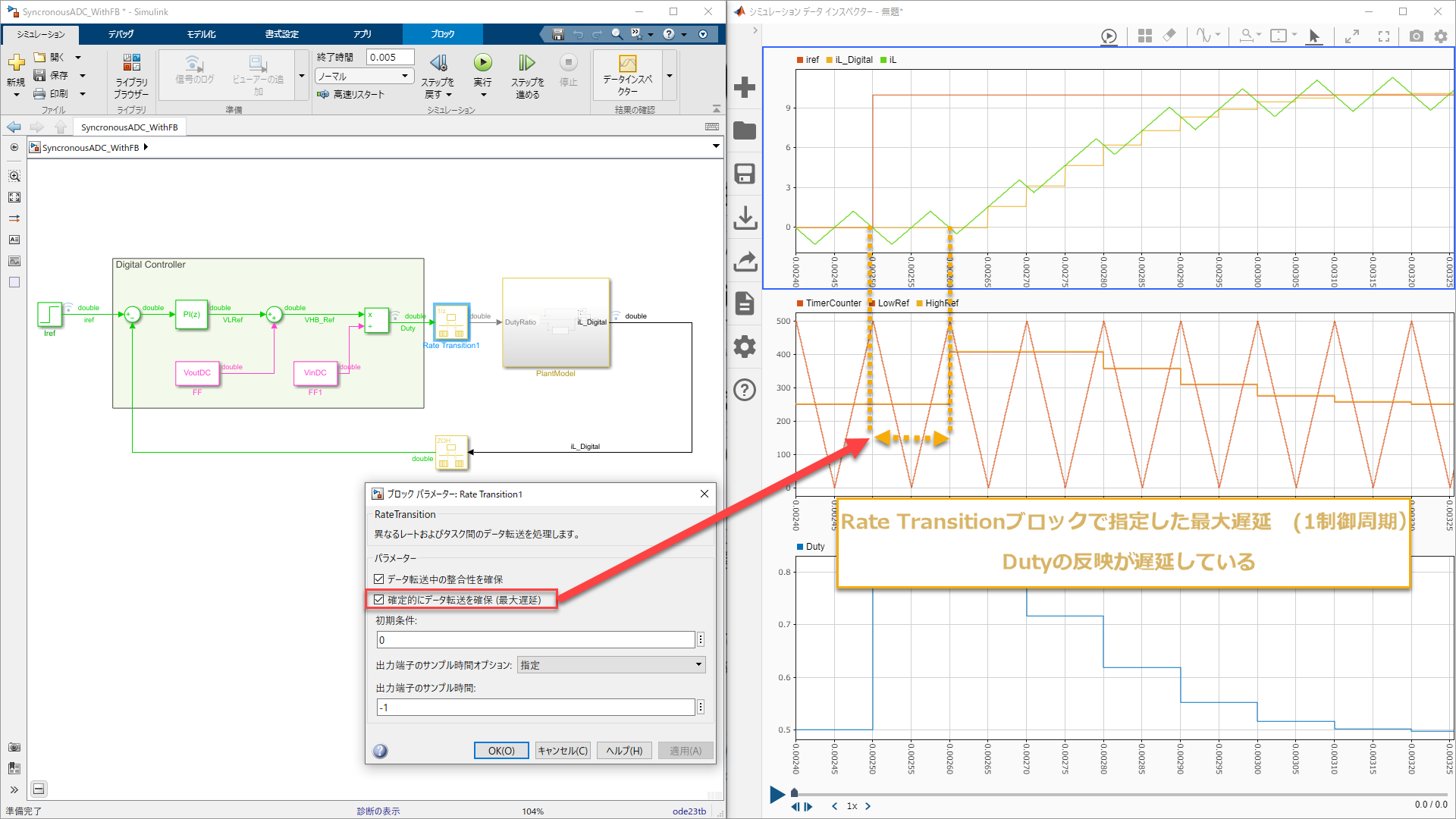
Duty反映のタイミング
前述しましたが、Simulinkでそのまま制御を書くと反映タイミングはRate Transitionブロックで指定したプロパティに応じてかわります。
これは異なる実行時間を持つロジックをつなぐときにその変換を行うブロックなのですが、
今回スイッチング周波数10kHzの逆数、100usがスイッチング周期なので
その100us周期ごとに緑の制御ロジック領域は演算されます。
Rate Transitionブロックで連続時間で実行しているPlantとつなげるのですが、
その際「確定的にデータ転送を確保(最大遅延)」とすると最大遅延で伝搬します。
制御遅れの最悪値でシミュレーションしたい場合には便利だと思います。
1周期内に演算が無事終わってDutyの反映もその次の周期までに間に合えば最悪でもこの応答より良い応答になるはずです。
(あくまでむだ時間おくれの影響についてですが)
あれ?怪文書?
真面目な記事になっちゃった!