Hello World!!
統計学と機械学習の初心者が、RとPythonを使って勉強しながらメモしていきます。
プログラミング経験は、非情報系が授業で習う程度のものなのでド素人にです。
少しずつ向上させることができたらなと思っています。
##ブートストラップ法
ブートストラップ法について昨日勉強したので記録します。
標本集合 $Z$ があったとします。この $Z$ から復元抽出によって新たな標本集合$Z'$を作ります。
この$Z'$のことを『ブートストラップ標本集合』と呼びます。
また、このサンプリングの仕方をブートストラップ法と呼びます。
※ブートストラップとは、ブーツのかかとの方にあるつまみのことをいうらしいです。
どうやら「人の手を借りない努力で自身をより良くする」の比喩に用いられていたことに由来するようで、たしかにこの方法も持っているデータだけでどうにかしようという気持ちが見受けられますね。
何回もデータを習得できる場合は、何回も取得して何回も分析をすればいいのですが、それは現実的ではないので、あたかも何回もサンプリングしたかのように演じる手法といったところでしょうか?
さて、今回はブートストラップ法を使って(単)回帰分析をしてみたいと思います。
訓練集合を
Z_{n}=\left\{ \left( X_{1},Y_{1}\right) ,\ldots ,\left( X_{n},Y_{n}\right) \right\}
とし、 $ Y $ を
$$ f(X) = \beta_{1} X + \beta_{0} $$
というモデルで予測します。
真のモデルは、
```math
Y = 5X + \varepsilon , \varepsilon \sim N\left( 0,4\right)
とします。それではやってみます。今回はブートストラップ標本を10個作ることにします。まずはデータのセットです。
n <- 50 #標本数
b <- 10 #ブートストラップ標本の数
x <- runif(n, -5, 5) # 一様乱数
e <- rnorm(n, 0, 4) # 正規乱数
y <- 5*x + e
X <- data.frame(y,x)
今のところこんな感じ。
X = \begin{pmatrix}y_{1}&x_{1} \\ \vdots&\vdots\\ y_{n}&x_{n} \end{pmatrix}
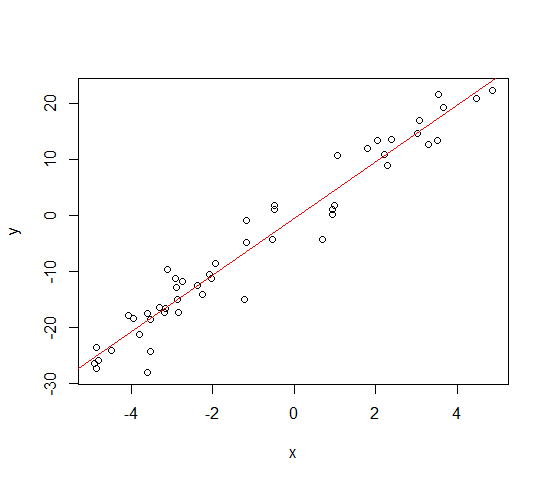
一応全データを使った回帰をしてみましょう。
ln.fit <- lm(y~x, data = X)
par(new=TRUE)
plot(y~x)
abline(ln.fit,col="red")
summary(ln.fit)
Call:
lm(formula = y ~ x, data = X)
Residuals:
Min 1Q Median 3Q Max
-9.2435 -1.9409 0.0188 2.0935 6.6884
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.5784 0.5217 -1.109 0.273
x 5.0584 0.1720 29.417 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.501 on 48 degrees of freedom
Multiple R-squared: 0.9474, Adjusted R-squared: 0.9464
F-statistic: 865.4 on 1 and 48 DF, p-value: < 2.2e-16
>
$$ \widehat {f}(X) = 5.0584X - 0.5784 $$
と推定されました。今回の目的は「やってみた」なので、係数の$p$値とかはとりあえず無視します。
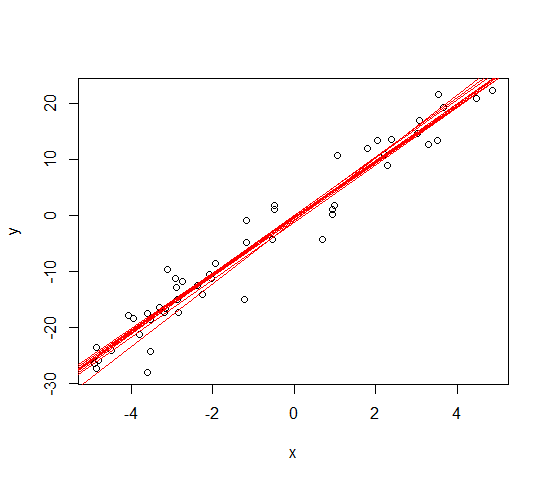
続いてブートストラップ法です。ついでに1つのブートストラップ標本集合で回帰するたびに直線も引いてみます。
#ブートストラップ
# i=1
X.boot <- as.list(NULL) #リストの初期化
X.num <- sample(nrow(X), n, replace = TRUE) #sample関数で行番号をn個無作為抽出
#replace=TRUEで復元抽出を指定
X.boot <- list(X[X.num,]) #Xから抽出した行番号と一致する行を習得
for(i in 1:(b-1)){
X.num <- sample(nrow(X), n, replace = TRUE)
boot <- data.frame((X[X.num,]))
X.boot <- c(X.boot, list(X[X.num,]))
ln.fit <- lm(boot[,1]~boot[,2]) #ついでに回帰
abline(ln.fit, col="red") #ついでに直線を引く
}
うん。なんかそれっぽいの引けてました。
見て勘づくかもしれませんが、ブートストラップは信頼区間を求めたりするのにも使います。
というか、たぶんそういう風に使うことが多いです。
ただし今回そこにふれることはしません。悪しからず。
また次のようにするとb番目のブートストラップ標本集合に同じものが何回出てきているのかを見ることができます。
一番左の列がもともとの訓練集合における行番号なのですが、小数点みたいになってますよね。
この.の右側の数字は、その行が出てきた何回目かという数字です。
> X.boot[[1]]
y x
33 -0.83984223 -1.1823657
16 -23.52309052 -4.8611497
2 -11.29088546 -2.0302543
20 1.04587906 0.9529472
13 0.07702314 0.9318630
27 -17.48683275 -3.5946244
34 22.35321343 4.8757321
15 -24.12908816 -4.4895790
24 20.85427234 4.4786934
19 -27.31266570 -4.8495618
5 10.84575482 2.2105942
9 -12.86358875 -2.8829739
43 -15.03068092 -2.8720738
24.1 20.85427234 4.4786934
44 -16.41073721 -3.3127177
43.1 -15.03068092 -2.8720738
9.1 -12.86358875 -2.8829739
37 -17.84476229 -4.0730172
22 10.73289090 1.0611087
30 -11.22250892 -2.9096548
39 -4.30507010 -0.5223382
47 -4.38378474 0.6969132
41 -9.57307625 -3.1003768
48 21.58668507 3.5533619
15.1 -24.12908816 -4.4895790
1 -25.89866352 -4.8047759
10 13.36028120 2.0369215
38 -17.25388111 -3.1790753
32 1.73803001 -0.4717056
26 -21.24393841 -3.8050913
2.1 -11.29088546 -2.0302543
4 12.61735252 3.2947134
9.2 -12.86358875 -2.8829739
50 -14.93808400 -1.2254289
40 8.98141702 2.2909006
27.1 -17.48683275 -3.5946244
3 -14.03387083 -2.2625380
14 -18.63006739 -3.5262929
6 11.99257330 1.8055589
37.1 -17.84476229 -4.0730172
21 -8.51777807 -1.9263721
45 13.41332843 3.5303534
20.1 1.04587906 0.9529472
22.1 10.73289090 1.0611087
2.2 -11.29088546 -2.0302543
23 -17.36916626 -2.8441248
35 -26.35043794 -4.8985021
41.1 -9.57307625 -3.1003768
8 -16.53691470 -3.1472653
28 -10.54761615 -2.0714463
ちなみに、あるブートストラップ標本集合に、ある標本が含まれない確率はおよそ37%です。なぜなら、
$N$個の標本から1回のランダム抽出で特定の1標本が選ばれない確率は、
\dfrac {N-1}{N}
であり、それを$N$回繰り返した時1回もその特定の標本が選ばれない確率は、
\left(\dfrac {N-1}{N}\right)^{N}
です。$N$について極限をとることにより、
\lim _{N\rightarrow ∞ }\left( \dfrac {N-1}{N}\right) ^{N}=\dfrac {1}{e}\fallingdotseq 0.37
したがって、だいたい37%ぐらいだということがわかりました。
※追記※
$ N→∞ $ の時の近似考えてもなぁ~と思ったので計算してみました。
# 関数作成
f = function(x){
((x-1)/x)^x
}
# N=1~15まで計算する
P = numeric(15)
for(i in 1:15){
P[i] = f(i)
}
P
[1] 0.0000000 0.2500000 0.2962963 0.3164062 0.3276800 0.3348980
[7] 0.3399167 0.3436089 0.3464394 0.3486784 0.3504939 0.3519956
[13] 0.3532585 0.3543353 0.3552644
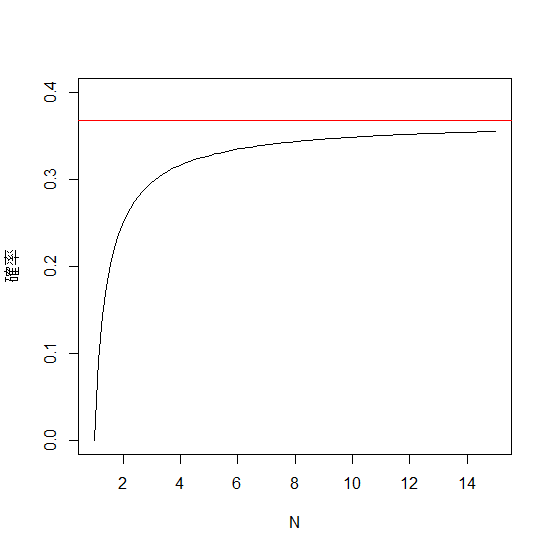
かなり収束が早いですね。グラフを描いてみましょうか。
> plot(f, 1, 15,ylim=c(0, 0.4), ylab="確率", xlab="N")
> abline(h=exp(-1),col="red")
これだけ早く収束するのであれば、∞としなくても近似として考えてもよさそうですね。
##★今回困ったこと★
データの型というものの違いがイマイチわからずに苦労しました。
そもそもプログラミング言語の基本について全く理解できていないということがわかったので、ぼちぼち勉強する必要がありますね。いい勉強になりました。
##★参考★
[1]Hastie,Tibshirani,Friedman:統計的学習の基礎(2009)