(2022-11-28 E問題の想定解を追記)
(2022-11-30 D問題の解析解アプローチを追記)
A - wwwvvvvvv
シグネチャを決める。
abc279a :: String -- S
-> Int -- 答え
vなら1、wなら2を数えて、足し合わせればよい。
結果
abc279a = sum . map f
f 'v' = 1
f 'w' = 2
B - LOOKUP
シグネチャを決める。
abc279b :: String -- S
-> String -- T
-> Bool -- 答え
そのものズバリのライブラリ関数がある。
結果
import Data.List
abc279b = flip isInfixOf
C - RANDOM
シグネチャを決める。
abc279c :: Int -- H
-> Int -- W
-> [String] -- Si
-> [String] -- Ti
-> Bool -- 答え
縦の列で考えて、SとTが一対一対応するかどうかが知りたい。
結果
手っ取り早くするには、整列して等しいか判定すればできる。
import Data.List
abc279c :: Int -> Int -> [String] -> [String] -> Bool
abc279c h w ss ts = sort (transpose ss) == sort (transpose ts)
すごい手抜きだけど、問題サイズがそれほどでもないので間に合った。
別解
丁寧にするなら、先頭から順に、文字が . のものと # のものに分けて、
その個数が同じであることを確認することを、空リストになるまで再帰的に繰り返せばよい。
import Data.List
import Data.Array
abc279c :: Int -> Int -> [String] -> [String] -> Bool
abc279c h w ss ts = recur (transpose ss) (transpose ts)
recur ss ts
| length ss /= length ts = False
| null ss = True
| null (head ss) = True
| otherwise = recur ss1 ts1 && recur ss2 ts2
where
(ss1,ss2) = sub ss
(ts1,ts2) = sub ts
sub css = ([cs | '.':cs <- css], [cs | '#':cs <- css])
これは結局、 [Bool] をバケツソートして、全体が等しいか確認しているのにほぼ同じ。途中で食い違いが起きたときにその段階で止まれる分これの方が速いといえる。
D - Freefall
シグネチャを決める。
abc279d :: Int -- A
-> Int -- B
-> Double -- 答え
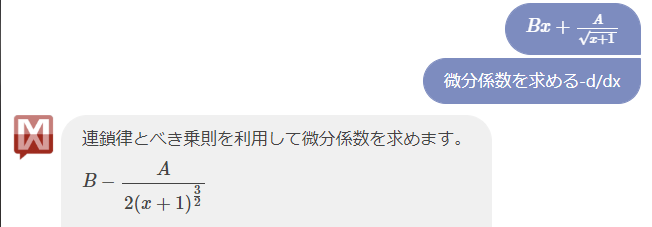
超能力を $k$ 回使うと時間を $kB$ 秒消費し、その後加速度 $1 + k$ で落下するのに $\frac{A}{\sqrt{k + 1}}$ 秒かかる。
地面に到達する時刻を $k$ の関数にすると $f(k) = kB + \frac{A}{\sqrt{k+1}}$ となる。
グーグル先生に x + 1/sqrt(x + 1) と尋ねると
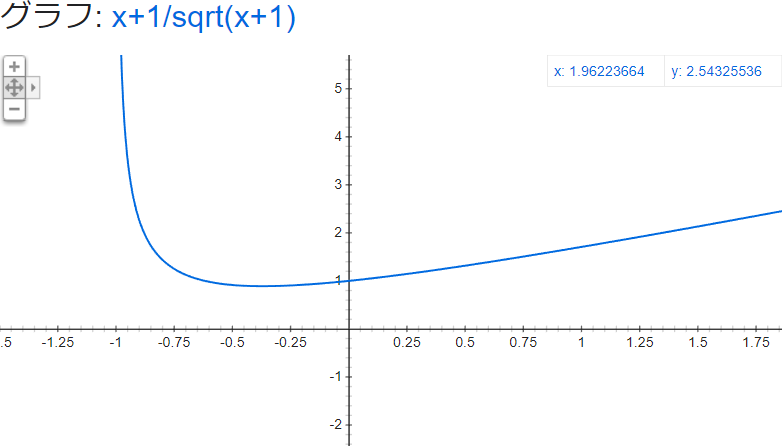
と概形を見せてくれて、下に凸な感じになるのだろうとわかる。
数学が得意ならここから$f(x)$を微分して、$f'(x_1) = 0$ となる $x_1$ を求めて、$\min(f(\lfloor x_1 \rfloor),f(\lceil x_1 \rceil))$ を計算したらよいと思うが、いまいちうまくできなかった(追記あり)ので、二分探索で求める。
超能力を一度も使わなかったとき $f(0) = A$ となり、超能力を $A$ 回使ったとき $f(A) > A$ となることは自明にわかる。よって、二分探索の探索範囲は 0 から A ととればよい。
(もうすこし考えると、$f(\frac{A}{B}) = A + \frac{A}{\sqrt{\frac{A}{B} + 1}} > A$ なので上限は $\lceil A/B \rceil$ でよかったようだ。)
探索の条件は $f(k) \leq f(k+1)$ つまり「そこから先はもう値が下がらない」ことである。
二分探索が健全に機能するために、位置0でこの条件が成り立たないことを保証しておく必要がある。
結果
abc279d :: Int -> Int -> Double
abc279d a b
| prop 0 = f 0
| otherwise = f k
where
ra = fromIntegral a
rb = fromIntegral b
f k = x * rb + ra / sqrt(x + 1) where x = fromIntegral k
prop k = f k <= f (succ k)
(_, k) = binarySearch prop (-1) a
-- @gotoki_no_joe
binarySearch :: (Int -> Bool) -> Int -> Int -> (Int, Int)
binarySearch prop unsat sat = until goal step (unsat, sat)
where
goal (ng, ok) = abs (ok - ng) <= 1
step (ng, ok) = if prop mid then (ng, mid) else (mid, ok)
where
mid = div (ok + ng) 2
追記:解析解
(2022-11-30 追記) 解析解を求めるアプローチ。
x + 1/sqrt(x+1) でググるとグラフが表示されるとともに、Mathematica的なサイトがいくつか表示される。そのうちの一つ Mathway を使ってみる。
Mathwayさんは sqrt が通じないのでソフトキーから√記号を入れて、数式を入れると何をするか聞いてくれるから、$x$ について微分してもらう。
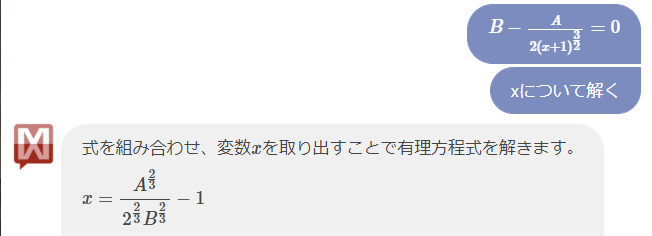
さらにこれが0になるような $x$ の値も求めてもらう。
$x = (\frac{A}{2B})^{\frac{2}{3}} - 1$
超能力を使う回数は自然数なので、これを直接与えるのではなくて整数化すること、切り捨てと切り上げの両側で小さい方を選ぶようにすること、$x < 0$ となるときに気を付けること、$A,B$は最初から浮動小数点数で考えてしまっていいことから、コードはこうなる。
abc279d :: Double -> Double -> Double
abc279d a b
| x < 0 = f 0
| otherwise = min (f $ floor x) (f $ ceiling x)
where
x = (a / (2 * b)) ** (2/3) - 1
f k = x * b + a / sqrt(x + 1) where x = fromIntegral k
サンプル3の結果が見た目が違ってびっくりするけれど、
8.772053214538598e12 : 出力 (科学記数法)
8772053214538.5976562500 : 正解
8772053214538.598 : 出力の小数点位置を直したもの
と、ちゃんと正解が出ている。
E - Cheating Amidakuji
シグネチャを決める。
abc279e :: Int -- N
-> Int -- M
-> [Int] -- Ai
-> [Int] -- 答え
ようは($B_2$から$B_N$は関係なくて)$B_1$があみだくじで何番の線に到着するのか、ただし横の線をどれか1本除いたときのバリエーションを全て求めよ、という問題。
バリエーション$1$から$M$について、どれも最初は線1にいる。
横線 $A_i$ に遭遇したとき、$A_i$ にいるバリエーションと $A_i + 1$ にいるバリエーションの位置を交換する。ただしその中で、バリエーション $i$ は交換せず同じ線に留まる、という計算を$1$から$M$まで進める。
すると、それぞれの線$1$から$N$に到着したバリエーションは誰か、という向きの情報が得られる。これを「バリエーション$j$は何番の線に到着したか」という逆引きに戻したものが答え。
実装
考え方はこれでよいが、状態の表現、すなわち実装を注意深く選択する必要がある。
MVector [Int]
頻繁な交換が発生する「線に属するバリエーション」を MVector にするのは理にかなっている。
(ただし命令的でHaskell的でないコードになる)
それで性能は十分得られるとタカをくくって、「バリエーションの集まり」を [Int] で表したところ、見事にTLEした。
「集まりの中の $i$ はその場にとどまる」を elem, filter などでナイーブに表現してはいけない。
MVector (MVector Bool)
バリエーション $i$ がその線に居ることを表すフラグ集合で表現すれば $O(1)$ でアクセスできて、交換にかかる時間を最小にできる。
単純な2次元配列では、線の交換に $O(N)$ かかってしまうが、2段階の配列ならポインタの入れ替えだけなのでそこも問題ない。
しかし結果はTLEだった。
ゴールまで到達した後で、逆引き表を作るために、$MN$ 要素を参照する方の計算量が支配的になってしまうようだ。
MVector IntSet
Data.Set は $O(\log N)$ かかるが Data.IntSet は $O(1)$ 動作なので、実は優秀。(定数は大きいが)
この組み合わせでACした。タイムは311ms。
IntMap IntSet
同様に、Data.Map は $O(\log N)$ なのに対して Data.IntMap は $O(1)$ 動作をするので、これを使って純粋に実装しよう。
結果
import qualified Data.IntSet as IS
import qualified Data.IntMap as IM
import Data.Array
abc279e :: Int -> Int -> [Int] -> [Int]
abc279e n m as = elems aa
where
-- 全てのバリエーションが1に集まっている
bs1 = IS.fromAscList [1..m]
lines0 = IM.fromAscList $ zip [1..] $ bs1 : replicate (pred n) IS.empty
-- Aiを使ったり使わなかったりして最下段まで降りる
linesN = foldl' {-'-} step lines0 $ zip [1..] as
-- バリエーションのいる位置の逆引き表を作る
aa = array (1,m) [(b, si) | (si, bs) <- IM.assocs linesN, b <- IS.elems bs]
-- i段めのAiとAi+1を入れ替える、ただしiは残留
step lines (i,ai)
| IS.member i lai = sub (IS.delete i) (IS.insert i) -- aiにいるiを残留させる
| IS.member i lai1 = sub (IS.insert i) (IS.delete i) -- ai1にいるiを残留させる
| otherwise = sub id id -- どちらにもiはいない
where
ai1 = succ ai
lai = lines IM.! ai
lai1 = lines IM.! ai1
-- ai1にfi lai, aiにf0 lai1を入れる(入れる前に加工を施せる)
sub f1 f0 = IM.insert ai1 (f1 lai) $ IM.insert ai (f0 lai1) lines
854msでACした。
命令的なMVector版よりずっとコンパクトなコードにできた。
この実装を下敷きにしたMVector版の方が、上のMVector IntSetのものよりはMVector化の参考になるだろうか。
追記:想定解
(2022-11-28 追記)
速報解説
https://twitter.com/kyopro_friends/status/1596501785682006016
で示された解法。
縦線1から出発して、横線$A_1, A_2, \dots$ を辿って降りて行ったときの縦線の位置をそれぞれ把握しておく。
forwards = scanl fstep 1 as
fstep x a
| x == a = succ a
| x == succ a = a
| otherwise = x
ゴールの縦線$1$~$N$が、横線$A_M,A_{M-1},\dots$とさかのぼったとき、それぞれどこに来るのかをそれぞれ考える。
backwards = scanr bstep mM as
mM = IM.fromAscList [(i,i) | i <- [1..n]]
bstep a im = IM.insert a (im IM.! succ a) $ IM.insert (succ a) (im IM.! a) im
横線をひとつ飛ばすように、forwardsで$A_{i-1}$まで辿ったときの1の位置から、backwardsで$A_{i+1}$以降を辿ったときに縦線の何番にたどり着くかをひくと$B_j$の$j$が得られる。
abc279e n m as = zipWith (IM.!) (tail backwards) forwards
where
...
このまま実行して1076 ms。backwardsの更新の遅さと、結果を前方から確定させていくと、それまでのbackwardsの内容がメモリに全て展開されることがネックなので、後ろから計算して不要な対応は捨てるようにし、IntMapでなくMVectorを使うように改善すると166msまで高速化した。reverseを使わないようにベクタにasやforwardsを格納してインデックスで後ろから利用すればもっと高速化できると思うが、ここまでにしておく。
F - BOX
シグネチャを決める。
abc279f :: Int -- N
-> Int -- Q
-> [[Int]] -- op_i
-> [Int] -- 答え
箱に入っているボールをひとつにまとめる操作はあるが、それを分割する操作はないので、UnionFindが使えそう。ただしそれだけでは、その分割がどの箱に入っているのか、という情報がない。結局、「分割の代表ボール $R \to$ その分割が入っている箱の番号 $X$」という部分写像と、その逆写像「箱の番号 $X \to$ その箱に入っている分割の代表ボール $R$ ただし箱が空のときは $0$ (*)」という両向きの対応を同時に維持する必要がある。
(*) 原理主義者なら「箱が空のとき Nothing な Maybe Int」とするところだが、さすがにメモリと時間の無駄。
UnionFindの実装が配列ベースで、要素数を最初に固定する場合、タイプ2の操作で要素が追加される分を見越して、1から$N+Q$までの要素を持つUnionFindを作る必要がある。
結果
UnionFindと二つの写像の全てを IntMap で実装して、純粋な計算で(ただし、操作ごとに読み込んでは実行し、タイプ3では出力を行うためにIOアクションになっている)実現した版で、1742msで間に合った。
UnionFindは経路圧縮も、サイズに基づく簡略化した動作しか行っていない。
時間制限のある中で、両方向きの写像を丁寧に維持するコードを書くというのはつらそうだ。