ABC295は全然わからなくて宿題になっています。
それと比べると今回はよく解けた。
A - Alternately
シグネチャを決める。$N$ は不要。
abc296a :: String -- S
-> Bool -- 答え
隣り合う要素が全て異なっていればよい。
結果
abc296a s = and $ zipWith (/=) s (tail s)
B - Chessboard
シグネチャを決める。
abc296b :: [String] -- Si
-> String -- 答え
列の中に '*' は1つだけなので、そうである場合の添え字を取りだせばよい。
結果
abc296b css = head
[ [j,i]
| (i, cs) <- zip ['8','7'..] css
, (j, '*') <- zip ['a'..] cs
]
C - Gap Existence
シグネチャを決める。
abc296c :: Int -- N
-> Int -- X
-> [Int] -- Ai
-> Bool -- 答え
$A_i$を全て集合に放り込んでおき、
$A_i + X$ がその中に含まれるか一つずつ調べればよい。
結果
import qualified Data.IntSet as IS
abc296c :: Int -> Int -> [Int] -> Bool
abc296c n x as = any prop as
where
s = IS.fromList as
prop a = IS.member (a + x) s
マニュアルを信じるなら、この方法の計算量は、集合の構築が $O(N)$、検索一回が $O(1)$ で $O(N)$ となる。
別解
$A_i$ をソートしておき、左端$+X$ 以上の要素を右端とする尺取り法で列を一度舐めて、ちょうど$+X$な幅がとれたら成功、という尺取り法でもできそう。
この方法の計算量は、ソートが $O(N \log N)$、尺取り法が $O(N)$ で、$O(N \log N)$ となる。
D - M<=ab
シグネチャを決める。
abc296d :: Int -- N
-> Int -- M
-> Int -- 答え
$N \times N$ の巨大な九九の表を考える。
$a$ の段ごとに、$M$以上の最小値は一ヵ所に決まる。それは具体的には切り上げ除算の結果 $b = \lceil N/a \rceil$ により $ab$ と求められる。この値は九九の表の中で $y = M/x$ のグラフに対応する双曲線上に位置する。
そのような $(a,b)$ のうち、$N < b$ なものは除外する。これは$a$が小さい範囲で現れうる。
また、$a \leq b$ のものだけ考えればよい。対角線に関して対称なので、ここで止めればよい。
これは $\sqrt M \leq 10^6$ となり、線形探索できるサイズである。
結果
候補 $ab$ の最小値を返すが、候補が一つもない可能性がある。
abc296d n m
| null cands = -1
| otherwise = minimum cands
where
cands =
map (uncurry (*)) $
takeWhile (uncurry (<=)) $
[(a, b) | a <- [1..], let b = divrup m a, b <= n]
divrup x y = negate $ div (negate x) y -- 切り上げ除算
twitterのトレンドに sqrt が上がっていて、何かと思ったらこの問題の話で、探索の上限を sqrt(m)と、整数の問題なのに実数の関数を使うことの是非、整数の範囲でするために二分探索を持ち出すことの効率、云々だった。
しかしその辺をごちゃごちゃすると、境界が怪しくなるせいか、どうもACしないのでこれで止めておく。
E - Transition Game
シグネチャを決める。
abc296e :: Int -- N
-> [Int] -- Ai
-> Int -- 答え
1から$N$を頂点として、$x$ から $A_x$ に有向辺が生えたグラフをなしている。
各頂点から出る辺は1本しかないので分岐はない。ただし合流やループはある。
全ての頂点に出る辺があるので、行き止まりもない。
$i$回めのゲームに高橋君が勝つには、コールされた $K_i$ ステップで $i$ に到達する出発点を選ぶ。
青木君はそれを避けるために、頂点 $i$ にそのステップ数ではちょうど到達できないような $K_i$ をコールすればよいが、そのような数が $i$ に存在しない、つまりいくつとコールしてもそのステップ数で $i$ に至ることができるようなグラフなら、またそういう場合にのみ負ける。(高橋君が勝つ。)
一般のグラフにおいて、そういうノードであるかどうかは強連結成分であるかどうか、になる。
https://hkawabata.github.io/technical-note/note/Algorithm/graph/scc.html
(上のtweetにSCCというキーワードも入っていて、解く前にヒントを見てしまった。)
ただし、この問題のグラフは枝分かれがないので、同じ方針のもっと単純な計算でSCCを取り出せる。
深さ優先探索は分岐することなく一直線に降りていき、最終的には訪問済み(今回またはそれ以前の探索で)の頂点に到達して終わる。
今回の探索中に訪問したノードに突き当たったならば、そこから先の最終地点までがループをなす。それ以外はループしていない。
以前の探索で訪問済みのノードに突き当たったならば、今回探索したノードは全てループをなさない。
この、ループの中のノードは高橋君の勝つノードなので、その個数を数える。
結果
STArrayで頂点の訪問済みフラグを管理する。
import Data.Array
import Data.Array.ST
import Control.Monad.ST
abc296e :: Int -> [Int] -> Int
abc296e n as = runST $
do
-- 訪問済みフラグ配列 出発点 i の探索で訪問したことを意味する。0 は未訪問
ma <- newArray (1,n) 0 :: ST s (STUArray s Int Int)
sum <$> forM [1..n] (\i -> step1 ma i i)
where
aa = listArray (1,n) as
-- 訪問済みの頂点まで降りる。出発点i現在位置j
step1 ma i j = do
x <- readArray ma j
if x == 0 then writeArray ma j i >> step1 ma i (aa ! j) else
return (if x == i then step2 j 1 (aa ! j) else 0)
-- ループのノード数を数える。ゴールj現在位置k
step2 j cnt k
| j == k = cnt
| otherwise = step2 j (succ cnt) (aa ! k)
別解(ダブリング)
それ以上回しても循環するだけなので、ステップの最大値はNであること、また、全ての開始位置から十分進めたとき、全てのコマがループに囚われること、はわかる。
十分進めたとき、コマがダマになって、たまたま無人になるマスがないこと、は即座に自明でもない。初めからループの中に居たコマがグルグル回っているから、で説明がつくけれど。
なので、十分なステップ数だけ状況を進めて、重なりを無視してコマのあるマスの個数を数えたら、それがループに含まれる頂点の個数になる、とすれば答えが求まる、という解説 ダブリングを使った実装方法 by shakayamiをやってみる。
import Data.Array.Unboxed
abc296e :: Int -> [Int] -> Int
abc296e n as = sum $ elems cA
where
a0 = listArray (1,n) as :: UArray Int Int
aD = fst $ until ((0 ==) . snd) step (a0, n)
step (a, k) = (listArray (1,n) $ map (a !) $ elems a, div k 2)
cA = accumArray (flip const) 0 (1,n) [(a, 1) | a <- elems aD] :: UArray Int Int
30回決め打ちだと回しすぎでもったいないので、Nを2で割り続けて0になったら終わり、としている。
map (a !) $ elems a は fmap (a !) a で書けるかと思ったら怒られる理由がわからない。
Pythonだと A=[A[a] for a in A] で書けるという、なんというかすごい構文だ。
F - Simultaneous Swap
問題Eと同様に、転倒数というキーワードはtwitterで見えてしまったのだけど、それでもわからなかったので、より高速な解法 by MMNMM を写経する。
シグネチャを決める。
abc296f :: Int -- N
-> [Int] -- Ai
-> [Int] -- Bi
-> Bool -- 答え
abc296f n as bs = ...
考える
条件1
まず、例2のように、$A_i$ と $B_i$ の内容が同一でないと始まらない。
ソートして比較
cond1 = sort as == sort bs
だと $O(N \log N)$ 、カウントして比較
cA = accumArray (+) 0 (1,n) [(a,1) | a <- as]
cB = accumArray (+) 0 (1,n) [(b,1) | b <- bs]
cond1 = cA == cB
だと $O(N)$、またカウント値は次でも使えるので、こちらにする。
条件2
値に重複があるならば、同じ値どうしで交換すれば、片方だけを好きなだけ交換できるので、それ以上条件なしに常に目標を達成できる。上で作ったカウント値に2以上の値があればよいし、逆に0があっても、その分他に入っているはずで、結局、1でない値が見つかればよい。
cond2 = any (1 /=) $ elems cA
条件3
条件2が満たされない場合、真面目に$A_i$と$B_i$を同時に交換する操作を繰り返して、同じ並びにする必要がある。
両者を何らかの最終形に並び替えるために必要な操作回数がそれぞれ$p,q$回だったとする。
$p == q$ なら問題ない。そうでないとき、その差が偶数なら、少ない方は $x \leftrightarrow y$, $y \leftrightarrow x$ と無駄な交換をして辻褄を合わせることができる。
結局、$p$と$q$の偶奇が同じならよい。
とここで、「$A[i]$ と $B[i]$ の置換の偶奇は等しい」と「$P[i] = B[A[i]]$ が偶置換」が同値なのだそうで、$P_i$を整列するのにかかった置換の回数が偶数になるかを数える。
解説では、$P[i] \neq i$なときに、$i$が入っている位置$j$ ($P[j]=i$) を $P$ の逆写像 $P^{-1}$ で取り出して ($P^{-1}[i] = j$)、確実に $P[i] = i$ を達成する方針でやっている。
このときループは必ず1からNを一度ずつ、置換は最大N回で完了する。
逆写像も同時に維持するのが面倒なので、$P[i] = j \neq i$なときに、$P[i]$と$P[j]$を交換する、つまり$j$を$P[j]$に戻し、追い出された$P[j] = k$を$P[i]$に入れる。こうすると$P[j]=j$となり、一ヵ所は正しくなる。$k \neq i$だと$P[i] \neq i$のままなので、これが一致するまで次には進めない。
こうすると「1からNを一度ずつ」というループではなくなるが、置換は最大N回で完了するので、計算量はある意味変化しない。
配列をごりごり更新するのでSTArrayを用いる。
ba = listArray (1,n) bs
cond3 = runST $ do
p <- newListArray (1,n) $ map (ba !) as
loop p 1 True
loop :: STUArray s Int Int -> Int -> Bool -> ST s Bool
loop p i ans
| n < i = return ans
| otherwise =
do
j <- readArray p i
if i == j then loop p (succ i) ans
else swap p i j >> loop p i (not ans)
-- p[i]=jなとき専用、p[i]とp[j]を交換
swap p i j = do
x <- readArray p j
writeArray p i x
writeArray p j j
答え
abc296f n as bs = cond1 && (cond2 || cond3)
転倒数がらみは苦手…
G - Polygon and Points
反時計回りとわかっているので、$Y_k < Y_{k+1}$ ならば上昇しているので右側、逆なら下降する左側とわかる。
右側と左側と別々に、頂点のY成分をキー、X成分を値として IntMap に入れておけば、
$(A_i, B_i)$ に対して、これが内側にあるかどうか判定できる。
ということで、この二つの IntMap (と、$Y$成分の有効範囲)を作る前処理と、クエリに応答する部分で分割する。
import qualified Data.IntMap as IM
type DAT =
( Int, Int -- Y下限, 上限
, IM.IntMap Int -- 左側のmap
, IM.IntMap Int) -- 右側のmap
-- 答えのための列挙型
type ANS = OFF | ON | IN deriving Show
-- 前処理
abc296gp :: Int -- N
-> [(Int,Int)] -- Xi, Yi
-> DAT -- 前処理結果
-- クエリ対応
abc296gm :: DAT -- 前処理情報
-> Int -- Ai
-> Int -- Bi
-> ANS -- 答え
結果
$B_i$ と同じ高さに頂点があるとき、そのX座標と$A_i$を比較すればよい。
上下にずれた二つの点 $(X,Y), (Z,W)$ があったとき $(Y < B_i < W)$、この2点を結ぶ線が$Y=B_i$と交わる点のX座標は、
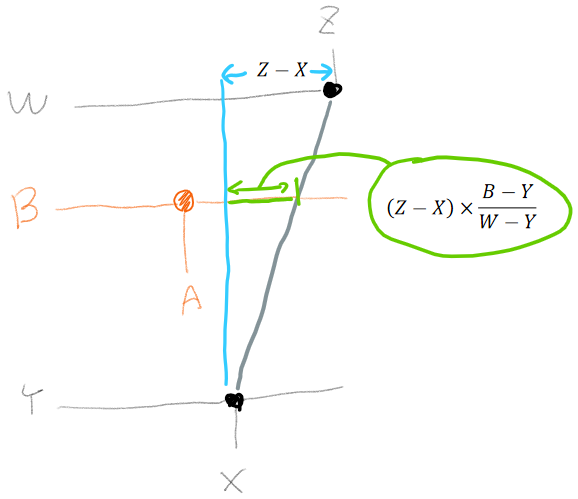
$X + (Z-X) \times \frac{B-Y}{W-Y}$ となる。これと $A_i$ を比較する。式変形すると
$(Z-X)(B-Y)$ と $(A_i - X)(W-Y)$ を比較すればよいとわかる。
-- 前処理
abc296gp :: Int -> [(Int,Int)] -> DAT
abc296gp n xys = (fst $ IM.findMin rm, fst $ IM.findMax rm, lm, rm)
where
rm = mkMap (<)
lm = mkMap (>)
mkMap rel = IM.fromList
[ p
| ((x1,y1),(x2,y2)) <- zip (last xys : xys) xys
, y1 `rel` y2
, p <- [(y1,x1),(y2,x2)]
]
-- クエリ対応
abc296gm :: DAT -> Int -> Int -> ANS
abc296gm (lb, ub, lm, rm) a b
| b < lb || ub < b = OUT
| otherwise =
case (check1 lm a b, check1 rm a b) of
(EQ, _ ) -> ON
(_ , EQ) -> ON
(LT, GT) -> if b == lb || b == ub then ON else IN
_ -> OUT
check1 :: IM.IntMap Int -> Int -> Int -> Ordering
check1 im a b
| b == y = compare x a
| otherwise = compare ((z-x)*(b-y)) ((a-x)*(w-y))
where
Just (y, x) = IM.lookupLE b im
Just (w, z) = IM.lookupGT b im
水平に走る辺についてはIntMapに記録されていない。$(A_i, B_i)$ が左右にはさまれて IN のように見えるが、$B_i$ が下限または上限ちょうどのとき、実際には水平の辺に乗っていて ON と答える必要がある。
普通の幾何的な解(TLE)
反時計周りなので、隣接する2点を$P, Q$、クエリの点を $X$ とするとき、外積 $\vec{PQ} \times \vec{PX}$ を全て計算し、一つでも負があるときOUT、一つでも0があるときON、全て正のときIN、としたくなるが、それをすると $O(NQ)$ になって間に合わない。