Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@gotoki_no_joe(じょお)

ABC270 A～F をHaskellで

Last updated at Posted at 2022-09-24

A - 1-2-4 Test

問題 ABC270A

シグネチャを決める。

abc270a :: Int   -- A
        -> Int   -- B
        -> Int   -- 答え

配点は $2^0, 2^1, 2^2$ になっているので、高橋君、青木君が解けた問題とは2進数でビットが1になっている問題である。すぬけ君はどちらかが解けた問題だけが解けたのだから、その論理和をとればよい。

結果

import Data.Bits

abc270a :: Int -> Int -> Int
abc270a = (.|.)

B - Hammer

問題 ABC270B

シグネチャを決める。

abc270b :: Int   -- X
        -> Int   -- Y
        -> Int   -- Z
        -> Int   -- 答え

負の数もありうるので、場合分けが少々面倒くさい。

  • 原点からゴールまでの間に壁がないなら、まっすぐ向かえばよい。
  • そうでないとき、壁を壊す必要がある。そこで
  • 原点から壁の間にハンマーがあるなら、結局、まっすぐ進めばよい。
  • そうでないとき、ハンマーは壁の向こうであるか、壁と反対側にあるかのどちらかである。
  • 反対側にある場合は、ハンマーを取りに行き、戻ってきて、壁を越えてゴールに行く。
  • 同じ側にあるときは、ハンマーが入手できずゴールには到達できない。

この「原点とPの間にQがある」を、正負を気にせず判定できるように括りだすと見通しがよくなる。

結果

abc270b x y z
  | not (isIn y x) = abs x
  | isIn z y = abs x
  | signum y /= signum z = 2 * abs z + abs x
  | otherwise = -1

isIn q p
  | 0 < q = q < p
  | True  = p < q

C - Simple path

問題 ABC270C

シグネチャを決める。

abc270c :: Int           -- N
        -> Int -> Int    -- X,Y
        -> [(Int,Int)]   -- Ui,Vi
        -> [Int]         -- 答え

いつものように、グラフを、頂点から（隣接する頂点のリスト）への配列で表し、$Y$ から深さ優先探索で $X$ まで到達する経路を再帰的に作る。逆順にするのはHaskellのリストは前に付け足すべきだから。

結果

loopにおいて、探索が親に戻らないように、現在のノード c だけでなく親ノードの番号 p も渡す。初期値には存在しないノード番号である0を渡す。
深さ優先探索で $X$ に到達できなかったときは失敗して別の分岐を試すために、結果を Maybe で包んでいる。分岐のいずれか一つ成功したものを取り出す動作を（Maybeモナドの） Control.Monad.msum で作っている。

import Control.Monad
import Data.Array

abc270c :: Int -> Int -> Int -> [(Int,Int)] -> [Int]
abc270c n x y uvs = ans
  where
    g = accumArray (flip (:)) [] (1,n) [p | (u,v) <- uvs, p <- [(u,v),(v,u)]]
    Just ans = loop [] 0 y
    loop vs p c
      | c == x = Just (x:vs)
      | null vs = Nothing
      | otherwise = msum $ map (loop (c:vs) c) $ filter (p /=) $ g ! c

D - Stones

問題 ABC270D

シグネチャを決める。

abc270d :: Int     -- N
        -> Int     -- K
        -> [Int]   -- Ai
        -> Int    -- 答え

単純に、山からとれるだけたくさん取る、という貪欲法でWAしてしまった。つまり、あえてそれより少ない数をとることで、相手を妨害できる場合があるということ。どんな場合なのかはよくわからないけれど。

誤答

とりあえず間違った貪欲な方法から。
現在とれる最大手を効率的に見つけるとは、今の山の石数 $m$ 以下の $A_i$ を見つけるということ。それは、二分探索というか、Data.IntSet.lookupLE で実現できる。
$N \leq 10^4$と大したことないので、互いの手を実際に追う方法でも時間は足りる。

import qualified Data.IntSet as IS

abc270d :: Int -> Int -> [Int] -> Int
abc270d n k as = sum $ loop n True
  where
    aS = IS.fromAscList as
    loop m myTurn =
      case IS.lookupLE m aS of
        [] -> []
        Just ai -> if myTurn then ai else 0 : loop (m - ai) (not myTurn)

正答

山の石数 $m$ に対して、ここから始めたときの自分の最大スコアと、そのときの相手の最大スコア、の対を動的計画法で表 $s[m]$ にする。
つまり、全ての $A_i \leq m$ について、自分が $A_i$ を着手したとき、続けて相手は $s[m - A_i] = (S, T)$ になるから、結果は $(T + A_i, S)$ となる。その中で左が最大になるやり方を選べばよい。
$m < A_1$ で手がないときは $(0,0)$ とする。

import Data.Array

abc270d :: Int -> Int -> [Int] -> Int
abc270d n k as = fst $ arr ! n
  where
    arr = listArray (0,n) $ map f [0..n]
    f m = maximum $ (0,0) :
          [ (t + a, s)
          | a <- takeWhile (m >=) as
          , let (s, t) = arr ! (m - a)
          ]

E - Apple Baskets on Circle

問題 ABC270E

シグネチャを決める。

abc270e :: Int     -- N
        -> Int     -- K
        -> [Int]   -- Ai
        -> [Int]   -- 答え

カゴの個数が多いので、いくつかリンゴを減らしたとき、全てのカゴからその個数を引く、ということをやりだすと時間が足らなくなるので、そういう操作をしないで済むように工夫する必要がある。

今、リンゴがあと $X$ 個必要であるとする。

空になったカゴは無視して、まだリンゴが入っているカゴが $V$ 個あるとして、それらの最小のリンゴの個数が $K$ のとき、一周回るとリンゴが $V$ 個手に入ることを $K$ 周することができる。これで全てのカゴから $K$ 個のリンゴが減り、あと必要なリンゴは $X - KV$ 個になる。

そして、元々リンゴが $K$ 個だったカゴがこれで空になり、残りのカゴで続きをする。

$X \leq KV$ のときは、周回の途中で $X$ 個に足りる瞬間が訪れる。それは、$(q,r) = \textrm{divMod}(X,V)$ として $q$ 周回った次の周回の $r$ 個めの（空でない）カゴまで、となる。
このときに、トータルで何周したか（つまり全てのカゴから何個ずつリンゴを取ったか）と、最後の周で何個めの空でないカゴまで追加でリンゴを取ったか、が判明する。

最終的に返すべき、事後の全てのカゴのそれぞれのリンゴの個数は、まずそれらから周回数を引く。ただし0で打ち止めにする。そして、0でないもの前から$r$個をさらに1減らす。という手順で求められる。

各段階で必要な$K,V$の値は、リンゴが$A$個以上入っているカゴの個数$C$という単調減少するグラフをかいたとき、
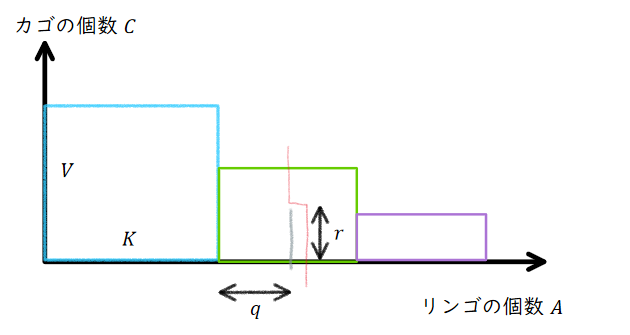
image.png
このそれぞれの長方形の幅が$K$、高さが$V$である。
これはリンゴの個数に対するカゴの数のヒストグラムから、カゴの数は累積和をとり、リンゴの個数は一つ手前との差分をとることで作れる。

結果

import qualified Data.IntMap as IM

abc270e :: Int -> Int -> [Int] -> [Int]
abc270e n x as = post r $ map (max 0 . subtract q) as
  where
    (ks0,vs0) = unzip $ IM.assocs $ IM.fromListWith (+) [(a, 1) | a <- as]
    ks = zipWith (-) ks0 (0 : ks0)
    vs = scanr1 (+) vs0
    (q, r) = loop 0 x ks vs
    loop acc x (k:ks) (v:vs)
      | x > k * v = loop (acc + k) (x - k * v) ks vs
      | otherwise = let (q, r) = divMod x v in (acc + q, r)
    post 0 xs = xs
    post r (0:xs) = 0      : post       r  xs
    post r (x:xs) = pred x : post (pred r) xs

F - Transportation

問題 ABC270F

シグネチャを決める。

abc270f :: Int -> Int        -- N,M
        -> [Int]             -- Xi
        -> [Int]             -- Yi
        -> [(Int,Int,Int)]   -- Ai,Bi,Zi
        -> Int               -- 答え

つまり、島どうしが連結なグラフをなせばよいので、UnionFindを使う方針は決まる。
ただし、島どうしをつなぐ道路（橋？）だけでなく、空路と海路も選択できるというアレンジに対応する必要がある。そこで

  • 空を仮想ノード番号 $0$ とし、空港とはノード $0$ と島を繋ぐ橋とみなす。
  • 海を仮想ノード番号 $N+1$ とし、港とはノード $N+1$ と島を繋ぐ橋とみなす。

これでコストの安い順に橋を架ける必要があるかUnionFindで判定してゆき、全て連結になったときのコスト合計を求める。

ただし、空港をひとつも作らない場合はノード $0$ は連結でないままで構わないし、港をひとつも作らない場合はノード $N+1$ は連結でないままで構わない。これを同時に判定するのは難しそうなので、

  • 橋だけで解決する。ノード $0$（絶対に接続されない）からノード $N$ までについて、連結成分が2個（$0$番のみとそれ以外）になる
  • 空も使って解決する。船は使わない。ノード$0$ からノード $N$ までについて全てが連結される
  • 海も使って解決する。飛行機は使わない。ノード $0$ （絶対に接続されない）からノード $N+1$ までについて、連結成分が2個($0$版のみとそれ以外）になる
  • 空も海も使う。ノード $0$ からノード $N+1$ までについて全てが連結される

の4通りとも計算し、最小値を選ぶことにする。

結果

制限時間が4秒あるが、20万ノードのUnionFindを4通りもするので、Data.Vector.Mutable.Unboxed を使ってIOモナドで計算する版を用いた。なので全体の関数もIOアクション化している。

橋の数が少なくとも $N-1$ はないと、全ての島を連結することはできない。

subでは最終的な分割数だけ数えている。全てを使う c4 において、例えば、実際には船は使わないで全体を連結できると分割数が1でなく2になってしまいそうだが、そのようなときはその場合に対応する c2 で最小値が正しく得られ、c4 では無駄に港を作ってコスト高になった結果が得られるだけで、結果には影響はない。

import Control.Monad
import Data.List

import qualified Data.Vector.Unboxed.Mutable as MUV
import Data.Maybe

abc270f :: Int -> Int -> [Int] -> [Int] -> [(Int,Int,Int)] -> IO Int
abc270f n m xs ys abzs =
  do
    c1 <- if m < pred n then return maxBound else sub n1 bridges 2
    c2 <- sub n1 ba 1
    c3 <- sub n2 bs 2
    c4 <- sub n2 bas 1
    return $ minimum [c1,c2,c3,c4]
  where
    n1 = succ n
    n2 = succ n1
    bridges = sort [(z,(a,b)) | (a,b,z) <- abzs]
    airs = sort [(x,(i, 0)) | (i,x) <- zip [1..] xs]
    seas = sort [(y,(i,n1)) | (i,y) <- zip [1..] ys]
    ba = merge bridges airs
    bs = merge bridges seas
    bas = merge ba seas

merge xxs@(x:xs) yys@(y:ys) =
  case compare x y of
    EQ -> x : y : merge xs ys
    LT -> x : merge xs yys
    GT -> y : merge xxs ys
merge [] ys = ys
merge xs [] = xs

sub :: Int -> [(Int,(Int,Int))] -> Int -> IO Int
sub n zabs len = do
  uf <- newUF n
  cost <- foldM (\cost (z,(a,b)) -> do
    m <- uniteUF uf a b
    return $ cost + maybe 0 (const z) m
    ) 0 zabs
  ds <- allDivisions uf
  return $ if length ds == len then cost else maxBound

-- UnionFind実装はAPIのみ示す
-- @gotoki_no_joe
type UnionFind = MUV.IOVector Int

-- 0からn-1までのn個の整数を対象としたUnion-Findを作る
newUF :: Int -> IO UnionFind

-- 二つの要素の属している分割を統合する
-- 統合を実際に行った場合、変更前の代表元の対を返す。左が新たな代表元
uniteUF :: UnionFind -> Int -> Int -> IO (Maybe (Int,Int))

-- 全ての分割について、その要素のリストを作る
allDivisions :: UnionFind -> IO [[Int]]

実際の結果はこちら。

追記 (2022-9-25)

「コストの安い順に、その辺が連結を行うなら使う」というUnionFindの応用には「クラスカル法」という名前がついている。

AtCoderにいるHaskellガチ勢の結果と比べてみると（敬称略）

誰 時間(ms) 空間(MB)
gksato 507 70
frtn_r 784 175
cojna 515 78
私 2986 391

と、一回り違う。
色々と試したが、allDivisions を使う代わりに、unionが起きた回数をカウントすることで分割数を管理し、最終的な分割数で成否を判定することで2587ms, 247MB とわずかに改善できただけだった。

他にやったこと：

  • 自作 merge をやめ、全体を毎回 Data.List.sort で整列 → TLE
  • UnionFindを4回の利用で共有して、メモリ割り当てを抑制 → 変化なし
  • IOVectorからSTVectorに変更 → 変化なし
  • 分割数が1になったところでループを脱出 → 変化なし
1
0
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?