SLPとCDAWG，RLBWTからString Attractorsが作れることを見る

この記事はデータ構造とアルゴリズム Advent Calendar 15日目の記事です．

はじめに

本記事は以下の論文

• Dominik Kempa, Nicola Prezza, At the roots of dictionary compression: string attractors. STOC 2018

の一部を紹介する内容になります．

string attractorsは辞書式圧縮アルゴリズムと関連した新しい概念です．
LZ法やBWT，SLPを用いた文法圧縮など，この世の中には様々な辞書式圧縮アルゴリズムがありますが，それらは（異なる手法で）ある同じ問題(string attractorsの生成)を解こうとしていることを示したり（すごい！！），他にもいろいろな進捗が生まれに生まれており，圧縮データ構造・圧縮アルゴリズムに興味がある人は大興奮といった感じじゃないでしょうか．
そんなわけでこのデータ構造とアルゴリズム Advent Calendar においても既にLZ圧縮法がstring attractorsを生成していることを解説した大変わかりやすい記事が，echizen_tm氏によって2日目に投稿されています．（テーマ，見事に被ってしまいましたね……）

この記事ではLZ以外の圧縮法とstring attractorsの関係，またおまけとして各圧縮法間のサイズの関係を紹介したいと思います．

String Attractorsの定義

本題に入る前にString attractorsの定義を確認したいと思います．（echizen_tm氏の記事と同じ例を使います．）

---

String attractosの定義
長さ$n$の文字列$T$に対して，$T$のポジションの部分集合$\Gamma = \{p_1, p_2, ..., p_\gamma \}$が以下の条件を満たすとき，$\Gamma$を$T$のstring attractorsと呼ぶ．

• $T$の任意の部分文字列$T[i..j]$に対し，$T[i..j] = T[i'..j']$かつ$p_k \in [i', j']$となるような$T[i'..j']$が必ず存在する（ここで$p_k \in \Gamma$）．

---

言い換えると，$T$の任意のdistinctな部分文字列の出現位置が$\Gamma$の要素を含むとき，$\Gamma$をstring attractorsと呼びます．

よくわからないと思うので以下の図を見てください．

上の図のように，$T = CDABCCDABCCA$に対して$\{4, 7, 11, 12\}$はstring attractorsになります．これは$T$に対する最小のstring attractorsです．

定義より明らかなように，最大のattractorsは全ての位置を含む集合$\{1, 2, \ldots, n\}$です．また同じく定義よりstring attractorsは必ず文字の種類数（上記の例だとA, B, C, Dの4種類）以上のサイズが必要です．

一般に最小のattractorsを求める問題は難しい¹のですが，様々な辞書式圧縮構造が最小string attractors問題の近似解を与えていることとみなせることが示されました．LZ77に関してはこちらの解説記事があるので，以下では文法圧縮(SLP)とCDAWG，RLBWTといった構造がstring attractorsを生成していることを確認したいと思います．
具体的には，

• 生成規則数$g$のSLPが与えられた時，サイズが高々$g$のstring attractorsを導ける．
• 枝数$e$のCDAWGが与えられた時，サイズ$e$のstring attractorsを導ける．
• Runの個数が$r$のBWTが与えられた時，サイズ$r$のstring attractorsを導ける．

ということを，ふわっとした感じで見ていきたいと思います．実装はありません．

SLP → String Attractors

まずはStraight Line Program (SLP)を用いて圧縮された文字列からString attractorsを求める方法を紹介したいと思います．

SLPの定義

文字列$T$を生成するような文脈自由文法を構成することで圧縮表現を実現する方法を文法圧縮と呼びます．今回はSLPと呼ばれる（簡単に言うと）一意な文字列を生成するようなChomsky標準形の文脈自由文法で文字列$T$を表現することを考えます．
Chomsky標準形とは，生成規則が

• $X \rightarrow AB$　（$X$と$A$, $B$はそれぞれ非終端記号）
• $X \rightarrow a$ （$a$は終端記号）
  の形になっているものです．

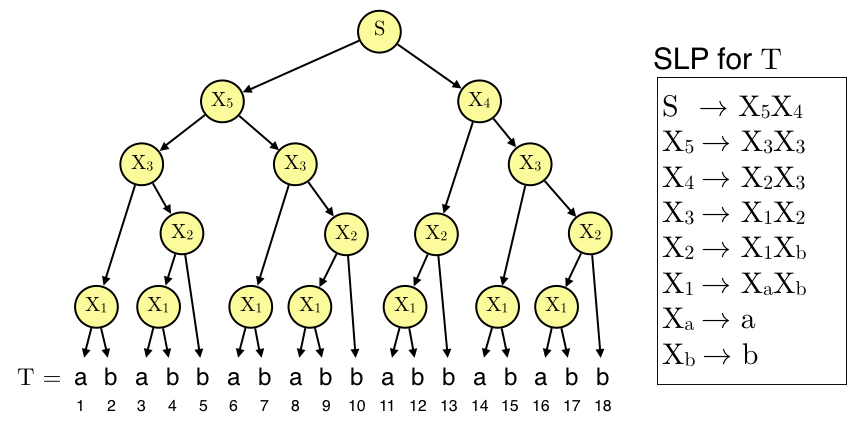
以下の図を見てください．

右の生成規則群が$T$を生成する文脈自由文法（$S$から展開することで$T$を復元可能），左の木構造がその構文木です．上記例では長さ18の文字列$T$を8つの生成規則だけで表現しており，このSLPは元文字列を圧縮しそうです²．

SLPサイズのstring attractorsの作り方

文字列$T$を生成するようなSLPが与えられた時，その生成規則数を$g$とすると，高々サイズ$g$のstring attractorsを構成することができます．

作り方は以下の通りです．

• 生成規則$X \rightarrow AB$に対して，非終端記号$A$が生成する部分文字列の末尾位置のいずれかをstring attractorsの要素とする．
• 生成規則$X \rightarrow a$に対して，文字$a$のいずれかをstring attractorsの要素とする．

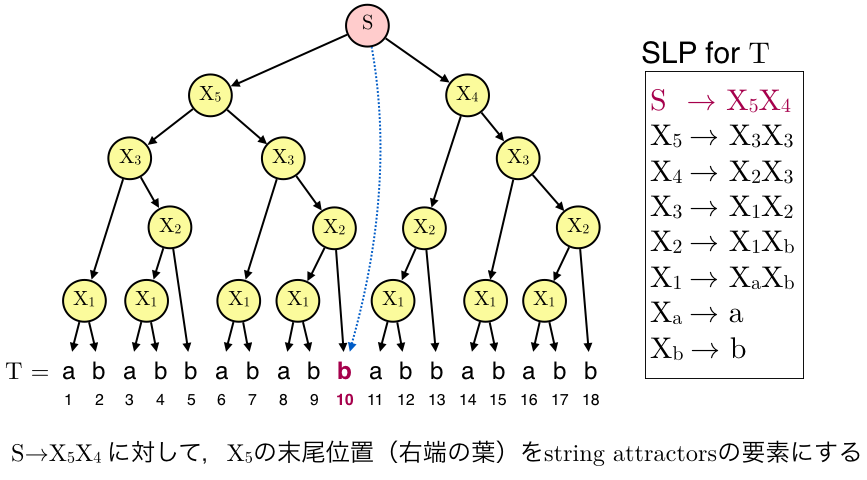
図で見てみます．

生成規則$S \rightarrow X_5X_4$について，$X_5$の末尾位置をattractorsの要素とします．生成規則$X_5$や$X_4$に関しても同様です（それぞれ位置5と13がattactorsの要素になる）．

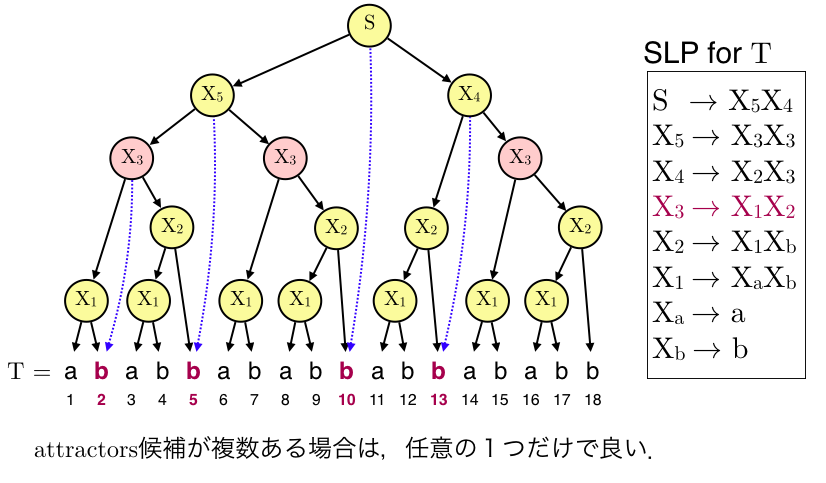
生成規則が複数の位置で部分文字列を生成する場合，その中の任意の１つだけをattractorsの要素に追加すれば良いです．（上記例だと，$X_3$に関して位置$2$と$7$, $15$がattractors候補となる．今回は$2$を追加）

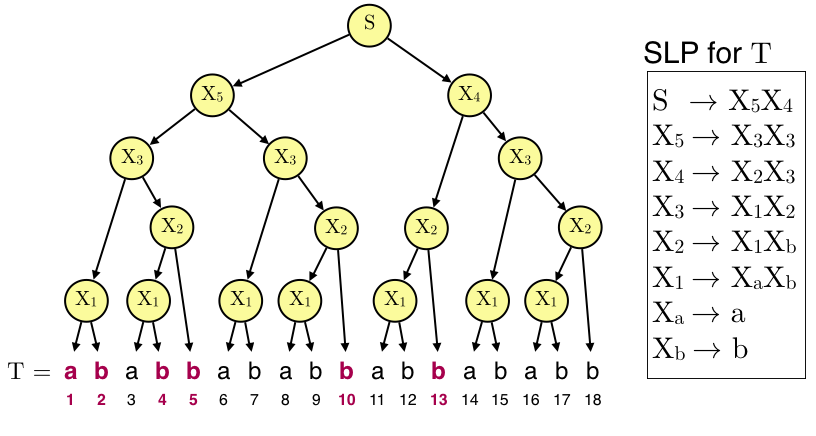
このアルゴリズムを全ての生成規則に関して適応していくと，最終的には位置$\{1,2,4,5,10,13\}$がstring attractorsとなります．（候補が複数ある場合は一番左の位置を採用）．

残念ながらこれは最小のstring attractorsではありません（例えば$\{1,5,10\}$はstring attractorsになります．（なりますよね……？））．

何故attarctorsになる？

上記アルゴリズムが何故attractorsを生成するか，厳密な証明は論文に任せて，図を使った簡単な解説をしようと思います．

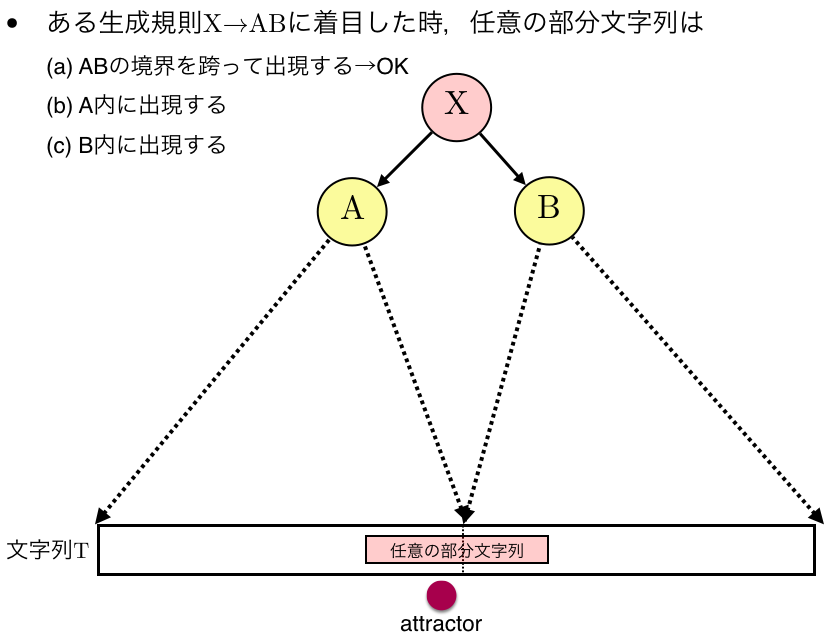
以下の図はある生成規則$X \rightarrow AB$とその規則に対応するattractorの位置を表しています．

上図のように記号AとBが生成する部分文字列の境界をまたがるように出現している部分文字列をこのattractorでカバーできます．

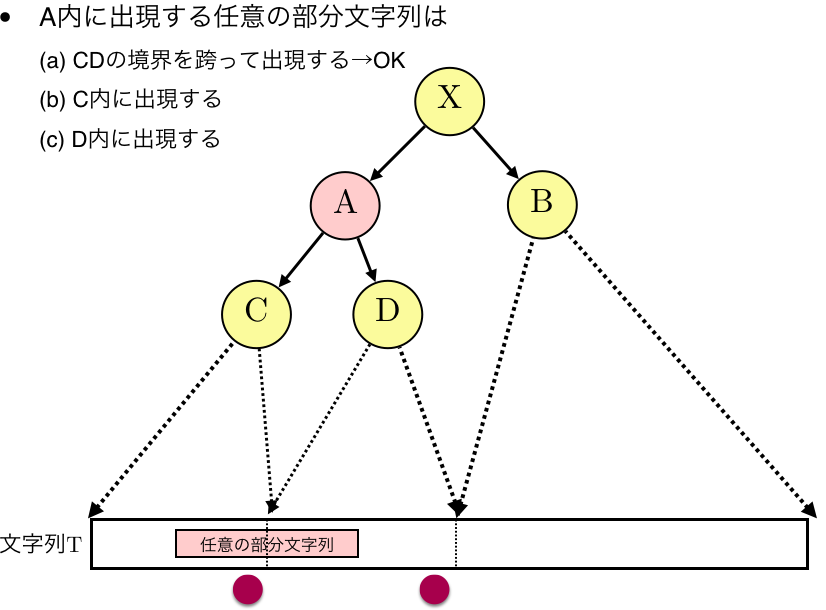
それ以外，例えばA内のみに出現するような部分文字列の場合，以下の図のように生成規則$A \rightarrow CD$に着目して同様のことが言えます．

これを再帰的に適応していけば，長さが2以上の任意の部分文字列が必ずいずれかの生成規則の境界をまたぐことが示せるため，その位置をstring attractorsの要素としておけば良いことが分かります．

Run-length SLPとCollage system

SLPの生成規則に加えて，$X \rightarrow A^k$（変数$A$の$k$回繰り返し）という形の規則を許したRun-length SLP(RLSLP)やさらにその拡張であるcollage systemに対しても同様の戦略で高々生成規則数サイズのstring attractorsを生成できます．

CDAWG → String Attractors

次に全文索引として利用されるCompact Directed Acyclic Word Graph (CDAWG)について見ていきたいと思います．

CDAWG

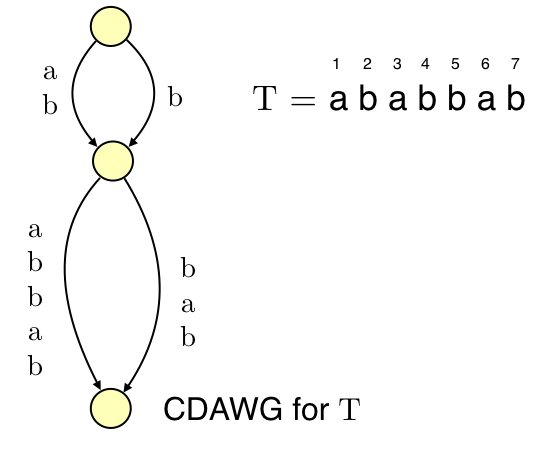
CDAWGは（簡単に言うと）与えられた文字列の全ての接尾辞をsinkノード（入次数０のノード）からのパスで表現するようなDAG構造です．以下の図は文字列$T = ababbab$に対するCDAWGです．

$T$の全ての接尾辞（$T$から先頭0文字以上削ったもの）がsinkノードからのパスで表現されています．すなわち，このDAG構造は接尾辞のみならず$T$中の任意の部分文字列をsinkからのパスで表現することができます．

この構造と文字列圧縮とがどう関係するのか？ ということなのですが，長さ$n$の文字列に対してCDAWGの辺数は最小$O(\log n)$になることが知られており（フィボナッチ文字列³に対して達成します），索引サイズをこの辺数で抑えることで，圧縮全文索引を構築することができます⁴⁵．CDAWGの辺数は正確に言うとmaximal repeatの右拡張数と呼ばれるものと一致するのですが，そこらへんの解説はこちらの記事で行なっています．

CDAWGサイズのstring attractorsの作り方

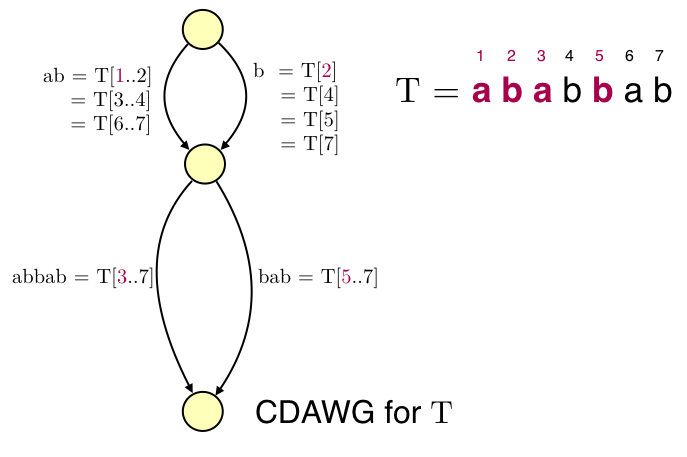
文字列$T$に対する辺数$e$のCDAWGが与えられた時，CDAWGの各辺ラベルの先頭文字位置をattractorsにすることで，サイズ$e$のstring attractorsを構成することができます．以下の図が例です．

上記図では各辺ラベルに対応する部分文字列を示し，その先頭文字の位置をattractorsにしています．残念ながらこの例のstring attractorsも最小ではないです（$\{3,5\}$だけでattractorsになる）．

なぜこの方法でattractorsができるかというと，
もともとCDAWGの定義より全ての部分文字列はsinkからのパスで表現されているため，すべての辺の先頭文字をattractorsにすることで任意の部分文字列がいずれかの辺から生成されたattoractorの位置を跨ぐことになるからです．

RLBWT → String Attractors

最後にRun-Length Burrows-Wheeler transform(RLBWT)について見ていこうと思います．
圧縮手法としてはLZと並んで有名だと思います．今回のreductionはBWTに関する前提知識が必要となってしまいSLPやCDAWGからのreductionと比べると難しいため，BWTについての解説記事（特にLF-mappingについて解説しているもの）を読んでからの方が理解できると思います．

RLBWTの定義

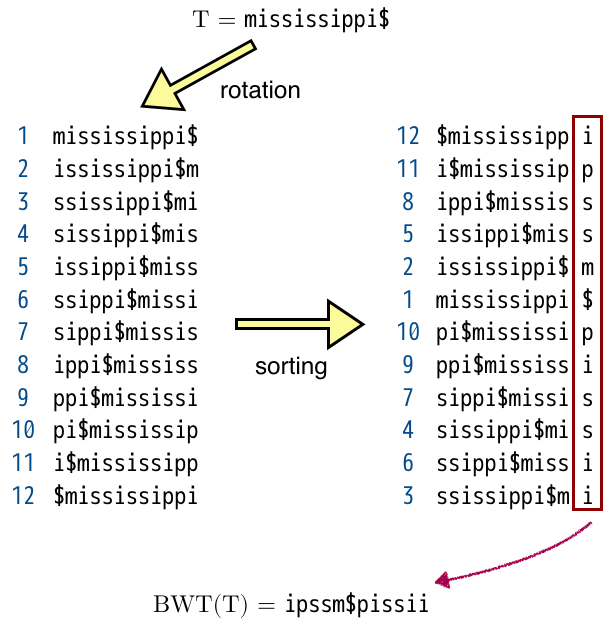
まずBWTを定義したいと思います．文字列$T$に対するBurrows-Wheeler transform $BWT(T)$は，$T$の全てのrotationをソートし，そのソート結果の末尾を連結したものです．以下の図を見てください．

末尾の文字$$$は他のどの文字よりも小さいとします．

こうして得られた$BWT(T)$は，同じ文字が連続して出現しやすいという性質を持ちます．そこでこのBWTに連長圧縮（Run-length compression）をかけたものがRLBWTです．
すなわち，$BWT(T)$に含まれるRunの個数（同じ文字が連続して出現するブロックの個数）が少ないほど圧縮できます．上の図の例だとRunは順に"$i$"，"$p$"，"$ss$"，"$m$"，"$$$"，"$p$"，"$i$"，"$ss$"，"$ii$"の8個になります．

Suffix arrayをご存知の方（ちょうど6日前のアドカレ記事で解説されている）はもう少し綺麗に定義できます．すなわち，

• $BWT(T)[i] = T[SA[i] - 1]$ ($SA[i] > 0$のとき)
• $BWT(T)[i] = T[n]$ ($SA[i] == 0$のとき)
  です．

RLBWTサイズのstring attractorsの作り方

BWTが与えられた時，各Runの先頭位置と末尾位置をattractorsにすることで，$run$の個数の2倍，$2r$サイズのstring attractorsを構築することができます．（論文内ではサイズ$r$のattractorsを構築できると主張しており，おそらくその通りなのですが，（私の勘違いの可能性が高いですが）なんだか引っかかるところがあるので，安全寄りに$2r$サイズの証明をやりたいと思います．あとで修正しますね．）（$2r$サイズの証明はarxivの旧バージョンで示されていたはずです．）

以下，具体例です．

上記図では各文字のrankを添字につけています．
かなり恣意的な例ですが，$BWT(T)$のRunの先頭・末尾の元文字列$T$上の位置をstring attractorsの要素にすることで，達成することができます．

簡単な証明として，任意の部分文字列が$T[i\ldots j]$がstring attractorsをまたぐような出現$T[i.. j] = T[i'..j']$を持っていることを示します．
$i=j$，すなわち長さ１の部分文字列の場合，各Runの先頭末尾をattractorsとして追加しているので，これは必ずattractorsを跨いで出現します．
次に$i < j$の場合を考えます．元文字列の全てのrotationをソートし，接頭辞が$T[i+1..j]$から始まる範囲を考え，これを[s,e]とします．範囲$BWT(T)[s,e]$に，$T[i]$ではない文字が含まれるならば，それはRunの境界を含む出現が存在することになるので，string attractorsを跨ぐことになります．範囲$BWT(T)[s,e]$が全て$T[i]$ならば$T[i+2..j]$を考え再帰的に上記の手続きを繰り返すことで必ずattractorsを跨ぐことを証明できます．（めちゃくちゃ悪文ですいません．．．あとで図を追加します．）

小さいstring attractosを作りたい時，結局LZ，BWT，SLP，CDAWGのどれを使えばいいのか？

最後に少しだけ話をかえて，各圧縮法のサイズの関係について紹介したいと思います．

結論から言うと，"だいたいの場合において"LZ factorizationによるstring attractorsの導出がこの中では一番小さいサイズになることが多いです．

• $z$: LZ77によるfactor数（自己参照あり）
• $r$: BWTのrunの個数
• $g$: 最小文法の生成規則数
• $e$: CDAWGの辺数
• $n$: 元の文字列$T$の長さ

とした場合，次のことが示されています．

• $e \geq max(z,r)$
• $e = \Omega(g)$
• $g = O(z \log(n/z))$

すなわち，$e$がもっとも大きく，$g$は必ず$z$よりも大きくなるという感じです．
BWTとLZ間についてですが，

• $T$がde Bruijn sequencesの場合，$r = \Omega(z \log n)$
• $T$がフィボナッチ文字列の場合，$z = \Omega(r \log n)$

という関係が示されているため，文字列の性質によってどちらが小さくなるかが決まります．
しかしながら，実験的には大体の場合において$z$がもっとも小さく，次点で$r$，$r$に勝ったり負けたりの$g$，他と比べるとかなり大きくなってしまう$e$という関係になっています．

そんなわけで，小さいstring attractorsを作りたい人！　おすすめの記事がありますよ．

LZ77 から string attractors を作る

実装も公開されていて最高……神……

まとめ

辞書式圧縮である文法圧縮（SLP）とCDAWG，RLBWTがstring attractorsを導出していることを確認しました．

String attractorsの面白いところは，（個人的には）サイズ$\gamma$のattractorsが与えられたとき，それらを用いてランダムアクセス可能なデータ構造や圧縮全文索引を作成できるところなのですが，それはまた別の機会に（もしくは私以外の誰かが）解説したいと思います．

お疲れ様でした．

1. 決定問題版がNP-Complete ↩

2. 符号化まで考えると圧縮していると言うのは嘘ですが……（$T$中に$a$と$b$しか出現していないため，元文字列はほとんどbit列） ↩

3. $F_1 = a, F_2 = b, F_n = F_{n-1}F_{n-2}$で定義される文字列 ↩

4. Takuya Takagi, Keisuke Goto, Yuta Fujishige, Shunsuke Inenaga, Hiroki Arimura, Linear-Size CDAWG: New Repetition-Aware Indexing and Grammar Compression. SPIRE 2017 ↩

5. Djamal Belazzougui, Fabio Cunial, Fast Label Extraction in the CDAWG. SPIRE 2017 ↩