これは「文字列アルゴリズム Advent Calendar 2016」23日目の記事です。

前回の記事は@okateimによる「Range minimum Query」でした．
次回の記事は@kgotoによる「なぜ12月21日が回文の日なのかを考えてみた」です．

はじめに

goonewです．文字列アルゴリズム，特に文字列に対する索引について研究しています．

よく知られた全文索引として，Suffix tree(接尾辞木)とSuffix array（接尾辞配列）が存在します．両者のいいとこを組み合わせるとSuffix trayと呼ばれる索引になり，イカす（クエリ時間計算量が改善される），という論文紹介がこの記事です．

該当する論文は
Richard Cole, Tsvi Kopelowitz and Moshe Lewenstein. Suffix trays and Suffix Trists: Structures for Faster Text Indexing. Algorithmica 72(2), 450-466, 2015.
です[1]．国際会議版はICALP2006に通っているようです．

本記事の他に，Suffix trayを紹介したものとして，
- Erik Demaineの講義動画
- Oren Weimannの講義資料(pdf)
等が存在します．

この記事にはSuffix trayを解説するために必要な知識として，以下の事項についての簡単な解説があります．
- Suffix tree
- Suffix array
- LCP array

やっていきましょう．

パターンマッチング・全文索引

テキスト$T$の中からパターン$P$を探す問題をパターンマッチングと呼びます．
以下のテキスト$T$からパターン$P = $ "鰛鰯魦" を探してください．

テキスト$T = $ "鯆鰯鰻鰯鰻魦鰛鰯魞魞鰛魦鰛魦鰛魦鰛魦魦鰯鰯鯆鰯鰻鰯鰻魦鰛鰯魞魞鰛魦鰛魦鰛鰯魦鰛魦魦鰯鰯"

見つかりましたか？こういう感じの問題です．

テキスト$T$の長さを$n$，パターン文字列$P$の長さを$m$とすると，KMPのようなテキストをすべて舐めるアルゴリズムで$O(n + m)$時間で解くことができます．

入力テキストに対し前処理を行い，全文索引と呼ばれるデータ構造を作成することで，このパターンマッチングをより高速に解くことができます．

Suffix treeはパターンマッチングを$O(m \log \sigma)$時間，
Suffix array(+ LCP array)は$O(m + \log n)$時間で解きます．
それらを組み合わせると$O(m + \log \sigma)$を達成できるというのがSuffix trayです．
$\sigma$はアルファベットのサイズ（文字の種類数）で，$n$を超えないです．
つまり，より速くパターンマッチングを解けるわけです．
気持ちがわかりましたか？

以下で，Suffix treeとSuffix array，Suffix trayの順で紹介します．

（特に，パターンが存在するか否かをyes/noで返す問題はmember queryと呼ばれます．他に，出現回数を返すcountや出現位置をすべて返すlocateなどがあります．以降はmember queryを考えます．）

Suffix Tree

アルファベットサイズ（文字シンボルの種類数）$\sigma$，長さ$n$のテキスト$T$を考えます．¹
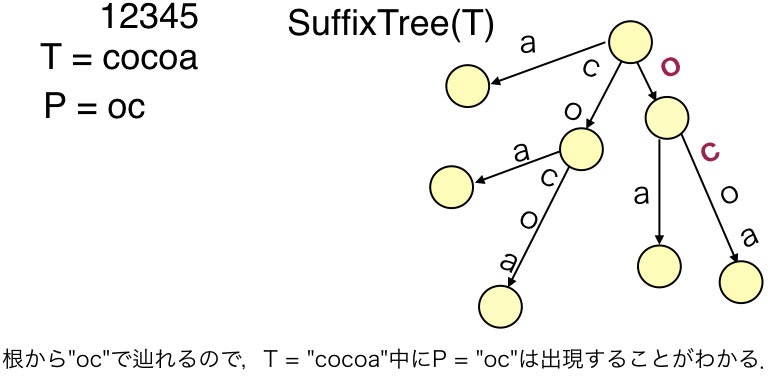
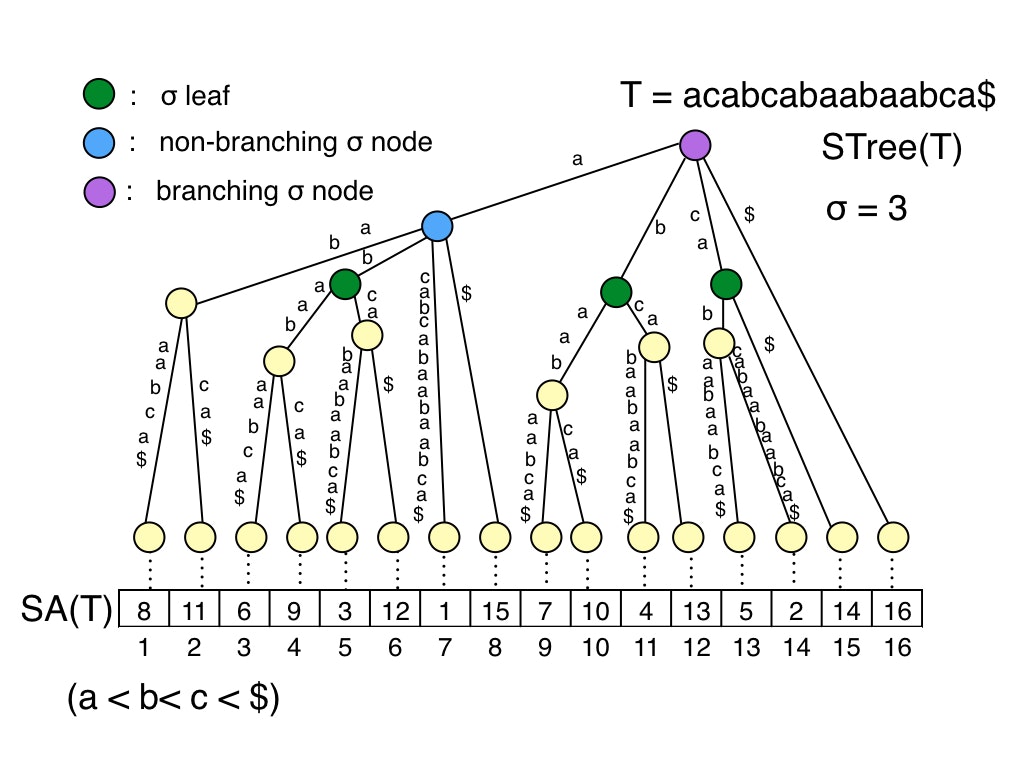
テキスト$T$に対するSuffix treeは，$T$のすべての接尾辞を根からのパスで表現したコンパクトトライです．
（文字列$T$の接尾辞とは，$T$を先頭から0文字以上削ったものです．）
以下の図がそれです．

コンパクトトライというのは，枝に文字列がついた根付き木で，以下の特徴を満たすものです．
- 根を除く全ての内部ノードは2つ以上の子ノードを持つ．
- ある内部ノード$v$が持つoutgoing edge (子ノードへの辺)についているラベルの先頭文字はすべて異なる．

いいですね．
Suffix treeに必要な領域計算量を考えます．結論からいうと$O(n)$ wordsです．
証明のスケッチだけ書いておきます．葉ノードの個数は高々$n$個です．コンパクトライの定義より，各内部ノードは２つ以上の子を持つので，内部ノードの個数は最大$n-1$個だとわかります．よってノードの個数は$O(n)$個，したがって辺の本数も$O(n)$本になります．ラベルの総文字列長は$O(n^2)$に見えますが，各枝ラベルは入力テキスト$T$上の参照で表現できます．例えば上の図における$coa$という枝ラベルは，$T$の$3$番目から$5$番目までの文字列と表現できるので，枝ラベルは整数２つで表現できます．そんなわけでまとめて$O(n)$ wordsです．こんな感じです．

この接尾辞木を入力に対して線形時間で構築するアルゴリズムが知られています[2]．

Suffix tree上でパターンマッチングのクエリをかけましょう．
パターン$P$が存在するかどうかを調べたいときは，根からパターン$P$で木を辿れば良いだけです．
$m$文字辿るのに必要な時間は$O(m \log \sigma)$時間です．

なぜ log σ ?

思い出しておくと，$\sigma$はアルファベットのサイズ（文字シンボルの種類数）です．
Suffix tree上を$m$文字辿るのには$O(m)$時間で済みそうですが，各ノードから出ている最大$\sigma$個の枝から，適切なものを選ぶのに２分探索する必要があり，毎回$O(\log \sigma)$時間かかります．（アルファベットに全順序関係が定義されていることを仮定．）

これを回避する策として，各ノードに長さ$\sigma$の配列を持たせ，対応する子ノードへ定数時間でアクセスする方法が考えられますが，Suffix treeの領域計算量は$O(n\sigma)$ wordsになってしまいます．
別の策として，文字をkeyとして対応する子ノードをvalueにもつ辞書（ハッシュ）を各ノードに持たせる方法が考えられます．これならば定数時間・定数領域で子ノードへアクセス可能です．しかしながらDeterministicな辞書だと構築に$O(n \; min( \log \sigma, \log \log n ))$時間かかってしまいます[3]．（Randomizedな辞書を用いれば，線形時間で構築可能です．）

まとめると，Suffix treeを線形領域・線形時間で構築する場合，最悪決定性時間$O(m \log \sigma)$でパターンマッチングを解くことができます．

Suffix Array

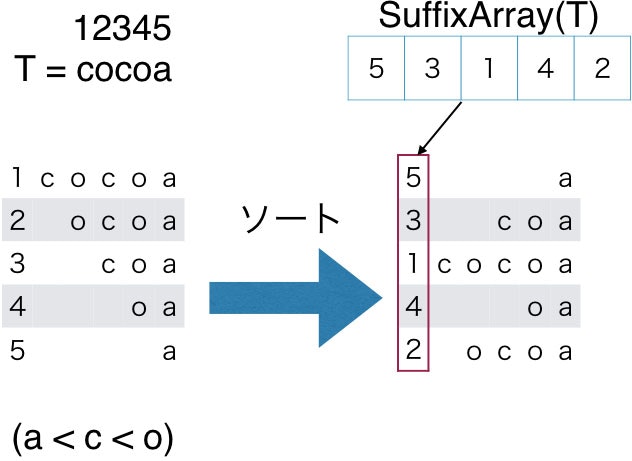
Suffix arrayは，与えられた入力テキスト$T$のすべての接尾辞をソートし，そのソート結果を添字番号の配列として持つものです．

以下の図をみてください．

Suffix arrayの領域計算量は，$n$個の整数が並んでいるだけなので$O(n)$ wordsです．
また，この配列を$O(n)$時間で構築できることが知られています[4,5,6]．

Suffix array上で，パターンマッチングのクエリをかけましょう．
あるパターン$P$が存在する場合，Suffix array上に対応する範囲が存在するはずです．
以下の図をみてください．

配列上の２分探索で達成するだけです．
つまり$O(m \log n)$時間です．
$\log n$がかかっているのが辛い感じなので，次の節で改善します．

LCP Array

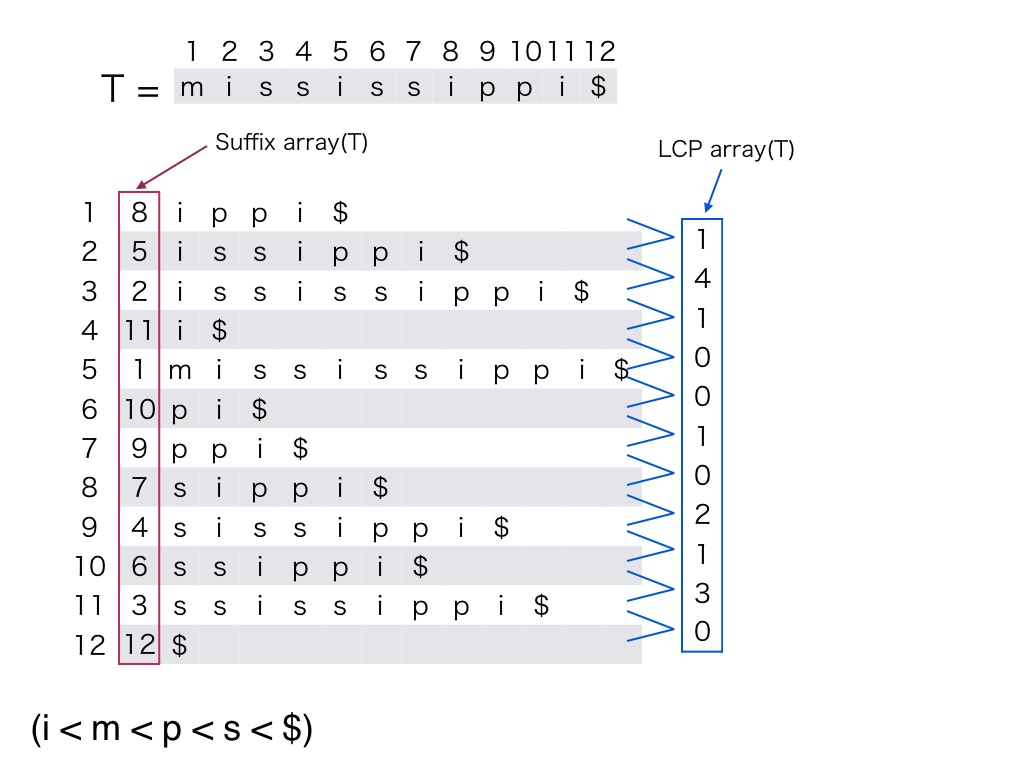
Suffix array上のパターンマッチングを高速に行うために，LCP array (Longest Common Prefix Array，最長共通接頭辞配列)というものを考えます．
LCP arrayとは，Suffix array上で隣あう接尾辞の共通接頭辞の長さを格納した配列です．以下の図を見てください．ちなみにSuffix arrayより線形時間で求めるアルゴリズムが知られています[7]．

Suffix arrayとLCP arrayを使って高速にパターンマッチングを行う方法は，echizen_tm氏のブログ記事で詳しく解説されています²．ので，そちらを参照してください．
参照しましたか?? そんなわけで，LCP arrayを用いることで$O(m + \log n)$時間でパターンマッチングを計算できます．よかったですね．
計算量の$O(m + \log n)$時間について，最初の項$m$はパターン長によるものであり，$\log n$の項は長さ$n$の範囲を２分探索するのにかかるコストということです．少しあとで使います．

Suffix Tray

ここまでで，Suffix treeとSuffix arrayについて簡単に見てきました．
Suffix trayはColeらによって提案された，Suffix treeとSuffix arrayを組み合わせたデータ構造です[1]．領域は$O(n)$ wordsで変わらず，パターンマッチングを最悪決定時間$O(m + \log \sigma)$で解くことができます．

とりあえず，雑にSuffix treeとSuffix arrayを組み合わせましょう．
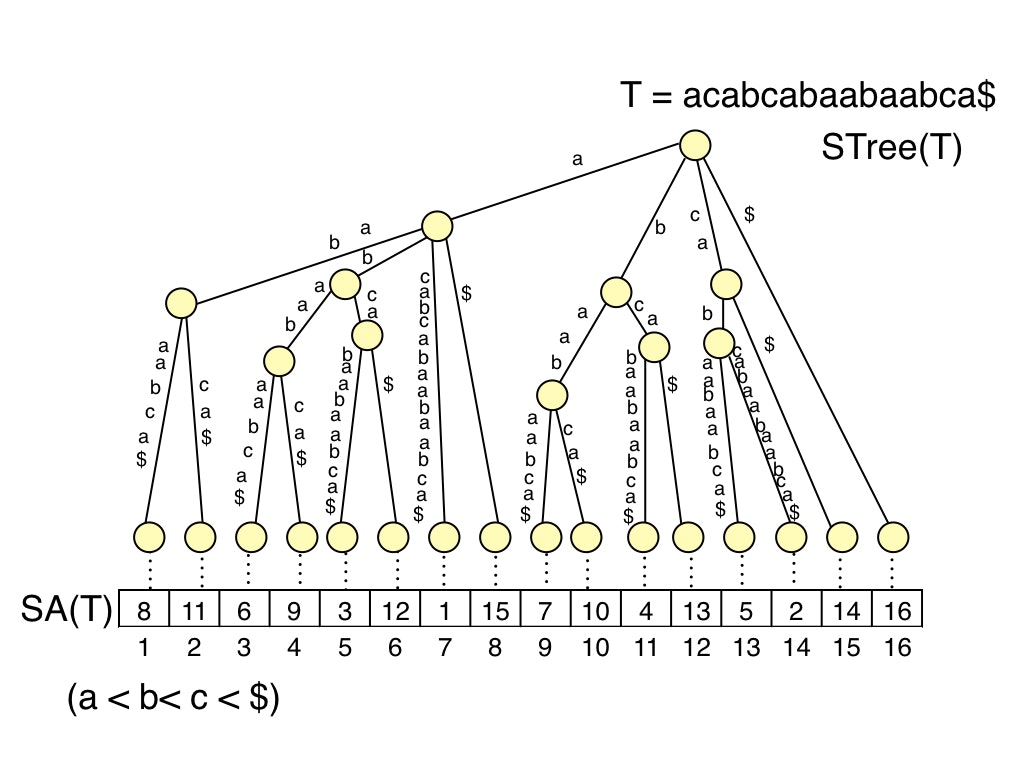
Suffix treeの枝が先頭ラベルでソートされていることを仮定すると，
Suffix treeの葉ノードはSuffix arrayと対応します．以下の図のような感じです．

Suffix treeのクエリ時間が$O(n \log \sigma)$である理由は，
最大$\sigma$個ある枝から正しいものを２分探索で選択する必要があるからでした．それを回避する方法として，各ノードが長さ$\sigma$の配列を持ち，定数時間で対応するノードへアクセスする方法がありましたが，領域計算量は$O(n \sigma)$ wordsになってしまいます．
それならば，Suffix treeを上手に間引いてノード数を$O(n / \sigma)$個にしてあげれば，たとえ各ノードが$\sigma$サイズの配列を持ったとしても線形領域で済みます．間引いた分はSuffix arrayで補うことでクエリを解きます．これがSuffix trayの基本的なアイデアです．

次の節で間引き方を見ていきます．

Heavy Node Decomposition

Suffix tree上のノード$v$が以下を満たすとき，$v$を$\sigma$ノードと定義します．
- $v$を根とする部分木に含まれる葉が$\sigma$個以上である．
$\sigma$ノードはHeavy nodeと呼ばれることもあります．
また$\sigma$ノードでないものをLightノードと定義します．

$\sigma$ノードをさらに以下の３つのタイプに分類します．
- $\sigma$ leaf: すべての子ノードが$\sigma$ノードでない．
- branching $\sigma$ノード: 2つ以上の$\sigma$ノードを子ノードとして持つ．
- non-branching $\sigma$ノード: 上記2つに該当しない$\sigma$ノード．

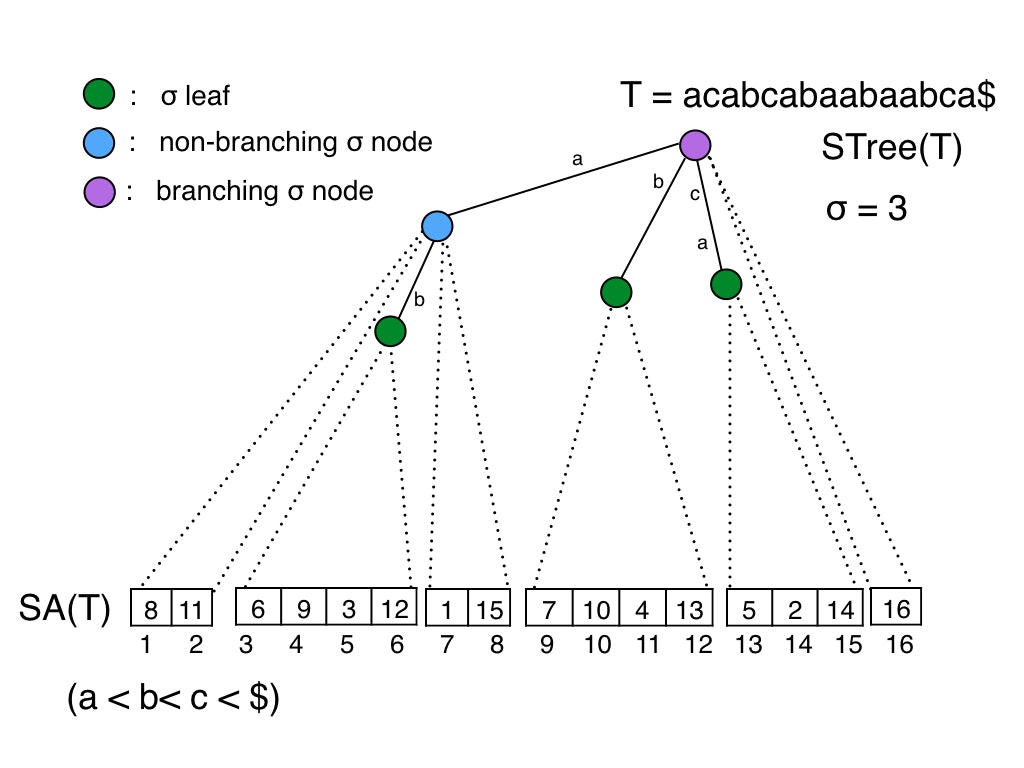
Suffix treeの各ノードをタイプ分けした例を以下に示します．論文[1]で用いられている例と同じものです．

こうして得られたbranching$\sigma$ノードですが，
Suffix tree上に$O(n / \sigma)$個しか存在しないことがわかります．
理由としては，$\sigma$ leafが高々$(n / \sigma)$個しか存在しないからです．（$\sigma$ノードの定義を思い出すと，部分木の葉ノードの数が$\sigma$個以上でした．）
この分解を，いま私が勝手にHeavy node decompositionと名付けました．最近いろいろ使われています³．
branching$\sigma$ノードに対しては，サイズ$\sigma$の配列をもたせ，$O(1)$時間での子ノードへのアクセスを実現します．
それ以外のノードに関しては，子ノードとして高々1つの$\sigma$ノードと$\sigma$個以下のLightノードしかもたないことがわかります．Lightノードの集合は2つのSuffix intervalで表現することができます（以下の図を見てください）．ラベルをもつ子は１つだけです．つまり，適切な枝を選ぶのに必要なコストは$O(1)$です．

Suffix Interval

上記の図では，根ノードから対応するSuffix intervalまで$O(m)$時間で到達することができます．
Suffix intervalはSuffix arrayのある範囲です．このIntervalの最大長を考えてみます．$O(\sigma ^2)$サイズです．なぜかというと，ある$\sigma$ノードは，最大$\sigma$個の$light$ノードを持ちます．$light$ノードの定義は，自分自身を根とする部分木の葉ノードが$\sigma$個未満のノードでした．よって，$\sigma$個のLightノードが各々$\sigma$個の葉を持つとして，Suffix Intervalはもともとの葉ノードと一致していますから，最大$\sigma ^2$サイズのIntervalをもつことになります．

Suffix arrayのパターンマッチングにかかる時間計算量を思い出すと，$O(パターン長 + \log (Interval長))$でした．
つまり，Suffix trayのInterval内での検索時間計算量は$O(m + \log \sigma ^2) = O(m + \log \sigma)$になります．
Suffix trayの根からパターン$P$に対応するIntervalまでは$O(m)$で到達できますから，パターンマッチングは合計で$O(m) + O(m + \log \sigma) = O(m + \log \sigma)$時間です！やったあ．Suffix treeやSuffix arrayよりも（理論上）速くなりました！

ちなみに構築も線形時間です．Suffix tree，Suffix arrayともに線形時間構築できますし，なんとなくそんな気がしますね．

結論

そんなわけで，Suffix trayは線形時間・線形領域で構築でき，パターンマッチングを$O(m + \log \sigma)$最悪決定時間でサポートします．ちなみに同論文では，Suffix arrayの部分をLinked listに変更しオンライン構築を可能にしたSuffix tristも紹介されています．

日本時間だとクリスマスが終わっており，アドベントカレンダー的には遅刻ですが，アメリカ領サモアではまだ２５日なので，これにてよしとします．
メリークリスマス．めでたいですね．

参考文献

[1] Richard Cole, Tsvi Kopelowitz and Moshe Lewenstein. Suffix Trays and Suffix Trists: Structures for Faster Text Indexing. Algorithmica 72(2), 450-466, 2015.
[2] Martin Farach-Colton, Paolo Ferragina and S. Muthukrishnan. On the sorting-complexity of suffix tree construction. J. ACM 47(6), 987-1011, 2000.
[3] Milan Ruzic. Constructing Efficient Dictionaries in Close to Sorting Time. In Proc. ICALP (1), 84-95, 2008.
[4] Juha Kärkkäinen, Peter Sanders, Stefan Burkhardt. Linear work suffix array construction. In J. of the ACM, 53(6), 918-936, 2006.
[5] Dong Kyue Kim, Jeong Seop Sim, Heejin Park, Kunsoo Park. Constructing suffix arrays in linear time. J. Discrete Algorithms, 3(2-4), 126-142, 2005.
[6] Pang Ko, Srinivas Aluru. Space efficient linear time construction of suffix arrays. J. Discrete Algorithms, 3(2-4), 143-156, 2005.
[7] Toru Kasai, Gunho Lee, Hiroki Arimura, Setsuo Arikawa and Kunsoo Park. Linear-Time Longest-Common-Prefix Computation in Suffix Arrays and Its Applications. In Proc. CPM2001, 181-192, 2001.
[8] Udi Manber, Eugene W. Myers. Suffix arrays: A new method for on-line string searches. SIAM J. on Computing, 22(5), 935-948, 1993.
[9] Fischer, J., Gawrychowski, P. Alphabet-dependent string searching with wexponential search trees. In Proc. CPM2015, 160–171, 2015.
[10] Takuya Takagi, Shunsuke Inenaga, Hiroki Arimura. Fully-online Construction of Suffix Trees for Multiple Texts. In Proc. CPM2016, 22:1-22:13, 2016.

文字列大好き人間のために書いておくと，整数アルファベットを仮定します．文字列大好き人間以外は無視してください． ↩
該当記事ではLCP array上でRmQを計算することで任意の2つの接尾辞のLCP長を定数時間で求めています．RmQを用いない方法が[8]で紹介されてます．Suffix array上の探索で聞かれる区間の種類は，幅１の区間が$n$個，幅2の区間が$n/2$個，幅4の区間が$n/4$個...という感じなので，高々$2n$個しかありません．そのため，論文[8]では必要な$2n$個のLCP値をすべて計算しています．[8]では$O(n \log n)$時間かかるとされていますが，実際は$O(n)$時間で計算することができます．結局RmQも[8]の方法も計算量は変わりませんが，一度計算してしまえば配列にアクセスするだけの[8]のほうが高速だと思います． ↩
Wexponential Search tree[9]などがあります．また，Heavy node decomposition上でSuffix tree oracleと呼ばれるデータ構造が提案されており[1, 9]，そのvariantが文字列集合に対するSuffix treeのオンライン構築などに利用されています[10]． ↩

Suffix Tree + Suffix Array = Suffix Tray