最近フーリエ解析の授業課題で「フーリエ変換を使った技術に関連したことについて何でもいいからレポート出してね」と言われたので作成してみました。
pythonの環境構築をわざわざやるのも面倒だったので基本的にGoogle Colaboratoryを使っています。
実装方針と理論
以下の方針で作成しました。- 画像の輪郭を検出
- 輪郭に対し任意の間隔で点を作成
- 点群を離散フーリエ変換
- フーリエ級数展開により形状近似
1,2の操作として、エッジの検出にはCanny法のライブラリを用いました。
3の操作については, 高速フーリエ変換を実装しました。高速フーリエ変換については以下で詳しく説明します。
fftなんてnumpy使えばいいと思いますが、授業課題なので丁寧に
高速フーリエ変換(fft)の理論と実装
まず, 離散フーリエ変換は以下の式で定義されます。$$X(k)=\sum_{n=0}^{N-1}{x_ne^{-\frac{2\pi nkj}{N}}}\ (k=0,\ 1,2\ldots,\ N-1)$$
今回のプログラムでは、離散フーリエ変換の手法として基数2の時間間引き形の高速フーリエ変換を用いました。
時間間引き形アルゴリズムでは、 $x_n$ を偶数番と奇数番に分けて考えます。
$W_N=e^{-\frac{2\pi j}{N}}$とおくと、定義より
$$X\left(k\right)=\sum_{n=0}^{\frac{N}{2}-1}{x\left(2n\right)W_N^{2nk}}+\sum_{n=0}^{\frac{N}{2}-1}{x\left(2n+1\right)W_N^{(2n+1)k}}$$
ここで, $f_{even}=x\left(2n\right),\ f_{odd}=x(2n+1)$ とすると $W_N^{2nk}=W_{\frac{N}{2}}^{nk}$ より
$$X\left(k\right)=\sum_{n=0}^{\frac{N}{2}-1}{f_{even}W_{\frac{N}{2}}^{nk}}+\sum_{n=0}^{\frac{N}{2}-1}{f_{odd}W_{\frac{N}{2}}^{nk}}$$
$$F_even\ (k)\ =\sum_{n=0}^{\frac{N}{2}-1}{f_{even}W_{\frac{N}{2}}^{nk}} $$
$$F_odd\ (k)\ =\sum_{n=0}^{\frac{N}{2}-1}{f_{odd}W_{\frac{N}{2}}^{nk}}$$
よって、
$$X\left(k\right)=F_{even}\left(k\right)+W_N^kF_{odd}(k)$$
定義よりX(k)は $k=0,\ 1,2\ldots,\ N-1$ であるから $W_N^k=W_N^{k-\frac{N}{2}}$ より
$$X\left(k\right)=F_{even}\left(k\right)+W_N^kF_{odd}\ \ \left(0\le k\le\frac{N}{2}-1\right)$$
$$X\left(k\right)=F_{even}\left(k-\frac{N}{2}\right)-W_N^{k-\frac{N}{2}}F_{odd}\left(k-\frac{N}{2}\right)\ \ \left(\frac{N}{2}\le k\le N-1\right)$$
この結果を用いてfft関数の実装を行います。
#高速フーリエ変換関数（時間間引き形のfftを採用）
def fft(x_n):
N = len(x_n)
n = N//2
if N == 1:
return x_n[0]
f_even = x_n[0:N:2]
f_odd = x_n[1:N:2]
F_even = np.array(fft(f_even))
F_odd = np.array(fft(f_odd))
#0<=k<=N/2-1のWを計算
W_N = np.exp(-1j * (2 * np.pi * np.arange(0,n)) / N)
X_k = np.zeros(N, dtype ='complex')
print(F_even + F_odd * W_N)
X_k[0:n] = F_even + F_odd * W_N
X_k[n:N] = F_even - F_odd * W_N
return X_k
実装
以下、実装したコードです。改めて見ると汚いですね。ライブラリと1,2の操作
from numpy.matrixlib.defmatrix import N
from matplotlib import image
import cv2
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy import integrate
from functools import partial
from scipy import interpolate
##画像から輪郭を検出し、点群の座標データを持つcsvを作成する関数
def create_csv(img):
#輪郭（エッジ）の検出
edges = cv2.Canny(img, 100, 200)
#エッジの確認用画像を出力
cv2.imwrite("edges.jpg", edges)
#エッジの座標値を求める
points = np.where(edges == 255)
y = points[0]*(-1)
x = points[1]
#画像の中心を原点にそろえる
height, width = img.shape[:2]
x = x - width/2
y = y + height/2
#配列を極座標順にソート
x,y = sort(x,y)
#csvファイルへの書き込み
y_reshape = y.reshape(1, y.size)
x_reshape = x.reshape(1, x.size)
blank = np.arange(x.size)
blank = blank.reshape(1, blank.size)
with open("edges.csv", 'w') as csv_file:
np.savetxt(csv_file, x_reshape, fmt="%.0d", delimiter = ",")
np.savetxt(csv_file, y_reshape, fmt="%.0d", delimiter = ",")
np.savetxt(csv_file, blank, fmt="%.0d", delimiter = ",")
csv_file.close()
#極座標を利用して座標を並べ替える関数
def sort(x, y):
x = np.array(x)
y = np.array(y)
rad = np.arctan2(y,x)
index = np.argsort(rad)
sort_x = x[index]
sort_y = y[index]
return sort_x, sort_y
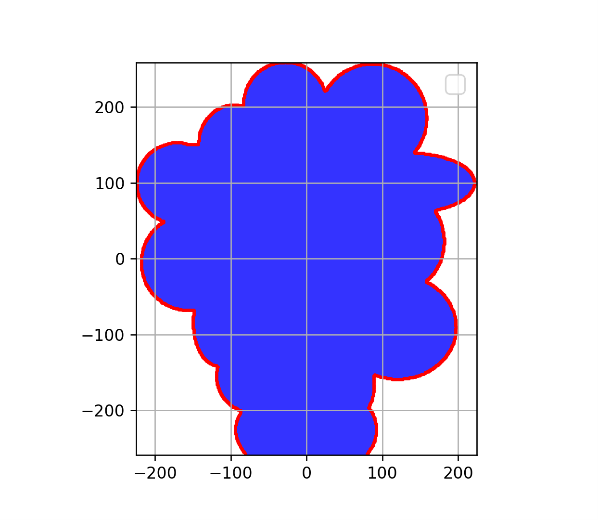
# csvファイルから散布図を作成し、画像と共に表示する関数（確認用）
def plot_scatter(csv_file,img):
df = pd.read_csv(csv_file, header=None)
#print("df ->" + str(df))
point_X = df.iloc[0, :].values.tolist()
point_Y = df.iloc[1, :].values.tolist()
height, width = img.shape[:2]
ax = plt.figure(num=0, dpi=240, figsize=(height/100,width/100)).gca()
ax.set_xlim(width/(-2),width/2)
ax.set_ylim(height/(-2), height/(2))
ax.scatter(point_X, point_Y, s=1, color="red") #, label=file_name)
ax.plot(point_X, point_Y,linestyle="None")
ax.set_aspect('equal', adjustable='box')
ax.imshow(img,extent=[*ax.get_xlim(), *ax.get_ylim()],alpha=0.8)
plt.grid(True)
plt.legend(loc='auto', fontsize=15)
plt.savefig("csv_plot.png")
plt.show()
plt.close()
3, 4の操作（先程のfftを使っています）
#フーリエ級数展開を行う関数
def fft_integral(X_k,N,x_n):
center_X = len(X_k) // 2
X_k = X_k[center_X - N : center_X + N+1]
ts = np.linspace(
0.0, 2.0 * np.pi, len(x_n)
) - np.pi
f = []
for t in ts:
temp = np.array(
[X_k[i] * np.exp(1j * k * t) for i, k in enumerate(range(-N, N+1))]
)
f.append(temp.sum())
f = np.array(f)
return f
def fourier_transform(csv_file, img):
df = pd.read_csv(csv_file, header=None)
x_n = df.iloc[0,:].values + df.iloc[1,:].values * 1j
fig, ax = plt.subplots(figsize=(8, 8))
ax.plot(x_n.real, x_n.imag)
plt.show();
#高速フーリエ変換を行う
X_k = np.fft.fftshift(fft(x_n)) / len(x_n)
#2～20次まで計算する
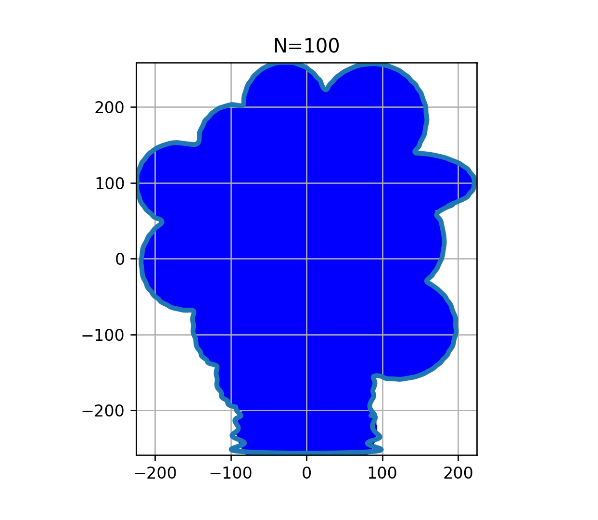
for N in [2, 5, 10, 15, 20, 50, 100]:
f = fft_integral(X_k,N,x_n)
plot_f(img, f, N)
def plot_f(img, f, N):
height, width = img.shape[:2]
ax = plt.figure(num=0, dpi=240, figsize=(height/100,width/100)).gca()
ax.set_xlim(width/(-2),width/2)
ax.set_ylim(height/(-2), height/(2))
ax.set_title("N=" + str(N))
ax.imshow(img,extent=[*ax.get_xlim(), *ax.get_ylim()])
ax.plot(f.real, f.imag, lw=3)
ax.grid()
plt.savefig("result_" + str(N) + ".png")
plt.show();
あとは実行するだけです。
def main():
#実行プログラム
img_file = "sample.png"
csv_file = "edges.csv"
img_file = cv2.imread(img_file)
create_csv(img_file)
plot_scatter(csv_file, img_file)
fourier_transform(csv_file, img_file)
if __name__ == '__main__':
main()
結果
入力画像（sample.png）とエッジ検出の出力結果は以下の通りです.
各次数の出力結果は以下の通りです（数が多いのでN=2,10,100のみ）
「次数が大きい方が精度が高い」という結果が良く分かりますね。
余談
せっかくフーリエ級数の輪郭近似プログラムを作成したので不連続点を作成しギブス現象の確認も行ってみました。
