はじめに
・学習メモレベルですので、理解が及んでいない部分はご容赦下さいませ。
・主に本書が何を言っているのかを解説的に書いてみる。
・式番号は本書に従っています。
4.1 観測データの線形変換
流れとしては、観測データを確率変数とみなしたうえで必要な統計量を定義し、それらを活用し観測データの線形変換を行っている。線形変換は特徴を組み合わせる時によく利用され、その変換後の平均値と共分散行列を求めることは、確率分布によらず成り立つので極めて重要な考え方である。
本節では、観測データを確率変数と捉えたうえで分布の操作を行うが、それら操作は線形変換によるものですよということ。
4.1.1 平均ベクトルと共分散行列
観測データは${\bf x}=(x_1,\cdots,x_d)^T\in{\mathcal R}^d$、その確率分布を$p({}\bf x)$とする。
${\bf x}$実数全体で連続した値をとる、とういうこと。
-
平均ベクトル(各特徴ごとの平均値を並べたもの)
$$\textbf{μ}=(\mu_1,\cdots,\mu_d)^T=(E[x_1],\cdots,E[x_d])^T$$ -
期待値($i$番目の特徴の期待値、連続確率変数のため積分をとる)
$$\displaystyle E[x_i]=\mu_i=\int_{-\infty}^\infty x_ip(x_i)dx_i$$ -
周辺確率($i$番目の特徴を表す確率変数$x_i$の確率分布)
$$\displaystyle p(x_i)=\int_{-\infty}^\infty \cdots \int_{-\infty}^\infty p(x_i,\cdots,x_d)dx_1\cdots dx_d$$ -
平均ベクトル(データがN個 {${\bf x_1},\cdots,{\bf x}_d$}の場合の算術平均)
$$\displaystyle{\bf μ}=\overline {\bf x}=\frac{1}{N}\sum_{i=1}^N {\bf x}_i$$
- 共分散行列(平均ベクトル周辺にある観測データ分布の広がり方)
\begin{align} {\bf \Sigma} & =Var[{\bf x}]= E[({\bf x} - {\bf \mu})({\bf x} - {\bf \mu})^T] \\
& = E \left\{
\left(
\begin{array}{c}
x_1 - \mu_1 \\
\vdots \\
x_d - \mu_d
\end{array}
\right)
(x_1 - \mu_1, \ldots , x_d - \mu_d)
\right\} \\
& = \left(
\begin{array}{ccc}
E\{(x_1 - \mu_1)(x_1 - \mu_1)\} & \cdots & E\{(x_1 - \mu_1)(x_d - \mu_d)\} \\
\vdots & \ddots & \vdots \\
E\{(x_d - \mu_d)(x_1 - \mu_1)\} & \cdots & E\{(x_d - \mu_d)(x_d - \mu_d)\} \\
\end{array}
\right) \\
& = (\sigma_{ij}) = \left\{
\begin{array}{ll}
i = j & 分散 \\
i \neq j & 共分散
\end{array}
\right.
\end{align}
\tag {4.1}
-
共分散行列の各要素$\sigma^2$の計算(${\bf x}$が連続量の場合)
$i$番目と$j$番目の特徴の同時確率を用いて計算される。
$$\sigma_{ij}=E[(x_i-\mu_i)(x_j-\mu_j)]=\iint(x_i-\mu_i)(x_j-\mu_j)p(x_i,x_j)dx_idx_j \tag {4.2}$$ -
共分散行列の各要素$\sigma^2$の計算(データが$N$個与えられている場合)
$n$番目のデータの$i$番目の特徴を$x_{ni}$、$j$番目の特徴を$x_{nj}$で表す。
$$\sigma_{ij}=E[(x_i-\mu_i)(x_j-\mu_j)]=\frac{1}{N}\sum_{n=1}^N(x_{ni}-\mu_{i})(x_{nj}-\mu_j)\tag {4.3}$$ -
相関係数($i$番目と$j$番目の相関係数$\rho_{ij}$)
$$\rho_{ij}=\frac{\sigma_{ij}}{\sigma_i \sigma_j}\tag {4.4}$$
必要知識(おさらい)
-
分散
$$Var[x]=E[(x-\overline x)^2]$$ -
期待値の性質
・$E[aX]=aE[X]$
・$E[X+a]=E[X]+a$
・$E[X+Y]=E[X]+E[Y]$
・$XとYが独立なら、E[XY]=E[X]E[Y]$ -
分散の性質
・$V[aX]=a^2V[X]$
・$V[X+a]=V[X]$
・$XとYが無相関なら、V[X+Y]=V[X]+V[Y]$
・$V[X]=E[X^2]-E[X]^2$
4.1.2 標準化
個々の特徴は測定単位の取り方で、数値だけを見たときにスケール差が生じる(ex.5[g] vs 22000[μm])。そのため分布の形状も変化してしまう。そこで測定単位の違いによる影響を取り除ことが標準化のモチベーションである。
標準化では、個々の特徴を平均0・分散1にスケーリングする操作をいう。
まずは、特徴$x$の線形変換を$y=ax+b$としている。その時の$y$の平均と分散は下記で導出している。(一次元特徴の線形変換を一次関数とするデモンストレーション的な登場であると推察。)
\begin{align}E[y]&=E[ax+b]=aE[x]+b\\\
&=a\mu +b
\end{align} \tag{4.5}
\begin{align}
Var[y] &= E[(y-E[y])^2]=E[(ax+b-a\mu-b)^2]\\
&= E[a^2(x-\mu)^2]=a^2E[(x-\mu)^2]\\
&= a^2Var[x]=a^2\sigma^2
\end{align} \tag{4.6}
上の手順と全く同様に、線形変換を$x$の平均$\mu$と標準偏差$\sigma$(正規分布の標準化)を用いた${z}$とする。これを標準化という。
z=\frac{x-\mu}{\sigma}\tag{4.7}
ポイントは、この$z$も一次関数だから、上のデモンストレーションの線形変換を$y=ax+b$としたときみたいに、計算ができてるとういうこと。下の式で${z}$を、より一次関数っぽく変形し確認。
z=\frac{x-\mu}{\sigma}=\frac{1}{\sigma}x-\frac{\mu}{\sigma}
特徴ごとに標準化を行うことで、測定単位の影響がない特徴ベクトルを構成することができた。
また図のように2次元で考えた場合、楕円状にに分布しているデータの中心が標準化により原点に移動するが、これを中心化という。イメージとしては、$\frac{1}{\sigma}$でギュッと圧縮して、$-\mu$で中心まで平行移動している。
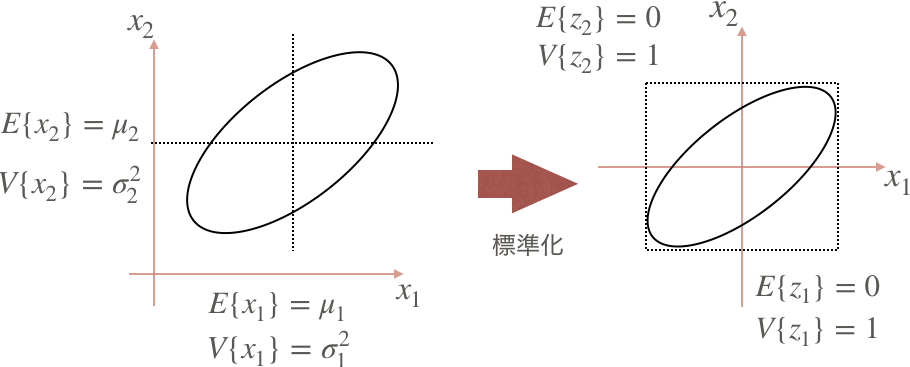
最後に、$z$の平均が0・分散が1になることを、期待値の定義を用いて証明する。
\begin{align}
E[z] &= E \left[\frac{x-\mu}{\sigma}\right]=\frac{1}{\sigma}(E[x]-\mu)=\frac{1}{\sigma}(\mu-\mu)\\
&= 0
\end{align}
\begin{align}
Var[z] &= Var \left[\frac{x-\mu}{\sigma}\right]=\frac{1}{\sigma^2}Var[x-\mu]=\frac{1}{\sigma^2}Var[x]\\
&= \frac{1}{\sigma^2}\sigma^2=1
\end{align}
平均が0・分散が1となっている。
4.1.3 無相関化
観測データの特徴間に相関があることは、マルチコなど基本的に好ましくない。しかし、無相関化のモチベーションは、その名の通りであるがデータ特徴間の相関を消すことである。
※無相関化は主成分分析に密接に関わっているが、4章時点ではまだ出ていないのでここでは天下り的に定義している。あまり追えなかった。。
本書内容に直接入る前に行列の対角化に、おさらい程度に触れておく。
行列の対角化
${\bf x}$の平均ベクトルを${\bf μ}$とおくと、${\bf x}$の分散共分散行列は${\Sigma=E[({\bf x} - >{\bf \mu})({\bf x} - {\bf \mu})^T]}$となる。
${\bf \Sigma}$は対称行列で、その性質により対称行列は直交行列${\bf P}$用いて対角化できる。
$${\bf \Sigma}=>{\bf P}^{-1}{\bf \Sigma}{\bf P}=>対角行列{\bf D}$$
・対角行列${\bf D}$の対角成分は${\bf \Sigma}$の各固有値(0以上の${\lambda_1,\lambda_2,\cdots,\lambda_n}$)
・${\bf P}$の各列ベクトルはの固有ベクトル
なお、${\bf P}$は直交行列なので${\bf P}^{-1}={\bf P}^T$なので、${\bf P}^T{\bf \Sigma}{\bf P}$と書いても同じ。
本書に戻る。
はじめに観測データから生成された${\Sigma}$の固有値問題を解く。
$${\Sigma}s={\lambda}s \tag{4.10}$$
解いて得られた$d$個の固有値、対応する固有ベクトルを${s_1,s_2,\cdots,s_d}$とし、これらを並べた行列${\bf S}$を定義する。
$${\bf S}=(s_1,s_2,\cdots,s_d) \tag{4.11}$$
ここで注目すべきは、共分散行列${\Sigma}$は実対称行列(dxd)であるということ。
実対称行列は重要な性質を多く持つ。各固有値は実数かつ固有ベクトルが直交している性質より、共分散行列の固有ベクトルは長さが1の正規直交基底となる。
※表記はクロネッカーのデルタ
{\bf S}_i^T{\bf S}_j = \delta_{ij}=
\begin{cases}
1(i=j) \\
0(i \neq j)
\end{cases}
すなわち、行列${\bf S}$は直交行列となる。
※”正規直交行列”、”回転行列”あたりは、天下り的に書かれているためか語弊を含んでおり、厳密には記載通りには定義できないらしい。
\begin{align}
({\bf S}^T{\bf S})_{ij} &= {\bf S}_i^T{\bf S}_j = \delta _{ij}\\\
\therefore{\bf S}^T{\bf S} &= {\bf I}\\\
\therefore{\bf S}^T &= {\bf S}^{-1}
\end{align}
上記を踏まえ、観測データ${\bf x}$を${\bf S}^T$で線形変換をすることを考える。
変換されたデータは,
$${\bf y}={\bf S}^T{\bf x}$$で与えられる。
このときの$y$の平均と共分散行列は、
$$\begin{align}E[{\bf y}]&=E[{\bf S}^T {\bf x}]={\bf S}^TE[{\bf x}]\
&={\bf S}^T{\mu}\end{align} \tag{4.12}$$
\begin{align}Var[{\bf y}]&=E[({\bf y}-E[{\bf y}])({\bf y}-E[{\bf y}])^T]\\\
&= E[({\bf S}^T{\bf y}-{\bf S}^T{\bf μ}])({\bf S}^T{\bf y}-{\bf S}^T{\bf μ}])^T]\\\
&= E[ \left\{ {\bf S}^T({\bf x}-{\bf μ}) \right\} \left\{ {\bf S}^T({\bf x}-{\bf μ}) \right\} ^T]\\\
&= E[{\bf S}^T({\bf x}-{\bf μ})({\bf x}-{\bf μ})^T{\bf S}]\\\
&= {\bf S}^{-1}[({\bf x}-{\bf μ})({\bf x}-{\bf μ})^T]{\bf S}\\\
&= {\bf S}^{-1}{\Sigma}{\bf S}
\end{align} \tag{4.13}
(4.12)の平均ベクトルは元のデータの平均ベクトルを線形変換したものになる。
(4.13)の共分散行列は、元のデータの共分散行列に線形変換行列とその逆行列を両側から掛けたものになる。
また、ここで$Var[{\bf y}]$(4.13)の最終形と最初に触れた対角化の式は同様の形をしていることが確認できる。つまり対角行列を得られる事になる。
{\bf S}^{-1}{\Sigma}{\bf S}={\bf \Lambda}=
\begin{pmatrix}
\lambda_1 & 0 & 0 & \cdots & 0\\
0 & \lambda_2 & 0 & \cdots & 0\\
0 & 0 & \lambda_3 & \cdots & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \cdots & \lambda_d
\end{pmatrix}
\tag{4.14}
したがって、共分散行列の固有ベクトルを並べた正規直交行列は、元のデータの分散行列を対角化するので、各固有値は対応する固有ベクトルの方向の分散となる。これを無相関化という。実際に共分散部分(非対角成分)が全て0の行列であるため、特徴間の相関がないことがわかる。
※9章の主成分分析を読み解く必要あり。
※「基底」を厳密に理解する必要あり。
4.1.4 白色化
無相関化をしただけでは、固有値分の特徴量の標準偏差に違いが残る。無相関化+正規化をしたい、というのが白色化のモチベーションとなる。全ての特徴量の標準偏差を1に正規化し、かつ中心化を行う操作を中心化という。
本節では、白色化後の座標系${\bf u}$を定義し、逆算的に白色化操作を説明している。
$${\bf u}=(U_1,\cdots,u_d)^T$$
とした場合、白色化の操作は次のように与えられる。
$${\bf u}={\bf \Lambda}^{-\frac {1}{2}}{\bf S}^T({\bf x}-{\bf μ}) \tag{4.17}$$
${\bf \Lambda}^{-\frac {1}{2}}$は、式(4.14)の各対角要素の平方根をとり更に行列の逆行列を意味する。
ポイントは、これにより${\bf u}$の共分散行列が単位行列にしたいということである。
対角成分の固有値が1に揃い、正規化が行われている。
かつ非対角成分の共分散が全て0なので、無相関化も確認できる。
つまり白色化が行われている。
\begin{pmatrix}
1 & 0 & 0 & \cdots & 0\\
0 & 1 & 0 & \cdots & 0\\
0 & 0 & 1 & \cdots & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \cdots & 1
\end{pmatrix}
続いて、${\bf u}$の共分散行列が単位行列になることを証明する。
まず${\bf u}$の期待値は、
\begin{align}
E[{\bf u}] &={\bf \Lambda}^{- \frac{1}{2}}{\bf S}^T(E[{\bf x}-{\bf μ}])={\bf \Lambda}^{-\frac{1}{2}}{\bf S}^T({\bf μ}-{\bf μ})\\\
&= 0
\end{align} \tag{4.18}
となるので、${\bf u}$の共分散行列は、
\begin{align}
Var[{\bf u}] &= E[{\bf u}{\bf u}^T]=E[{\bf \Lambda}^{- \frac{1}{2}}{\bf S}^T({\bf x}-{\bf μ})({\bf x}-{\bf μ})^T{\bf S}{\bf \Lambda}^{-\frac{T}{2}}]\\\
&= {\bf \Lambda}^{- \frac{1}{2}}{\bf S}^{-1}E[({\bf x}-{\bf μ})({\bf x}-{\bf μ})^T]{\bf S}{\bf \Lambda}^{-\frac{T}{2}}\\\
&= {\bf \Lambda}^{-\frac{1}{2}}{\bf S}^{-1}{\bf \Sigma}{\bf S}{\bf \Lambda}^{-\frac{T}{2}}
\end{align} \tag{4.19}
${\bf \Lambda}^{-\frac{T}{2}}$は${\bf \Lambda}^{- \frac{1}{2}}$の転置行列を表す。
また式(4.19)の最終形の中央部分は${\bf S}^{-1}{\bf \Sigma}{\bf S}$となっているのがわかる。
式(4.14)より${\bf S}^{-1}{\bf \Sigma}{\bf S}={\bf \Lambda}$としているので最終的に、
$$var[{\bf u}]={\bf \Lambda}^{- \frac{1}{2}}{\bf \Lambda}{\bf \Lambda}^{-\frac{T}{2}}={\bf I}$$
とすることができ、${\bf u}$の共分散行列を単位行列にできることが示された。
標準化の場合は、それぞれの特徴の標準偏差に独立に1に正規化されたのに対し、白色化は(回転)と中心化ののち、各軸方向に標準偏差が1に正規化される。したがって、どの方向に対してもデータ分布の標準偏差が単位球上に乗るようになる。
まとめ
-
標準化
・各特徴量の測定単位による影響を取り除く手法。
・線形変換を$z=\frac{x-\mu}{\sigma}$とすることで標準化。
・平均を1・分散を0にすることで実現。 -
無相関化
・特徴間の相関を取り除く手法。
・線形変換を${\bf y}={\bf S}^T{\bf x}$とすると、共分散行列が対角化された形を得られる。
・共分散行列の固有のベクトルを並べた直交行列で、元の共分散行列を対角化することで実現。
・天下り的に定義していることもあり、接続が曖昧な部分が多い。 -
白色化
・標準化も無相関化もする手法。
・白色処理後の座標系に与えられる${\bf u}={\bf \Lambda}^{-\frac {1}{2}}{\bf S}^T({\bf x}-{\bf μ})$によって得られる。
・${\bf u}$の共分散行列を単位行列にすることで実現。
・本書では天下り的に白色化する変換式を与え、それを証明する形の記述をしている。
はじパタ4章 確率モデルと識別関数(前半メモ) 以上

