バックエンドエンジニアがscikit-learn入門しました【教師あり学習編】

はじめに

機械学習ライブラリのデファクトスタンダード的存在であるscikit-learnの「教師あり学習の概要」と「定量的評価手法」についてまとめます。
数学レベルでの理解は途中で挫折したため、まずはライブラリから概要を理解しようと思いまとめました。

教師なし学習編はこちら
前処理編はこちら

教師あり学習とは

教師あり学習とは、入出力のペア(ラベル付きデータ)から学習を行う手法である。
教師あり学習は、回帰と分類の2つの大きなタスクに活用される。
事前にラベル付きデータを用意する必要がある。

予備知識編

回帰や分類、それらの定量的評価の説明の前に、前提となる予備知識を説明しておく。

overfitingとunderfiting

overfiting(過学習)

学習データにfitしすぎてしまうことをoverfitingと呼ぶ。学習データに特化しすぎてしまうためテストデータに対する予測がうまくいかない。
学習データの精度が著しく高く、テストデータの精度との差が大きい場合はoverfitingの可能性が高い。
overfitingを解決するためには、正則化か学習データの数を増やすという解決策がある。学習データにfitしすぎてしまう問題に対して、学習量を増やすというのは一見矛盾しているように感じるかもしれないが、要は学習のバラエティを増やしてAIの視野を広げてあげるイメージ。

underfiting

学習データに対する学習が不十分な状態をunderfitingと呼ぶ。学習データの精度とテストデータの精度がほぼ同じの場合、underfitingの可能性が高い。

スイートスポット

overfitingでもなくunderfitingでもないちょうど良い状態をスイートスポットと呼ぶ。パラメータチューニングが可能なアルゴリズムの場合は、スイートスポットを目指して調整する。

線形モデル

線形モデルは、 w[0]x[0] + w[1]x[1] + ... + w[n]x[n] + b の式を用いる手法である。
「正則化パラメータ(回帰ではalpha、分類ではC)のチューニング」、「L1正則化かL2正則化のどちらを使うか」が大きな性能調整の手段である。
学習も予測も一般的に高速である。

回帰

回帰の線形モデルでは、特徴量の次元数に応じた線形関数で予測を行う。学習により係数wとbを求めていく。

y = w[0]x[0] + w[1]x[1] + ... + w[n]x[n] + b

w[i]とx[i]の組み合わせは次元数に相当する。
例えば、次元数が1つの場合は y = w[0]x[0] + b となり直線の式になる。

本記事で扱う回帰の線形モデルは以下である。

• 最小二乗法
• リッジ回帰
• ラッソ回帰

分類

分類の線形モデルでは、次元数に応じた決定境界(二次元なら直線、三次元なら平面、四次元以上なら超平面)でラベルの分類を行う。学習により係数wとbを求めていく。

2値分類(ラベルが2種類のみ)では、以下の式を用いて、0より大きければラベルA、0より小さければラベルBなどと分類する。

y = w[0]x[0] + w[1]x[1] + ... + w[n]x[n] + b > 0

多値分類(ラベルが3種類以上)では、以下の式を用いて、各ラベル毎に「そのラベルかそうでないか」の値を計算する。つまり、ラベルの数だけ決定境界を用意することになる。そして、yの値が最も大きいラベルを解とする。

y = w[0]x[0] + w[1]x[1] + ... + w[n]x[n] + b

本記事で扱う分類の線形モデルは以下である。

• ロジスティック回帰
• サポートベクターマシン

回帰

回帰は、連続値のデータを予測するタスクである。
本記事では、以下の基本的なアルゴリズムを紹介する。

• k-最近傍法
• 最小二乗法
• リッジ回帰
• ラッソ回帰

k-最近傍法(k-NN)

アルゴリズム概要

以下を満たす単純なアルゴリズムである。

• k=1の場合には、ある時点の回帰の予測値をその時点で最も近い学習データの値とする
• k>1の場合には、ある時点の回帰の予測値をその時点で最も近いk個の学習データの平均値とする

他のアルゴリズムのように学習データを使って何か複雑な計算して学習モデルを生成するのではなく、もはや、学習データそのままあるいは平均値を出力する極めて単純なモデルである。
距離はユークリッド距離を用いるのが一般的である。
パラメータをそれほど調整しなくてもそこそこの精度は出る。
次元数が多い（数百以上）とうまく機能しにくい。
実際にはベースラインくらいにしか使われない。

実行例

# インスタンス化
knr = KNeighborsRegressor(n_neighbors=3)

# 学習
knr.fit(X_train, y_train)

# 予測
knr.predict(X_test)

# 評価
knr.score(X_test, y_test)

主なパラメータ

• n_neighbors : 最近傍点の数（なんで"k_neighbors"じゃないんだろう）

最小二乗法

アルゴリズム概要

回帰直線をy=wx+bとした時(特徴量が1つのみ)に、予測値と学習データの正解値との平均二乗誤差(予測値と正解値の差を二乗したものの平均値)が最小になるようにwとbを計算して学習モデルを生成するアルゴリズムである。
調整できるパラメータが無いため、overfitingしてもパラメータによる調整ができない。
低次元数だとoverfitingになりにくいが、高次元だとoverfitingになりやすい。
後述のリッジ回帰やラッソ回帰のベースとなる手法で、最小二乗法単体で使われることは滅多にない。

実行例

# インスタンス化
lr = LinearRegressor()

# 学習
lr.fit(X_train, y_train)

# 予測
lr.predict(X_test)

# 評価
lr.score(X_test, y_test)

主なパラメータ

• 特になし

リッジ回帰

アルゴリズム概要

最小二乗法にL2正則化を適用し、係数wの要素の値を0に近づけて(傾きを小さくして)モデルを単純化するアルゴリズムである。
単純化とは、イメージとしては、学習データに対してギザギザにきっちり学習していたのをてきとーになめらかな線で学習する感じです。これにより、高次元だと発生しやすい最小二乗法のoverfitingの問題を解決できる。
wの値が小さくなると、汎化してモデルが簡潔になることを意味するので学習データに対する性能は落ちる。ただし、我々が欲しいのはテストデータに対する性能である。

学習データ数が多くなれば最小二乗法のoverfitingの問題は解決され、両者はそれほど精度が変わらなくなってくる。

実行例

# インスタンス化
r = Ridge(alpha=0.1)

# 学習
r.fit(X_train, y_train)

# 予測
r.predict(X_test)

# 評価
lr.score(X_test, y_test)

主なパラメータ

• alpha : 係数wの要素の値をどれだけ小さくするかのパラメータ。alphaを大きくすると係数wの値は小さくなる。最良の値はデータセットに依存するためチューニングが必要。デフォルト値は1.0。

ラッソ回帰

アルゴリズム概要

最小二乗法にL1正則化を適用し、係数wの要素の値を0に近づけてモデルを単純化するアルゴリズムである。
リッジ回帰のL2正則化との違いは、L1正則化は係数wのうちいくつかを0にして、アルゴリズムが重要でないと判断した特徴量を無視する点である。L2正則化では0に近づけたとしても0にはしない。そういった意味で、L1正則化はL2正則化よりも極端である。
データ中に重要そうな特徴量はあきらかに少ないなと思うときに使うと良い。とりあえずはリッジ回帰を使って、ゴミ特徴量が多そうであればラッソ回帰を使ってみるのがよい。

実行例

# インスタンス化
l = Lasso(alpha=0.1)

# 学習
l.fit(X_train, y_train)

# 予測
l.predict(X_test)

# 評価
l.score(X_test, y_test)

主なパラメータ

• alpha : 係数wの要素の値をどれだけ小さくするかのパラメータ。alphaを大きくすると係数wの値は小さくなる。最良の値はデータセットに依存するためチューニングが必要。デフォルト値は1.0。

分類

分類は、対象データのラベルを推定するタスクである。
本記事では、以下の基本的なアルゴリズムを紹介する。

• k-最近傍法
• ロジスティック回帰
• ナイーブベイズ分類器
• 決定木
• ランダムフォレスト
• 勾配ブースティング決定木
• サポートベクターマシン
• ニューラルネットワーク

また、「k-最近傍法」、「決定木」、「ランダムフォレスト」、「勾配ブースティング決定木」、「サポートベクターマシン」、「ニューラルネットワーク」は分類でも回帰でもどちらのタスクでも適用できる。

k-最近傍法(k-NN)

アルゴリズム概要

以下を満たす単純なアルゴリズムである。

• k=1の場合には、最近傍点(最も近い点)のラベルを対象テストデータのラベルとする
• k>1の場合には、k個の最近傍点のうち最も多いラベルをそのテストデータのラベルとする

距離はユークリッド距離を用いるのが一般的である。
実際には、ベースラインくらいにしか使われない。

実行例

# インスタンス化
knc = KNeighborsClassifier(n_neighbors=3)

# 学習
knc.fit(X_train, y_train)

# 予測
knc.predict(X_test)

# 評価
knc.score(X_test, y_test)

主なパラメータ

• n_neighbors : 最近傍点の数。3~5くらいでうまくいくことが多い。

ロジスティック回帰

アルゴリズム概要

導出関数にシグモイド関数を用いて最尤推定法でパラメータを決定する線形モデルのアルゴリズムである。
名前に"回帰"とありつつも実は分類器であることに注意。
高次元データの場合に強力である。

実行例

# インスタンス化
lr = LogisticRegression(C=10, penalty="l1")

# 学習
lr.fit(X_train, y_train)

# 予測
lr.predict(X_test)

# 評価
lr.score(X_test, y_test)

主なパラメータ

• C : 正則化パラメータ。回帰のalphaと逆で、Cの値が小さいとwを0に近づけることでモデルを単純にする。デフォルト値は1.0。
• penalty : L1正則化を使うかL2正則化を使うか。L1は極端なのでとりあえずはL2を使ってみるのが良い。デフォルトはL2。

ナイーブベイズ分類器

アルゴリズム概要

ベイズの定理を利用した同時確率の積の大小比較による分類を行うアルゴリズムである。
scikit-learnにはGaussianとMultinomialとBernoulliの3種類のナイーブベイズ分類器が実装されている。
高次元データではGaussianが有利である。
スパースでない大量データの場合はMultinomialの方が有利だが、それ以外ではBernoulliの方が有利である。
精度は悪くはない。スパースなデータにもそれなりの精度をだす。
学習も予測も高速である。
ベースラインとしてよく使われる。

実行例

# インスタンス化
mnb = MultinomialNB()
bnb = BernoulliNB()

# 学習
mnb.fit(X_train, y_train)
bnb.fit(X_train, y_train)

# 予測
mnb.predict(X_test)
bnb.predict(X_test)

# 評価
mnb.score(X_test, y_test)
bnb.score(X_test, y_test)

主なパラメータ

• alpha : モデルの複雑さを制御する。値が大きくなるとモデルは単純になる。

決定木

アルゴリズム概要

特徴量空間上で学習データをラベルごとに分割できるような直線で分割する。これらを再帰的に繰り返し、特徴量空間上で学習データを細分化する分割領域が形成される。各分割領域は決定木の終端ノードに相当する。
予測では、特徴量空間上でテストデータが存在する分割領域内で、最も多い学習データのラベルが解となる。

アルゴリズム自身が「重要度が高い特徴量」を自動選択する。どの特徴量を重要視したかもグラフで可視化して確認できる。また、分割領域の閾値も自動決定する。
学習結果が木なので可視化することで理解が容易である。

終端ノードが同じラベルのデータのみで構成されるようになるまで学習を繰り返すのは一見良いように見えるが、それはoverfitingに陥る可能性が高いため、事前枝刈り(木の深さや葉の数を制限するなど)を行う必要がある。事前枝刈りを行うことで、ノード内にはラベルが異なるデータは混在するもののいずれかのクラスに偏った状態になりやすくなる。
しかしながら、事前枝刈りを行ったとしてもoverfitingに陥ることも多々ある。したがって、決定木単体で使用されることは少なく、後述するランダムフォレストや勾配ブースティング決定木などでアンサンブル（複数の機械学習を組み合わせたもの）として利用されるパターンが多い。

実行例

# インスタンス化
dtc = DecisionTreeClassifier(max_depth=4)

# 学習
dtc.fit(X_train, y_train)

# 予測
dtc.predict(X_test)

# 評価
dtc.score(X_test, y_test)

主なパラメータ

• max_depth : 事前枝刈りパラメータ。木の最大深さ。
• max_leaf_nodes : 事前枝刈りパラメータ。ノードの最大数。
• min_samples_leaf : 事前枝刈りパラメータ。分割領域でのデータの最小数。

ランダムフォレスト

アルゴリズム概要

少しずつ異なる複数の決定木を用意し、それぞれの決定木の予測結果の平均を取るアルゴリズムである。平均を計算することで、たとえ1つ1つの決定木がoverfitingしていたとしても、その問題を解消する。
各決定木の構築時(学習データの選択と特徴量の選択)に乱数を適用することで、複数の異なる決定木を構築する。ゆえに、"ランダム"フォレストという名前になっている。
決定木では個々のノードで最適なテストを作成するために、最も重要度が高い特徴量を選択していたが、ランダムフォレストでは特徴量は乱数により選択される。
分類予測時は、各決定木がそれぞれのラベルごとに確率値を算出し、全ての決定木での確率値の平均値が最も高いものを解とする。

分類では最もポピュラーな手法の1つ。
精度は高く、パラメータチューニングもそれほど多くなく、スケール変換も不要である
スパースデータにはあまり向いていない。
学習も予測も時間がかかる。

実行例

# インスタンス化
rfc = RandomForestClassifier(n_estimaters=100, max_depth=4)

# 学習
rfc.fit(X_train, y_train)

# 予測
rfc.predict(X_test)

# 評価
rfc.score(X_test, y_test)

主なパラメータ

• n_estimators : 決定木の数。時間とメモリの許す範囲でなるべく大きくするとよりoverfitingを回避できるので良い。
• max_features : 特徴量選択の候補の数。値を大きくすると決定木と似たような結果になり、小さくすると各決定木は相互に異なるものになるが適合するために深さが必要となる。デフォルト値でうまくいくことが多い。
• max_depth : 事前枝刈りパラメータ。木の最大深さ。
• max_leaf_nodes : 事前枝刈りパラメータ。ノードの最大数。
• min_samples_leaf : 事前枝刈りパラメータ。分割領域でのデータの最小数。
• n_jobs：計算で使用するCPUコア数。-1を指定すると全てのコアを使う。

勾配ブースティング決定木

アルゴリズム概要

1つ前の決定木の誤りを次の決定木が修正して決定木を順に作成していくアルゴリズムである。
アンサンブルである。
乱数を使うのではなく、木の深さを1~5くらいとすることで強力な事前枝刈りを行いoverfitingを回避する。
パラメータチューニング難しいけどうまくいけば、ランダムフォレストよりも良い精度をだす(一般的に機械学習で最も精度高い)。
まずはランダムフォレストからやって、その後少しだけでも精度をあげたいってなったら勾配ブースティング決定木でパラメータチューニング頑張る感じ。
ランダムフォレスト同様、スパースデータにはあまり向いていない。

実行例

# インスタンス化
gbc = GradientBoostingClassifier(n_estimaters=100, max_depth=4)

# 学習
gbc.fit(X_train, y_train)

# 予測
gbc.predict(X_test)

# 評価
gbc.score(X_test, y_test)

主なパラメータ

• n_estimators : 決定木の数。勾配ブースティングの場合は大きすぎるとoverfitingに陥ってしまう。
• learning_rate : 各決定木がそれまでの決定木の過ちをどれくらい補正するかの学習率。値が大きいと強く補正しようとしてモデルは複雑になる。デフォルトでは0.1。
• max_depth : 事前枝刈りパラメータ。木の最大深さ。デフォルトでは3。
• max_leaf_nodes : 事前枝刈りパラメータ。ノードの最大数。
• min_samples_leaf : 事前枝刈りパラメータ。分割領域でのデータの最小数。

サポートベクターマシン(SVM)

アルゴリズム概要

学習により獲得した「サポートベクタ(境界線付近に存在するベクタ)と各テストデータの距離」および「各サポートベクタの重要性」によって分類を行うアルゴリズムである。
SVMのような線形モデルでは、非線形な特徴量を加えることで正確にデータを分類できる。ただし、特徴量が多すぎると計算量が膨大になってしまう。そこで、非線形特徴量が加えられた空間上で2点間の距離を実際に拡張計算せずに算出する方法としてカーネルトリックが存在する。カーネルトリックとしては、多項式カーネルとガウンシアンカーネルがある。
ガウンシアンカーネルであれば、x1とx2間の距離は以下の式で算出される。γはガウシアンカーネルの幅で、||x1-x2||^2はユークリッド距離である。

exp(-γ||x1-x2||^2)

そのままでは各特徴量の大きさが大きく異なるため、全ての特徴量が0から1になるようにスケール変換する必要がある。加えて、パラメータチューニングが難しい。
良い点としては、精度は高い、最もポピュラーな手法の1つである、スパースデータでもうまく機能する、高次元データの場合には強力である、といったことがある。

実行例

# インスタンス化
svc = SVC(kernel='rbf', C=10, gamma=0.1)

# 学習
svc.fit(X_train, y_train)

# 予測
svc.predict(X_test)

# 評価
svc.score(X_test, y_test)

主なパラメータ

• kernel : カーネルの種類。RBFなど。
• gamma : ガウシアンカーネルの幅。値が小さいとカーネルの直径が大きくなり多くの点を近いと判断するため単純なモデルになり、大きくなると個々のデータにfitingする。デフォルトは"1/特徴ベクトル次元数"。
• C : 正則化パラメータ。デフォルトは1。

ニューラルネットワーク(多層パーセプトロン)

アルゴリズム概要

入力層と隠れ層と出力層の3層から成り、次の層のベクトルは、前の層のベクトルと重みの積和に非線形活性化関数(relやtanh)を適用したものになる。
重みは学習により獲得される。初期値は乱数で与えられる。
パラメータ調整が難しくスケール変換が必要だが精度は高い。

scikit-learnではニューラルネットワークの一部機能しか実装しておらず、GPU対応もしていないため、ニューラルネットワーク(ディープラーニング)を実装するのであれば他ライブラリ(Tensorflowなど)を使うべし。

実行例

# インスタンス化
mlpc = MLPClassifier(solver='lbfgs', activation='tanh', hidden_layer_sizes=[20,10], alpha=0.1)

# 学習
mlpc.fit(X_train, y_train)

# 予測
mlpc.predict(X_test)

# 評価
mlpc.score(X_test, y_test)

主なパラメータ

• solver : モデルを学習するアルゴリズムの種類。デフォルトの"adam"はデータスケールが適切に調整されていればよく機能する。"lbfgs"はadamほどデータスケールに敏感ではないがデータセットが大きいと学習に時間がより多くかかる。"sgd"は多くの設定パラメータが存在し、上級者向けだがうまく調整できれば精度は高い。
• activation : 非線形活性化関数の種類。デフォルトはrelu。
• hidden_layer_sizes : 隠れ層のユニット数と層数。[隠れ層1のユニット数, 隠れ層2のユニット数, ....]と定義する。デフォルトは100ユニット1層。
• alpha : l2正則化パラメータ
• max_iter : 学習繰り返しの回数。adamアルゴリズムの場合のみ指定できる。

定量的評価

評価値

score関数

回帰のタスクではR2乗値を算出するのに使用する。

分類のタスクではscore関数ではなく後述するF値を使用する。
なぜならば、score関数は分類では精度しか算出しないからである。
精度だけでは、クラスが偏ったデータセットの場合は適切な評価をすることができない。例えば2値分類で、一方のクラスAのデータが90％、もう一方のクラスBが10パーセントで構成されたデータの場合、分類器が常にAと判定してしまう誤ったものであったとしても、その分類器の性能は90％と高い値をだしてしまう。これでは正しい評価ができているとは言えない。

F値

F値は適合率と再現率から算出される、データセット内のクラスの偏りに依存しない分類の評価指標である。
適合率と再現率はトレードオフの関係にある。

混同行列(Confusion Matrix)

混同行列とはこちらにあるような表です。

• TP(True Positive)：Positiveと判定したもののうち本当にPositiveだった個数(正解)
• FP(False Positive)：Positiveと判定したもののうち本当はNegativeだった個数(誤り)
• FN(False Negative)：Negativeと判定したもののうち本当はPositiveだった個数(誤り)
• TN(True Negative)：Negativeと判定したもののうち本当にNegativeだった個数(正解)

適合率（Precision）

判定結果の精度を示す指標である。
Positiveと判定したもののうち本当にPositiveである割合。(あるいはNegative)

Precision = \frac{TP}{TP+FP}

再現率（Recall）

いかに漏れなく拾えているかを示す指標である。
全てのPositiveであるもののうち、Positiveと判定されたものの割合。(あるいはNegative)

Recall = \frac{TP}{TP+FN}

F値

重み付きF値

重みパラメータを用いたF値。

WeightedF = \frac{(1+\beta)^2 \times Precision \times Recall}{\beta^2 \times Precision+Recall}

F1値

重みパラメータの値が1のF値。調和平均となる。
F値といえば一般的にこれを指す場合が多い。

F1 = \frac{2 \times Precision \times Recall}{Precision+Recall}

実行例

# 適当に分類のインスタンス生成
lr = LogisticRegression()

# 学習データに適合
lr.fit(X_train, y_train)

# F1値でスコア算出
f1_score(y_test, lr.predict(X_test))

# 適合率、再現率、F値をまとめて出力。target_namesの値は任意の文字列。
print(classification_report(y_test, lr.predict(), target_names=["Positive", "Negative"]))

交差検証(クロスバリデーション)

分割交差検証

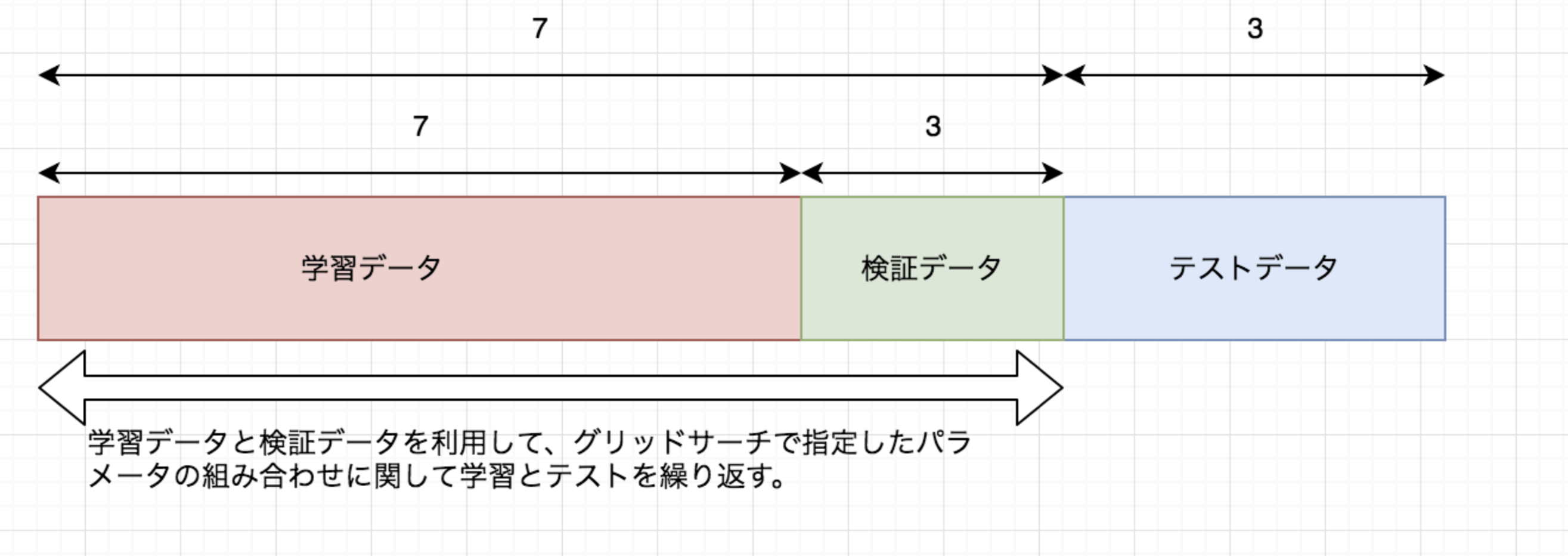
分割交差検証は、データを「学習データ」と「検証用データ」と「テストデータ」の3つに分割し、学習データと検証用データの組み合わせを少しずつ変更しながら複数回学習とテストの組み合わせを実施し、評価の精度を高める手法である。
本記事では、以下を説明する。

• k分割交差検証
• 層化k分割交差検証

k分割交差検証

任意のk個にデータを分割して、k-1個を学習データ、1個を検証用データとする。それらのデータを入れ替えながらk回の交差検証を繰り返して出た値の平均値をスコアとすることで、単純に学習データとテストデータに分割しただけの評価よりも回数が多い分、信頼度の高いスコアを得ることができる手法である。
交差検証の中で最もシンプルな手法である。
難点として、k回学習とテストを行うので実行時間がかかることがあげられるが、評価は少しくらい遅くても問題ない。
scikit-learnでは回帰のデフォルト手法である。

層化k分割交差検証

各分割内でのクラスの比率がデータ全体の比率と同じになるように分割して交差検証する手法である。
k分割交差検証はデータの先頭から1/kずつ分割していくが、例えばデータセットの並び順がクラス順になっていた場合は偏った分割データになってしまうため、適切な分類の学習とテストができない。それを解消してくれる。
scikit-learnでは分類のデフォルト手法である。

実行例

# 回帰モデルのインスタンス生成
r = Ridge()

# 分類モデルのインスタンス生成
lr = LogisticRegression()

# 回帰モデルはk分割交差検証で評価
# mean()は配列の平均値を計算する
cross_val_score(r, data, target, cv=5).mean()

# 分類モデルは層化k分割交差検証で評価
cross_val_score(lr, data, target, cv=5).mean()

主なパラメータ

• 第一引数: 機械学習モデルのインスタンス
• 第二引数: データ（学習用やテスト用にスプリットしていないもの）
• 第三引数: 正解ラベル（学習用やテスト用にスプリットしていないもの）
• cv: 分割する任意のk個の値。デフォルトは3。また、交差検証分割器をcvに与えることでより複雑な分割制御を行える。

シャッフル交差検証

データのうち任意のサイズの「学習データ」と「学習データと重複しないテストデータ」による評価を繰り返す手法である。

実行例

# 機械学習モデルインスタンス生成
lr = LogisticRegression()

# シャッフル交差検証のインスタンス生成
ss = ShuffleSplit(test_size=.7, train_size=.3, n_splits=10)

# 交差検証実行
cross_val_score(lr, data, target, cv=ss).mean()

パラメータ

• train_size: 学習データの数または割合。整数で個数、浮動小数点で割合を指定できる。
• test_size: テストデータの数または割合。整数で個数、浮動小数点で割合を指定できる。
• n_splits: 分割数

その他交差検証

1つ抜き交差検証、グループ付き交差検証などさまざまなユースケースに対応するための分割方法が存在し、scikit-learnで実装されている。ここではまとめない。

グリッドサーチ

グリッドサーチとは、指定したパラメータの組み合わせを全通り試してもっとも良い組み合わせを導き出す手法である。グリッドサーチにより精度の向上が期待できる。
グリッドサーチでは学習データとテストデータの他に「検証データ」と呼ばれるスコア比較用のデータを用意する必要がある。テストデータをスコア比較には使用しないようにするためである。
学習とテストの比率は7:3の黄金比。

実行例

forループでグリッドサーチする例：

# 初期化
best_score = 0
best_gamma = 0
best_C = 0

# グリッドサーチ
for g in [0.1, 1, 10]:
   for c in [0.1, 1, 10]:
      # インスタンス生成
      svm = SVC(gammma=g, C=c)
      # 学習データで学習
      svm.fit(X_train, Y_train)
      # 検証データで比較用のスコア計算
      score = svm.score(X_verification, y_verification)
      # いままででベストならばスコアとパラメータ値を更新
      if score > best_score:
         best_score = score
         best_gamma = g
         best_C = c

# グリッドサーチで最適なパラメータが分かったのでそのパラメータでモデルの作り直し
svm = SVC(gamma=best_gamma, C=best_C)

# 学習データ＋検証データで学習（今度は検証データも学習する）
svm.fit(X_train_verification, y_train_verification)

# テストデータで最終的なスコア算出
svm.score(X_test, y_test)

交差検証+グリッドサーチ

交差検証とグリッドサーチを組み合わせて、指定した全てのパラメータの組み合わせ毎に交差検証を行う手法がある。
グリッドサーチ単体では学習データと検証データの分割が1回だけしか実行されないため、その分割のされ方に依存して性能が変動がする可能性がある。
グリッドサーチをしながら交差検証を実施するため、検証データを別途用意する必要はない。（当然ながら、学習データとテストデータを用意する必要あり。）
交差検証とグリッドサーチの組み合わせはよく用いられ、そもそも「交差検証+グリッドサーチ」を「交差検証」と呼ぶ場合もある。
交差検証とグリッドサーチを同時に行うため実行時間がかかる。
最初から細かい間隔でたくさんのパラメータでグリッドサーチするよりも、最初は間隔広めで徐々に狭めていてくのが良い。

実行例

forループ実装の例：

best_score = 0
best_gamma = 0
best_C = 0

# グリッドサーチ
for g in [0.1, 1, 10]:
   for c in [0.1, 1, 10]:
      # インスタンス生成
      svm = SVC(gammma=g, C=c)
      # 交差検証
      score = cross_val_score(svm, X_train, y_train, cv=5).mean()
      if score > best_score:
         best_score = score
         best_gamma = g
         best_C = c

# グリッドサーチ+交差検証で最適なパラメータが分かったのでそのパラメータでモデルの作り直し
svm = SVC(gamma=best_gamma, C=best_C)

# 学習データ＋検証データで学習
svm.fit(X_train, y_train)

# 評価
svm.score(X_test, y_test)

GridSearchCVクラスを利用した例：

from sklearn import svm
from sklearn.model_selection import GridSearchCV

# 分類機
clf = svm.SVC()

# パラメータ
param = [
        {'C': [1, 10, 100, 1000], 'kernel': ['linear']},
        {'C': [1, 10, 100, 1000], 'kernel': ['rbf'], 'gamma': [0.001, 0.0001]},
        {'C': [1, 10, 100, 1000], 'kernel': ['poly'], 'degree': [2, 3, 4], 'gamma': [0.001, 0.0001]},
        {'C': [1, 10, 100, 1000], 'kernel': ['sigmoid'], 'gamma': [0.001, 0.0001]}

# GridSearchCVクラスでインスタンス生成
gs = GridSearchCV(clf, param, cv=5, scoring='f1')

# グリッドサーチ+交差検証
gs.fit(X_train, y_train)

# テストデータでスコア算出
gs.score(X_test, y_test)

# グリッドサーチ+交差検証の結果を出力
print(gs.cv_results_)

# ベストのパラメータの組み合わせを出力
gs.best_estimator_

↑forループの方が直感的でわかりやすいが、GridSearchCVクラスを利用すればすっきりとしたコードになる。

不確実性推定の閾値

scikit-learnの分類器には不確実性推定機能(単にクラスを判定するだけでなくどれくらいの確実性を持った判定なのかを示す機能)がdecision_function関数あるいはpredict_proba関数として実装されている。ほとんどのクラス分類器は両方が実装されており、少なくともどちらかは実装されている。
分類の予測時には、実際にはdecision_function関数やpredict_proba関数の出力が固定の閾値で判定されているのである。デフォルトの閾値はdecision_function関数の場合は0、predict_proba関数の場合は0.5である。この閾値を調整することで適合率と再現率のトレードオフを調整し、最適な分類を行うことができる。

precision-recall(適合率-再現率)カーブ

precision-recallカーブとはすべての可能な閾値に対するprecisionとrecallの値の組み合わせをグラフにしたものである。
下にprecision-recallカーブのイメージ図を描いてみました。

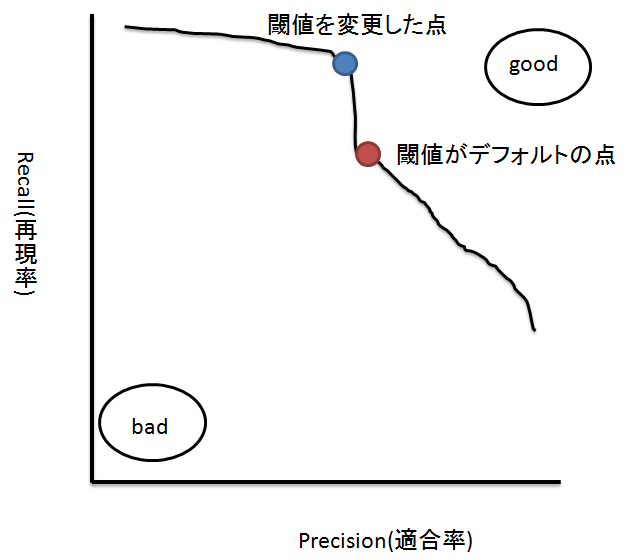
グラフの右上にいくほどF値の値は良くて左下にいくほど悪い。この図の場合、赤点をデフォルトの閾値とすると、閾値を青点に変更することでより良いF値が得られる。
このように、f1_score関数で得られたF値は単なるデフォルトで与えられた閾値でのスコアにすぎないため、カーブを描いてみることでより適切な箇所を見つけられる可能性がある。
precision-recallカーブはscikit-learnのprecision_recall_curve関数とmatplotにより簡単に描画できる。

複数の機械学習モデルをprecision-recallカーブで描画して比較する場合、人間の目には微妙で判断しずらい場合がある。その場合は、カーブ下の面積（平均適合率）を積分により取得して、その面積が大きいモデルを採用すればよい。

# 適当な機械学習モデルの用意
rf = RandmForestClassifier()
rf.fit(X_train, y_train)

# 平均適合率の計算
average_precision_score(y_test, rf.predict(X_test))

受信者動作特性(ROC)カーブ

ROCカーブとは、precision-recallカーブの適合率と再現率がそれぞれ真陽性率(TPR:True Positive Rate)と偽陽性率(FPR:False Positive Rate)になったものである。
precision-recallカーブと同様にroc_curveとmatplotによるグラフ描画が可能で、面積比較のためのroc_auc_scoreという関数が用意されている。
真陽性率は再現率と同じだが、偽陽性率は全てのNegativeデータの個数に対するFalse Positiveの割合である。

FPR = \frac{FP}{FP+TN}

教師あり学習に関する俺的（初心者的）まとめ

• 回帰はリッジ回帰が最強説
• 分類はスパースデータでなければランダムフォレスト、スパースデータであればサポートベクタマシンが最強説
• でも他にもいろいろ要因はあるから何が最強かは結局のところ、ケースバイケース。
• アルゴリズムは回帰と分類の両方に利用できるものもあるし、片方にしか利用できないものもある。
• 教師あり学習は定量的評価ができる。
• 定量的評価のためにはテストデータが必要。
• とりあえず教師あり学習の評価をする時は交差検証とグリッドサーチを組み合わせる。
• とりあえず分類の評価はf1_score関数使う。
• とりあえず回帰はscore関数使う。

参考

Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎