TL;DR
- 円周率の近似計算の手法を比較した
- 効率的なアルゴリズムについて考察した
はじめに
本記事は、芝浦工業大学 工学部サマースクーリング(情報・通信工学課程)に参加した経験を再構成し、作成したものです。内容の大半は、私自身の調査・研究によって明らかにしたものですが、一部において、TAや教員の方々にサポートしていただいた部分があります。この場を借りて、ご協力をいただいた方々に感謝申し上げます。
また、本記事の公開において問題がございましたら、早急に対応しますので、コメント機能もしくはwisteriatp@gmail.comまでご連絡をお願いいたします。
おことわり
筆者は数学やプログラミングに関する知識が十分ではないため、本文に誤りが含まれている可能性があります。ご指摘、アドバイス等いただけますと幸いです。
1. 目的
より高精度な近似計算をするために、効率的なアルゴリズムについて考察したい。そのために効率的なアルゴリズムとは何かを定義することを目的とする。
2. 前提
2.1. 意義
円周率を高精度に近似計算する意義は以下の通りである。
- スケールの大きい分野で利用
- ex. 建築, 土木, 宇宙開発
- コンピュータの性能向上
- CPUやRAM・ROMの性能が重要
- ベンチマークにも用いられる
- アルゴリズムの研究開発
- 近似計算に用いられるアルゴリズムは、円周率以外の分野(ex. 統計, 金融, 物理)でも活用される
ただし、実用的には小数第15位程度の値が用いられるようである。
2.2. 歴史
13世紀まで ―幾何学―
紀元前3世紀のアルキメデスの方法など、円に内接・外接する多角形用いて近似する手法が用いられた。
14世紀~20世紀前半 ―解析―
1674年のライプニッツの公式など、級数が発見された。
20世紀後半~現在
1989年のチュドノフスキーの公式など、計算機による計算が一般的に行われるようになった。
2024年9月現在の世界記録
アメリカのハードウェア企業であるStorageReview Labが2024年6月28日に発表した「202,112,290,000,000 桁」が最高記録とされる。
2.3. 必要な知識
本記事では、三角関数, 数列, 極限などの高校数学の知識を用いる。
3. 課題設定
1. 目的で設定したように、近似計算には効率的なアルゴリズムが必要である。
ここでは、効率的なアルゴリズムをより早く近似できる手法と定義し、それを評価する方法について検討する。
3.1. 仮説
Ⓐ試行ごとの計算量とⒷ真値に近づくまでの早さを利用できると考え、これらについて検証することとする。
4. 比較方法
3.1. 仮説の通り、Ⓐ試行ごとの計算量・Ⓑ真値に近づくまでの早さの2点について検討する。
4.1. 具体的な方法
Ⓐ試行ごとの計算量
式とフローチャートから計算量を求める。
Ⓑ真値に近づくまでの早さ
$\pi$に近づくまでの試行回数・計算時間を計測する。
具体的には、アルゴリズムは試行を繰り返すごとに精度が向上することを前提に、以下の条件を満たすまで試行を繰り返し、実行開始からの値の変化と計算時間を記録する。
- 移動量が「0.0003未満」(誤差が約0.01%未満)である
- 値が「3.141‥」である
- 後述する一部のアルゴリズムで発生する予測不能な挙動を抑えるため
4.2. 真度の検証
真度とは真値との一致の程度のことである。
今回は、円周率が既知のものであるとして検証を行うが、実際のアルゴリズムは未知の円周率を求めるために使われる。その際に、求めた近似値が正しいかを評価する方法について調べた。一般的にとられる手法は以下のようである。
-
下限値<X<上限値を示す- アルキメデスの手法など
- 他の手法で求めた値と比較する
- BBP公式(≒$\pi$の特定の桁を求める手法)と比較する
- 先述した世界記録ではこれが用いられたそう
4.3. 検証環境
Python3で以下のようなコードを作成し、Google Colaboratoryの無料プラン上で実行した。
5. 結果
以下の7つに手法に対して、検証を行った。
| 番号 | 手法 | 説明・式 |
|---|---|---|
| ㋑ | 内接多角形の外周の長さ | $\lim_{n \to \infty} \frac{n}{2} \sqrt{2 - 2\cos(\frac{2\pi}{n})}$ |
| ㋺ | 外接多角形の外周の長さ | $\lim_{n \to \infty} n\tan\frac{\pi}{n}$ |
| ㋩ | モンテカルロ法 | ランダムな座標が円の内部に含まれるかを調べる |
| ㋥ | ライプニッツの公式 | $\frac{\pi}{4} = \sum_{n=0}^\infty \frac{(-1)^n}{2n+1}$ |
| ㋭ | チュドノフスキーの公式 | $\frac{1}{\pi} = 12 \sum_{n=0}^\infty \frac{(-1)^n \cdot (6n)!}{(3n)! \cdot (n!)^3} \cdot \frac{13591409 + 545140134n}{640320^{3n + \frac{3}{2}}}$ |
| ㋬ | 区分求積法 | $4 \lim_{n\to \infty} \sum_{k=1}^{n} (\frac{1}{n} \sqrt{1-(\frac{2k-1}{2n})^2})$ |
| ㋣ | 二分法 | $\tan x = 1$を用いて$\pi$を含む範囲を絞り込む |
以下がその結果である。
Ⓐ試行ごとの計算量
| 番号 | 手法 | 計算量 |
|---|---|---|
| ㋑ | 内接多角形の外周の長さ | $O(1)$ |
| ㋺ | 外接多角形の外周の長さ | $O(1)$ |
| ㋩ | モンテカルロ法 | $O(n)$ |
| ㋥ | ライプニッツの公式 | $O(n)$ |
| ㋭ | チュドノフスキーの公式 | $O(n)$ |
| ㋬ | 区分求積法 | $O(n^2)$ |
| ㋣ | 二分法 | $O(n)$ |
Ⓑ真値に近づくまでの早さ
試行ごとの値をグラフにすることで比較する。
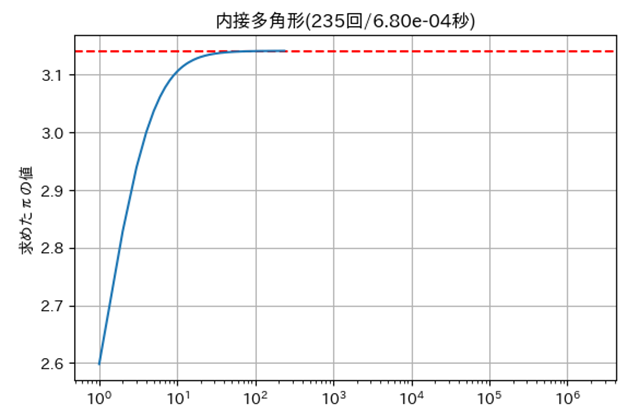
㋑内接多角形の外周の長さ
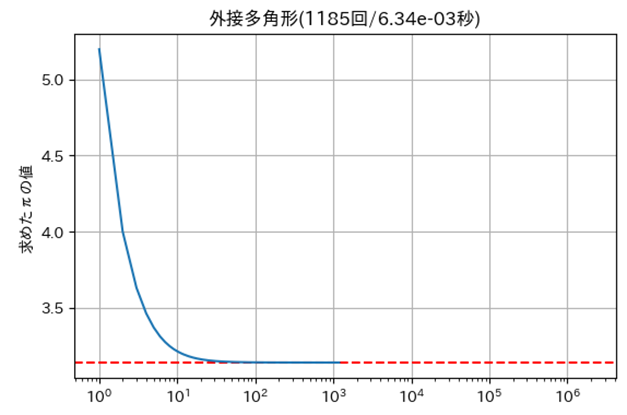
㋺外接多角形の外周の長さ
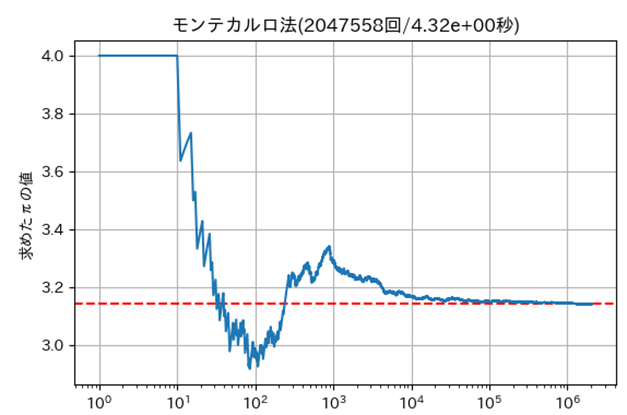
㋩モンテカルロ法
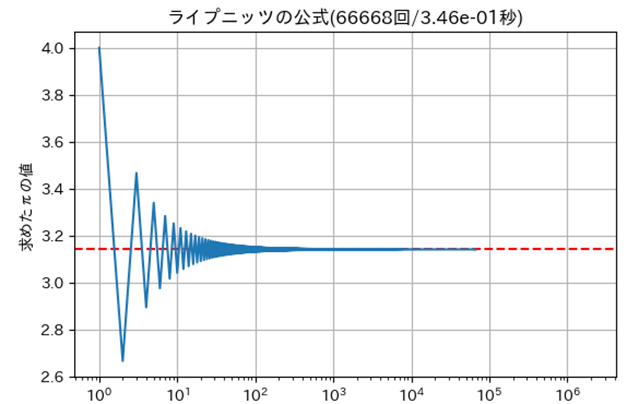
㋥ライプニッツの公式
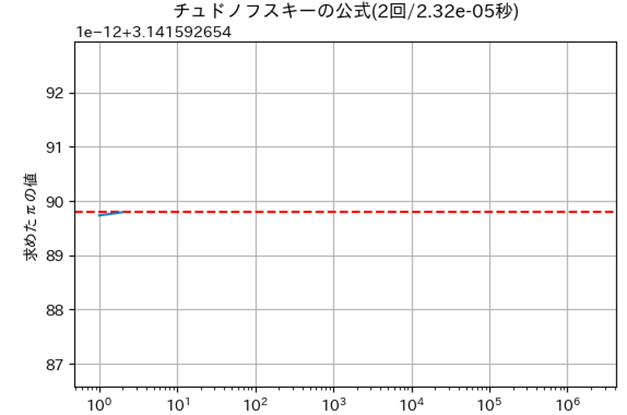
㋭チュドノフスキーの公式
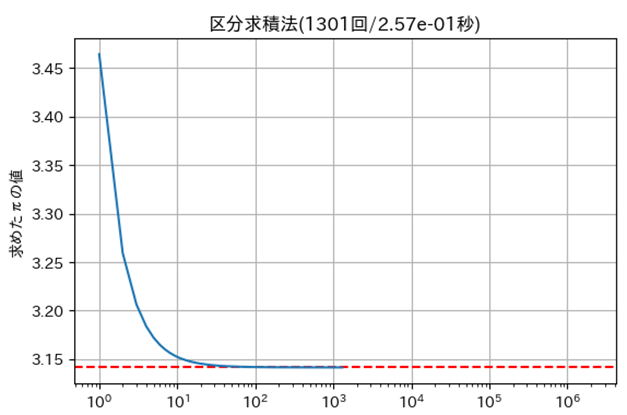
㋬区分求積法
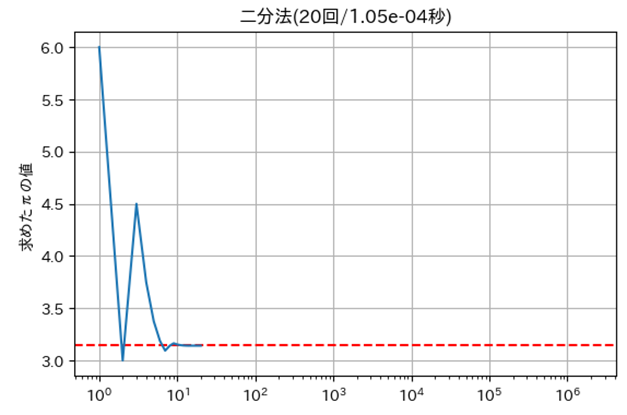
㋣二分法
まとめ
| 番号 | 手法 | 試行回数(回) | 実行時間(秒) |
|---|---|---|---|
| ㋑ | 内接多角形の外周の長さ | $235$ | $6.80 \times 10^{-4}$ |
| ㋺ | 外接多角形の外周の長さ | $1{,}185$ | $1.71 \times 10^{-4}$ |
| ㋩ | モンテカルロ法 | 検証不可1 | 検証不可1 |
| ㋥ | ライプニッツの公式 | $66{,}668$ | $3.46 \times 10^{-1}$ |
| ㋭ | チュドノフスキーの公式 | $2$ | $2.32 \times 10^{-5}$ |
| ㋬ | 区分求積法 | $1{,}301$ | $2.57 \times 10^{-1}$ |
| ㋣ | 二分法 | $20$ | $1.05 \times 10^{-4}$ |
6. 考察
アルゴリズムの効率性について、以下の2点のことが分かった。
- Ⓐ試行ごとの計算量からはほぼ測ることができない
- Ⓑ真値に近づくまでの早さから測ることができる
しかし、今回の結果では、古くから使われてきた円に内接・外接する多角形の外周の長さを用いた手法が比較的優れた結果となったことから、適切な結果であるといえるかは疑問である。また、この原因として4.1. 具体的な方法で設定した真値に近づくの定義が適切でない可能性があると考えられる。
7. 今後の課題
- アルゴリズムの評価方法について再検討したい
-
真値に近づくまでの早さの検討方法を改善したい
- 収束速度の概念の導入など
- モンテカルロ法など実行結果の推測が不可能なアルゴリズムの評価方法を考えたい
- 条件が異なるアルゴリズムの比較方法を工夫したい
- 例えば幾何学を用いた方法と解析を用いた方法では条件が異なる
- 円周率以外の近似値を求めたい
参考文献
- NASAでは円周率を何桁まで使っているのか? - GIGAZINE
- 【探究・知識を深める】円周率の桁数にみる人類の科学の歩み - ブリタニカ・ジャパン
- StorageReview Lab が 202 兆桁を超える円周率計算の世界記録を更新 - StorageReview.com
- y-cruncher - A Multi-Threaded Pi Program
- 円周率πを内接(外接)する正多角形から求める|yoshik-y
- Chudnovskyの円周率公式の証明 | Mathlog
- 二分法とは? アルゴリズム・収束・例題 - 理数アラカルト -