概要
Artificial Bee Colony 法の初期版でベンチマーク関数の一番簡単なshpere関数で最適値を求めてみましたが、今度はそれよりもさらに性能をアップさせたGbest ABC法を実装してみて、どんな感じで収束するのか見てみました。
アルゴリズムがだいたい似ているので、異なっている部分のみ詳細に記載します。
前回のはこちら。
http://qiita.com/gitkobaya/items/3067273bbd02616c287e
Gbest ABC法
ステップ2とステップ3が異なっています。
##ステップ1 初期化
初期集団をランダムに発生させて、最良点を保持します。
##ステップ2 Employ Bee
以下の式により探索を実施します。
\begin{align}
v^{g}_{ij} &= x^{g}_{ij} + \phi^{g}_{ij}(x^{g}_{ij} - x^{g}_{mj})+\psi^{g}_{ij}(x^{g}_{ij} - x^{g}_{bestj}) \\
x^{g}_{ij} &=
\begin{cases}
v^{g}_{ij} & f_{i}(v^{g}_{i}) \leq f_{i}(x^{g}_{i}) \\
x^{g}_{i} & \text{それ以外}
\end{cases} \\
C_{i} &=
\begin{cases}
0 & f_{i}(v^{g}_{i}) \leq f_{i}(x^{g}_{i}) \\
C_{i}+1 & \text{それ以外}
\end{cases}
\end{align}
$i$は探索点番号, $j$はランダムに決定された次元番号, $g$は世代数, $m$はランダムに決定された探索点番号を表します. $\phi$は$[-1, 1]$の範囲で発生する一様乱数, $\phi$は$[0, R]$の範囲で発生する一様乱数, $x_{i}$は探索点$i$の位置,$v_{ij}$は
$x_{ij}$の更新候補探索点, x_{bestj}は現時点での最適なパラメータ, $f_{i}$は個体$i$の適応度, $C_{i}$は連続して探索点n$i$の位置が更新されなかった回数を表します.
Rに関しては参考にした論文では1.5としています。
##ステップ3 Onlooker Bee
各探索点の相対適応度を算出し, ルーレット戦略により更新候補探索点を選択し, 以下の式により位置を更新します.
\begin{align}
p^{g}_{i} &= \dfrac{f^{g}_{i}}{\sum^{N}_{n=1}f^{g}_{n}} \\
P^{g}_{i} &= \sum_{j=1}^{i}p^{g}_{j} \\
c &= \displaystyle{\arg_{i \in N}}( P^{g}_{i} \leq \zeta \leq P^{g}_{i+1}) \\
v^{g}_{cj} &= x^{g}_{cj} + \phi^{g}_{cj}(x^{g}_{cj} - x^{g}_{mj})+\psi^{g}_{ij}(x^{g}_{cj} - x^{g}_{bestj}) \\
x^{g}_{cj} &=
\begin{cases}
v^{g}_{cj} & f_{c}(v^{g}_{c}) \leq f_{c}(x^{g}_{c}) \\
x^{g}_{c} & \text{それ以外}
\end{cases} \\
C_{c} &=
\begin{cases}
0 & f_{c}(v^{g}_{c}) \leq f_{c}(x^{g}_{c}) \\
C_{c}+1 & \text{それ以外}
\end{cases}
\end{align}
$i$は探索点番号, $j$はランダムに決定された次元番号, $g$は世代数, $m$はランダムに決定された探索点番号を表す. $\phi$は$[-1, 1]$の範囲で発生させる一様乱数, $\phi$は$[0, R]$の範囲で発生する一様乱数, $x_{i}$は探索点$i$の位置,
$v_{ij}$は$x_{ij}$の更新候補探索点, $f_{i}$は探索点$i$の適応度, $C_{c}$は連続して探索点$c$の位置が更新されなかった回数を表す.
$c$はルーレット選択により選択した探索点番号を表す. $\zeta$は$[0,1]$の一様乱数とする.
$p_{i}$は世代$g$における相対適応度を表し, $P_{i}$はルーレット戦略における選択確率を表す. $f_{c}$は世代$g$における適応度を表す.
##ステップ4 Scout Bee
更新されなかった探索点をランダムに割り振って探索点を更新します。
更新されなった回数を格納している変数に関しては0とします。
##ステップ5 最良点の更新
現時点の最良点が現時点までの最良点よりも良い場合は更新します。
更新後、終了条件になっているかどうかを確認し、なっていれば終了し、
そうでなければステップ2へ戻ります。
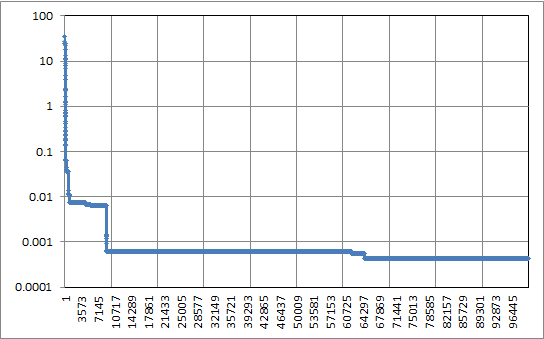
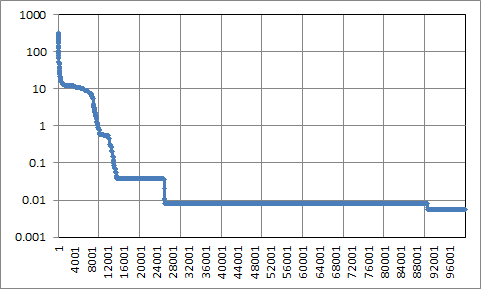
#実験
今度はrosenbrock関数で試してみました。次元数は10次元と50次元。
#ソースコード(Java)
計算に使用したソースコードは以下の通りです。前回と同じく乱数に関してはメルセンヌツイスターのライブラリである、Sfmt.javaを使用しています。詳細はこちら。
http://www001.upp.so-net.ne.jp/isaku/rand2.html
GAbcTestSimple.java
public class GAbcTestSimple
{
public static void main( String[] args)
{
int iGenerationNum = 100000;
int iAbcDataNum = 60;
int iAbcSearchNum = 30;
int iAbcVectorDimNum = 50;
int iAbcLimitCount = 180;
double lfSolveRange = 5.12;
// 初期化を行います。
Abc abc = new Abc( iGenerationNum, iAbcDataNum, iAbcVectorDimNum, iAbcSearchNum, iAbcLimitCount, lfSolveRange);
for( int i = 0;i < iGenerationNum; i++ )
{
// ABC法の計算を行います。
abc.vGAbc();
// 現時点での関数の最小値を出力します。
abc.vOutputGlobalMinAbcDataConstFuncValue();
}
}
}
Abc.java
public class Abc
{
private int iGenerationNumber; // 計算回数
private int iAbcDataNum; // コロニーの数
private int iAbcVectorDimNum; // 蜂の特徴ベクトル
private int iAbcSearchNum; // 探索点数
private int iAbcLimitCount; // 更新しなかった回数
private double[][] pplfAbcData; // ABCデータ配列
private double lfGlobalMaxAbcData; // 大域的最適値
private double lfGlobalMinAbcData; // 大域的最小値
private double[] plfGlobalMaxAbcData; // 大域的最適解を表す粒子のデータ
private double[] plfGlobalMinAbcData; // 大域的最適解を表す粒子のデータ
private double[][] pplfVelocityData; // ABCデータ速度配列
private double[] plfFitProb; // 適合度相対確率
private double[] plfFit; // 適合度
private int[] piNonUpdateCount; // 更新しない回数
private Sfmt rnd;
private double lfSolveRange; // 探索範囲
/**
* <PRE>
* 人口蜂コロニーの初期化を実行します。
* </PRE>
* @param iGenCount 計算回数
* @param iGenNum コロニー数
* @param iGenVectorDim 探索点の次元数
* @param iSearchNum 探索点の数
* @param iLimitCountData 更新しなかった回数
* @param iIntervalMinNum 最低反復回数
* @param iAlphaData 探索点上位数
* @param lfDrData 収束状況判定
* @param lfBoundData 適合度許容限界値
* @param lfAccuracyData 適合度評価精度
*/
public Abc( int iGenCount, int iGenNum, int iGenVectorDim, int iSearchNum, int iLimitCountData, double lfSolveRangeData )
{
int i,j;
iGenerationNumber = iGenCount;
iAbcDataNum = iGenNum;
iAbcVectorDimNum = iGenVectorDim;
iAbcSearchNum = iSearchNum;
iAbcLimitCount = iLimitCountData;
lfSolveRange = lfSolveRangeData;
lfGlobalMaxAbcData = -Double.MAX_VALUE; // 大域的最適値
lfGlobalMinAbcData = Double.MAX_VALUE; // 大域的最小値
long seed;
seed = System.currentTimeMillis();
rnd = new Sfmt( (int)seed );
pplfAbcData = new double[iAbcDataNum][iAbcVectorDimNum];
pplfVelocityData = new double[iAbcDataNum][iAbcVectorDimNum];
plfFit = new double[iAbcSearchNum];
plfFitProb = new double[iAbcSearchNum];
piNonUpdateCount = new int[iAbcSearchNum];
plfGlobalMaxAbcData = new double[iAbcVectorDimNum];
plfGlobalMinAbcData = new double[iAbcVectorDimNum];
for( i= 0;i < iAbcDataNum; i++ )
{
for(j = 0;j < iAbcVectorDimNum; j++ )
{
pplfAbcData[i][j] = 0.0;
pplfVelocityData[i][j] = 0.0;
}
}
for( i = 0;i < iAbcSearchNum ; i++ )
{
plfFit[i] = 0.0;
plfFitProb[i] = 0.0;
piNonUpdateCount[i] = 0;
}
for( i = 0;i < iAbcVectorDimNum; i++ )
{
plfGlobalMaxAbcData[i] = 0.0;
plfGlobalMinAbcData[i] = 0.0;
}
for( i= 0;i < iAbcDataNum; i++ )
{
for(j = 0;j < iAbcVectorDimNum; j++ )
{
pplfAbcData[i][j] = lfSolveRange*(2.0*rnd.NextUnif()-1.0);
}
}
}
/**
* <PRE>
* 人工蜂コロニー最適化法を実行します。
* </PRE>
*/
public void vGAbc()
{
// employee bee の動作
vEmployBeeGBest();
// onlookers beeの動作
vOnlookerBeeGBest();
// scout bee の実行
vScoutBeeOrigin();
// 大域的最大値、最小値を取得します。
vGetGlobalMaxMin();
}
/**
* <PRE>
* Employ Beeを実行します。(GBest版)
* </PRE>
* @author kobayashi
*/
void vEmployBeeGBest()
{
int m,h;
int i,j;
double lfRand = 0.0;
double lfRand2 = 0.0;
double lfFunc1 = 0.0;
double lfFunc2 = 0.0;
// employee bee の動作
// 更新点候補を算出します。
m = rnd.NextInt(iAbcSearchNum);
h = rnd.NextInt(iAbcVectorDimNum);
for( i = 0;i < iAbcSearchNum; i++ )
{
lfRand = 2.0*rnd.NextUnif()-1.0;
lfRand2 = 1.5*rnd.NextUnif();
for( j = 0; j < iAbcVectorDimNum; j++ )
pplfVelocityData[i][j] = pplfAbcData[i][j];
pplfVelocityData[i][h] = pplfAbcData[i][h] + lfRand*( pplfAbcData[i][h] - pplfAbcData[m][h] ) + lfRand2*(plfGlobalMinAbcData[h] - pplfAbcData[i][h] );
// 各探索点と更新しなかった回数を格納する変数を更新します。
lfFunc1 = lfSphere( pplfVelocityData[i] );
lfFunc2 = lfSphere( pplfAbcData[i] );
if( lfFunc1 < lfFunc2 )
{
pplfAbcData[i][h] = pplfVelocityData[i][h];
piNonUpdateCount[i] = 0;
}
else piNonUpdateCount[i] = piNonUpdateCount[i] + 1;
}
}
/**
* <PRE>
* Onlooker Beeを実行します。
* </PRE>
*/
void vOnlookerBeeGBest()
{
int i,j;
int c,m,h;
double lfRes = 0.0;
double lfRand = 0.0;
double lfRand2 = 0.0;
double lfFitProb = 0.0;
double lfProb = 0.0;
double lfPrevProb = 0.0;
double lfFunc1 = 0.0;
double lfFunc2 = 0.0;
double lfObjFunc = 0.0;
lfRes = 0.0;
for(j = 0;j < iAbcSearchNum; j++ )
{
// 適応度の算出
lfObjFunc = lfSphere( pplfAbcData[j] );
lfFitProb = lfObjFunc;
lfRes += lfFitProb;
plfFit[j] = lfFitProb;
}
// 適応度の正規化
for( j = 0;j < iAbcSearchNum; j++ ) plfFitProb[j] = plfFit[j]/lfRes;
// ルーレット戦略を実行
lfProb = lfPrevProb = 0.0;
lfRand = rnd.NextUnif();
c = 0;
for( j = 0;j < iAbcSearchNum; j++ )
{
lfProb += plfFitProb[j];
if( lfPrevProb <= lfRand && lfRand <= lfProb ) c = j;
lfPrevProb = lfProb;
}
// ルーレット選択した探索点に対して更新候補を求めます。
// 更新点候補を算出する。
// 更新点候補を乱数により決定する。
m = rnd.NextInt(iAbcSearchNum);
h = rnd.NextInt(iAbcVectorDimNum);
lfRand = 2.0*rnd.NextUnif()-1.0;
lfRand2 = 1.5*rnd.NextUnif();
for( j = 0; j < iAbcVectorDimNum; j++ )
pplfVelocityData[c][j] = pplfAbcData[c][j];
pplfVelocityData[c][h] = pplfAbcData[c][h] + lfRand*( pplfAbcData[c][h] - pplfAbcData[m][h] ) + lfRand2*( plfGlobalMinAbcData[h] - pplfAbcData[c][h] );
// 更新点候補を次のように更新します。
lfFunc1 = lfSphere( pplfVelocityData[c] );
lfFunc2 = lfSphere( pplfAbcData[c] );
if( lfFunc1 < lfFunc2 )
{
for( j = 0;j < iAbcVectorDimNum; j++ )
pplfAbcData[c][j] = pplfVelocityData[c][j];
piNonUpdateCount[c] = 0;
}
else piNonUpdateCount[c] = piNonUpdateCount[c] + 1;
}
/**
* <PRE>
* Scout Beeを実行します。
* </PRE>
*/
private void vScoutBeeOrigin()
{
int i,j,k;
double lfRand = 0.0;
// 新たな探索点を求めて探索を実行します。
for( i = 0;i < iAbcSearchNum; i++ )
{
if( piNonUpdateCount[i] > iAbcLimitCount )
{
for( k = 0;k < iAbcVectorDimNum; k++ )
{
lfRand = rnd.NextUnif();
pplfAbcData[i][k] = lfSolveRange*(2.0*lfRand-1.0);
}
}
}
}
/**
* <PRE>
* 現時点での目的関数の全体を通しての最大、最小値を求めます。
* </PRE>
*/
private void vGetGlobalMaxMin()
{
int i,j;
int iMinLoc = 0;
double lfObjFunc = 0.0;
for( i = 0;i < iAbcSearchNum; i++ )
{
lfObjFunc = lfSphere( pplfAbcData[i] );
if( lfGlobalMinAbcData >= lfObjFunc )
{
iMinLoc = i;
lfGlobalMinAbcData = lfObjFunc;
for( j = 0; j < iAbcVectorDimNum; j++ )
plfGlobalMinAbcData[j] = pplfAbcData[i][j];
}
if( lfGlobalMaxAbcData <= lfObjFunc )
{
iMinLoc = i;
lfGlobalMaxAbcData = lfObjFunc;
for( j = 0; j < iAbcVectorDimNum; j++ )
plfGlobalMaxAbcData[j] = pplfAbcData[i][j];
}
}
}
/**
* <PRE>
* 現時点でのもっともよい粒子の位置を出力します。
* </PRE>
*/
public void vOutputGlobalMinAbcData()
{
int i;
// 現時点での各粒子の目的関数の値を出力します。
for( i = 0; i < iAbcVectorDimNum; i++ )
{
System.out.print( plfGlobalMinAbcData[i] + "," );
}
System.out.println("");
}
/**
* <PRE>
* 現時点でのもっともよい粒子の目的関数値を出力します。
* </PRE>
* @return 関数値
*/
public void vOutputGlobalMinAbcDataConstFuncValue()
{
// TODO 自動生成されたメソッド・スタブ
System.out.println( lfSphere( plfGlobalMinAbcData ) + "," );
}
/**
* <PRE>
* Sphere関数を実行します。
* </PRE>
* @param plfData ベクトルデータ
* @return Sphere関数の値
*/
private double lfSphere( double[] plfData )
{
double lfRes = 0.0;
for(int i = 0;i < plfData.length; i++ )
lfRes += plfData[i]*plfData[i];
return lfRes;
}
/**
* <PRE>
* rosenbrock関数を実行します。
* </PRE>
* @param plfData ベクトルデータ
* @return rosenbrock関数の値
*/
private double lfRosenbrock( double[] plfArgs )
{
int i;
double lfRes = 0.0;
double lfTempX1 = 0.0;
double lfTempX2 = 0.0;
double lfXX = 0.0;
for( i = 0;i < plfArgs.length-1; i++ )
{
lfXX = plfArgs[i]*plfArgs[i];
lfTempX1 = 1.0-plfArgs[i];
lfTempX2 = plfArgs[i+1]-lfXX;
lfRes += (100*lfTempX2*lfTempX2+lfTempX1*lfTempX1);
}
return lfRes;
}
}
#参考文献
Guopu Zhu, Sam Kwong, "Gbest-guided artificial bee colony algorithm for numerical function optimization," Applied Mathematics and Computation, vol.217 (2010) pp.3166–3173