概要
以前の私のモンテカルロ法の記事の内容を使って、イジングモデルを解いて見ましょうというのが、今回の趣旨です。
相転移とイジングモデル
相転移とは、固体が溶けて液体になったりというような身近な物理現象です。物性物理の世界では、強磁性体だった磁石が温度を上げると急に磁石ではなくなったり、超伝導が常伝導になったりというような現象があります。
これら相転移は、平たく言えば隣同士の原子や分子やスピンなどの相互作用が、温度などによって微妙に変化するだけで、長距離の秩序が急に現れたり、急に消えたりする現象です。
相転移をシミュレーションしてみよう、イジングモデルとメトロポリス法
それでは相転移をモンテカルロ法によってシミュレーションすることを考えていきましょう。モデルとして、今回は2次元の正方格子を考えて、温度が$k_B T$のとき、格子点にスピン+1か-1の粒子をランダムにばらまいたとしましょう。ばらまかれたスピンは、温度と周辺のエネルギーの大小によって反転することができます。このようなモデルをイジングモデルと言います。
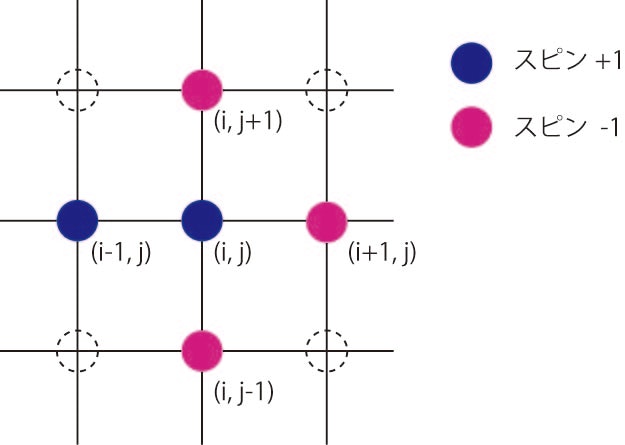
ある点$(i, j)$は格子の端でない限り、必ず4点に囲まれています。そこで周りの4点のスピン間の相互作用だけを考えて、それ以上離れたスピンの相互作用は考えないことにします。スピン同士の相互作用の係数(これを交換相互作用と呼びます)を$J$とすれば、点$(i, j)$のハミルトニアンは
H_{i, j} = -J (S_{i+1, j}+S_{i-1, j}+S_{i, j+1}+S_{i, j-1}) S_{i, j}
となります。かみ砕いて説明しますと、まず"ハミルトニアン"="エネルギー"だと思ってください。ばらまかれた$S_{添字}$は$\pm 1$のどちらかに決まっているので、例えば$J=1$とすれば、下図の場合、中心がスピン+1でその周りに-1が3つ、+1が1つあるので、
H_{i, j} = - (-1+1-1-1) \times 1 = 2
と求まります。
つまり座標$(i, j)$のエネルギーは2だということがわかります。0より大きいのでエネルギーが高い状態になっていることもわかりました。ここから、$J=1$のとき、周りの3点のスピンは$-1$なので、点$(i, j)$のスピンも+1でいるよりは-1に反転した方がエネルギー的に得だということがわかります。反転する前と後のエネルギーの差$\Delta E$は
\Delta E = H_{i, j 後} - H_{i, j 前} = -2 H_{i, j前}
となります(今の例では-2-2=-4)。そこで、点$(i, j)$のスピンが反転するかしないかの確率を、統計力学で出てくる確率因子
\exp(-\Delta E /k_B T) = \exp(2H_{i, j} /k_B T) \equiv p
で決めることにします。つまり、スピンが反転して得をするエネルギーが、温度$k_B T$に比べて大きければ大きいほど、反転する確率$p$を高く設定しているということです。
具体的には0~1を取り得る乱数$r$を発生させ、$r < p$なら反転、$r > p$なら反転させないと決めます。これをメトロポリス法と呼びます。
シミュレーションスクリプト
以下に上述の計算を行うスクリプトを示します。
# !/usr/bin/env python
import matplotlib.pyplot as plt
import numpy as np
class IsingSingleSpinFlip:
def __init__(self):
# set region range of x, y
self.XMAX = 50
self.YMAX = 50
# set J_ij (= J, uniform)
self.J = 1.0
# set h_i (= H, uniform)
self.H = 0.0
# set initial condition (-1 or 1, random)
self.S = (np.random.rand(self.XMAX, self.YMAX)<0.5) * (-2) + 1
# set 1/(k_b T)
self.ONEOKBT = 1.0
# set the number of iteration
self.ITER = 1000000
def flip_probability_matrix(self, i, j):
# compute Hamiltonian @ (i, j) position
h_ij = -1 * (self.J*(np.roll(self.S, 1, 0)[i][j]
+np.roll(self.S, -1, 0)[i][j]
+np.roll(self.S, 1, 1)[i][j]
+np.roll(self.S, -1, 1)[i][j])
+self.H) * self.S[i][j]
# calculate & return probability of spin flip
p = np.exp(2*h_ij*self.ONEOKBT)
p = np.minimum(p, 1.0)
return p
def plot_spin(self):
# remove previous figure
plt.clf()
# plot color map
plt.imshow(self.S, cmap='PuOr')
# add colorbar
plt.colorbar(ticks=[-1, 1], orientation='vertical')
# set pause interval time
plt.pause(0.0001)
def run(self):
# main loop start
for n in range(self.ITER):
# set spin flip position randomly
i = np.random.randint(0, self.XMAX)
j = np.random.randint(0, self.YMAX)
# compute flip probability
p = self.flip_probability_matrix(i, j)
# if flip spin, valur of 'flip' is -1, otherwise 1
flip = (np.random.rand()<p) * (-2) + 1
# update S matrix
self.S[i][j] *= flip
# plot
if n % 1000 == 0:
self.plot_spin()
if __name__ == '__main__':
a = IsingSingleSpinFlip()
a.run()
スクリプト詳細
__init__
ここで色々な計算条件を設定しています。self.XMAX self.YMAXでそれぞれ$x, y$方向のスピンの数を設定します。self.Jは交換相互作用係数、self.Hは外部の縦磁場、self.ONEOKBTは$1/k_B T$の大きさをそれぞれ表します。self.Sはスピン$\pm 1$がランダムに並んだ2次元リストで、これを初期条件としています。self.ITERはモンテカルロ法の試行回数です。
flip_probability_matrix
この関数で座標$(i, j)$のスピンの反転確率を計算しています。ここでの計算にnumpyのroll関数を巧みに利用しています。$(S_{i+1, j}+S_{i-1, j}+S_{i, j+1}+S_{i, j-1}) S_{i, j}$の計算、さらに周期境界条件を簡単に計算できます。
numpy.roll
この関数はある行列の行あるいは列をシフトさせたいときに使う関数です。例えば
>>> x = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> y = np.roll(x, 1, 0)
>>> y
>>> array([[7, 8, 9],
[1, 2, 3],
[4, 5, 6]])
この例では3x3の2次元行列を1行シフトしています。3つめの引数はaxisを意味しており、この値を1に変えると
>>> z = np.roll(x, 1, 1)
>>> z
>>> array([[3, 1, 2],
[6, 4, 5],
[9, 7, 8]])
のように、列を1列シフトすることができます。
plot_spin
ここでmatplotlibを用いてself.S($\pm 1$のスピンの並び)を2次元カラーコントアとして描画しています。
run
この関数でメトロポリス法を用いてスピンの並びであるself.Sを更新しています。
i = np.random.randint(0, self.XMAX)
j = np.random.randint(0, self.YMAX)
で着目する座標$(i, j)$のスピンを指定しています。
flip = (np.random.rand()<p) * (-2) + 1
で乱数$r$とスピン反転確率$p$の大小を判定しています。Trueなら-1となり、座標$(i, j)$のスピンを反転、falseなら1となり反転しないを選択しています。
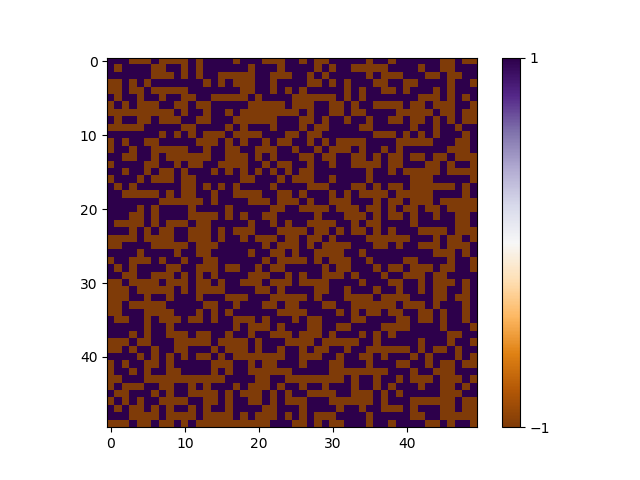
結果
self.XMAX = 50
self.YMAX = 50
self.J = 1.0
self.H = 0.0
self.ONEOKBT = 1.0
self.ITER = 1000000
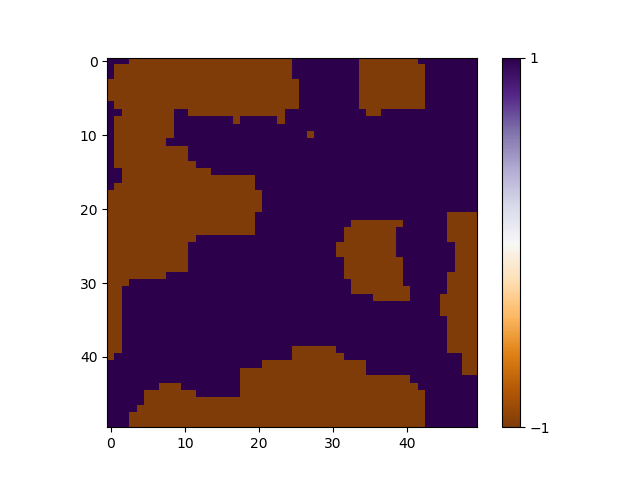
上述のパラメータで出力した結果がこちらです。
時間が経過すると、スピンが揃った比較的大きな領域(ドメイン)に成長していくことがわかります。ここで注目したいのは相互作用は隣同士の4つ(短距離相関)しか考慮されていないのに"大きな領域"という長距離の秩序が次第に現れていく点です。
結言と応用例
ここまでで、磁性体のシミュレーションをモンテカルロ法を用いて行ってきました。しかし強磁性体なんて興味ない、という方のために少し違った見方をご紹介して、この記事の結言とします。
応用例として、スピンの代わりに電気のon, offで考えてみましょう。我々の脳は、脳細胞でできていますが、その脳細胞の活動は突き詰めて言えば、脳細胞の電位が上がること(発火)で機能しています。脳細胞はシナプスという"電線"で繋がっているので、イジングモデルの各点を脳細胞、スピンを脳細胞の発火、結合係数$J$を脳細胞同士の結合の強さと考えれば、イジングモデルで脳の神経回路をモデル化すること可能となります。このようなモデルは一般的にはニューラルネットワークと呼ばれるものです。特にモンテカルロ法を用いたものは確率的ニューラルネットワークと呼ばれ、脳の連想記憶と関係が深いと言われています。また画像のノイズ除去や誤り符号訂正などにも利用されています。興味がある方はスピングラス理論と情報統計力学などを併せて読むと面白いでしょう。