問題
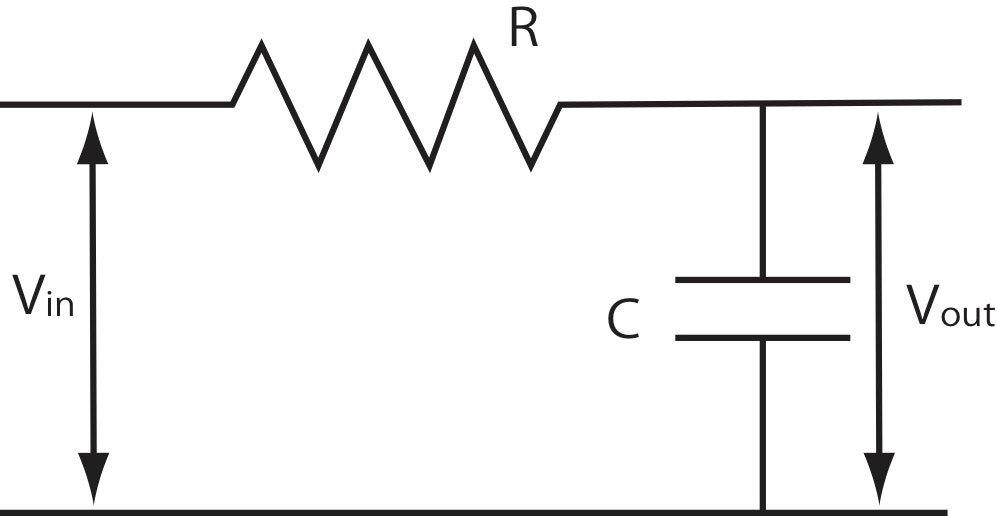
以下の図のようなRC回路において$V_{\rm out}$の計算を行い、その定性的解釈を考察しなさい。
解答例
パルス電圧をかけてみる
$RC$回路のコンデンサの両端に$V(t) = V_0 \delta(t)$というパルス電圧を掛けたとき、出力電圧がどうなるかを考えましょう。
時刻$t$でコンデンサに蓄えられている電荷を$Q(t)$とすると
V_{\rm out} (t) = \frac{Q(t)}{C} \\
I (t) = \frac{dQ(t)}{dt}
キルヒホッフ則より
V_{\rm in} - R I(t) -\frac{Q(t)}{C} = 0
\therefore \ V_{\rm in} -RC\frac{dV_{\rm out}}{dt}-V_{\rm out} = 0
\ \Longleftrightarrow \ RC\frac{dV_{\rm out}}{dt} + V_{\rm out}
= V_{\rm in}
この式の解を求めるために、まずは
RC\frac{dV_{\rm out}}{dt} +V_{\rm out} = 0
の解を考えます。
\frac{dV_{\rm out}}{dt}
= - \frac{1}{RC} V_{\rm out}
\ \Longrightarrow \ \int \frac{dV_{\rm out}}{V_{\rm out}}
= - \frac{1}{RC} \int dt \ \Longrightarrow \ \log |V_{\rm out}|
= - \frac{1}{RC} t + C_1 \ \Longrightarrow \ |V_{\rm out}|
= e^{-\frac{t}{RC} + C_1}
= e^{C_1} e^{-\frac{t}{RC}} \\
\ \Longrightarrow \ V_{\rm out}
= C_2 e^{-\frac{t}{RC}}
$C_1, C_2$は定数です。よって先程の式の解を
V_{\rm out} (t) = f(t) e^{-\frac{t}{RC}}
の形で求めましょう。これを元の式に代入すると
V_{\rm in}
= RC \left( \frac{df}{dt} e^{-\frac{t}{RC}} -\frac{1}{RC} e^{-\frac{t}{RC}} f(t)\right) + f(t) e^{-\frac{t}{RC}}
= RC \frac{df}{dt} e^{-\frac{t}{RC}}
今、$V_{\rm in} = V_0 \delta(t)$のようなパルス電圧を考えているので、これを代入します。
\frac{df}{dt}
= \frac{V_0}{RC} e^{t/RC} \delta(t)
\underbrace{=}_{\delta 関数の性質より} \frac{V_0}{RC} \delta(t) \ \Longrightarrow \ f(t) = \frac{V_0}{RC} \int \delta(t) dt = \frac{V_0}{RC} \Theta(t) + C_3
ここで$\Theta(t)$はヘヴィサイド階段関数で
\Theta(t) = \left\{ \begin{array}{lll}
1 & (t>0)\\
0 & (t<0)
\end{array} \right.
です。
\therefore V_{\rm out} (t)
= \left( \frac{V_0}{RC} \Theta(t) + C_3\right) e^{-\frac{t}{RC}}
$t<0$で$V_{\rm out}=0$より$C_3 = 0$。よって
V_{\rm out}(t) = \frac{V_0}{RC} e^{-\frac{t}{RC}} \Theta(t)
$\tau \equiv RC$は時定数と呼ばれます。exponentialの肩を見ればわかるように、時定数は「パルスとして入力された電圧が0と見なせるようになるまでにかかる時間」を現れます。過渡現象などとの式と見比べてみると楽しいでしょう。
フーリエ変換してみる
得られた結果をFourier変換し、出力電圧のスペクトルを見て見ましょう。
\hat{V}_{\rm out}(\omega)
= \frac{1}{2\pi} \int_{-\infty}^\infty V_{\rm out} (t) e^{i\omega t} dt
= \frac{v_0}{2\pi RC} \int_0^\infty e^{(i\omega-\frac{1}{RC})t} dt
= \frac{v_0}{2\pi RC} \frac{1}{i\omega-\frac{1}{RC}} \left| e^{(i\omega-\frac{1}{RC})t}\right|_0^\infty
= \frac{v_0}{2\pi RC} \frac{-1}{i\omega-\frac{1}{RC}} \\
= \frac{v_0}{2\pi RC} \frac{RC}{1-i\omega RC}
= \frac{v_0}{2\pi} \frac{1+i\omega RC}{1+\omega^2 R^2C^2}
$\hat{V}(\omega)$は複素数なので、物理的に意味のある量としてその大きさをとってみます。
\left| \hat{V}_{\rm out} (\omega) \right|
= \frac{v_0}{2\pi \sqrt{1+\omega^2R^2C^2}}
また位相を$\theta$として
\hat{V}_{\rm out}(\omega) = \left| \hat{V}_{\rm out} (\omega) \right| e^{i\theta} = \left| \hat{V}_{\rm out} (\omega) \right| (\cos \theta + i \sin \theta)
のように書いたとき、$\hat{V}(\omega)$式の結果と比較すると
\cos \theta
= \frac{1}{\sqrt{1+ \omega^2R^2C^2}},
\sin \theta
= \frac{\omega RC}{\sqrt{1+ \omega^2R^2C^2}}
\ \Longrightarrow \ \theta
= \tan^{-1} (\omega RC)
のようになります。
式計算ののちに、直感的に説明してみる
$\hat{V}_{\rm in}(\omega)$について考えてみると
\hat{V}_{\rm in}(\omega)
= \frac{V_0}{2\pi} \int_{-\infty}^\infty \delta(t)e^{i\omega t} dt
= \frac{V_0}{2\pi}
よって$V_{\rm in} (t)= V_0 \delta(t)$は初期位相$0$、大きさ$V_0/2\pi$の全ての角周波数の波が重ね合わさったものと考えることができます。一方で$V_{out}$では、角周波数$\omega$の波は$\tan^{-1} (\omega RC)$だけ位相が遅れ、大きさは$\displaystyle{\frac{V_0}{2\pi \sqrt{1+\omega^2R^2C^2}}}$になります。角周波数が大きいほど大きさが小さくなるから、これはローパスフィルタとしてはたらくことがわかります。分母を見てみると、$1<\omega^2R^2C^2$のとき、すなわち
\omega_c > \frac{1}{RC} \ \left(周波数の場合にはf_c > \frac{1}{2\pi RC} \right)
のとき2乗の効果により減少が著しくなる事がわかります。この周波数のことをカットオフ周波数と呼びます。カットオフ周波数は時定数の逆数となっていこともわかります。
物理的解釈:交流ではわかりにくいので、$V_{\rm in}$として直流電源(電池)の+, -を交互に入れ替えるような実験をしたとしましょう。もしこの入れ替え作業が早ければ、コンデンサには十分な電荷が蓄えられる前に+, -が逆転してしまうために、コンデンサには電荷が蓄積されず、すなわちコンデンサの電圧$V_{\rm out}$は検出されなくなってしまいます。一方、+, -の入れ替え作業が遅ければ、コンデンサに電荷が貯まるまでに十分な余裕があるために、コンデンサの電圧が$V_{\rm out}$として検出されます。コレがローパスフィルタの物理的な(直観的な)理解です。