概要
D-Wave量子コンピュータで少し(?)注目を浴びた磁束量子。量子力学では観測量が量子化されます。つまり磁束(磁場x面積)も量子化されて、とびとびの値になるのです。このとびとびの値の基準となるものを磁束量子と呼びます。具体的な値としては
\Phi_0 = \frac{hc}{2e} \sim 2.07 \times 10^{-7} \rm{[G cm^{-2}]} \tag{1}
です。ここで$\hbar, c, e$はそれぞれプランク定数$h$を$2\pi$で割ったディラック定数、光速の大きさ、電気素量です。これを古典力学と電磁気学、そして量子力学の入り口で必ず習うド・ブロイ波を利用して導出してみましょう。以下ではcgs単位系で説明していきます。
いざ、物理の世界へ
古典力学、円運動している電荷に働く遠心力
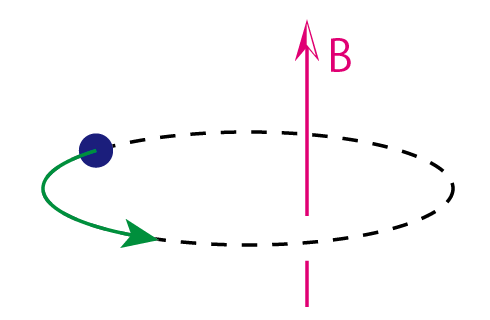
以下の図のように、磁場中で等速円運動している電子(電荷$-e$, 質量$m_e$)を考えましょう。
円運動している電子に働く、遠心力の大きさは
m_e \frac{v^2}{r}
と書かれます。ここで、$v$は電子の速度、$r$は円運動の半径です。
電磁気学、電子が磁場中を運動することにより働く力
高校物理のフレミングの左手の法則を思い出すと、電子に働くローレンツ力は
-ev \frac{B}{c}
となります。cgs単位系なので、磁場の大きさが$1/c$倍されていることに注意してください。
再び古典力学、力の釣り合い
電子が等速円運動を行うためには、上の2つの章で説明した二つの力が釣り合っている必要があります。すなわち
m_e \frac{v^2}{r} = e v \frac{B}{c}
です。これを式変形して
m_e v = \frac{eB}{c} r
量子力学、ド・ブロイ波
量子力学では運動量$p$を持つ物質は、波数$k (= 1/\lambda)$の波として
p = m_e v = \hbar k = \frac{\hbar}{\lambda}
と表されることが知られています(これは受け入れましょう)。ここで$\lambda$は波長を表します。これをド・ブロイの物質波と呼びます。
式変形
これらの数式から
\frac{\hbar}{\lambda} = \frac{eB}{c} r \tag{2}
境界条件
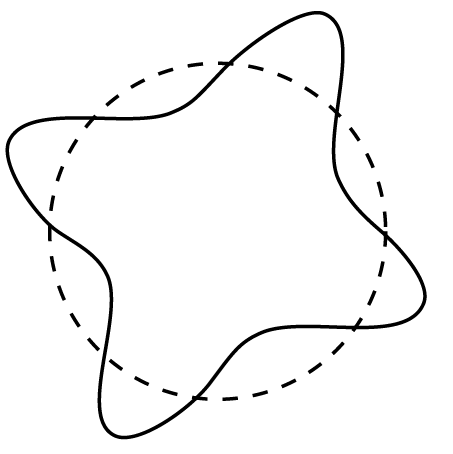
量子力学から、重要な境界条件が発生します。それは「電子が一定の半径の場所で等速円運動しているなら、それは定在波であるべき」というものです(下図参照)。
もし電子が定在波でなければ、一周回ってきた波動関数と一周前の波動関数が干渉して、打ち消しあってしまいます。波動関数が打ち消しあうということは電子の存在確率がなくなってしまうことを意味しますので、電子が一個等速円運動をしているということと矛盾してしまいますね。
この条件から
2\pi r = \lambda n \tag{3}
となります。ここで$n$は1波長の数、すなわち正の整数です。
磁束量子
(2), (3)式の変形を行うことによって
\pi r^2 B = \Phi_0 n
という式を導出することができます。ここで左辺は半径$r$の円の面積 x 磁場ですから、これは磁束を表します。見事に磁束が量子化されている式を導くことができました。
これをどのように量子コンピュータに応用したのか?
厳密には磁場の向きには、上向き・下向きが存在しますから、$n = 0, \pm 1, \pm 2 \cdots$のようにマイナスも取りうることになります。
D-Waveのような磁束量子ビットを原理として用いているものでは、$-\Phi_0$をスピンがダウン、$\Phi_0$をスピンがアップの状態として扱っているのです。
結言
古典力学、電磁気学、量子力学の根幹でありながら最初の方で必ず学ぶド・ブロイ波、そして境界条件からこうあるべき、という式から、磁束量子を導出することができました。