世間の「ショアのアルゴリズムで素因数分解」の解説に腹落ちできない。理由は
1. 素因数分解の例として挙げている数が15や21などあまりにもしょぼい
2. 量子位相推定で用いる制御ユニタリー(べき剰余)の説明や実装例がない
3. オラクルを作る別法では予め位数が分かっていなければならない
例外はあるがそんな解説が多すぎ! そこで、とりわけ「ショアのアルゴリズム」に初めて接する人が私のように戸惑わないように、あるいはショアアルゴリズムが腑に落ちない人に向けて、何故、上記のようなことになってしまうのか、アドベントカレンダーへ投稿 ...なんて... この投稿では件のべき余剰の概説とblueqatでの実装を示すが、分かり易いとの以下の文献を基にしている。
Stephane Beauregard (2003),Circuit for Shor’s algorithm using 2n+3 qubits, Quantum Information and Computation, Vol.3, No.2 pp.175-185 also on arXiv:quant-ph/0205095
1.素因数分解の例として挙げている数がしょぼい件
「RSA等の公開鍵暗号の安全論拠は大きな数の素因数分解にはスパコンですら1億年級の計算時間がかかってしまい実質的に解読されないこととされる。ところが量子コンピュータが実用的になればショアのアルゴリズムで素因数分解があっという間に解けてしまうため公開鍵暗号が使い物にならなくなる」
「ショアのアルゴリズムで素因数分解」の解説では概ねこんな感じでその意義が紹介される。大きな数とは?2048ビット長のRSAでの桁数は617桁。ピントこないかもしれない。1兆×1兆×1兆×1兆×1兆でさえ60桁。1兆を50回掛けても未だ足りないぐらい巨大な数である。確かに大きな数でいかにも計算には骨が折れそうである。がしかし、解説でよく使われる数と言えば、なんと15や21! 二桁である。小学生でも瞬時に 15=3×5, 21=3×7 と分る。これでは617桁との差があまりに大きすぎて誇大広告! これにはいくつかの事情が推定される。
・実機1 にせよシミュレーター(SDK)にせよ量子ビット数が少なく大きな桁を扱うことが困難
・解説に好例とできる数値が少ない
諸事情はあるにせよ15と21ではしょぼすぎ。せめて暗算では浮かばない程度の3桁か4桁、願わくば8桁ぐらいの例が欲しい。ところが実のところ解説として説明しやすくかつ理解しやすい好例となる数値を見つけるのは存外大変。その辺りを検証するためにまず大雑把にアルゴリズムを概観してみよう。
1-1.ショアのアルゴリズム超概観
素因数分解の対象となる数をN、Nと互いに素でNより小さい任意で選んだ自然数をaとする。$$f(x)=a^x,mod,N\quad (x=0,1,2,...)\qquad(式1)$$式の意味は $a^x$ をNでわったときの余りを f(x) とするということ。x=0の時はf(0)=1、xを大きくしていき次にf(x)=1となるxを位数といい r で表す。実はこの関数は周期性がありf(x)=f(x+r)となっている。位数 r が分かると以下の式から N の二つの因数が求まる。(r が偶数の時のみ)
$$gcd(a^{r/2}±1,,N)\qquad(式2)$$ここでgcdとはカッコ内のカンマで区切られた2つの数の最大公約数を意味している。ショアのアルゴリズムでは位数を見つける方法として量子位相推定(以降QPE)でf(x)の周期を見つけることを肝としている。QPEでユニタリー演算の周期を求める方法は量子位相推定をグローバーやセルオートマトンに適用してみたをご参照。<以下、次節まで読み飛ばし可!> 参照先の図1にあるようにQPEではユニタリー演算Uを $U^{2k}\quad k=0,1,2,...$と繰り返し適用していく必要があるが、一方、先ほどの(式1)では $a^x$ のxをインクリメントさせていく。このxのインクリメントと U の適用回数とがどう繋がっていくのか?ここを説明してる解説も少ない気が? まさにここを繋げるような以下のユニタリーUを考えるわけである。
$$U|y>=|a,y\quad mod\quad N>\qquad(式3)$$式3から以下のようにUの適用回数がxのインクリメントとなっていることが分かる。$$U|a^x,mod,N>=|a^{x+1},mod,N>\\U^2|a^x,mod,N>=U|a^{x+1},mod,N>=|a^{x+2},mod,N>\\U^{2k}|a^x,mod,N>=|a^{x+2k},mod,N>\qquad(式4)$$
従って、式1の関数の周期=位数は式3のユニタリーにQPEを適用することで、ほぼ求まることになる。では、このべき余剰のユニタリーの具体的な量子ゲートは?まずはDraper加算器(QFT加算器)、次にそれを用いたBeauregard加算器(剰余加算器)、次にそれを用いた剰余乗算器、そしてそれを用いたべき余剰と、それはそれはとても面倒である。そのことは後で分かる。その前に…
1-2.Nの例
話を元に戻そう。解説記事のためにせめて3桁以上ある N の具体例を探すことを考えよう。N 以外に a も同時に見つけなくてはならない。尚且つ r は偶数でなくてはならない。任意の互いに素な a と N で x を増加させながら計算し、f(r)=1 となるまで繰り返して見つける。まずは世間の解説にある N=15、a=7 の例(以下の折りたたみ内)でみてみよう。
**世間の例**
ご覧の通り a が7と小さく、位数も4であり比較的見つけやすい。また紙面が少なくて済みそう。が次の例(折りたたみ内)ではどうであろう。
**好ましくない例**
N に関わらず a が大きく r も大きいと $a^r$ がとてつもなく大きな数となってくる。従って現実的に計算しやすい数で見いだせる組み合わせは存外少ない。だが N が大きくても時として r が小さい組み合わせも存在しはする。例えば 位数 r=2 では特殊なケース として、二つの素数 A,B の差が2のとき、つまり |A-B|=2のとき、N=A×B、a=(A+B)/2 の組み合わせで r=2 となる。1万以下の 2 差の素数の組み合わせ中最大は、9857 と 9859。これから N=97180163、a=9858 となるが r=2 である。以下の折りたたみ内に解説に好例と思われる N,a,r の組み合わせを載せた。当然、大きな数の場合、べき余剰からの位数発見は量子ビットの制約からほぼ困難ではあるが。
**好ましい例**
2. 制御ユニタリー(べき余剰)の説明がない件
これにも大人の事情が推定される。例えば、
・この制御ユニタリーゲートはかなり煩雑である点
・量子ビット数の制限から制御ユニタリーゲートを実装するのが困難である点
・ショアのアルゴリズムにとって制御ユニタリー(べき余剰)の説明は本質部分ではないとの点
・さらには解説者自身が理解できていない(的なものがネットで複数あり、まさに大人の事情かと?)
とは言うものの、この部分の説明がなくては、とりわけ門外漢の投稿者などには腹落ちできない大きな原因となる。三つ目、四つ目の点はともかくとしても何故、煩雑なのか?何故、量子ビットをそこまで使用してしまうのか?べき余剰の第一歩とも言うべき加算器(減算器)からして桁上がり云々で Ancilla bit (補助的なビット)が必要となる。次のプロセスでも Ancilla bit が必要でさらにこれらのビットは基本的に、使い終わった後 "ゼロ化" しなくてはならず、そのためにまたビットを消費してしまう。ここからは、ビット数少なくかつ「ショアのアルゴリズム」に初めて接する方が戸惑わないよう、べき余剰の説明を試みよう。とは言えややこしい。かえって理解を損なう?そんな配慮からこの解説を避けたくなるのかもしれない。
2-1.QFT加算器(別名 Draper加算器)
文献は、T. Draper (2000), Addition on a quantum computer, also on arXiv:quant-ph。
要は計算基底をフーリエ変換(QFT=Quantum Fourier Transform)し、位相上で足し算、逆フーリエ変換で戻すアルゴリズムである。計算基底上で、論理ゲート的に足し算を構成すると複雑でかつ量子ビットを消費してしまう。しかし、QFTでフーリエ基底(z軸回りの位相φ)に変換してしまえば足し算がとても楽になる。ビットの消費も少なくてすむ上、理解し易い。
直感的には、a+b を考えた場合、まず整数 b をQFTでz軸回りの位相 φ に情報変換する。一方、整数 a はフーリエ変換するのではなく、a(二進数)の桁に応じた相当量の回転を、その桁が'1'の時にのみ、bの位相に加える。相当量の回転角とは、LSB側から勘定してk桁目では、$θ=2\pi/2^{k+1}$ 。回転角への加算であればアナログ的に足し算できるイメージである。図1に量子回路図を示した。
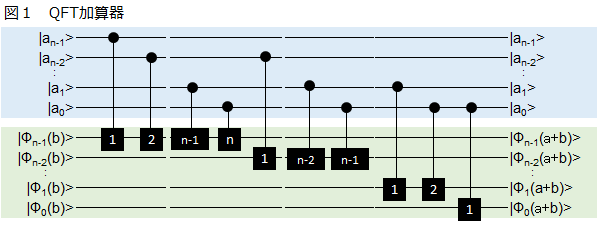
|φ(b)>のφはフーリエ基底を現しており、計算基底|b>にQFTを行いフーリエ基底にした状態を意味する。黒い四角はz軸回転のゲートを現しaの二進数でのMSB側からの制御回転ゲートとなっている。数字は前述した回転角度θを計算するときのkの値である。エンディアン(LSBとMSBの方向)に注意!すると、結果として|φ(a+b)>が出てくる。これを逆フーリエ変換(iQFT)すれば、a+b が得られる。
ここで、量子ビット数を減らすトリックとして、aを定数と考えてしまう …とは… a は量子ビットの変数にせず、古典状態のaの二進数で表し、if文で制御してしまう。つまり1の時は、先ほどの回転ゲートを実行、0なら実行せずを古典制御するのである。あたかも、そういうゲートであったかのように扱ってしまうのである。そうすると、この加算は、bのビット数のみで済むこととなる。例えば16ビットあれば合計で65535までの加算ができてしまう。尚、この加算モジュールを全くの逆順に実行すると減算が実現される。
さてblueqatで実装したものを示そう。本質的なモジュールは、qadder(constx)=加算モジュールと、qrevadder(constx)=減算モジュール、引数 constx は定数 a の二進数リストを逆順化したものである。変数 b は入力した十進を N 桁の二進数にし、inital_a 配列に入れ、それを、量子ビット0番からN-1番に割り当てている。割り当て方法は後述に参照を記す。
# -------- q-adder -----------------------------------------------------------
def qadder(constx): #加算器(引き数constxは定数aの二進数の逆順にしたリスト)
for i in range(N):
bi=N-i-1 #biは変数bの二進数のbi桁目のqubit番号
for j in range(bi,-1,-1):
if constx[j]==1: #定数の二進数のこの桁が1で実行
ang=(2*np.pi)/(2**(bi-j+1)) #回転角
c.rz(ang)[bi] #bi番目のqubitにang度分回転
return
# -------- q-reversed adder ---------------------------------------------------
def qrevadder(constx): #減算器(加算器とは全て逆順で構成している)
for bi in range(N):
for j in range(bi+1):
if constx[j]==1:
ang=(-2*np.pi)/(2**(bi+1-j))
c.rz(ang)[bi]
return
その他、付加的な量子アルゴリズムのモジュールはQFT()、逆フーリエ変換IQFT()、swapN()だけである。これらのモジュール部分を以下の折りたたみ内に記す。
**付加的な量子アルゴリズム部分**
# -------- QFT -----------------------------------------------------------------
def QFT():
for i in range(N):
for j in range(i):
c.cu1(np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- inversed QFT -------------------------------------------------------
def IQFT():
for i in range(N):
for j in range(i):
c.cu1(-np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- swap ----------------------------------------------------------------
def swapN():
Nh=int(N/2)
for i in range(Nh):
c.swap[i,N-i-1]
return
手順は、まずa,bの十進数を入力。それを二進数化。aはリスト化し逆順に。bは二進化し、その1,0の組み合わせを0番からN-1番の量子ビットに割り当てる。その後、0番からN-1番の量子ビットにQFT(このQFTモジュールは実行後にswapが必要)を実行。その後、核心部であるadderに。後は、0番からN-1番の量子ビットにIQFT(このIQFTモジュールも実行後にswapが必要)で計算基底に戻す。
実際に実行するには他にもモジュールや手続きが必要でプログラム全体を以下の折りたたみに示した。入力やコンソール出力にはqcamモジュールが必要で、このqcamモジュールの使い方等は【数式なしの量子コンピュータ】新視点セルオートマトンとグローバー 2回目の「2-1.q-camの構造とモジュール」に記載している。なかでもinital_a配列に入れた0,1の組を、量子ビット0番からN-1番に割り当てるのには、qcam.propinit(N,c,initial_a)を使用している。この原理は上記2回目内の「2-2. 1,0ではない確率的初期状態(ry 又は rx 又は u3 ゲートで作る)」を参照されたし。また、結果の抽出に関しては、上記2回目内の「2-3. Blueqatの状態ベクトル表示からのベクトルと確率の抽出」を参照されたし。その他、十進数をN桁の二進数のリストに変換するモジュールdtb(deci)があるが、ご覧の通りであり解説不要也や。
**qft-adder.py(全体)**
# q-adder by Gigagulin 2021 Nov.
from blueqat import Circuit
import numpy as np
import qcam
# -------- Setting --------------------------------------------------------------
N=16 # numaer of qubit
initial_a=np.array([0]*N,dtype='int') # b
const=np.array([0]*(N-1),dtype='int') # a constant
# -------- QFT -----------------------------------------------------------------
def QFT():
for i in range(N):
for j in range(i):
c.cu1(np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- inversed QFT -------------------------------------------------------
def IQFT():
for i in range(N):
for j in range(i):
c.cu1(-np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- q-adder -----------------------------------------------------------
def qadder(constx): #加算器(引き数constxは定数aの二進数の逆順にしたリスト)
for i in range(N):
bi=N-i-1 #biは変数bの二進数のbi桁目のqubit番号
for j in range(bi,-1,-1):
if constx[j]==1: #定数の二進数のこの桁が1で実行
ang=(2*np.pi)/(2**(bi-j+1)) #回転角
c.rz(ang)[bi] #bi番目のqubitにang度分回転
return
# -------- q-reversed adder ---------------------------------------------------
def qrevadder(constx): #減算器(加算器とは全て逆順で構成している)
for bi in range(N):
for j in range(bi+1):
if constx[j]==1:
ang=(-2*np.pi)/(2**(bi+1-j))
c.rz(ang)[bi]
return
# -------- swap ----------------------------------------------------------------
def swapN():
Nh=int(N/2)
for i in range(Nh):
c.swap[i,N-i-1]
return
# -------- deci to bin ------------------------------------------------------------
def dtb(deci):
binlist=np.array([0]*N,dtype='int')
tempo1_list=list(bin(deci)) # vector extraction butreversed. (Decimal to Binary)
del tempo1_list[0:2] # Delete '0','b' in tempo list
tempo1_list[0:0]=['0']*(N-len(tempo1_list)) # Zero-fill to adjust digits
for i in range(N):
binlist[i]=tempo1_list[i]
return binlist
# -------- Main Body --------------------------------------------------------------
c=Circuit(N)
print()
ao=input(' a(const)=')
bo=input(' b=')
tempo_a=dtb(int(ao))
initial_a=dtb(int(bo))
const_a = list(reversed(tempo_a))
qcam.propinit(N,c,initial_a)
QFT()
swapN()
# qadder(const_a)
qrevadder(const_a)
IQFT()
swapN()
master_a=np.array(c.run())
num,vector_a,prob_a=qcam.qvextract(N,1,1,master_a)
stdev,probability_a=qcam.qcalcd(N, num,vector_a,prob_a)
sum=0
for i in range(N):
sum=probability_a[N-i-1]*(2**i)+sum
print()
# print(' ',bo,' + ',ao,' = ',int(np.round(sum,decimals= 0)))
print(' ',bo,' - ',ao,' = ',int(np.round(sum,decimals= 0)))
2-2.剰余加算器(別名 Beauregard加算器)
次に、2-1.のQFT加算器を用いた剰余加算器(別名 Beauregard加算器)を説明しよう。いよいよ、剰余(モジュロ)がでてくる。整数 a+b を整数Nで割ったときの余りを求めるのが剰余加算器である。図2にその量子回路図を示した。図2では2-1.の加算器と減算器が組み合わされているだけで**割り算がない!**何故?素人である投稿者は、まず不思議に思ってしまうのだが、割り算なくしてどうして剰余が求まるのかと。言われてみれば当然のことだが、剰余加算器まで説明してくれている稀有なショアアリゴリズムの解説でさえも、そんな当たり前のことには言及されないようだ。
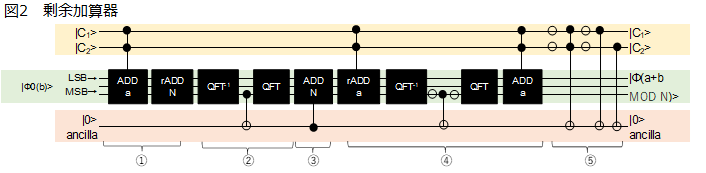
実は、重要なことは、a<N、b<Nである点。つまり、a+b<2Nである。この条件下で a+b<N であれば、割った余りは当然、a+b そのものとなる。例えば N=57、a+b=43 であれば、商は0で余りは 43 そのものである。一方、N<a+b<2N であったら? 例えば N=57、a+b=69 であれば、商は1で余りは 69-57 = 12 である。つまり、商が0か1のみ。故に足し算、引き算以外は必要ない。で、大事なことは a+b が N より大きか小さいか。前例の通り a+b<N であれば商は0で余りは a+b、後例の通り a+b>N であれば商は1で余りは a+b-N である。
図2の回路の説明をしよう。$|C_1>$と$|C_2>$は、後々の制御のためのビットで、ご覧の通り、これらが共に'1'の時のみ、φ(a+b MOD N) が計算される。図2の➀部分では、a+b が N より大きか小さいかに関係なく a+b-N を計算している。実はbは二進数でnビットだが、ここではMSB(最上位ビット)に初めから0が付加されている。先頭に0を付けても値は変わらないので。もし a+b<N であると a+b-N は負だが、実際には負にならず、オーバーフローしMSBは'1'となる。➁でこれを検出し制御NOTで補助ビット(ancilla)を'1'にする。➂でこの補助ビットが'1'であれば、つまり、a+b<Nであれば、+Nしa+bにしている。当然、a+b>Nであれば、MSBはゼロのまま、補助ビットもゼロのままのため➂は作用しないため、a+b-Nのままである。つまり計算的はここまで終了である。がしかし、補助ビットをきちんと初期化しておかなければならない。➃は先の結果から故意にaを引くことにより再度MSBがオーバーフローかどうかを判定している。もしa+b-N(つまりMSB='0',補助='0')であれば、b-Nで負となりオーバーフローとなりMSBは'1'となる。逆の場合(つまりMSB='1',補助='1')は結果bでありMSBはそのまま'0'である。これでは全くの逆のため、MSBを一旦フリップさせ、補助ビットを標的として制御NOTを行う。こうすれば、補助ビットはどちらの場合もゼロとなる。その後、MSBを再度フリップし元に戻し、さらに再びaを加算し結果を元に戻して終了・・・のはずが・・・ Beauregardの基の論文には出てこない故、独自でモディファイした部分となるが、$|C_1>$及び/又は$|C_2>$がゼロであると、図2のaに関する加減算は作用しないが、Nに関する加減算は作用してまう。引いて足しているので結果には影響しないが、MSBと補助ビットには影響がでてしまい、➃段階で補助ビットは'1'となってしまう。それを消すために➄を付加している。$|C_1>$、$|C_2>$共にゼロの場合では、反転後、トフォリゲートで標的を補助ビットとして消し、いずれか一方がゼロの場合は制御NOTで補助ビットを消すようにしている。
blueqatでの実装の前に、制御加算器や制御制御加算器が必要となるが、それをどのように作るのか?知りたければ以下の折りたたみの補足を参照されたし。
**【補足】制御制御回転ゲートの作り方**
さて、buleqatでの実装である。以下に剰余加算器の核心部分のコード記した。また、コードの中の丸数字でのコメントアウトは図2の丸数字部分と対応させている。登場する各モジュールは2-1と同じである。
# -------- c adder ---------------------------------------------------------------
def cadder(constx,cn1): #制御加算器
for i in range(N):
bi=N-i-1
for j in range(bi,-1,-1):
if constx[j]==1:
ang=(2*np.pi)/(2**(bi-j+1))
c.crz(ang)[cn1,bi]
return
# -------- cc adder ---------------------------------------------------------------
def ccadder(constx,cn1,cn2): #制御制御加算器
for i in range(N):
bi=N-i-1
for j in range(bi,-1,-1):
if constx[j]==1:
ang=(np.pi)/(2**(bi-j+1))
c.crz(ang)[cn2,bi].cx[cn1,cn2].crz(-ang)[cn2,bi]
c.cx[cn1,cn2].crz(ang)[cn1,bi]
return
# -------- cc reverse adder ------------------------------------------------------
def ccrevadder(constx,cn1,cn2): #制御制御減算器
for bi in range(N):
for j in range(bi+1):
if constx[j]==1:
ang=(-np.pi)/(2**(bi+1-j))
c.crz(ang)[cn2,bi].cx[cn1,cn2].crz(-ang)[cn2,bi]
c.cx[cn1,cn2].crz(ang)[cn1,bi]
return
# -------- mod adder ------------------------------------------------------------
def modadder(c1m,c2m,ancilm,const_am,const_Nm): #剰余加算モジュール
ccadder(const_am,c1m,c2m) #➀
ccrevadder(const_Nm,c1m,c2m) #➀
IQFT() #➁
swapN() #➁
c.cx[MSB,ancilm] #➁
QFT() #➁
swapN() #➁
cadder(const_Nm,ancilm) #➂
ccrevadder(const_am,c1m,c2m) #➃
IQFT() #➃
swapN() #➃
c.x[MSB].cx[MSB,ancilm].x[MSB] #➃
QFT() #➃
swapN() #➃
ccadder(const_am,c1m,c2m) #➃
c.x[c1m].x[c2m].ccx[c1m,c2m,ancilm].x[c1m].x[c2m] #➄
c.cx[c1m,ancilm].cx[c2m,ancilm] #➄
また、以下の折りたたみに実際に実行するプログラム全体を示した。その他諸々は2-1と同様である。
**qft-mod-adder.py(全体)**
# qft-mod-adder by Gigagulin 2021 Nov.
from blueqat import Circuit
import numpy as np
import qcam
# -------- Setting --------------------------------------------------------------
N=16
NT=N+3 # numaer of qubit
initial_a=np.array([0]*NT,dtype='int') # b
const=np.array([0]*(N),dtype='int') # a constant
cca=np.array([1,1,0],dtype='int')
C1,C2,ancillary=N,N+1,N+2
MSB=0
# -------- QFT ------------------------------------------------------------------
def QFT():
for i in range(N):
for j in range(i):
c.cu1(np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- inversed QFT ---------------------------------------------------------
def IQFT():
for i in range(N):
for j in range(i):
c.cu1(-np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- c adder ---------------------------------------------------------------
def cadder(constx,cn1): #制御加算器
for i in range(N):
bi=N-i-1
for j in range(bi,-1,-1):
if constx[j]==1:
ang=(2*np.pi)/(2**(bi-j+1))
c.crz(ang)[cn1,bi]
return
# -------- cc adder ---------------------------------------------------------------
def ccadder(constx,cn1,cn2): #制御制御加算器
for i in range(N):
bi=N-i-1
for j in range(bi,-1,-1):
if constx[j]==1:
ang=(np.pi)/(2**(bi-j+1))
c.crz(ang)[cn2,bi].cx[cn1,cn2].crz(-ang)[cn2,bi]
c.cx[cn1,cn2].crz(ang)[cn1,bi]
return
# -------- cc reverse adder ------------------------------------------------------
def ccrevadder(constx,cn1,cn2): #制御制御減算器
for bi in range(N):
for j in range(bi+1):
if constx[j]==1:
ang=(-np.pi)/(2**(bi+1-j))
c.crz(ang)[cn2,bi].cx[cn1,cn2].crz(-ang)[cn2,bi]
c.cx[cn1,cn2].crz(ang)[cn1,bi]
return
# -------- swap ------------------------------------------------------------------
def swapN():
Nh=int(N/2)
for i in range(Nh):
c.swap[i,N-i-1]
return
# -------- deci to bin ------------------------------------------------------------
def dtb(deci):
binlist=np.array([0]*N,dtype='int')
tempo1_list=list(bin(deci)) # vector extraction butreversed. (Decimal to Binary)
del tempo1_list[0:2] # Delete '0','b' in tempo list
tempo1_list[0:0]=['0']*(N-len(tempo1_list)) # Zero-fill to adjust digits
for i in range(N):
binlist[i]=tempo1_list[i]
return binlist
# -------- mod adder ------------------------------------------------------------
def modadder(c1m,c2m,ancilm,const_am,const_Nm): #剰余加算モジュール
ccadder(const_am,c1m,c2m) #➀
ccrevadder(const_Nm,c1m,c2m) #➀
IQFT() #➁
swapN() #➁
c.cx[MSB,ancilm] #➁
QFT() #➁
swapN() #➁
cadder(const_Nm,ancilm) #➂
ccrevadder(const_am,c1m,c2m) #➃
IQFT() #➃
swapN() #➃
c.x[MSB].cx[MSB,ancilm].x[MSB] #➃
QFT() #➃
swapN() #➃
ccadder(const_am,c1m,c2m) #➃
c.x[c1m].x[c2m].ccx[c1m,c2m,ancilm].x[c1m].x[c2m] #➄
c.cx[c1m,ancilm].cx[c2m,ancilm] #➄
return
# -------- Main aody --------------------------------------------------------------
c=Circuit(NT)
No=input(' N(const)=')
ao=input(' a(const)=')
bo=input(' b=')
tempo_N=dtb(int(No))
tempo_a=dtb(int(ao))
tempo_b=dtb(int(bo))
const_N = list(reversed(tempo_N))
const_a = list(reversed(tempo_a))
initial_a=np.append(tempo_b,cca)
qcam.propinit(NT,c,initial_a)
QFT()
swapN()
modadder(C1,C2,ancillary,const_a,const_N)
IQFT()
swapN()
master_a=np.array(c.run())
num,vector_a,prob_a=qcam.qvextract(NT,1,1,master_a)
stdev,probability_a=qcam.qcalcd(NT, num,vector_a,prob_a)
sum=0
for i in range(N):
sum=probability_a[N-i-1]*(2**i)+sum
print(' ',ao,'+',bo,' mod',No,' = ',int(np.round(sum,decimals= 0))
2-3.剰余乗算器
次に、2-2.の剰余加算器(別名 Beauregard加算器)を用いた剰余乗算器(cmultと略す)を説明しよう。ここで初めて1-1のショアアルゴリズムの超概観で示した式1に登場していたxが登場する。この剰余乗算器では、|x>と|φ(b)>を入力として、結果として|φ(b+ax MOD N)> を出す。図3に量子回路を示した。
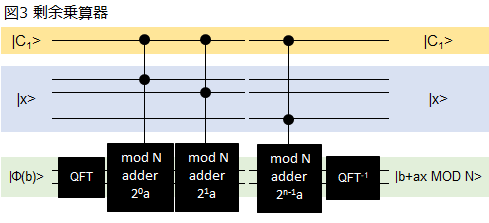
図3の回路の説明をしよう。$|C_1>$は、後の制御のためのビットである。登場するのは既に説明済みのQFTとIQFTと剰余加算器(図中では、mod N adder $2^ia$ で示している)のみである。2-2.の剰余加算器の$|C_2>$に桁ごとの|x>を入れている。また、定数aの部分は、$2^ia$を、これも定数として入れている。以上でここでの目的は達成される。例によって、核心部分のモジュールを示す?・・・って実のところ、核心部分は前の剰余加算器で、ここでは古典的な制御フローのみである。
QFT()
swapN()
for m in range(X):
C2=N+X-m-1 #C2の代わりのXのqubit番号
tempo_ax=dtb(a*(2**m),N) #aに2乗数をかける
const_ax = list(reversed(tempo_ax))
modadder(C1,C2,ancillary,const_ax,const_N) #2-2.剰余加算器モジュール
IQFT()
swapN()
また例によって、以下の折りたたみに実際に実行するプログラム全体を示した。その他諸々は2-1と同様である。残念なお知らせではあるがSKDでの計算時間など諸都合から b のqubit数を16から8に減らした。
**qft-cmult-mod.py(全体)**
# q-cmult-mod by Gigagulin 2021 Dec.
from blueqat import Circuit
import numpy as np
import qcam
# -------- Setting --------------------------------------------------------------
N=8
X=8
NT=N+X+2 # numaer of qubit
initial_a=np.array([0]*N,dtype='int') # b
cca=np.array([1,0],dtype='int')
C1,ancillary=N+X,N+X+1
MSB=0
const_ap=np.array([0]*X,dtype='int')
# -------- QFT ------------------------------------------------------------------
def QFT():
for i in range(N):
for j in range(i):
c.cu1(np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- inversed QFT ---------------------------------------------------------
def IQFT():
for i in range(N):
for j in range(i):
c.cu1(-np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- c adder ---------------------------------------------------------------
def cadder(constx,cn1):
for i in range(N):
bi=N-i-1
for j in range(bi,-1,-1):
if constx[j]==1:
ang=(2*np.pi)/(2**(bi-j+1))
c.crz(ang)[cn1,bi]
return
# -------- cc adder ---------------------------------------------------------------
def ccadder(constx,cn1,cn2):
for i in range(N):
bi=N-i-1
for j in range(bi,-1,-1):
if constx[j]==1:
ang=(np.pi)/(2**(bi-j+1))
c.crz(ang)[cn2,bi].cx[cn1,cn2].crz(-ang)[cn2,bi]
c.cx[cn1,cn2].crz(ang)[cn1,bi]
return
# -------- cc reverse adder ------------------------------------------------------
def ccrevadder(constx,cn1,cn2):
for bi in range(N):
for j in range(bi+1):
if constx[j]==1:
ang=(-np.pi)/(2**(bi+1-j))
c.crz(ang)[cn2,bi].cx[cn1,cn2].crz(-ang)[cn2,bi]
c.cx[cn1,cn2].crz(ang)[cn1,bi]
return
# -------- swap ------------------------------------------------------------------
def swapN():
Nh=int(N/2)
for i in range(Nh):
c.swap[i,N-i-1]
return
# -------- deci to bin ------------------------------------------------------------
def dtb(deci,noder):
binlist=np.array([0]*noder,dtype='int')
tempo1_list=list(bin(deci)) # vector extraction butreversed. (Decimal to Binary)
del tempo1_list[0:2] # Delete '0','b' in tempo list
tempo1_list[0:0]=['0']*(noder-len(tempo1_list)) # Zero-fill to adjust digits
for i in range(noder):
binlist[i]=tempo1_list[i]
return binlist
# -------- mod adder ------------------------------------------------------------
def modadder(c1m,c2m,ancilm,const_am,const_Nm):
ccadder(const_am,c1m,c2m)
ccrevadder(const_Nm,c1m,c2m)
IQFT()
swapN()
c.cx[MSB,ancilm]
QFT()
swapN()
cadder(const_Nm,ancilm)
ccrevadder(const_am,c1m,c2m)
IQFT()
swapN()
c.x[MSB].cx[MSB,ancilm].x[MSB]
QFT()
swapN()
ccadder(const_am,c1m,c2m)
c.x[c1m].x[c2m].ccx[c1m,c2m,ancilm].x[c1m].x[c2m] # modified
c.cx[c1m,ancilm].cx[c2m,ancilm]
return
# -------- Main aody --------------------------------------------------------------
c=Circuit(NT)
No=input(' N(const)=')
ao=input(' a(const)=')
bo=input(' b=')
xo=input(' x=')
tempo_N=dtb(int(No),N)
tempo_b=dtb(int(bo),N)
tempo_x=dtb(int(xo),X)
a=int(ao)
const_N = list(reversed(tempo_N))
tempo_bx=np.append(tempo_b,tempo_x)
initial_a=np.append(tempo_bx,cca)
qcam.propinit(NT,c,initial_a)
QFT()
swapN()
for m in range(X):
C2=N+X-m-1
tempo_ax=dtb(a*(2**m),N)
const_ax = list(reversed(tempo_ax))
modadder(C1,C2,ancillary,const_ax,const_N)
IQFT()
swapN()
master_a=np.array(c.run())
num,vector_a,prob_a=qcam.qvextract(NT,1,1,master_a)
stdev,probability_a=qcam.qcalcd(NT, num,vector_a,prob_a)
sum=0
for i in range(N):
sum=probability_a[N-i-1]*(2**i)+sum
print(' ',int(bo)+a*int(xo),' mod ',No,' = ',int(np.round(sum,decimals= 0)))
実際の実行結果例は以下の通りである。
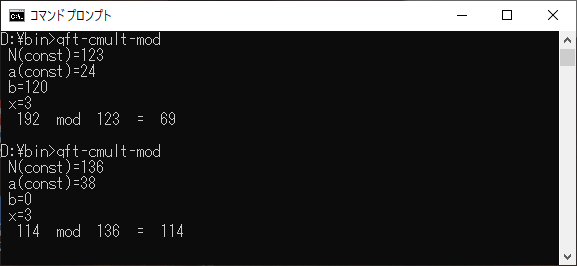
ここで、投稿者のような人間は早とちりで、|φ(b+ax MOD N)>でb=0なら|φ(ax MOD N)>である。現に上の実行結果でb=0にした時、ax MOD N が出ている。ここまでで完成ではと。
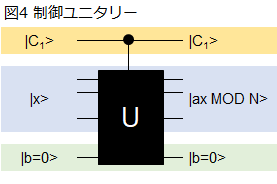
2-4.制御ユニタリー(べき余剰)
がそうはいかない。図3の回路図を再度見て欲しい。答えである|φ(b+ax MOD N)>が|φ(b)>のライン(図では薄緑色)に出てきている。1-1.の式1ではxに対する関数となっている。要は、図3の|x>のライン(図では薄青色)に |φ(b+ax MOD N)>が出てこなくてはならない。さもないと図4の左側のようなQPEに適用する制御ユニタリーとはならない。
では、図3の出側の|x>と|φ(b+ax MOD N)>をスワップすれば良いのではないかと浮かぶ。確かにそれで図4の薄青のラインは完成する。がしかし、薄緑の出側には新たに|x>が入ってしまう。今や0のbはancillaビットのようなものだ。QPEで次々とこのユニタリーを適用していくのであるから、一回 U を実行した後は bは再びゼロとなっていなければならない。では、どうする?
Beauregardの文献では、|x>と|φ(b+ax MOD N)>をスワップ後に、aではなくaの逆元である$a^{-1}$に2-3.の剰余乗算器($cmult$)の逆演算版($cmult^{-1}$)を適用することによりゼロ化している。以下にその過程を示した。一目瞭然だと思われる。
$$|x>|0>\\→{cmult(a)}→,|x>|(ax)mod N>\\→{swap}→,|(ax)mod N>|x>\\
→{cmult^{-1}(a^{−1})}→,|(ax)mod N>|(x − a^{−1}ax)mod N> \\= |(ax)mod N>|0>\qquad \qquad(式5)$$
ただし、ここでの$a^{-1}$(逆元)とは、Nを法としたモジュロ逆数と言われるものであり、拡張ユークリッド互助法あるいはオイラーの定理を利用して計算される。a,Nも古典定数のため古典計算で$a^{-1}$を求める。折角なのでqiitaにあった
@akebono-sanの記事拡張ユークリッドの互除法を非再帰で実装する(Python) のモジュールを紹介する。
def modinv(am, bm): # am=a bm=N(法)
pm = bm
xm, ym, um, vm = 1, 0, 0, 1
while bm:
km = am // bm
xm -= km * um
ym -= km * vm
xm, um = um, xm
ym, vm = vm, ym
am, bm = bm, am % bm
xm %= pm
if xm < 0:
xm += pm
return xm # xmがaの逆元
しかし、実は逆元を求めなおかつ逆演算版$cmult^{-1},(a^{-1})$を組むことは大変である。一応(一部不具合が含まれる)、前のcmultを以下の点で改造し組んでみた。
・cmultをモジュール化
・cmultのinverseであるinvcmultとmod adderの逆演算revmodadderを追加
・swapは全て制御swapに置き換え。制御でs1,s2を入れ替えるコード cx[s1,s2].ccx[ctrl,s1,s2].cx[s1,s2]
・b=0は確定しているので、bの入力は消した
これら改造をしたプログラムを以下の折りたたみに記した。
**べき余剰のユニタリーゲート全体**
# q-CU by Gigagulin 2021 Dec.
from blueqat import Circuit
import numpy as np
import qcam
import time
# -------- Setting --------------------------------------------------------------
N=8
X=8
n_counter=1
NX=N+X
NT=NX+n_counter+1 # numaer of qubit
initial_b=np.array([0]*N,dtype='int') # b
cca=np.array([1,0],dtype='int')
C1,ancillary=N+X,N+X+1
MSB=0
const_ap=np.array([0]*X,dtype='int')
# -------- QFT ------------------------------------------------------------------
def QFT():
for i in range(N):
for j in range(i):
c.cu1(np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- inversed QFT ---------------------------------------------------------
def IQFT():
for i in range(N):
for j in range(i):
c.cu1(-np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- c adder ---------------------------------------------------------------
def cadder(constx,cn1):
for i in range(N):
bi=N-i-1
for j in range(bi,-1,-1):
if constx[j]==1:
ang=(2*np.pi)/(2**(bi-j+1))
c.crz(ang)[cn1,bi]
return
# -------- cc adder ---------------------------------------------------------------
def ccadder(constx,cn1,cn2):
for i in range(N):
bi=N-i-1
for j in range(bi,-1,-1):
if constx[j]==1:
ang=(np.pi)/(2**(bi-j+1))
c.crz(ang)[cn2,bi].cx[cn1,cn2].crz(-ang)[cn2,bi]
c.cx[cn1,cn2].crz(ang)[cn1,bi]
return
# -------- c reverse adder ---------------------------------------------------------------
def crevadder(constx,cn1):
for bi in range(N):
for j in range(bi+1):
if constx[j]==1:
ang=(-2*np.pi)/(2**(bi+1-j))
c.crz(ang)[cn1,bi]
return
# -------- cc reverse adder ------------------------------------------------------
def ccrevadder(constx,cn1,cn2):
for bi in range(N):
for j in range(bi+1):
if constx[j]==1:
ang=(-np.pi)/(2**(bi+1-j))
c.crz(ang)[cn2,bi].cx[cn1,cn2].crz(-ang)[cn2,bi]
c.cx[cn1,cn2].crz(ang)[cn1,bi]
return
# -------- swap1 ------------------------------------------------------------------
def swapN(nk,c1x):
Nh=int(nk/2)
for i in range(Nh):
c.cx[i,nk-i-1].ccx[c1x,nk-i-1,i].cx[i,nk-i-1]
return
# -------- swap2 ------------------------------------------------------------------
def swapX(nk,c1x):
Nh=int(nk/2)
for i in range(Nh):
c.cx[N+i,N+nk-i-1].ccx[c1x,N+nk-i-1,N+i].cx[N+i,N+nk-i-1]
return
# -------- deci to bin ------------------------------------------------------------
def dtb(deci,noder):
binlist=np.array([0]*noder,dtype='int')
tempo1_list=list(bin(deci)) # vector extraction butreversed. (Decimal to Binary)
del tempo1_list[0:2] # Delete '0','b' in tempo list
tempo1_list[0:0]=['0']*(noder-len(tempo1_list)) # Zero-fill to adjust digits
for i in range(noder):
binlist[i]=tempo1_list[i]
return binlist
# -------- mod adder ------------------------------------------------------------
def modadder(c1m,c2m,ancilm,const_am,const_Nm):
ccadder(const_am,c1m,c2m)
ccrevadder(const_Nm,c1m,c2m)
IQFT()
swapN(N,C1)
c.cx[MSB,ancilm]
QFT()
swapN(N,C1)
cadder(const_Nm,ancilm)
ccrevadder(const_am,c1m,c2m)
IQFT()
swapN(N,C1)
c.x[MSB].cx[MSB,ancilm].x[MSB]
QFT()
swapN(N,C1)
ccadder(const_am,c1m,c2m)
c.x[c1m].x[c2m].ccx[c1m,c2m,ancilm].x[c1m].x[c2m] # modified
c.cx[c1m,ancilm].cx[c2m,ancilm]
return
# -------- reverse mod adder ------------------------------------------------------------
def revmodadder(c1m,c2m,ancilm,const_am,const_Nm):
c.cx[c1m,ancilm].cx[c2m,ancilm]
c.x[c1m].x[c2m].ccx[c1m,c2m,ancilm].x[c1m].x[c2m]
ccrevadder(const_am,c1m,c2m)
IQFT()
swapN(N,C1)
c.x[MSB].cx[MSB,ancilm].x[MSB]
QFT()
swapN(N,C1)
ccadder(const_am,c1m,c2m)
crevadder(const_Nm,ancilm)
IQFT()
swapN(N,C1)
c.cx[MSB,ancilm]
QFT()
swapN(N,C1)
ccadder(const_Nm,c1m,c2m)
ccrevadder(const_am,c1m,c2m)
return
# ------- modinv ---------------------------------------------------------------------
def modinv(am, bm):
pm = bm
xm, ym, um, vm = 1, 0, 0, 1
while bm:
km = am // bm
xm -= km * um
ym -= km * vm
xm, um = um, xm
ym, vm = vm, ym
am, bm = bm, am % bm
xm %= pm
if xm < 0:
xm += pm
return xm
# ------- cmult ---------------------------------------------------------------------
def cmult(ac):
QFT()
swapN(N,C1)
for m in range(X):
C2=N+X-m-1
tempo_ax=dtb(ac*(2**m),X)
const_ax = list(reversed(tempo_ax))
modadder(C1,C2,ancillary,const_ax,const_N)
IQFT()
swapN(N,C1)
return
# ------- inversed cmult ---------------------------------------------------------------------
def invcmult(ac):
QFT()
swapN(N,C1)
for m in range(X):
C2=N+X-m-1
tempo_ax=dtb(ac*(2**m),X)
const_ax = list(reversed(tempo_ax))
revmodadder(C1,C2,ancillary,const_ax,const_N)
IQFT()
swapN(N,C1)
return
# -------- Main aody --------------------------------------------------------------
c=Circuit(NT)
No=input(' N(const)=')
ao=input(' a(const)=')
xo=input(' x=')
tempo_N=dtb(int(No),N)
tempo_x=dtb(int(xo),X)
a=int(ao)
const_N = list(reversed(tempo_N))
tempo_bx=np.append(initial_b,tempo_x)
initial_a=np.append(tempo_bx,cca)
qcam.propinit(NT,c,initial_a)
cmult(a)
swapN(N+X,C1)
swapN(N,C1)
swapX(X,C1)
ainv=modinv(a, int(No))
invcmult(ainv)
t0=time.time()
master_a=np.array(c.run())
t1=time.time()
num,vector_a,prob_a=qcam.qvextract(NT,1,1,master_a)
stdev,probability_a=qcam.qcalcd(NT, num,vector_a,prob_a)
print(' Quantum Process Time =>',t1-t0)
sum=0
for i in range(X):
sum=probability_a[N+X-i-1]*(2**i)+sum
print('mod=',int(np.round(sum,decimals= 0)))
sum=0
for i in range(N):
sum=probability_a[N-i-1]*(2**i)+sum
print('green=',int(np.round(sum,decimals= 0)))
念のために上記、折りたたみ内のプログラムでは、’green'で薄緑色のレジスタがゼロになっていることを確認できるようにしている。また、シミュレーターでの計算時間も示した。
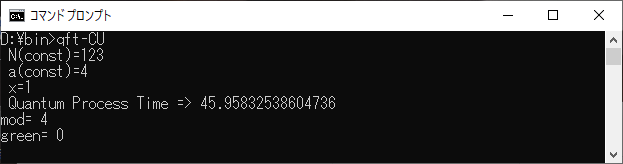
制御ユニタリーができたので、すわ!QPEで位数発見といきたいが、しかし、これ以上先に進むには困難があった。
・不具合上の問題(現時点で修正中)でこのままQPEを適用しても正しい答えが得られないだろう
・計算時間がかかる
・なにより、8ビットしかなく、MSB除くと実質的には127までしか適用できない
などの大人の都合が続出してしまう・・・そこで、別法の登場となる。
3. 別法では予め位数が分かっていなければならない件
3-1.別法
複雑なべき余剰をさけた別法でショアアルゴリズムの解説をしている記事によく出くわす。前述までの通りべき余剰を突き進めるより賢明と思うが、一方でこの方法では肝心の位数発見の量子アルゴリズムに位数が分かっていなければならいというナンセンスな前提がある。素人の私が勘違いしているのかもしれない。むしろそうであればよいのだが。で、この別法の量子回路を図5に示した。
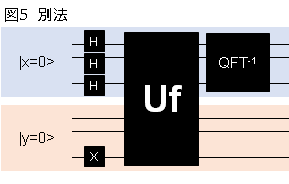
非常にシンプルである。ポイントは図のUfの部分。ここに
$$f(x)=a^x,mod,N\quad (x=0,1,2,...)\qquad(式1)$$
このxの関数を入れるのではなく、xの数値に応じた式1から計算された剰余の結果そのものをプラグラム(オラクル)として落とし込むのである。剰余はx=r(位数)での周期をもっており、0から位数までの剰余すべてをオラクルに入れるのである。
1-2.で示した、世間によくある例、N=15,a=7で具体的に説明しよう。x=0,1,2,3,4,・・・での余りは、y=1,7,4,13,1,・・・である。この段階で位数が4であることが分かる。このxとyを以下の表に示した。表の左側は十進表記で、右側はそれを二進数化したものである。
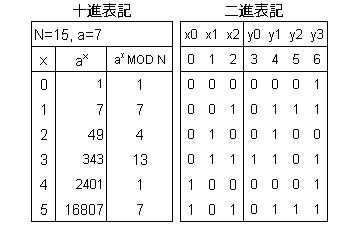
はじめにyのLSBを反転させ初期状態を0001とする。このX側のqubitを制御ビットにして、y側の各qubitを標的にした制御NOTゲートを駆使して余りである'0'と'1'の組合わせを作り出す力技を行う。そのプロセスを以下の折りたたみ内に表として示した。
**プロセス**
このプロセスをblueqatのコードで記せば、c.cx[2,4].cx[2,5].cx[1,4].cx[1,6].ccx[1,2,3].ccx[1,2,4].ccx[1,2,5].ccx[1,2,6]である。これをプラグラムに仕上げたものが以下の折りたたみである。プログラムの委細に関しては量子位相推定をグローバーやセルオートマトンに適用してみたを参照されたし。
**別法15**
# q-shor15 by Gigagulin
from blueqat import Circuit
import numpy as np
import qcam
from fractions import Fraction
# -------- Setting ------------------------------------------------------------------
xbit,ybit=3,4
N=xbit+ybit
initial_a=np.array([0.5,0.5,0.5,0,0,0,1],dtype='float') # initial set
# -------- inversed QFT ------------------------------------------------------------------
def IQFT():
for i in range(xbit):
for j in range(i):
c.cu1(-np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- Q-Process -----------------------------------------------------------------------
def qproc():
c.cx[2,4].cx[2,5].cx[1,4].cx[1,6]
c.ccx[1,2,3].ccx[1,2,4].ccx[1,2,5].ccx[1,2,6]
return
# -------- Main Body --------------------------------------------------------------
c=Circuit(N)
qcam.propinit(N,c,initial_a)
qproc()
IQFT()
master_a=np.array(c.run())
num,vector_a,prob_a=qcam.qvextract(N,1,1,master_a)
print('ybin ydeci xbin xdeci probability phase guess')
for j in range(num):
xdeci,ydeci=0,0
print('b',end='')
for i in range(xbit,N):
print(vector_a[j,i],end='')
ydeci=int(vector_a[j,i])*2**(N-1-i)+ydeci
print(' ','{:>5}'.format(ydeci),' ',end=' ')
print('b',end='')
for i in range(xbit,):
print(vector_a[j,i],end='')
xdeci=int(vector_a[j,i])*2**i+xdeci
phase1=xdeci/(2**xbit)
guess1=str(Fraction(phase1).limit_denominator(10))
print(' ','{:>5}'.format(xdeci),' ','{:>5,.4f}'.format(prob_a[j]),end=' ')
print(' ','{:>5,.4f}'.format(phase1),end=' ')
spa=' '*(6-len(guess1))
print(spa,':'+str(guess1))
実行結果は?
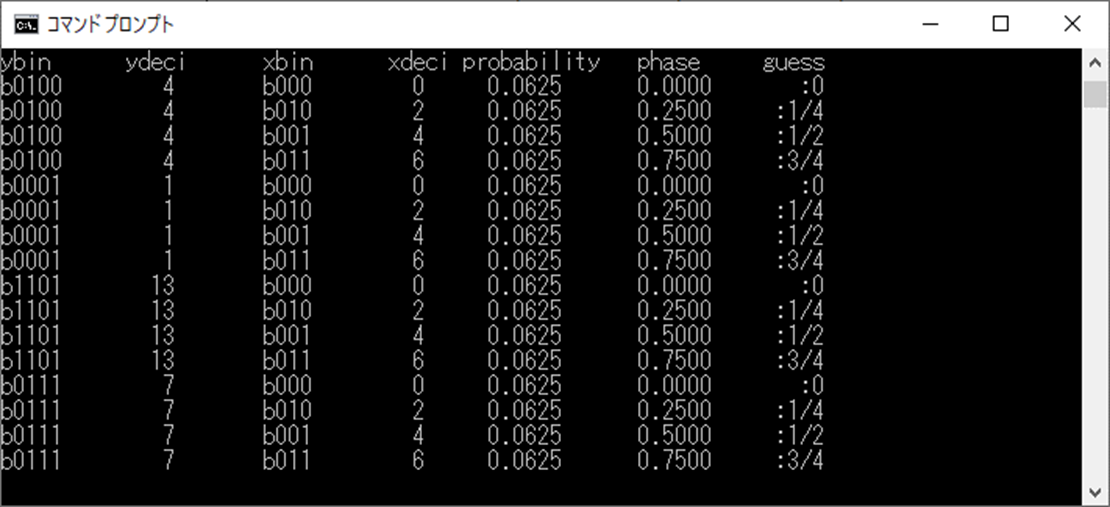
guessを御覧の通り、ゼロを無視すると1/4と3/4が確率的メジャーで、周期つまり位数は4であることが分かる・・・って初めから位数4て分かってたけど!
3-2.そしてN=約1憶の素因数分解
1億近くなれば素因数分解もすぐには暗算できないであろう。しかし、この別法を用いれば「1-2.Nの好例」であげた最大数である97180163ですら、いとも容易く解けることを示そう。任意の整数aを9858 と直感で定めよう。古典計算で以下の表の結果を得よう。位数は2である。
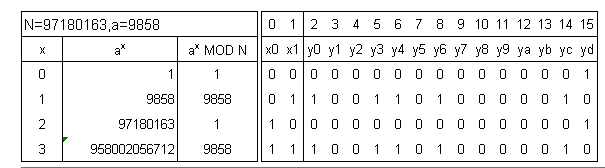
位数2なら、オラクルに簡単に落とし込める。x1が'1'のときyが9858の二進数相当の'1'と'0'の組み合わせになるようにゲートを組めば良いわけだ。それって制御ビットをx1にして、yで'1'となっている量子ビット番号を標的とした制御NOTをすればよいだけ?その通~り。一発でコードは書けて
c.cx[1,2].cx[1,5].cx[1,6].cx[1,8].cx[1,14].cx[1,15]
念の為、折りたたみに全体を記す。
**別法97180163**
# q-shor 97180163 by Gigagulin
from blueqat import Circuit
import numpy as np
import qcam
from fractions import Fraction
# -------- Setting ------------------------------------------------------------------
xbit,ybit=2,14
N=xbit+ybit
initial_a=np.array([0.5,0.5,0,0,0,0,0,0,0,0,0,0,0,0,0,1],dtype='float') # initial set
# -------- inversed QFT ------------------------------------------------------------------
def IQFT():
for i in range(xbit):
for j in range(i):
c.cu1(-np.pi/(2**(i-j)))[i,j]
c.h[i]
return
# -------- Q-Process -----------------------------------------------------------------------
def qproc():
c.cx[1,2].cx[1,5].cx[1,6].cx[1,8].cx[1,14].cx[1,15]
return
# -------- Main Body --------------------------------------------------------------
c=Circuit(N)
qcam.propinit(N,c,initial_a)
qproc()
IQFT()
master_a=np.array(c.run())
num,vector_a,prob_a=qcam.qvextract(N,1,1,master_a)
print(' ybin ydeci xbin xdeci probability phase guess')
for j in range(num):
xdeci,ydeci=0,0
print('b',end='')
for i in range(xbit,N):
print(vector_a[j,i],end='')
ydeci=int(vector_a[j,i])*2**(N-1-i)+ydeci
print(' ','{:>5}'.format(ydeci),' ',end=' ')
print('b',end='')
for i in range(xbit,):
print(vector_a[j,i],end='')
xdeci=int(vector_a[j,i])*2**i+xdeci
phase1=xdeci/(2**xbit)
guess1=str(Fraction(phase1).limit_denominator(10))
print(' ','{:>5}'.format(xdeci),' ','{:>5,.4f}'.format(prob_a[j]),end=' ')
print(' ','{:>5,.4f}'.format(phase1),end=' ')
spa=' '*(6-len(guess1))
print(spa,':'+str(guess1))
いざ実行。結果は以下の通り。

この結果から位数は2であることが分かる!だとすれば、式2から97180163の素因数分解は、9857 × 9859 と分かる。目出度し、目出度し!
おわりに
結局、多難の始まりは量子ビット数からくる制約である。がITの巨人達は2030年までに量子ビット百万等と言っている。その暁には2048ビット長のRSAは使い物にならなくなるのかも知れない。たかだか数年後である。その時のアドベントカレンダーでは何が語られているのであろうか?
-
先月、2021年11月にIBMが127qubitのイーグルQPUをリリースし、SDKのビット数より多きくなった。 ↩