はじめに
現代制御理論をはじめとするモデルに基づいたコントローラー開発では、制御対象の数学モデルが必要になります。
(総称としてモデルベースト制御(MBC : Model Based Control)と呼ばれます)
一般に数学モデルと言えば、伝達関数や数式で記述された常微分方程式(ODE)が主な表現形式ですが、中には明確な式表現が難しい、または分からないケースが多々あります。
例えば、温度や圧力、化学反応による反応物の濃度変化などの現象は、その動特性を表現した数式モデルが明示的に得られていないケースが多く、かつ非線形特性が強い対象です。
こうした明示的な数式モデルの構築が困難な対象は、入出力データを使ってモデルをブラックボックスで推定する、いわゆるシステム同定(System Identification)というデータドリブンなモデリングアプローチを検討することが可能です。
ここでプラントモデリングには、下図のように3つのアプローチが存在します。
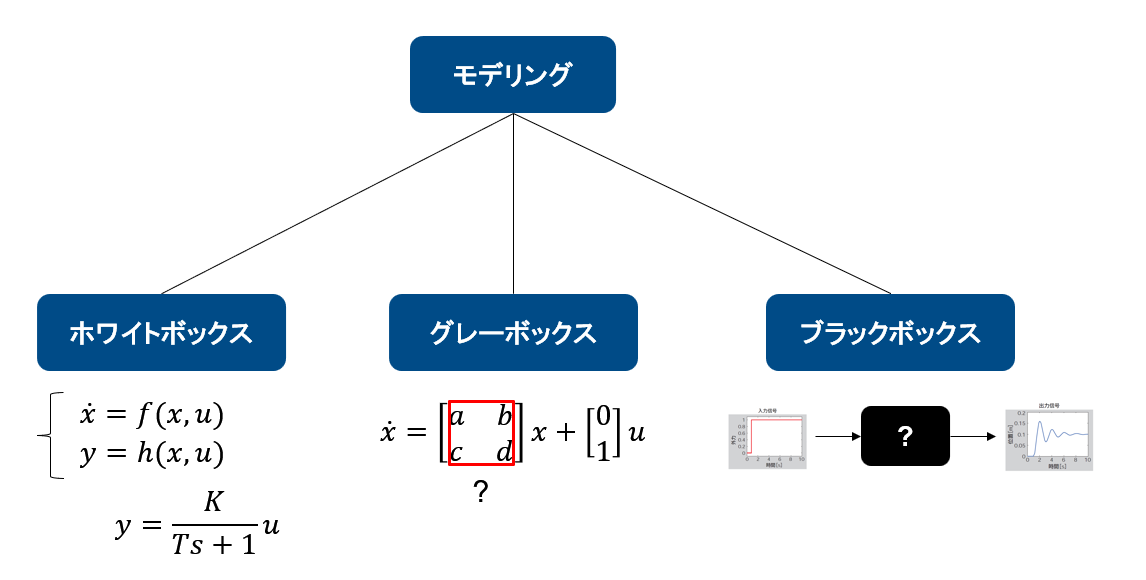
ホワイトボックスモデリング:
別名第一原理モデリングは対象を表す物理式等をベースに明示的に記述されるモデリングスタイル
ブラックボックスモデリング:
システム同定や低次元化モデル(ROM)、サロゲートモデルなどデータに基づいて、未知なモデルを同定/推定するモデリングスタイル
グレーボックスモデリング:
ホワイトボックスモデリングとブラックボックスモデリングの中間にあるモデリングスタイル
例えば、対象の物理式や構造が自明である一方で、それを構成する要素(パラメーター変数など)が未知の場合、データからパラメーター推定するといった場合はこれに当たる
今回はシステム同定に基づくブラックボックスモデリングをトピックに掲げて、どのようにコントローラー開発まで繋げていくのかをやってみたいと思います。
データドリブンなモデリング ~システム同定~
今回対象とするのは住宅の暖房システムです。
MATLABの製品ファミリーで物理モデリングを行うためのツール”Simscape”から提供されている以下の例題をベースにして設計を進めていきます。
本例題のモデルでは、住宅の室内環境モデルとして室内空間、壁、窓、および屋根の熱容量を考慮し、ヒーターからの熱供給及び外気との間で熱対流、熱伝導による熱交換を伴う構成となっています。

今回は、このモデルを実機と仮定し、かつ暖房システムが下図に示すようにPID制御によるシステムとして構成されており、室内温度(出力)、外気温度(外乱)、そしてヒーターからの入熱(制御入力)の各運転データが取得できるとします。

下図が取得した運転データの一部です。

上段から室内温度、外気温度、ヒーター入力と並んでいます。
外気温は見ての通り、正弦波状の温度変化を想定しています。
室内温度はPIDで制御された結果となりますが、オーバーシュートを伴う少々振動的な結果です。
これをシステム同定のための学習データとして使っていきます。
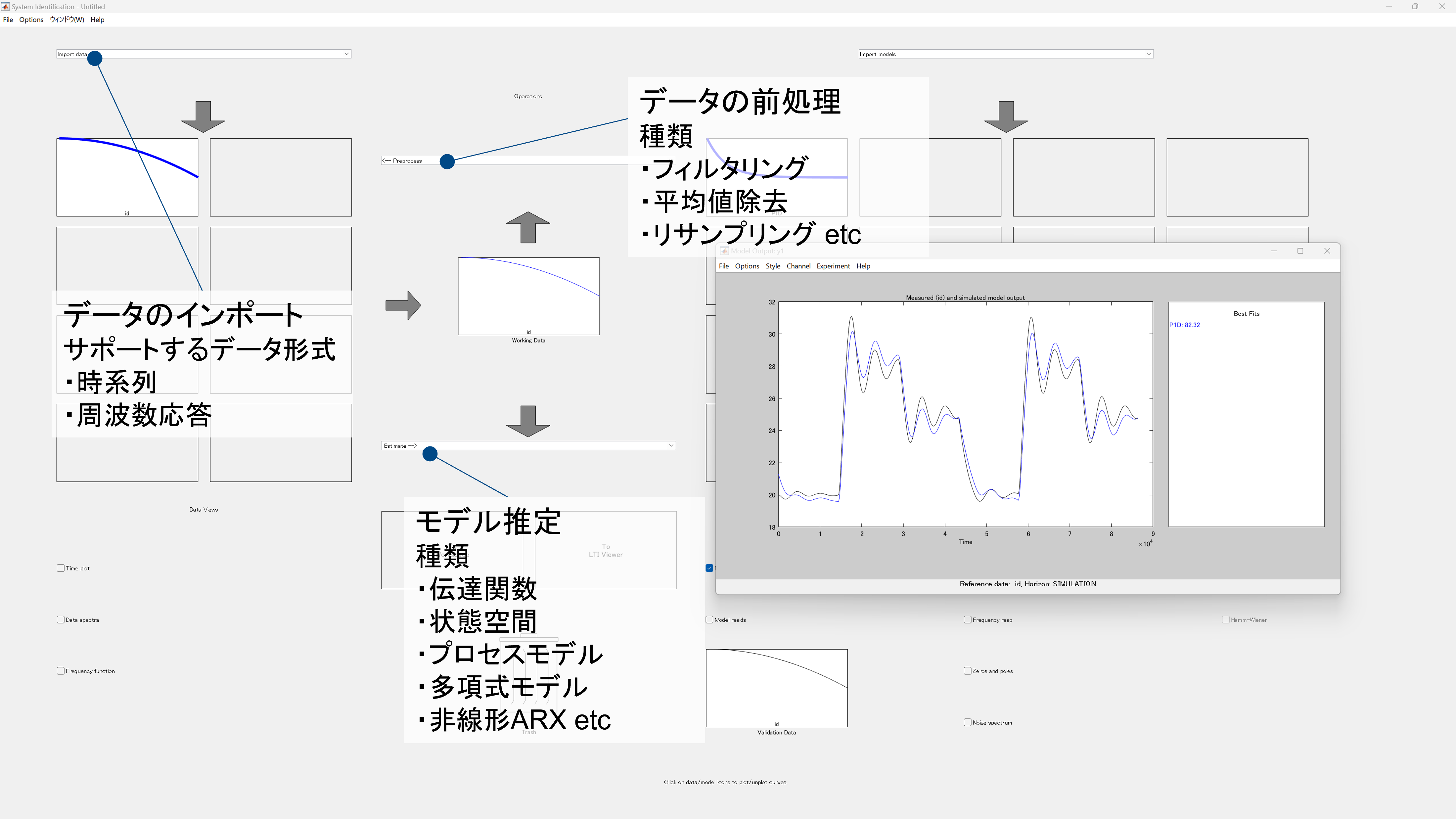
システム同定では主に下図に示す4つの工程で進められます。

ここで、大事なのはデータ取りです。
システム同定などいわゆるデータドリブンなアプローチはデータの質及び量が出力の精度に直結します。
対象の見極めをしっかりと行い、再現したいと考えている特性が十分に励起される試験信号の選定やデータ取得が行われることが肝要です。
またデータも一つの運転パターンではなく、可能な限り多くのパターンでバリエーションを多く含んだデータであることが大切です。
さて、システム同定を行うためのツールとしてMATLABからSystem Identification Toolboxが展開されていますので、今回はこれを使っていきます。
本ツールではGUIによる操作の他、コマンドによるプログラミングもできるのでユーザーが得意なやり方でシステム同定に取り組むことができます。
今回はコマンドを使用して処理を進めていきたいと思います。
先ほど貼付した室内温度のグラフを見ると、横軸時間に対して非常にゆっくりとした波形変化であることに気づくと思います。
一般に、温度のようなプロセス値は、時定数が大きく比較的ゆっくりとしたトレンド傾向になることが多いので、この場合は時定数、ゲイン、むだ時間で構成される下記プロセスモデル表現にて十分な精度を確保できるケースが多いです。
y(s) = \frac{K}{Ts+1} e^{-Ls}u(s)
それでは、同定モデルのタイプをプロセスモデルとして、先ほどの入出力の運転データからシステム同定を行ってみます。
なお、今回のデータは1秒周期で収録された時系列データです。
Ts = 1; % データの収録周期
id = iddata(y,[u1 u2],T); % y:室内温度、u1:ヒーター入力、u2:外気温度
sys = procest(id,"P1D"); % プロセスモデルとして推定
compare(id,sys) % データの比較
まず同定を行う前にiddataコマンドを使って、専用のデータオブジェクトを作ります。
今回は2入力(一つは制御入力、一つは外乱)のモデルですので、各々の時系列データを列ベクトルとしてマージして入力データを与えるようにしています。
なお、上記は1つのデータを使用してモデルを同定する際のデータの与え方になりますが、複数の運転データを使って同定を行うことも可能です。
詳細は↓のヘルプにて。
今回は省略していますが、データ準備の段階でデータのクレンジング(前処理)が必要になることもあります。
センサから取得したデータにはノイズが重畳されるケースが多く、ノイズが大きいと本来見たい出力が搔き消されてしまったり、また同定の際にノイズ成分も学習してしまうので精度が上がらないといった問題につながる場合もあります。
他にもデータの欠損が生じている可能性もあるので、必要に応じて補間やフィルタリング等を行ってデータをきれいにしてあげることが必要です。
データの準備ができたら、続いて同定用のコマンドにiddataオブジェクトと調整のためのオプション指定を与えると計算を行うことが出来ます。
今回はプロセスモデルのための同定コマンドであるprocestを使用します。
procestでは、引数の一つであるtypeプロパティにモデルの表現形式を文字列として与えます。
例として’P1D’と与える場合、一つの極とむだ時間を有するプロセスモデルとして同定を行うことになります。
詳細は以下のヘルプにて。
さて、同定によってモデルは以下の通りとなりました。

それぞれ、$u1~y$、$u2~y$までのプロセスモデルが計算されていることが分かります。
特に時定数がかなり大きい値であるため、非常に緩慢なダイナミクスを有していることが分かります。
またヒーター入力$u1$から室内温度$y$までには約90秒の大きなむだ時間もあることが分かります。
このことから、かなり制御がしづらい系であると考えることが出来ます。
procestで得られたモデルについて、学習データに対する精度をcompareコマンドで評価してみます。

上図がcompareコマンドによって得られたトレンドの比較図になりますが、確認すると灰色線の学習データに対し青線で示す同定モデルの出力はそこそこに合っていることが分かります。
凡例には定量的な評価指標であるFit率が表示されていますが、80.52%ということで悪くない数値です。
なお、Fit率の計算はNRMSE(Normalized Root Mean Square Error)に基づいています。
(詳細はcompareコマンドのヘルプを確認してください)
続いて、下図は学習とは別に用意したバリデーション(検証)用のデータを用いて、同定モデルの応答をcompareコマンドにより評価した結果となります。

トレンドを見るとそこそこに出力が合っていることが分かり、Fit率も70%以上あるので、汎化性を有していると結論づけることができます。
システム同定では、学習に使用したデータセット以外のセットを用いてバリデーション(検証)を行うことが大切です。
何故なら、得られたモデルが学習データに過適合(オーバーフィッティング)していた場合、その他のデータを与えた時に精度が著しく劣化する傾向にあるためです。
一般に、同定されたモデルに様々な入力データを与えた際にその出力が再現される能力を汎化性と呼びますが、過適合したモデルは、この汎化性が無いので学習データ以外については、信用に値しないモデルとなっています。
なお、何気なく行った今回のシステム同定、実は閉ループ同定$^{[1]}$と呼ばれるものになります。
一般に、システム同定は開ループの入出力データを用いた同定が行われることが多いです。
というのも、システム同定は下図のように入力$u$と出力に重畳される雑音$d$とがそれぞれ互いに無相関であることを前提にしているため、出力のフィードバックを有する閉ループ同定では、入力$u$に雑音$d$の影響が多少なりとも混入してしまうため、無相関という前提条件が崩れてしまいます。

そのため、閉ループ同定では入出力に無相関な信号、例えば目標信号$r1$や外乱$r2$を適切に振ってあげることでシステムの特性を励起し、同定を行うことが必要になります。
閉ループ同定については過去に詳細な記事を上げている方がいるのでとても参考になります。
他にも日本学術振興会 プロセスシステム工学第143委員会のワークショップ資料も大変参考になります。
モデル予測制御による温度制御系の設計
前の章にて制御対象の同定されたモデルが用意できたので、これを利用してコントローラーの設計を行っていきます。
今回は、MBCの中でも代表的かつ昨今注目を集めている制御手法として、モデル予測制御(MPC)を用いて制御系を設計していきたいと思います。
MPCと言えば、近年では車のドリフト制御や再利用ロケットの着陸制御技術なんかにも使われていると噂の先進的な制御手法です。
起源自体は1970年代頃と古くからある制御ですが、工場や化学プラント等のプロセス制御から発展してきて、近年は自動運転やロボット制御など幅広いアプリケーションへの展開が期待されています。
過去の記事でMPCを扱ったトピックをいくつか紹介していますので興味ある方はこちらもどうぞ。
今回は、同定モデルを用いて、線形なシステムを対象としたMPCコントローラーをModel Predictive Control Toolboxを利用して設計していきます。
その際、制御周期は10[s]、予測ホライズンは60ステップとして設定します。
MPCは、同定モデルを予測モデルとして用いて、10分(=600秒)先までの応答を毎制御周期で予測しつつ、実時間で最適化問題を解いていきます。
ts = 10; % 制御周期
p = 60; % 予測ホライズン
c = 2; % 制御ホライズン
sys = setmpcsignals(sys,'MV',1,'MD',2,'MO',1); % 信号プロパティの割り付け
mpcObj = mpc(sys,ts,p,c); % mpcコマンドに同定したモデル'sys'を与えている
mpcObj.ManipulatedVariables.Max = 1e4; % 入力上限[W]
mpcObj.ManipulatedVariables.Min = 0; % 入力下限[W]
mpcObj.Weights.OutputVariables = 1000; % 評価関数の出力に対する重み
mpcObj.Weights.ManipulatedVariables = 10; % 評価関数の入力に対する重み
mpcObj.ManipulatedVariables.ScaleFactor = 1e4; % 以下スケーリング係数(評価関数の正規化用)
mpcObj.DisturbanceVariables.ScaleFactor = 20;
mpcObj.OutputVariables.ScaleFactor = 30;
シミュレーション
前の章で設計したMPCコントローラーをプラントモデルと下図のように結合し、任意の温度目標値に対するMPCによる温度制御のシミュレーションを行います。
なお、プラントモデルや外気温度は、冒頭のものと同一であるとします。

下図がシミュレーション結果です。

結果を見て分かる通り、室内温度は目標温度に良好に追従していることが分かります。
特筆すべき点は、外気温度がかなり大きく変動しているにも関わらず、MPCはその影響を低く抑え込んでいます。
またヒーター入力を見てみると外気温度の変動カーブに合わせて入力を適切に変化させている様子が分かります。
冒頭のPID制御による応答の様子と比較すると、MPCによるヒーター制御システムはエネルギーロスが少なく、従来比較でかなり良い制御であると評価することが出来ます。
これが実機であれば、省エネ運転など環境への貢献が期待できそうです。
最後に
今回はシステム同定を使ったデータに基づく制御対象のモデリング、そして制御系設計を行うまでの1つのワークフローを試行してみました。
例題で示した通りシステム同定などのデータドリブンなアプローチは、対象の数式化が困難なシステムに対しその真価を発揮します。
非常に便利なアプローチですが、その反面難しさもあることを念頭に取り組まなければなりません。
データドリブンなアプローチは何といってもデータが命です。
データの量や質がモデルの精度に直結してくるため、如何に適切かつ適量なデータを収集できるかが鍵となってくるのは間違いありません。
参考文献
[1]足立 修一著:システム同定の基礎, 東京電機大学出版局