はじめに
今回は確率計画法に挑戦してみたいと思います。
確率計画法は、最適化問題に確率的要素（リスク）を含んだ数理計画法の一種です。
例えば、会社の商品に関して、不確かな市場の需要に基づきどれくらい製造したら良いのかを意思決定するといった問題が該当します。
確率計画法は問題に確率要素を含むため、普通に解くことができません。
そのため、一般に確率要素を確定要素に変換した上で解くというアプローチを検討します。
今回はその中でも2段階確率計画問題（Two-stage stochastic programming problem）を導入し、不確実性を含んだ最適化問題がどんな風に解けるのかを簡単な例題を通じて体験してみたいと思います。
電源投資に関する2段階確率計画問題
例題として、電力会社の電源投資を考えてみたいと思います。
シナリオは以下の通りです。
とある地域において、将来の電力需要が700, 1000, 1200, 1500 [MW]の間で取りうると想定され、かつ実際に生じる確率としてそれぞれ、10%, 20%, 40%, 30%と見積もられている。
現在、電力会社はこの地域の系統に2基の発電機（火力）を備えており、それぞれ以下のスペックとなっている。
・油火力
最大出力：400[MW]
発電コスト：1（正規化された値）
・LNG火力
最大出力：500[MW]
発電コスト：1.2（対油火力）
上記2基に加えて新たな電源として、需要のベースロードを担うために以下の2通りのスペックの発電所の建設を計画している。
・案1
最大出力：700[MW]
建設コスト：100
発電コスト：0.6（対油火力）
・案2
最大出力：1000[MW]
建設コスト：400
発電コスト：0.4（対油火力）
電力会社は、不確実な将来の電力需要に備えつつ、コストを最小限に抑えるため、どちらの案で電源を新設し、運用すべきだろうか。
以上が今回のお題目となります。
確率計画問題の定式化
今回の問題は、以下の通りどちらのスペック案の発電所を建設するかを需要が実現する前に決定する1段階と、確定した需要の下で最も発電コストの低い発電パターンを決定するという2段階から成る最適化問題の構成となっています。
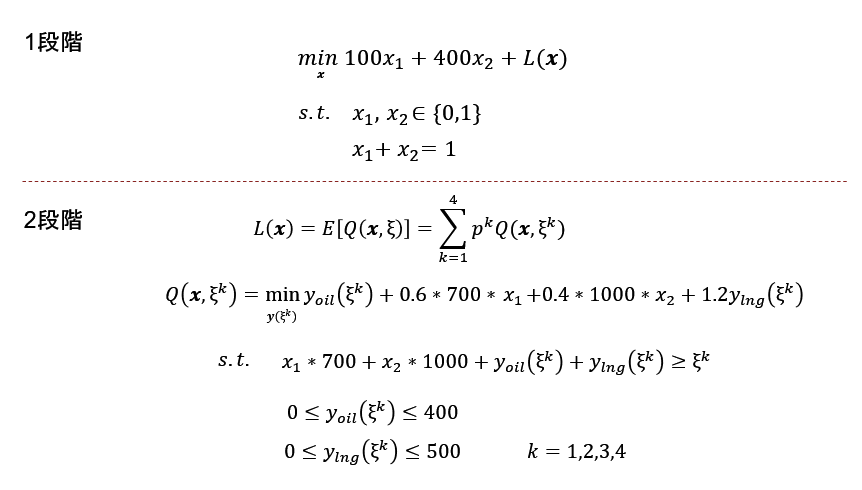ここで、$x_1$および$x_2$は案1、2に対応する整数変数であり、どちらかの案しか採択できません。電力需要は{$ξ^1$, $ξ^2$, $ξ^3$, $ξ^4$}={700, 1000, 1200, 1600}とし、その発生確率{$p^1$, $p^2$, $p^3$, $p^4$} = {10%, 20%, 40%, 30%}で表します。また各発電出力は$y_{**}$という変数で与えます。
1段階目の評価関数において、$L$はリコース関数と呼ばれるものです。リコースとは、金融における償還請求（債権者の債務者に対する遡った費用の返還請求権）を意味し、2段階目の最適化が違反する場合における1段階目の最適化に対するペナルティのような位置づけとなります。
2段階目の最適化において、各電力需要における評価値に対し発生確率を掛け合わせています。
今回の確率計画では不確実な需要というリスクを発生確率に対するコストの期待値として加味し、建設から運転に至るトータルコストが経済的となるような発電パターンを求めようとします。
ここで、1段階目と2段階目の問題を1つの最適化問題として整理すると以下の構成となります。
そうすると本問題は整数変数と実数を含む混合整数計画問題（MIP:Mixed Integer Programming Problem）となります。
さらに今回は評価関数ならびに制約がすべて凸な線形形式であるため、混合整数線形計画問題（MILP:Mixes Interger Linear Programming Problem）として解くことができるようになります。
MATLABによるモデリング
確率計画問題の定式化ができたので、これを解くためにMATLABを使ってコーディングしていきたいと思います。
今回、この問題を解くにあたってはOptimization Toolboxを利用します。
また最適化のコーディングは問題ベースのスタイルによって行っていきます。
以前にも問題ベースでMIPのプログラミングをした例を紹介していますので、興味ある方はご覧ください↓
以下がMATLABのコード例です。
% 新設発電所の容量（700MW or 1000MW）
x = optimvar('x',2,'Type','integer','LowerBound',0,'UpperBound',1);
% 既設の石油火力発電所の出力(MW)
yoil = optimvar('yoil',4,'Type','continuous','LowerBound',0,'UpperBound',400);
% 既設のLNG火力発電所の出力(MW)
ylng = optimvar('ylng',4,'Type','continuous','LowerBound',0,'UpperBound',500);
% 不確実な電力需要値(MW)とその発生確立
demand = [700 1000 1200 1600];
p = [0.1 0.2 0.4 0.3];
% 投資は700MWか1000MWのどちらかしか選択できない
eqcons(1) = sum(x) == 1;
% 不確実な需要に対する同時同量の制約
% 新設火力はベースロード一定運転を想定
for i = 1:4
ineqcons(i) = x(1)*700 + x(2)*1000 + yoil(i) + ylng(i) >= demand(i);
end
% コスト関数 (=総費用)
c = [100 400]; % 建設費（固定費）
costFunc = c*x + sum(p*(1*yoil + 0.6*700*x(1) + 0.4*1000*x(2) ...
+ 1.2*ylng));
% ソルバー設定
prob = optimproblem('ObjectiveSense','minimize');
prob.Objective = costFunc;
prob.Constraints.eqcons = eqcons;
prob.Constraints.ineqcons = ineqcons;
options = optimoptions('intlinprog','Display','iter');
% 解法
[solution,fval,exitflag,output] = solve(prob,[],'options',options);
solution.x
solution.yoil
solution.ylng
fval
MILPの解法にはOptimization Toolboxで提供されているintlinprogを用います。
結果
上記コードを実行すると案2の1000[MW]の電源を選択する解を算出しました。
建設費としては案1の方が安いものの、運用にかかる発電コストが案2より高いため、案2を選択しています。
また今回の問題設定では、LNGの価格が油より20%高くしているため、LNGによる発電を抑えて油火力を利用する解を算出しています。
なお、このパターンにおける最終的なコストは1072でした。
ちなみに、同じような最適化問題を扱えるアプリケーションとしてCasADi＆Bonminを利用した場合も試してみました。実行はPython3.8を利用しています。
import casadi
opti = casadi.Opti()
# 変数を定義
x = opti.variable(2)
yoil = opti.variable(4)
ylng = opti.variable(4)
demand = opti.parameter(4)
p = opti.parameter(4)
c = opti.parameter(2)
# 固定値を定義
opti.set_value(demand, [700, 1000, 1200, 1600]) # 電力需要
opti.set_value(p, [0.1, 0.2, 0.4, 0.3]) # 発生確率
opti.set_value(c, [100, 400]) # 建設費
# 目的関数を定義
OBJ = c[0]*x[0] + c[1]*x[1]
for i in range(4):
OBJ += p[i]*(yoil[i]+0.6*700*x[0]+0.4*1000*x[1]+1.2*ylng[i])
opti.minimize(OBJ)
# 制約を定義
opti.subject_to (x[0]+x[1] == 1) # 案1か案2のどちらかしか選択できない
# 同時同量の制約
for i in range(4):
opti.subject_to (x[0]*700 + x[1]*1000 + yoil[i] + ylng[i] >= demand[i])
opti.subject_to( opti.bounded(0, x, 1) ) # 整数変数
opti.subject_to( opti.bounded(0, yoil, 400) ) # 油火力は0 <= yoil <= 400[MW]
opti.subject_to( opti.bounded(0, ylng, 500) ) # LNG火力は0 <= ylng <= 500[MW]
# 最適化ソルバーの設定
p_opts = {'discrete': [True, True, False, False, False, False, False, False, False, False]}
s_opts = {'time_limit': 100}
opti.solver('bonmin', p_opts, s_opts) # 最適化ソルバを設定
sol = opti.solve() # 最適化計算を実行
print(f'評価関数：{sol.value(OBJ)}')
print(f'x: {sol.value(x)}')
print(f'yoil: {sol.value(yoil)}')
print(f'ylng: {sol.value(ylng)}')
for i in range(4):
pow = 700*sol.value(x[0]) + 1000*sol.value(x[1]) + sol.value(yoil[i]) + sol.value(ylng[i])
print(f'Demand: {pow}')
以下が結果になりますが、ほぼ同じ解を算出しています。
（数値的な厳密性がないのは、浮動小数点の影響でしょうかね。。。）
これまでのケースは将来の電力需要が大きく増加する確率が高いという前提で解を算出しました。
今度は別ケースとして、需要がそこまで増加しない、または減少する方向でもどうなるかを検討してみたいと思います。
例として需要の発生確率を{$p^1$, $p^2$, $p^3$, $p^4$} = {30%, 40%, 20%, 10%}とした際の算出解は以下の通りです。
今度は案1を採択しました。需要がそこまで拡大しない場合には建設費の安い案1の方がコストメリットがあるという判断になります。なお、このパターンの時の最適なコストは844でした。
問題が簡単なので、Excelで検算してみると、、、
＜案1採択ケース＞
＜案2採択ケース＞
費用の期待値の合計が、案1では844、案2では904となるのでソルバーの解は確からしいということが分かります。
最後に
という訳で今回は確率計画法を簡単な例題を通じて体験してみました。
今回はリコース関数を用いた2段階確率計画法を試してみましたが、他にも制約条件が満たされる確率を考慮した機会制約問題（Chance Constrainded Problem）のアプローチ等も存在します。
ところで、昨今の世界情勢や世界的な気象現象において、エネルギー情勢の不確実性が増しています。
政府のまとめる資料等を見ても需要の変動や発電設備の稼働状況、燃料在庫などあらゆる面にリスクがあることが言及されています。
実際、今回の例題のような将来の需要見通しに対し、必要な電源投資や供給力確保を促すために容量市場というものが開設されており、将来の安定供給に備えた制度を整えてエネルギー情勢のリスクに備えようとしています。
参考情報