2自由度制御を使ってみよう ～フィードフォワードは伊達じゃない～

2自由度制御とは？

2自由度制御って知っていますか？

制御と言えばPID制御を思いつく人が多いと思います（...そうですよね？笑）
例えば、以下のようなブロック線図表現です。

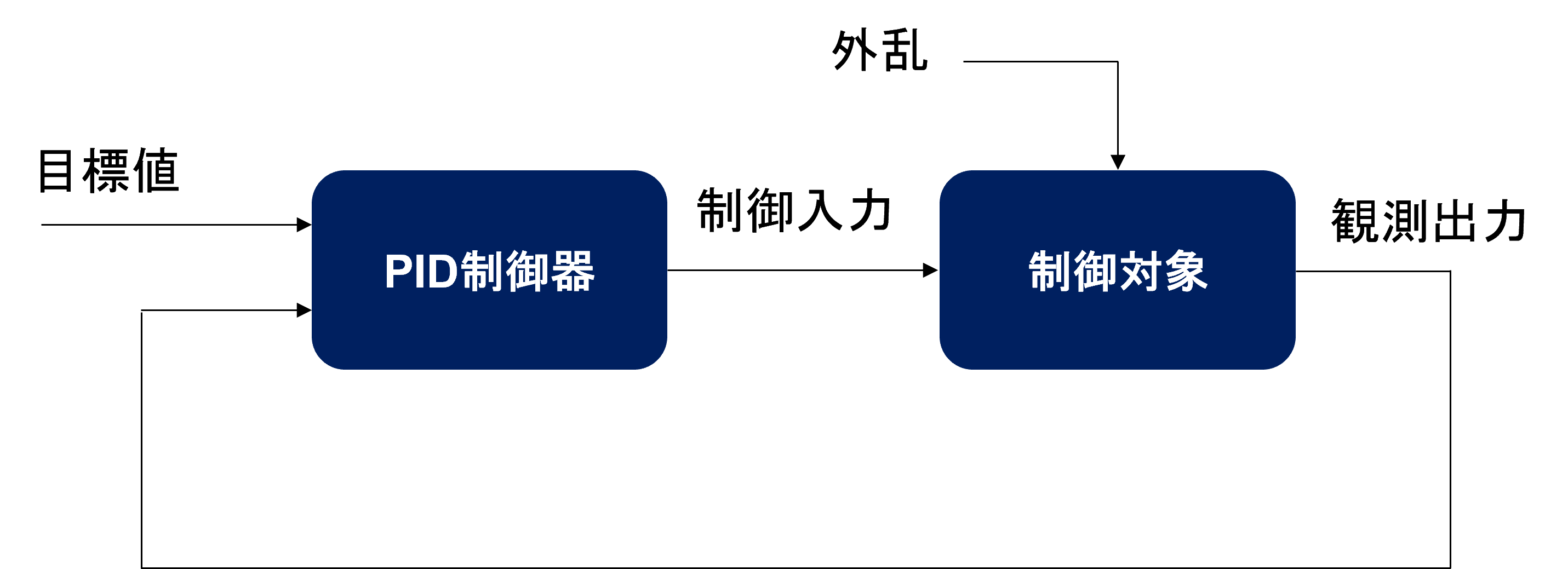
PIDのような制御系は一般に1自由度制御系に分類されます。
なぜ1自由度か。それは、制御器が一つの制御目標にしか対応できないためです。
どういうことかというと、とある制御対象に対し、その出力を所定の目標値に追従させようと考えます。
この時、制御対象には制御入力以外に未知なる外乱が入ってくることを想定します。

そうすると、PID制御では外乱を速やかに抑え込みつつ、出力の追従制御を達成するという2つのタスクをこなすことが必要になります。
人間で言えば、同時に2つの異なるタスクが舞い込んで、同時に処理することに対応します。
想像するとできなくはないが、素直に一つのタスクに打ち込むより、2つのタスクを同時に行う場合の方が効率が落ちることが想像できると思います。

画像：いらすとや

制御も同じです。
PID制御はフィードバック（FB）されてきた観測情報を見て目標値との偏差に基づく制御を行いますが、目標値と出力、外乱という3つの情報をいっぺんに見て、偏差を抑えることと、外乱を抑えることのどちらにも対処しなければなりません。
さらにFB制御では、何かが起こってからしか行動ができないため、どうしても制御のレスポンスが遅くなってしまいます。

よって、PID以外にもう一つ制御器があれば、それぞれ個別にタスクを割りふって制御がうまくできるのではと考えるわけです。

これが2自由度制御の根幹になります。
2自由度制御には様々な構成がありますが、最もメジャーな構成は、フィードフォワード（FF）制御とFB制御を組み合わせたものだと思います。

例えば、上のブロック線図では目標値に対するFF制御を行っています。
こうすることで、目標値信号への追従はFFで行い、外乱の抑制はFB制御で補償してやることが出来ます。

ここで、どうやってFFを設計したら良いのかという疑問が湧くと思います。
FF設計は、対象によってまちまちであり、難しさがあるため、一般化されていません。

ちなみに、、、フィードフォワードのことを書いた日本語の制御工学の教科書は少ないですが、著者が知っている限りだと以下があります。

・森北出版 11ステップ　制御設計―PIDとFFでつくる素性のよい制御系―

・朝倉出版 プロセス制御工学

・日刊工業新聞社 よくわかる機械の制振設計-防振メカニズムとフィードフォワード制御による対策法

話を戻しますが、FFの設計で一般的に多いのは扱う制御対象の逆モデルを使うアプローチです。

ここで、下図のように制御対象を表したとします。（簡単のために出力＝状態としています）
制御対象は出力$y$、状態$x$、そして入力$u$で特性づけられます。
このとき、もし制御対象の特性を表す関数特性$f$（非線形でも線形でも可）の逆関数を定義できるならば、出力$y$から入力$u$を計算することが出来ます。
出力$y$を所定の目標値として考えれば、その目標値を達成するために必要な入力$u$が逆説的に求まるということです。
これが制御対象の逆モデルを使ったフィードフォワード制御器の設計方法の一つです。

シミュレーションによる数値実験

それでは、例題を通じて2自由度制御の設計とパフォーマンス評価をSimulinkを使ってやっていきたいと思います。

今回取り扱う例題は、脱硝制御です。
脱硝制御は、ボイラーなどの燃焼機関で発生する燃焼ガス中に含まれる窒素酸化物（NOx）をアンモニア（NH3）による還元反応によって無害なH2O、H2に分解し処理するための制御です。
NOxは環境や人体に有害な酸化物であり、火力発電や化学プラント、ディーゼルエンジンなどの排ガス中に含まれます。

上図は脱硝プロセスの模式図です。
機関で仕事を終えたガスは煙道を通じて大気中に放出されますが、この間に反応用の触媒を配置し、NH3をスプレーすることによって還元反応を生じさせます。
脱硝制御では、煙道の出口側にNOxの濃度を計測するためのセンサーを設け、検出した濃度に応じ、NH3の注入量を制御します。

この脱硝プロセス、実は長いむだ時間を持つ非常に制御がしづらい系として知られています。
最もむだ時間が大きいのはNOxセンサーであり、計測に数分オーダーの時間を要するため、強いFB制御を行うと閉ループが不安定となり制御が発散してしまいます。
またNOxは自治体ごとに環境規制値が設けられており、火力プラントなどでは常時排出量が監視され、規制値を超えるとアラートが飛び、プラントの操業に影響を及ぼします。

東京都環境局 窒素酸化物に係る規制基準

以上の事情から、FB制御のみでは不十分な制御であり、FFやモデル予測制御などの予測を活用した制御が行われています。

【参考文献】
計測と制御 第39巻 第5号 2000年5月号 一般化予測制御の発電プラントへの応用

では、上記文献を参考に線形近似された脱硝プロセスを題材にシミュレーションで2自由度制御の効果を確認してみます。

上図は脱硝プロセスの線形モデルであり、図中の$G$は入力であるNH3の輸送や触媒でのNOxとの反応遅れに起因する特性を表しており、$Gsen$はNOxセンサーの計測遅れを表しています。
各遅れはプロセス系として、以下の一次遅れ＋むだ時間系です。

G = \frac{-1}{10s+1}e^{-10s}

Gsen = \frac{1}{30s+1}e^{-120s}

見ての通りセンサーのむだ時間が120秒とかなり大きいです。

この系を対象に以下の構成でFBならびにFFによる2自由度制御器を設計していきます。

ここで、各制御器の目的は以下です。

FF制御器：外乱であるNOx発生量の影響を抑える
FB制御器：NOxの濃度目標値に対する出力の追従を行う

実際に2自由度制御系が各々の設計目標に対し、対応可能なことを閉ループの伝達関数から示します。

まず目標値rから出力yまでの閉ループ伝達関数は次式となります。

T_{ry} = \frac{GGsenFB}{1+GGsenFB}

一方で外乱dから出力yまでの閉ループ伝達関数は次式となります。

T_{dy} = \frac{Gsen(1+GFF)}{1+GGsenFB}

各伝達関数において分母にはFB制御器の特性が共通して入っていますが、分子では、各々FB、FFが独立しています。
よって各制御目標について、FB及びFF制御器を使って独立に指定できることが分かります。

それでは、まずFFを設計しましょう。
FFは、$T_{dy}$の分子がゼロとなれば、外乱$d$が出力$y$に与える影響を0にすることが出来ますので、制御対象の逆モデルを計算して次式のように求めることが出来ます。

1+GFF = 0

FF =  -\frac{G_f}{G}

ここで新たな変数$G_{f}$を追加しました。これはFFがプロパー（伝達関数の分母の次数が分子の次数より等しいか大きい）になるように挿入したフィルターです。
フィルターは安定で定常ゲイン(t→∞)が1であれば何でも良い、というと誤解を生みそうですが、外乱抑制についての応答性を調整することができます。
なお、FFを設計する際にプラントのむだ時間の項がありますが、取り扱いが煩わしいので今回は無視して扱うことにします。
※今回はFFを構成するにあたり外乱を計測できるという前提で組んでいます。NOxの発生量は内燃機関側の物理量と相関があるので、事前に推定することが出来る場合があります。

一方、FB制御器はPIDによってオーソドックスに設計します。

シミュレーションでは、NOx濃度の目標値に出力$y$を追従させるとともに、途中でNOx発生量の変動がステップ状に発生するというシナリオを考えます。

実際に利用したSimulinkのモデルは以下となります。

モデル全体図

コントローラーサブシステム図

なお、FFの実装にはLTI Systemブロックを使用しています。

また設計のためのMATLABコードは以下です。

～コード例～

% 2 degree of freedom control 
% Plant dynamics
s = tf('s');
G = -exp(-10*s)/(10*s+1);

% Sensor dynamics
Gsen = exp(-120*s)/(30*s+1);

% Controller
ts = 1; % サンプリング時間
Kp = 0.4466;   % Pゲイン
Ki = 0.0047;   % Iゲイン
Kd = -21.3073; % Dゲイン
N = 0.0053;

% FF制御器
G_nodelay = -1/(10*s+1);
Gf = 1/(s+1);
KFF = c2d(-Gf/G_nodelay,ts);

なお、FF＆FB制御器はサンプリング時間（1s）で離散化して組み込んでいます。
またPIDのパラメーターの決定にはSimulink Control Design™で提供されているPID調整器を利用しました。

ではシミュレーション結果を見てみましょう。

上図は最上段が出力$y$、中段が外乱$d$、下段が入力$u$に関するトレンド結果を示しています。

まず出力については、黒の破線が目標値$r$、ピンクの実線がFFなし、青の実線がFFありの応答を示しています。
当然ではありますが、目標値への追従性に関しては、FFの有無による差異はありません。
しかし、外乱発生後の応答については差異が生じていることが分かります。
見ての通り、圧倒的にFFがある方が外乱を速やかに抑制しています。

続いて、入力$u$の結果を見てみると、ピンクの実線で示すFFなしに対し、青の実線で示すFFありの応答では、外乱発生と同時に入力が大きく動き、適切に外乱を補償していることが確認できます。

以上からFFによる2自由度制御の効果を簡単に確認できました。

これが実際のNOxプロセスで運転したと考えた場合、NOx排出量を大きく抑えることに貢献します。
適切な制御系を設計することは社会や環境に大きく貢献するのです！

まとめ

今回は2自由度制御系についての考察を行い、シミュレーションによる評価によってそのアドバンテージを確認することができました。

例題では、SISO系に対しての設計でしたが、MIMO系を考慮した場合にはもう少しシステマチックにやりたいという願望が出てきます。
MIMOに対する2自由度制御系の構築について、いずれやってみようかなと思います。