MATLABによるロバスト制御の設計

はじめに

今回はロバスト制御について書いてみようと思います。
ところで、皆さんはロバスト制御という言葉を知っているでしょうか？

PID制御に代表される一般的な制御手法は確定的なノミナルモデルをベースに制御性や安定性を保証するのに対し、ロバスト制御はモデルの不確定な変動をも考慮し、安定性や制御性能を追求するためのロバスト（堅牢）な制御を提供する手法です。

ロバスト制御の歴史は古く、1980年代には主な理論体系が確立し、90年代初頭では盛んに実用研究がなされていました。

その一つとして、現在のJAXAの前身であるNAL（航空宇宙技術研究所）及びNASDA（宇宙開発事業団）が進めていた日本版スペースシャトル計画HOPEの自動着陸技術獲得のための実験機ALFLEX（Automatic Landing FLight EXperiment）という機体がありました。

この機体は、推力なしで自動着陸を行うように飛行制御システムが設計されていました。
実験機ということで、スケール機であることに加えて、再突入を意識した形状のために不安定な特性を持っていること、飛行中に突風など様々な不確定外乱が想定されることなど、種々の条件から自動着陸のための飛行制御系にはロバスト性が求められました。
さらに無推力のためにやり直しの効かない一発勝負の着陸となるため、当時の最新制御ということでロバスト制御の一つであるH∞制御が適用されました。
なお、国内で初めて飛行制御にH∞制御を実装したのがALFLEXだと言われています。

実験自体は1996年の夏にオーストラリアのウーメラで行われ、計13回の飛行実験において全て無事に着陸できたそうです。

ロバスト制御の基本的な考え方

ここでは、ロバスト制御の設計に際し、必要となる基本知識を簡単にまとめたいと思います。
なお、まとめるにあたり下記の本を参考にさせて頂きました。$^{[1]}$

ロバスト制御の考え方や応用例がMATLABのコードと共に非常に分かり易く解説されておりますので、詳細を知りたい方はぜひ一冊入手することをお勧めします。

まず、ロバスト制御のみならずフィードバック制御を考える際によく出てくる感度関数、相補感度関数について考えます。
下図に示すようにとあるフィードバック制御系を考えた際に、目標値から出力までの伝達特性を閉ループ伝達関数として計算できますが、これは相補感度関数Tとして定義されます。
一方、目標値から偏差までの伝達特性を計算した結果を感度関数Sとして定義されます。

そして、感度関数Sと相補感度関数Tの間には常に成り立つ恒等式$S+T=1$があります。
この恒等式は、周波数特性上すべての帯域で満たされる強い性質となっています。

同じように外乱から出力、ノイズから出力の伝達特性を計算してみるとそれぞれ感度関数、相補感度関数が入り込んでいることが分かります。

フィードバック制御系を検討するにあたり、さまざまな制御性能を評価すると思います。
一つは目標値に対する追従性がありますし、他方では外乱やノイズに対する耐性等さまざまです。

各制御に求められる要件を感度関数と相補感度関数という2つの周波数特性上の指標から評価すると下表のような関係となります。

分かるのは各要件ごとに求める特性が異なるということです。
そして、上述したように感度関数と相補感度関数の間には恒等式という強い制約があるため、全ての要件を全周波数帯域で満足させることはできないことが分かります。

そのため、周波数特性上で相対する要求に妥協点を見つけて、求める制御性能が満たされるように上手く周波数応答を整形してあげることが必要となります。
これは古典制御の一つでもあるループ整形法の考え方に由来します。

続いて、不確かさの表現方法です。
ロバスト制御では制御対象であるプラントPについてその変動も考慮した設計を行います。
その変動を不確かさとしてどのように見積もるかによっても得られる結果が変わってくるものとなります。

上図は不確かさを乗法的不確かさとして表現した際におけるその取り扱いの違いを示したものとなります。
一方は摂動を一つの項としてまとめてしまう非構造的な摂動表現を元にした場合、もう一方は摂動の構造情報を維持した構造的摂動表現の場合を示しています。
ちなみに一般的に非構造的摂動表現を扱うロバスト制御問題はＨ∞制御、構造的摂動表現を扱う問題はμ設計法として解かれます。各制御手法の概要は後程紹介します。

続いて、ロバスト制御を扱う上で重要なプラント表現である一般化プラントを紹介します。
一般化プラントとは、下図に示すようにあるプラント$G$について、その入力に制御入力$u$以外に外生入力$w$を考えます。$w$には目標値や外乱などが信号として当てはまります。
そして、$G$の出力として観測される出力$y$以外に被制御量$z$というものを評価します。

フィードバック制御器である$K$は、結局のところ、いかなる外生入力が入ってきても被制御量$z$への影響を小さくすることが主な役割として期待されます。

この影響度合いをH∞ノルムを使って評価して、それを最小化するような制御器Kを設計する問題をH∞（エイチインフィニティまたはエイチ無限大）制御と呼びます。
H∞ノルムですが、SISOでは定義が簡単で、ボード線図のピークゲインがそれにあたります。

続いて、ロバスト制御の重要な定理であるスモールゲイン定理も紹介します。
スモールゲイン定理とは、とあるシステムMに対し、変動Δが存在する場合、下図のようにMとΔの積に関するノルムが1以下となれば、閉ループは安定であることを証明します。

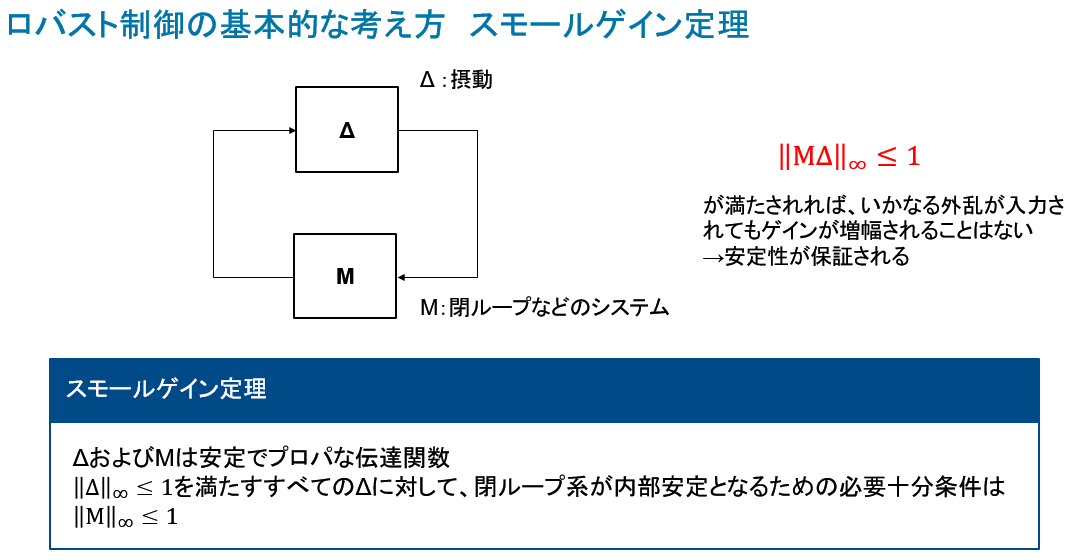
このスモールゲイン定理があることによってロバスト制御の安定性が保証されます。

今日におけるロバスト制御としては、H∞ノルムの最小化を狙うH∞制御、構造化特異値μの最小化を狙うμ設計法の大きく２つがあります。

本記事では、H∞制御によるロバスト制御系の設計をMATLABを使ってやってみたいと思います。

H∞制御の設計

それでは、H∞制御によるロバスト制御系設計を試していきたいと思います。$^{[1],[2],[3]}$
設計に際しては、MATLABの製品ファミリーであるRobust Control Toolboxを使用します。

制御対象

題材として航空機のピッチ角制御を扱いたいと思います。

航空機には縦運動を制御するための制御舵面として、一般に水平尾翼にあるエレベーター（昇降舵）というものがあります。

航空機はこのエレベーターを使用して、機体に働く空力モーメントを変化させることで縦方向を制御します。

今回機体のノミナルモデルとして、以下の縦運動の線形状態空間モデルを使用します。
（行列内の各シンボル名は適当です）

本モデルはエレベーター舵角を入力、機体のピッチ角を出力とするSISO系です。

またエレベーター舵角を発生させるアクチュエーターダイナミクスとして上記のように一次遅れを考慮します。
ここで、下付き添え字CはCommandを意味しています。

不確かさの考慮

縦運動の線形システムのノミナルなパラメーター値については、ジャンボジェットの愛称で知られるBoeing747の巡行形態時（高度40000ft(12192m)、Mach 0.8）における値を使用します。$^{[4]}$

ノミナル値

Xu = -0.0028;
Xa = 9.1771;
Xq = -18.9201;
Xth = -9.7784;
Zu = -0.0003;
Za = -0.3191;
Zq = 0.9813;
Zth = -0.0034;
Mu = 0.0007;
Ma = -0.7841;
Mq = -0.4271;
Mth = 0.0003;
Xde = 0.4389;
Zde = -0.0233;
Mde = -1.1579;
Tde = 1;

上記のノミナル値に対し、それぞれ不確かな変動を考慮します。
Robust Control Toolboxではパラメーターの変動を考慮するための機能としてurealという関数が用意されています。

この関数では、ヘルプの記述にある通り、±、範囲、％、の3つから各々変動の表現を行うことが出来ます。
次に示すコード例ではそれぞれの表現方法を示します。

urealによる変動の考慮

% 公称値に対する割合を用いた表現
Xu = ureal('Xu',Xu,'percent',5);
Xa = ureal('Xa',Xa,'percent',5);
Xq = ureal('Xq',Xq,'percent',5);
Zu = ureal('Zu',Zu,'percent',5);
Za = ureal('Za',Za,'percent',5);
Zq = ureal('Zq',Zq,'percent',5);
Zth = ureal('Zth',Zth,'percent',5);
Mu = ureal('Mu',Mu,'percent',5);
Ma = ureal('Ma',Ma,'percent',5);
Mq = ureal('Mq',Mq,'percent',5);
Mth = ureal('Mth',Mth,'percent',5);

% 公称値を含む区間による表現
Xde = ureal('Xde',Xde,'Range',[0.3 0.5]);
Zde = ureal('Zde',Zde,'Range',[-0.03 -0.01]);

% 公称値を基準とした増減による表現
Mde = ureal('Mde',Mde,'PlusMinus',[-0.1 0.1]);    
Tde = ureal('Tde',Tde,'PlusMinus',[-0.2 0.2]); 

以上の値を基にして制御対象である状態空間モデルを構成します。

モデルの定義

% 縦の運動モデル
A = [Xu Xa Xq Xth;
     Zu Za Zq Zth;
     Mu Ma Mq Mth;
     0 0 1 0];
B = [Xde;Zde;Mde;0];
C = [0 0 0 1];
D = 0;
P = ss(A,B,C,D);
P.InputName = 'de';
P.OutputName = 'theta';
Pnom = P.NominalValue;   % ノミナルモデルの取得

% アクチュエーターモデル
Pact = tf(1,[Tde 1]);
Pact.InputName = 'de_c';
Pact.OutputName = 'de';

% 統合モデル
Pall = P*Pact;
Pall_nom = Pall.NominalValue; % ノミナルモデルの取得

ここで定義されるモデルは不確かなパラメーター変動を含んだモデルとなり、ussという専用のモデルオブジェクトとなります。
ノミナル値に対するモデルを取得したい場合には、ussオブジェクトのフィールドプロパティにあるNominalValueにドット(.)付でアクセスすることが可能です。

それでは定義したモデルの周波数応答を確認してみましょう。

周波数応答の確認

sample = 50;    % 標本数
clf,bode(usample(Pall,sample),'b--',Pall_nom,'r-'),legend('P_uncertain','P_nominal')

usample関数を使うと、ussのモデルから乱数によって指定したサンプル数だけ不確かな変動モデルを抽出することが出来ます。

上図の青破線が不確かさを考慮した50サンプル分のモデル、赤実線がノミナルモデルの周波数応答を示しています。
図を見ると変動が全帯域に亘り乗っかっていることが確認できます。

よくモデルの不確かさの影響が高周波帯域に強く現れるケースを見ますが、このモデルではそういった傾向はないようです。

周波数重み関数の設計

前節にて不確かなモデルの定義が出来たので、このモデルに対しH∞制御のための重みの設計を行っていきます。
モデルの不確かさに伴う変動については、下図のような乗法的不確かさとして扱うこととします。

乗法的不確かさの見積もり

w = logspace(-4,1,100);
Pall_g = ufrd(Pall,w);
Delta = (Pall_g-Pall_g.NominalValue)/Pall_g.NominalValue;
clf,bodemag(Delta,'b--',w),legend('Delta')

上図はサンプル点数分の乗法的不確かさをプロットしています。
これを見ると、0.07~0.1[rad/s]あたりにあるピークゲインのところがクリティカルに影響しそうなことが分かります。

それでは、乗法的不確かさを抑える込むことを目的として周波数重み関数を設計していきます。
通常、重みの設計は試行錯誤しながらやっていくことが多いですが、Toolboxでは重みを自動で計算、サポートしてくれる関数ucoverがありますのでこれを使っていきたいと思います。

ucover関数では、ussオブジェクトとノミナルモデル、そしてフィットさせる次数を与えるだけで不確かさを包含した重み関数（フィルター）を設計することが出来ます。

乗法的不確かさに対する周波数重み関数の設計

fit_odr = 2;
[~,info] = ucover(usample(Pall_g,sample),Pall_g.NominalValue,fit_odr);
Wm = info.W1;
clf,bodemag(Delta,'b--',Wm,'r-',w),legend('Delta','Wm')

上図は先ほどの乗法的不確かさのプロットに、ucoverによって計算された周波数重み関数$W_m$を重ね書きした結果となります。
不確かな変動をすべて覆うように重み関数が設計されていることが確認できます。
なお、次数は2次として重み関数を設計しています。

今回はこの重み関数をそのまま相補感度関数の重みとして扱っていきたいと思います。

相補感度関数の周波数重み関数

Wt = Wm;

また上記以外に、感度関数、アクチュエーターの重みを次のように設計します。

各重み関数の設計

% 感度関数の重み
Ws = tf(1,[1 0.001]);
% アクチュエーターの重み
Wde = tf(1); % ゲイン＝1
% 周波数応答の確認
clf,bodemag(Ws,Wt,Wde,w),legend('Ws','Wt','Wde');

ここで、各重みは試行錯誤を交えつつ、次の方針で設計を行いました。

・感度関数　　　　：低周波帯域における外乱抑制および制御偏差の抑制
・アクチュエーター：アクチュエーターの過剰動作の抑制

なお、重みの設計についてはucover以外にもmakeweight関数を使うこともできます。

一般化プラントの定義

重みの設計ができたので、続いて一般化プラントを定義します。
今回検討する一般化プラントは下図の通りとします。

一般化プラント$G$への入力として、上から入力端外乱$d$、ピッチ角の目標値$ref$、エレベーター舵角の指令値$\delta_{ec}$を考えます。
また出力としては、被制御量$z_1$~$z_3$と制御偏差$e$を考えます。

コードによる一般化プラントの定義では、各伝達特性についてその入出力のシンボルを定義し、connect関数やsumblk関数等を使うことで構成可能です。

一般化プラントの定義

P.InputName = 'u'; P.OutputName = 'theta';
Ws.InputName = 'e'; Ws.OutputName = 'z1';
Wt.InputName = 'theta'; Wt.OutputName = 'z2';
Wde.InputName = 'de'; Wde.OutputName = 'z3';
Sum1 = sumblk('e = ref - theta'); % 加減算要素の作成
Sum2 = sumblk('u = de + d');      % 加減算要素の作成
G = connect(P,Pact,Ws,Wt,Wde,Sum1,Sum2,{'d','ref','de_c'},{'z1','z2','z3','e'});

H∞制御器の設計

一般化プラントが定義できたら、続いてはH∞制御器を設計します。
Robust Control Toolboxでは、H∞制御の設計を行うための専用関数hinfsynを提供しています。

hinfsyn関数では一般化プラントと一般化プラントにおける制御入力および観測出力に関する数を指定することでH∞ノルムを最小化する制御器$K$を計算することが出来ます。
またhinfsynOptions関数にて各最適化ソルバーのオプションを詳細に設定することが可能です。

hinfsyn

opts = hinfsynOptions('Method','RIC','display','on');   
[K,CL,gamma] = hinfsyn(G,1,1,opts); % 第2引数：nmeas = 観測出力数 第3引数：ncont=制御入力数

H∞制御器の設計にはγイタレーションという手法を使い収束計算を行います。
スカラーであるγの値が1以下となると所定の性能を満たす制御器が見つかったことを示します。

今回の場合はγの最小値が2.22ということで期待される1以下とはなりませんでした。
しかし、1に近い値であるため、ある程度の性能を満たしている可能性があります。
そのため、設計したコントローラーに対し、感度関数や相補感度関数を解析して結果の評価を行ってみたいと思います。

まず得られたH∞制御器の周波数応答を確認してみます。

H∞制御器の周波数応答

clf,bodemag(Pnom,K),legend('Pnom','K')

なお図中、赤線がH∞制御器、青線が制御対象のノミナル値です。

続いて、感度関数、相補感度関数を計算して表示してみます。

性能解析

T = feedback(P*Pact*K,1);    % 相補感度関数
S = feedback(1,P*Pact*K);    % 感度関数

figure,clf
subplot(221),bodemag(T,'-',1/Wt,'r--'),grid on,title('complementary sensitivity function')
subplot(222),bodemag(S,'-',1/Ws,'r--'),grid on,title('sensitivity function')
subplot(223),bodemag(Pact*K*S,'-',1/Wde,'r--'),grid on,title('Actuator output')
subplot(224),bodemag(P*S,'-'),grid on,title('Disturbance output')

図中、上段が左から相補感度関数、感度関数、下段が左から目標値$ref$からアクチュエータ出力${\delta}_e$までの伝達特性、外乱$d$から出力$\theta$までの伝達特性をそれぞれ表示しています。
また赤色破線はそれぞれ重みの逆数を表示しています。

結果を見ると、図中右上の感度関数にて低周波帯域におけるゲインが仕様より上回っていることが分かります。
本来、感度関数はこの帯域において-60[dB]以下にしたかったため、これが性能を満足できていない箇所となることが分かります。
ただし、それでも十分にゲインは小さくなっているので外乱や制御偏差の抑制という観点においては十分かもしれません。

相補感度関数については、制御として想定する帯域幅において0[dB]（ゲイン＝1）となっており期待する性能を満足しています。

アクチュエーター出力については、1[rad/s]以下の低周波帯域でゲインの抑え込みに成功しているものの、1～100[rad/s]の周波数帯で仕様を超過しています。
これもγ>1となる要因のようです。

外乱の出力への影響については、メインとなる低周波帯域で十分に低減できていることが分かります。

最後に閉ループ特性について時間領域でも確認しておきます。

ステップ応答の確認

figure,clf
step(T),grid on

結果を見るとすべてのケースで応答は発散することなくステップ値1の近傍に到達できています。
よってロバスト性を有しつつ、ある程度のパフォーマンスを備えた制御器であることが分かります。

Simulinkへの実装

設計した制御器をSimulinkに実装します。

得られたH∞制御器は状態量を持つ動的なコントローラーです。
よって、Simulinkで実装する場合にはState Spaceブロックを利用できます。

閉ループモデルとして下図のモデルを用意します。

シミュレーションでは、ピッチ角の目標値として5[deg]のステップ応答を入れて、きちんと安定に追従できるかを確認します。
また途中に入力端からステップ外乱を印可することで、外乱に対する性能も確認します。

上図がSimulinkによるシミュレーション結果であり、上からピッチ角、エレベーター舵角、外乱のトレンドを示しています。

ピッチ角はステップ状の目標値に対し、多少オーバーシュートしながらも良好に追従していることが分かります。
また100秒後にステップ状の外乱が発生しますが、これも速やかに影響を抑制できていることが分かります。

エレベーター舵角ですが、制御器から生成される舵角の指令値は最初に大きな値となるものの、その後は過大な値が生成されることはなく、現実的なアクチュエーターの動作範囲内で収まっていることが分かります。

この時の飛行の様子をアニメーションにしたものが以下になります。（3倍速）

ちなみに、比較としてアクチュエーター出力の抑制ならびに外乱抑制を考慮せずにH∞制御器を設計した場合における同シナリオの結果を下図に示します。（縦軸のスケールが先ほどの図とは異なります）

結果を見ると、外乱に対する出力の減衰性が悪いことが分かります。
またエレベーター舵角も振動的な値となっており、その結果ピッチ角にも影響が大きく現れています。

続いて、モンテカルロシミュレーションによりパラメーターが変動したケースに対する応答も確認しておきたいと思います。

制御対象モデルとして使用しているブロックには、Uncertain State Spaceブロックを使っています。

このブロックの不確かさの値フィールドにusample関数を使って実行毎に異なるパラメーターセットを与えることでモンテカルロシミュレーションを行うことが出来ます。

Simulinkによるモンテカルロシミュレーション

uvars = ufind(mdl);  % mdl：モデル名を指定します
ublk1 = strcat(mdl,"/Longitudinal Plant");
ublk2 = strcat(mdl,"/Actuator");
set_param(ublk1,"UValue","usample(uvars)");
set_param(ublk2,"UValue","usample(uvars)");
out = [];
MCS = 50;            % シミュレーション回数
for i = 1:MCS
    out = [out; sim(mdl)];
end

figure,clf
yyaxis left
xlabel('time[s]')
ylabel('pitch angle [rad]')
yyaxis right
ylabel('elevator angle [rad]')
hold on
for i = 1:MCS
    y = out(i).logsout.get('y').Values.Data;
    de = out(i).logsout.get('de').Values.Data;
    t = out(i).logsout.get('y').Values.Time;
    yyaxis left
    plot(t,y,'b-'),grid on,hold on
    yyaxis right
    plot(t,de,'r-'),grid on,hold on
end
hold off

50回の標本ケースに対するシミュレーション結果が上図の通りとなりますが、全てのケースで問題は特になさそうです。
よって、想定される変動に対して制御系は期待されるロバスト性を発揮していることが分かります。

最後に実際にフライトコントローラー等のデジタルプロセッサに制御を実装する際には、制御器を離散化することが必要となります。
Control System Toolboxでは、モデルを離散化するためのコマンドやアプリ機能を提供しているので簡単に離散化に取り組むことができます。

制御器の離散化

Kd = c2d(K,0.01,'tustin'); % 制御周期10msでタスティン変換を用いて離散化
bode(K,Kd),legend('continuous','discrete')

タスティン変換で離散化した制御周期10msの制御器は連続時間のものと比較して乖離が少ないことが分かります。
同様にシミュレーション結果も大きな乖離がなかったので掲載は省略します。

最後に

今回はロバスト制御の1つであるH∞制御について、MATLAB及びSimulinkでどのように設計、解析できるのか簡単にやってみました。
不確かな変動に対するロバスト性を発揮できる点はやはり強力な制御手法だと改めて感じます。

ただし、過剰な変動を見積もると制御器が保守的になってしまい、期待する制御性能を発揮できないケースもあります。
また得られる制御器の次数が一般化プラントのものと同じであるため、複雑な対象となるほど次数が大きくなって実装時には制御器の低次元化を検討しなければならないケースがあります。

ただし、近年はこの制御器の構造問題について、構造が固定化された制御器に対するロバスト制御問題を解くアプローチが登場してきています。
そのため、例えば現場ですでに実績あるPID制御器をロバスト制御の観点でチューニングするということも検討できるようになっています。

次回は構造固定化された制御器に対するロバストな制御系設計にトライしてみようと思います。

参考文献

[1] 平田光男、実践ロバスト制御、コロナ社
[2] 赤阪大介、Robust Control Toolbox™による構造が固定された制御系の解析・設計、計測と制御 第59巻 第3号 2020年3月号
[3] https://jp.mathworks.com/help/robust/gs/using-mixsyn-for-h-infinity-loop-shaping.html
[4] 嶋田 有三、佐々 修一 著：飛行力学, 森北出版株式会社