はじめに
イーロンマスク率いるSpaceXでは、火星や月飛行に向けたロケット開発を進めています。
特にStarshipは、現行ロケットの中でも最大級のロケットエンジンを備えており、Falcon 9ロケットのような部分再使用ではなく、完全再使用可能なRLV(Reusable Launch Vehicle)を目指して開発が進められています。
またFalcon 9と同様に自律的な着陸制御技術によって、機体の姿勢を維持し、定められた軌道及び着陸ポイントまで飛行することが可能なシステムとなっているようです。
前回の記事にて、SpaceXのロケットの制御にはモデル予測制御(MPC)が使われているらしいということで、実際に簡単なロケットの非線形運動モデルをベースにシミュレーションを行いました。
今回は前回の内容からもう少し踏み込んだシミュレーションを行ってみたいと思います。
6自由度の非線形運動方程式
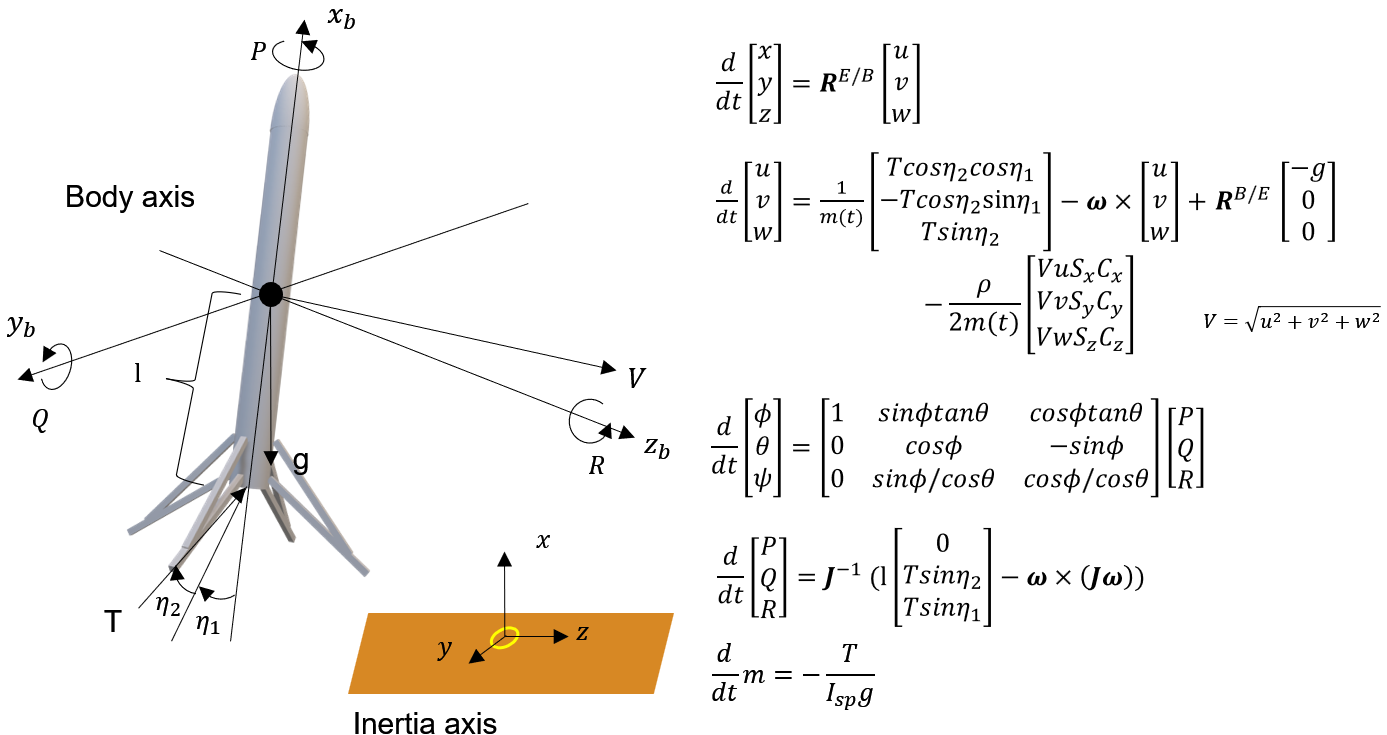
今回検討に用いるロケットの運動モデルは、X,Y,Zの3次元空間内における位置ならびに姿勢を考慮した剛体運動と仮定して、6自由度の非線形運動方程式を構築していきます。
ここでロケットはエンジンで燃料を燃焼させることで推力を得ますが、燃料を消費することで機体の質量がその時々で変化する非線形性の強い対象として知られています。
加えて、惑星の大気中を航行する際には機体に掛かる抵抗といった空気力、風等の様々な不確定外力が生じるため、予測の難しい複雑な制御対象となります。
よって、MPCを設計するためには、まず上記を含んだ運動モデルを式として用意することが大前提になります。
そのため、下図に示すような質量変化ならびに空気力を考慮した6自由度の非線形運動方程式を定義します。
本モデルは実際のロケット制御に用いられるような厳密なモデルではありません。
本記事内だけで有効なモデルですのであしからず。
なお、状態量としては13個あり、そのすべてがセンサー等によって観測可能であるとします。
またロケットの制御方式としては、スラストベクタリング(TVC)を前提とします。
したがって、制御入力としては推力$T$、各軸方向のジンバル角($\eta_1$, $\eta_2$)の計3つを取り扱うこととします。
数式ツールを使った運動方程式コードの自動生成
前章でロケットの運動方程式が立式できたので、これをMATLABの関数コードとして用意します。
MATLABの製品ファミリーであるSymbolic Math Toolboxでは、シンボリックな数式表現を元に、変数同士の四則演算や行列演算、さらに微分・偏微分等を行えるだけでなく、それらの結果から自動的にMATLABやCなどでコード生成が行える機能があるので、これを使って運動方程式からMATLABの関数コードを自動生成したいと思います。
まずシンボリックな変数を定義するためには、symやsymsコマンドを利用します。
また定義した式からヤコビアンやヘシアンを計算する際には、jacobian、hessianコマンドを利用することが可能です。
最終的に生成した各式のオブジェクトからコードを自動生成する際には、matlabFunctionコマンドやccodeコマンドが利用可能です。
上記機能を使ってロケットの運動モデルのコードを生成するスクリプトが下記になります。
% States
syms xe ye ze u v w phi theta psi p q r m
x1 = [xe;ye;ze];
x2 = [u;v;w];
x3 = [phi;theta;psi];
x4 = [p;q;r];
states = [x1;x2;x3;x4;m];
V = sqrt(u^2+v^2+w^2);
% Inputs
syms T ita1 ita2
inputs = [T;ita1;ita2];
% Pareameters
syms s_L s_radius s_Ixx s_Iyy s_Izz s_g s_Sx s_Sy s_Sz s_Cd s_rho s_Isp s_MainThrust
I = diag([s_Ixx,s_Iyy,s_Izz]); % Inertia matrix
% Additional input parameters for NMPC
syms Q Qn R;
% Rotation Matrix
% Body to Inertia
Reb = [cos(psi)*cos(theta) cos(psi)*sin(theta)*sin(phi)-sin(psi)*cos(phi) cos(psi)*sin(theta)*cos(phi)+sin(psi)*sin(phi);
sin(psi)*cos(theta) sin(psi)*sin(theta)*sin(phi)+cos(psi)*cos(phi) sin(psi)*sin(theta)*cos(phi)-cos(psi)*sin(phi);
-sin(theta) cos(theta)*sin(phi) cos(theta)*cos(phi)];
% Inertia to Body
Rbe = [cos(psi)*cos(theta) sin(psi)*cos(theta) -sin(theta);
cos(psi)*sin(theta)*sin(phi)-sin(psi)*cos(phi) sin(psi)*sin(theta)*sin(phi)+cos(psi)*cos(phi) cos(theta)*sin(phi);
cos(psi)*sin(theta)*cos(phi)+sin(psi)*sin(phi) sin(psi)*sin(theta)*cos(phi)-cos(psi)*sin(phi) cos(theta)*cos(phi)];
% Angular velocity matrix
R_ang = [1 sin(phi)*tan(theta) cos(phi)*tan(theta);
0 cos(phi) -sin(phi);
0 sin(phi)/cos(theta) cos(phi)/cos(theta)];
% State Function
f = [Reb*x2;
1/m*([s_MainThrust*T*cos(ita2)*cos(ita1) -s_MainThrust*T*cos(ita2)*sin(ita1) s_MainThrust*T*sin(ita2)]')-cross(x4,x2)+Rbe*[-s_g 0 0]'-s_rho/(2*m)*[V*u*s_Sx*s_Cd V*v*s_Sy*s_Cd V*w*s_Sz*s_Cd]';
R_ang*x4;
inv(I)*(0.5*s_L*[0 s_MainThrust*T*sin(ita2) s_MainThrust*T*sin(ita1) ]'-cross(x4,I*x4));
-s_MainThrust*T/(s_Isp*s_g)];
f = subs(f,[s_L s_radius s_Ixx s_Iyy s_Izz s_g s_Cd s_Sx s_Sy s_Sz s_rho s_Isp s_MainThrust],[L radius Ixx Iyy Izz g Cd Sx Sy Sz rho Isp Main_Thrust]);
f = simplify(f);
% Jacobian
A = jacobian(f,states);
B = jacobian(f,inputs);
% Generate MATLAB Function Code
matlabFunction(f,'File','./source/landerStateFcn','Vars',{states,inputs,Q,Qn,R});
matlabFunction(A,B,'File','./source/landerStateJacobianFcn','Vars',{states,inputs,Q,Qn,R});
なお、機体や環境に関する事前定義されたシンボリックなパラメーター変数(s_Lやs_radius等)には、subsコマンドを利用することで実際の値を代入し、処理することが可能です。
今回は以下のパラメーターを使っていきます。
特に重力加速度や空気密度は、火星の値として考慮しています。
% Initial mass
mass = 500e3;
dry_mass = 0.7*mass;
% Length
L = 47.5;
% Radius
radius = 1.865;
% Inertia
Ixx = 0.5*mass*radius^2;
Iyy = (radius^2/4 + L^2/12)*mass;
Izz = Iyy;
% Representative area
Sx = pi*radius^2;
Sy = L*2*radius;
Sz = Sy;
% Drag coefficient
Cd = 2;
% Specific impulse
Isp = 348;
% Gravity of Mars
g = 3.721;
% Air density of Mars
rho = 0.0118;
% Main Thrust
Main_Thrust = 5*mass*g;
% RCS Thrust
RCS_Thrust = 3e4;
以下はシンボリック式からmatlabFunctionコマンドによって実際に生成したMATLAB関数コードの1つです。
function f = landerStateFcn(in1,in2,Q,Qn,R)
%landerStateFcn
% F = landerStateFcn(IN1,IN2,Q,Qn,R)
% This function was generated by the Symbolic Math Toolbox version 9.3.
% 2024/03/07 18:32:52
T = in2(1,:);
ita1 = in2(2,:);
ita2 = in2(3,:);
m = in1(13,:);
p = in1(10,:);
phi = in1(7,:);
psi = in1(9,:);
q = in1(11,:);
r = in1(12,:);
theta = in1(8,:);
u = in1(4,:);
v = in1(5,:);
w = in1(6,:);
t2 = conj(T);
t3 = conj(ita1);
t4 = conj(ita2);
t5 = cos(phi);
t6 = cos(psi);
t7 = cos(theta);
t8 = sin(phi);
t9 = sin(psi);
t10 = sin(theta);
t11 = tan(theta);
t15 = u.^2;
t16 = v.^2;
t17 = w.^2;
t18 = 1.0./m;
t12 = cos(t4);
t13 = sin(t3);
t14 = sin(t4);
t19 = t15+t16+t17;
t20 = sqrt(t19);
t21 = conj(t20);
mt1 = [-v.*(t5.*t9-t6.*t8.*t10)+w.*(t8.*t9+t5.*t6.*t10)+t6.*t7.*u;v.*(t5.*t6+t8.*t9.*t10)-w.*(t6.*t8-t5.*t9.*t10)+t7.*t9.*u;-t10.*u+t7.*t8.*v+t5.*t7.*w;-q.*w+r.*v-t6.*t7.*3.721-t18.*t21.*conj(u).*1.289405600688818e-1+t2.*t12.*t18.*cos(t3).*9.3025e+6];
mt2 = [p.*w-r.*u+t5.*t9.*3.721-t18.*t21.*conj(v).*2.090665-t6.*t8.*t10.*3.721-t2.*t12.*t13.*t18.*9.3025e+6;-p.*v+q.*u-t8.*t9.*3.721-t18.*t21.*conj(w).*2.090665-t5.*t6.*t10.*3.721+t2.*t14.*t18.*9.3025e+6;p+q.*t8.*t11+r.*t5.*t11;q.*t5-r.*t8;(q.*t8+r.*t5)./t7;0.0];
mt3 = [p.*r.*9.907930069717351e-1+t2.*t14.*2.339286561771103;p.*q.*(-9.907930069717351e-1)+t2.*t13.*2.339286561771103;T.*(-7.183908045977011e+3)];
f = [mt1;mt2;mt3];
end
補足として、in1が状態、in2が入力として対応しています。
またQ、Qn、Rは、それぞれ評価関数における各項の重みに関する追加パラメーターとなっています。
重みのパラメーターは状態関数の計算に直接関係がありませんが、非線形モデル予測制御(NMPC)の設計においては、ツールの制約上、外から追加で与える調整可能な任意パラメーターはすべての関数に入力引数として与えておくことが必要になります。
詳細は以下のヘルプにて。
詳細なロケットの物理モデル
前章までで、ロケットの運動を表現する運動方程式が生成できました。
これは後程、MPCの予測モデルとして扱っていくのですが、これとは別にシミュレーションのためのプラントモデル(制御対象)が必要となります。
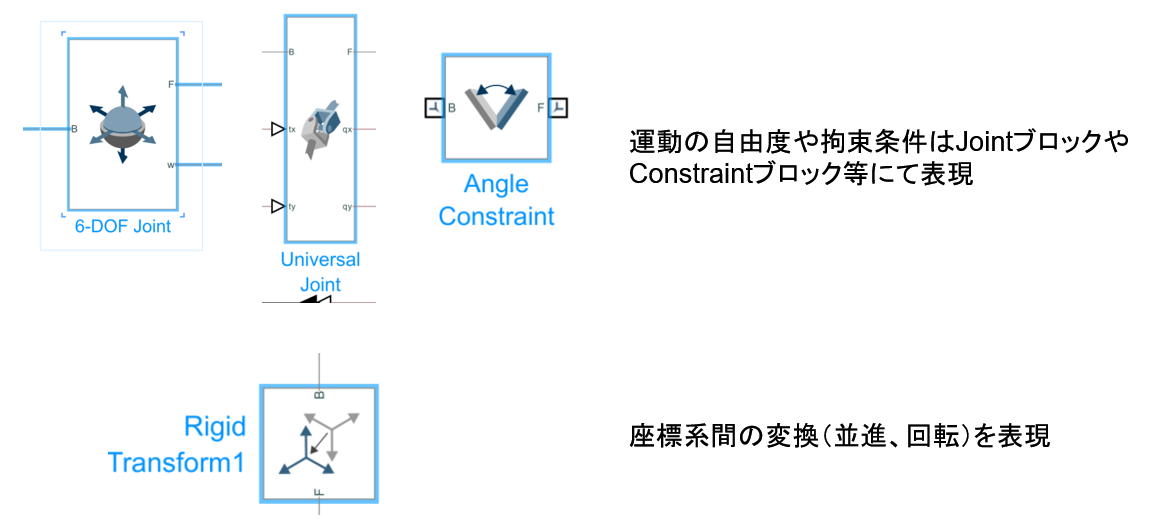
通常は、生成した式のモデルをそのままプラントモデルとしても扱っても良いのですが、ここではより詳細な物理モデルで構築することを前提とし、物理モデリングツールであるSimscape、Simscape Multibodyを使って下図のようにモデリングしておきます。

ここでSimscape Multibodyは、3Dの機構モデルを設計するための物理モデリングツールであり、形状指定(CADからの取り込みもサポート)、運動の自由度や拘束、接触の定義等をモデル化することが可能となっています。


特に接触の定義では、Spatial Contact Forceブロックというものを使って、ブロックに入力する基準軸(B:ベース)と相対軸(F:フォロワー)間の個体同士の接触力を計算します。
なお、接触の計算では下図のように凸包(Convex hull)に基づいて行われます。

画像出典:https://jp.mathworks.com/help/sm/ref/spatialcontactforce.html
今回は各着陸脚の先端面と地面との間に接触を定義し、接地時に地面を貫通しないようにしておきます。
出来上がったモデルはMechanics Explroresという機能にて3Dのアニメーションで表示させることが可能です。

導出した数式のモデルとSimscapeによる詳細モデルとの差異をシミュレーションによって確認してみます。
比較シミュレーションでは下図のように各モデルに対し、同じ入力をインプットした際の応答を確認します。

次の図は10秒間のシミュレーションを行った際のトレンド結果です。
なお、この際のテスト入力としては、ゆっくりと機体を降下させつつ、推力偏向によって角度変化を生じさせるような運動を模擬しています。

各状態量について、青線が数式、緑線が詳細モデルの結果となりますが、概ね波形の傾向が一致しているもののズレがあることが分かります。
このズレはモデル化に伴う誤差であり、モデル化誤差と呼ばれるものになります。
制御系設計では、このように実機(今回はすべて机上のモデルですが。。)とのモデル化誤差が伴うのが必然です。
そのため、誤差に対してロバストな制御系を構築することが必要となってきます。
非線形モデル予測制御による着陸制御系の構築
それでは、着陸制御のためのコントローラーをMPCの一種である非線形モデル予測制御(NMPC:Nonlinear MPC)を使って設計していきたいと思います。
今回もコントローラー開発には、Model Predictive Control Toolboxを使っていきます。
設計は前回の記事のものを踏襲した形となっていますが、大きく異なる点としては、①質量の制約を考慮している、②着陸に関する非線形な不等式制約を考慮している点があります。
①に関しては、ロケットの質量のおよそ30%が燃料(wet mass)であり、残りが機体の構造に関する質量(dry mass)と仮定しています。
そのため、質量は下限制約(dry mass)を物理的に逸脱できないように制約を与えています。
こうすることで、NMPCは常に質量が下限以上となるように制御を行うため、燃料の有限性を考慮した最適化を行ってくれるはずです。
なお、万が一燃料が空になった場合は、エンジン推力が発生できなくなりますが、その影響はプラントモデル側で考慮します。(制御としては実行不可能な状態)
②に関しては、着陸ポイントに精度良く誘導するため、下図に示すような着陸ポイントである慣性系の原点を頂点とするグライドスロープを引き、スロープによって形成される円錐面に対して、機体が常にその面内に位置するように制御することを制約条件として与えます。

以下がNMPCの設計スクリプトです。
Ts = 0.6;
lander = nlmpc(13,13,3);
lander.Ts = Ts;
p = 12;
m = 2;
lander.PredictionHorizon = p;
lander.ControlHorizon = m;
% Model
lander.Model.StateFcn = 'landerStateFcn';
lander.Jacobian.StateFcn = 'landerStateJacobianFcn';
% Custom Cost Function
lander.Optimization.CustomCostFcn = 'landerCostFunction';
% Custom Constraints
lander.Optimization.CustomIneqConFcn = 'landerIneqConFunction';
% Thrust Power [pu]
lander.MV(1).Min = 0;
lander.MV(1).Max = 1;
% Gimbal1 angle [rad]
lander.MV(2).Min = -10*pi/180;
lander.MV(2).Max = 10*pi/180;
lander.MV(2).RateMin = -100*pi/180*Ts;
lander.MV(2).RateMax = 100*pi/180*Ts;
% Gimbal2 angle [rad]
lander.MV(3).Min = -10*pi/180;
lander.MV(3).Max = 10*pi/180;
lander.MV(3).RateMin = -100*pi/180*Ts;
lander.MV(3).RateMax = 100*pi/180*Ts;
% OV physical limits
% x
lander.OV(1).MinECR = 0;
lander.OV(1).Min = L/2;
% Mass
lander.OV(13).Min = dry_mass;
lander.OV(13).MinECR = 0; % Hard constraint
% Scaling Factor
lander.States(1).ScaleFactor = 100;
lander.States(2).ScaleFactor = 100;
lander.States(3).ScaleFactor = 100;
lander.States(4).ScaleFactor = 10;
lander.States(5).ScaleFactor = 10;
lander.States(6).ScaleFactor = 10;
lander.States(7).ScaleFactor = 10*pi/180;
lander.States(8).ScaleFactor = 10*pi/180;
lander.States(9).ScaleFactor = 10*pi/180;
lander.States(10).ScaleFactor = 10*pi/180;
lander.States(11).ScaleFactor = 10*pi/180;
lander.States(12).ScaleFactor = 10*pi/180;
lander.States(13).ScaleFactor = mass;
lander.ManipulatedVariables(2).ScaleFactor = 10*pi/180;
lander.ManipulatedVariables(3).ScaleFactor = 10*pi/180;
% Weights for cost function
Q = diag([50 50 50 5 5 5 0 2 2 0 1 1 0]); % Stage cost of state
Qn = 10*diag([100 100 100 10 10 10 0 2 2 0 1 1 0]); % Terminal cost
R = diag([2 .1 .1]); % Stage cost of input
% Number of optional parameters
lander.Model.NumberOfParameters = 3;
function cineq = landerIneqConFunction(X,U,e,data,Q,Qn,R)
% X:states
% U:inputs
% e:slack variable
% data:structured parameters
% Q,Qn,R:additional parameters (weights)
% Nonlinear inequality constraint about Glide Slope
x = X(:,1);
y = X(:,2);
z = X(:,3);
glide_slope_angle = 20*pi/180; % Glide slope angle
cineq = sqrt(y.^2 + z.^2)*tan(glide_slope_angle)-x;
end
ここでNMPCによる制御周期は、計算コストを考慮して0.6[s]とし予測ホライズンは12ステップとして、7.2[sec]先までの応答を予測しながら実時間で最適化問題を解いていく設定とします。
また評価関数の各重み(Q、Qn、R)はシミュレーションを通じて試行錯誤によって調整した結果です。
シミュレーション
それでは、設計したNMPCのコントローラーを使って着陸制御のシミュレーションを行ってみたいと思います。
閉ループのシミュレーションモデルは下図のような構成となっています。

ここで、Landing Controllerサブシステムが着陸制御のためのコントローラーです。
本サブシステムの内部は、下図に示すようにStateflowのChartブロックを利用しており、イベントドリブンで制御のモードが切り替わるようなスケジューラーを組んでいます。

Chartブロックの内部では、Simulinkのサブシステムをステートとして呼ぶためのSimulinkステートという機能があるので、これによって着陸制御がEnable(ON)時とDisable時(OFF)で出力される内容を切り替えるように構成しています。
さて、シミュレーションではロケットが火星の大気圏に突入し動力降下を開始している最中で所定の高度からNMPCによる制御によって最終的な着陸フェーズに移行するというようなシナリオを考えたいと思います。
そのため、以下のような初期条件を与えます。
% Initial values
euler0 = [0 -80*pi/180 0];
% Position
px0 = 1000;py0 = -100;pz0 = -100;
% Velocity
Ve0 = [-100 0 0]; % Velocity @ inertia axis
Vb0 = dcmbe(euler0)*Ve0'; % Velocity @ body axis
u0 = Vb0(1);v0 = Vb0(2);w0 = Vb0(3);
% Attitude
phi0 = euler0(1);theta0 = euler0(2);psi0 = euler0(3);
% Angular velocity
p0 = 0;q0 = 0;r0 = 0;
また外乱としてランダムな突風を想定します。
火星は空気密度が地球の100分の1とかなり薄いのですが、年間の平均風速10[m/s]と地球と比較しても高いことがこれまでの観測で分かっています。
そのため、風による影響は少なからず発生するため、リスクを考慮して評価することが必要です。
それでは、以下にシミュレーション結果ならびにその際のアニメーションを示します。


結果から分かる通り、最初に機体の大きな姿勢変化を伴いながらも最終的には良好に着陸地点に向けて転回し誘導できていることが分かります。
アニメーションには地面に着陸地点を中心とした半径10[m]四方のマーキングを書いているのですが、機体はその領域内で接地していますので非常に高い精度で制御されていると言えるかと思います。
加えて、アニメーションではグライドスロープによる円錐も途中の高度まで表示していますが、機体は常にこの範囲に収まっていることが分かります。
トレンドにおいて特筆すべき点としては、質量変化がかなり大きく生じていることです。
制御開始時は500[t]であった質量が、推力による燃料消費によって最終的には400[t]程度にまで減少しています。
約20%強の質量変動が起こっている計算になりますが、NMPCはこの変動に対してロバストに制御できています。
以下のアニメーションにて質量変動に伴う重心位置の変化を表示しています。
その他、気象の影響として突風外乱も考慮しているのですが、風に流されることなく安定に制御できていることも分かります。
この時の入力の結果を見てみると、すべて指定した制約の範囲内で収まっていることが分かるので問題ありません。
以上の評価から、今回のモデルに対し、NMPCは優れた制御性能を達成できていると結論づけられるかと思います。
最後に
今回はロケットの着陸制御 第2弾として、前回よりももう少し踏み込んだ検討を行ってみました。
NMPCの予測モデルを生成するためにSymbolic Math Toolboxを利用しましたが、シンボリックな変数から数式の定義ならびに偏微分操作なども行えるので、スムーズにモデル構築を行うことが可能です。
余談ですが、開発が進むStarshipは2024年の3月14月に3回目の軌道打ち上げ試験が行われ、第1段ロケットであるSuper Heavy及び第2段のStarshipのエンジンすべてが正常に燃焼し、予定されていた軌道への到達、Super HeavyとStarshipの切り離し、Super Heavy帰還のためのブーストバック飛行などなど様々なマイルストーンを達成しました。
切り離し後のStarshipはサブオービタル飛行を続け、その間ラプターエンジンの再着火や燃料移送、ペイロードドアの開閉といった様々なテストを試みていたようです。
最終的に大気圏への再突入を試みましたが、姿勢制御に問題があったようで所定よりもロールレートが大きく、その影響によるものか定かではありませんが、再突入で発生する空力加熱に機体が耐え切れず消失しました。[1][2]
再突入に至る様子はオンボートのStarlink端末によってLive配信され、まるでSF映画のような圧巻の映像となりました↓
今年も宇宙に関する話題がアツい年になりそうですね🚀
参考情報
[1] https://news.infoseek.co.jp/article/sorae_129376/
[2] https://news.yahoo.co.jp/articles/79bc02d101a7a7607f5d0bf6cc7c68dfbf860011?page=2