はじめに
巷では、三菱重工のMSJ(三菱スペースジェット)の事業撤退という残念なニュースがありましたね。
得られた知見や開発ツールは次世代戦闘機開発に生かすということのようなので、ぜひ頑張って頂きたいです。
というわけで、前回に引き続き航空機の飛行制御を題材にトピックを書いてみようと試みています。
前回の記事↓
今回取り上げるのは自動着陸です。
自動着陸はILSという計器着陸装置を使用した自動制御の技術です。
ILSは、空港に侵入する航空機に機体の現在位置を知らせるための装置です。
通常、我々が乗るような旅客機は滑走路に対し、降下角-3°の姿勢を保って進入します。
ちなみに運用が終了したNASAのスペースシャトルは、帰還時にグライダーのように無推力で飛行して滑走路に着陸しますが、通常の航空機と比べて主翼面積が少なく、揚抗比(揚力÷抗力)が小さいので着陸時の降下角を-15°以上に保つ必要があったそうです。
かなり深い角度で進入するので、この急降下具合をクリント・イーストウッド主演のスペース カウボーイという映画では空飛ぶレンガだと揶揄されていました。
話を戻しまして、ILSは、この目標降下角と機体の現在位置に基づき、縦及び横の誤差を与えるローカライザならびに滑走路端からの距離を与えるマーカービーコンの構成の下、パイロットの着陸を支援します。
パイロットや制御装置は、このILSから送信される信号を受信することで適正な経路に対し機体がどれだけずれているかを認識し、適切に操舵を修正することが出来るという仕組みとなっています。

引用:国土交通省 https://www.mlit.go.jp/common/001264274.pdf より
ちなみにこの自動着陸ですが、常に使用されているという訳でもないようで、基本パイロットの技量維持のために手動での着陸機会が多いそうです。
しかし、条件によっては自動着陸の方が推奨される気象条件や空港などもあるそうで、パイロットは適切に判断して使い分けているということのようです。
というわけで今回は航空機の着陸制御に焦点をあててシミュレーションによる評価を行ってみたいと思います。
プラントモデル
シミュレーションにはSimulinkを使っていきますが、制御対象となるプラントモデルは、前回の記事同様にAerospace Blocksetを利用してB747の6自由度の飛行シミュレーションモデルを組んでおきます。

上図のようにAerospace Blocksetには剛体の6自由度の非線形運動を定義するためのブロックが提供されている他、重力や標準大気、風外乱などブロックも提供がありますので飛行環境の構築をスムーズに行うことが可能です。
自動着陸のための誘導制御系の構築
機体を与えられた軌道に追従させるためには、機体の並進運動と回転運動を適切に制御することが必要です。
一般に航空機の飛行制御では、並進に関する制御を誘導(Guidance)と呼び、目標となる軌道の生成ならびにそれに沿って飛行するために必要となる機体の目標姿勢角を生成します。
誘導系からの目標姿勢角を受けて回転に関する制御を行う系を制御(Control)と呼び、制御のための操舵量(制御入力)を生成します。
この誘導と制御を合わせて誘導制御(Guidance and Control)と呼称します。
またセンシングを司る航法(Navigation)も合わせると、航法誘導制御(GNC:Guidance, Navigation and Control)と呼ばれるようになります。
基準軌道の設計
今回は旅客機の着陸軌道(グライドスロープ)となるため、冒頭で記したように滑走路端から-3[deg]の降下角を持つ軌道を引きます。
ただし、-3[deg]の降下角で直線上に降下していくと最終的には地面に衝突してしまうので、所定の高度に達したらフレアと呼ばれる機体の引き起こし操作を行い、小さな沈下率(Sink rate)でタッチダウンします。(下図)
この基準軌道の設計はSimulinkを使って下図のようにSwitchブロックとEnabled Subsystemブロックによって実装されています。
Switchブロックは高度を見てグライドスロープとフレアの切替制御を行っています。
フレアの軌道は時定数で指数関数状に減少していくように決定されます。$^{[1]}$
機体の横位置の軌道に関しては、常に滑走路の中心線上に位置するように制御するため、0[m]で一定として扱います。
以上がILS相当のシステムとしてモデルに組み込んでいきます。
誘導制御系の設計
続いて、前節で与えられた基準軌道に追従するための誘導制御系をカスケードのPID制御で構築していきます。
航空機の運動は、操舵を通じて、角速度ー>角度ー>速度ー>位置という順に変化していきます。
制御工学的に言えば、タイムスケールで分割できるため、今回のようにカスケードなループ構成(運動の順序とは逆に辿って、位置ー>速度ー>姿勢ー>角速度ー>操舵量の順で制御を求める)が取られる場合があります。
具体的には、縦に関する誘導制御の場合、基準軌道から与えられる高度と現在の機体高度との偏差に基づき、PID制御によって沈下率の目標値が作られ、そこからピッチ角、ピッチ角速度の目標値となり、最終的にエレベーター舵角(de)の指令が作られます。
なお、沈下率の制御では基準軌道を時間微分することで得られる理想的な沈下率をフィードフォワード項として設け、2自由度制御の構成にし、軌道に遅れなく追従できるようにしています。
またエンジンの推力(dT)を用いて機体の進行方向の速度を制御しています。
横に関しては、横位置の制御から方位角、ロール角の制御を行い、最終的にエルロン舵角(da)の指令を作るのと同時に、機体の横滑りを抑える観点からヨーレートを0にするようにラダー(dr)の舵角指令を作っています。
今回は、各PID制御のゲインにおいてシミュレーションを見ながら手動での調整およびSimulink Control Designから提供されているPID調整器を利用しました。
チューニングのコツ
今回のようなカスケードループの場合、内側のループから順に調整していくと効率が良いと思います。
例えば、まずは一番内側の角速度の制御ループだけを閉じて、他の制御ループは開いてしまいます。
そして、角速度の目標値に任意の信号を注入して制御がうまくいくかを評価し、調整していきます。
ある程度角速度の調整がうまくいったら、今度は角度のループも閉じて同様にチューニングを行います。
これを速度、位置まで繰り返すとほどほどに性能が良い応答が得られることが多いです。
最終的には応答に対する感度の高いパラメーターに見当をつけて、全体の性能を仕上げていきます。
またPID制御の場合、筆者はまずはPゲインだけ、もしくは小さなIゲインを設定して初期評価を行い、そこからPの感度、Iの感度を見つつ、徐々に値を変えていきます。(最初はP=1、I=0.01くらい)
オーバーシュートや振動が気になる場合にはD制御も少し加えてみて抑制の効果があるかを見ています。
場合によってはI制御を加えると安定余裕がなくなるため、その場合はPD制御(制御対象に積分器がある場合)にしてみたり、PID以外に位相進み補償を入れて位相特性を改善することも必要だと思います。
自動着陸のシミュレーション
それでは、自動着陸のシミュレーションを行っていきます。
機体は滑走路端(慣性座標の原点)からX軸方向にー10000[m]、Y軸方向に100[m]、高度500[m]に位置するとして、自動着陸を開始します。
なお、飛行中は突風外乱(Dryden Model)を考慮します。

図 機体の沈下率及び姿勢角の結果

図 考慮した突風外乱のトレンド
以上の結果から風の影響を受けても上手く制御できていることが分かります。
特に最初に大きく左にバンクして機首の向きを変えています。こうすることで機体を滑走路の中心線上に制御しています。
またピッチ角を見てわかる通り、グライドスロープにのっている間は-3[deg]付近で姿勢を保ちながら飛行し、タッチダウン直前にフレアによる機首上げを行っていることが見て取れます。
また沈下率もフレア操作によって小さな値になっています。
モンテカルロシミュレーション
先ほどのシミュレーション結果は無数にある飛行シナリオの内の1つを抽出し、検証したにすぎません。
実際には様々な不確定事象が飛行中に発生し得るため、飛行制御系はそれらに対しロバストである必要があります。
実際の飛行機を飛ばして検証できれば一番でしょうが、著者は平凡な一市民であり財力も機材もリソースも、まして権限もございません笑
そのため、数値シミュレーションを使って、変動し得るパラメーターを乱数で振って繰り返しシミュレートすることでシステムの信頼性を評価することが必要になってきます。
そのような時に行うのがモンテカルロシミュレーション(MCS:Monte Calro Simulation)です。
実際、実機を使ったテストが難しい航空宇宙分野では、MCSでシステムの評価を行うことが主流となっています。
それでは、構築した誘導制御系の信頼性を評価するためにMCSを行いたいと思います。
今回MCSによってランダムに振るパラメーターは以下の通りとします。
ここで、各パラメーターはその母集団特性(真なる特性の集合)がある統計分布に基づいていると仮定し、その中から無作為に抽出されるとします。
統計分布はパラメーターの特性や取り得る値の確率値に基づき、正規分布や一様分布などを使って評価します。
さて、このMCSですが、モデルを使って繰り返しシミュレーションを回していきます。
一般にMCSは母集団特性からの標本抽出の作業になるので、少ないサンプル数(=シミュレーション回数)では、統計的に信頼性が保てない可能性があります。
ゆえに、数百~数万回と多くのシミュレーションを行わなければならないケースが生じます。
1回のシミュレーションが数秒オーダーで終わるならば良いのですが、場合によっては数分、数時間とかかってしまうケースもあるため、可能な限りPCのリソースを使って並列・分散で回していくことが必要になってきます。
MATLABの製品ファミリーであるParallel Computing Toolboxでは、マルチコアCPUを積んだPCやGPU環境における並列計算、ならびにサーバーマシンでの分散処理を支援する機能があります。
この製品の機能を利用することでSimulinkの複数回のシミュレーション実行を行うparsminというコマンドにて並列計算を行うことが出来るようになります。
% parsimを用いたモンテカルロシミュレーション
mdl = 'ILS_approach'; % Simulinkモデル名
rng('default') % 乱数のシード設定
sample = 200; % MCSの実行回数
% 各パラメーターの初期値
Xe0 = [-10000 100 -500];
euler0 = [0 0 0];
% 初期位置に関するサンプル生成
sigma_Xe = [1000 100 30];
Xe_d = (2*rand(sample,3) - 1).*sigma_Xe+Xe0;
% 初期角度に関するサンプル生成
sigma_euler = [1 1 1].*pi/180;
euler_d = (2*rand(sample,3) - 1).*sigma_euler+euler0;
% 突風の強さに関するサンプル生成
sigma_windMag = 5;
windSpeedatSixMeter_d = rand(sample,1)*sigma_windMag;
% 突風の向きに関するサンプル生成
sigma_windDir = 360;
windDirectionatSixMeter_d = rand(sample,1)*sigma_windDir;
% SimulationInputオブジェクトを利用して各実行シナリオを定義していく
for i = sample:-1:1
in(i) = Simulink.SimulationInput(mdl);
% setVariable関数を利用してモデル内の各パラメーターを生成したサンプルの値で置換していく
in(i) = in(i).setVariable('Xe0',Xe_d(i,:));
in(i) = in(i).setVariable('euler0',euler_d(i,:));
in(i) = in(i).setVariable('windSpeedatSixMeter',windSpeedatSixMeter_d(i,:));
in(i) = in(i).setVariable('windDirectionatSixMeter',windDirectionatSixMeter_d(i,:));
end
% parsimで実行開始
out = parsim(in,'ShowProgress','on','TransferBaseWorkspaceVariables','on','ManageDependencies','on');
モデル上で特定の信号線をログ設定しておくと、各実行における結果がout引数として専用のデータオブジェクトに格納されて返ってきますので、各データにアクセスしてデータ処理することが可能です。
実際、以下に200回のMCSを行った結果をplotしていきます。

図 200回の飛行軌道の鳥瞰図
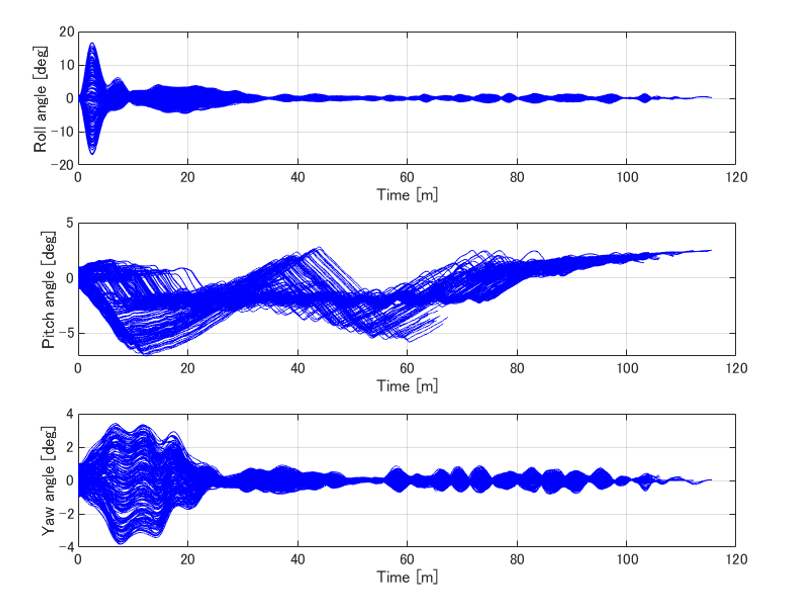
図 200回の姿勢角のトレンド図

図 着陸時の各評価量
いかがでしょうか。飛行軌道を見ると結構ばらついていることが分かります。
特に高度がうねうねしていますね。よく見ると滑走路の端(Downrange = 0[m])に到達する前に着陸?墜落?しているケースがあるようです。
姿勢角のトレンドを見るとやはりピッチ角が大きく振動しています。
3つ目の図は着陸時(接地時)の状態をプロットしたものです。
ここで赤い枠線がありますが、機体の各状態が着陸時にこの枠内にあれば着陸成功だと評価しています。
左上の図を見てみると、いくつかのケースはやはり滑走路に到達する前に接地していそうです。
右上の図はロール角、ヨー角の状態を示していますが、0[deg]付近に収まっているので横に関する姿勢の異常はなさそうです。
下の図はピッチ角と沈下率に関する結果ですが、いくつかのケースでは沈下率が規定値(3[m/s])を上回るスピードとなっており、かつピッチ角が降下角-3[deg]以上となっているので、フレアによる引き起こしができていないことが分かります。
要するに墜落していますね。。
全体の失敗回数を集計すると、200回の飛行中に着陸に失敗するケースは計32回でした。
確率に換算すると、失敗する確率が16%(=32/200)もあることになります。
これでは安心して自動制御に任せられないですね。。。
感度解析評価
制御がダメでしたという終わり方では締まりが悪いので、制御屋として何が悪かったかをきちんと分析して、性能アップに頑張って繋げたいと思います。
そこで、もう一度MCSを行います。
ただし、同じことを繰り返すのではなく、結果を集計して統計分析に基づき、何がリスクになるパラメーターなのかを割り出していきます。
実際、このような研究は以前から行われています。
MATLABの製品ファミリーであるSimulink Design Optimizationでは、この感度解析を支援してくれる機能が提供されています。
それが感度アナライザーと呼ばれるアプリです。
感度アナライザーはSimulinkのアプリタブ内から起動することが出来ます。
アプリを起動すると↓のようなGUIが起動します。
各アイコンで設定していく手順を①~④で簡単に図示しています。

②における指定項目ですが、下図のようになっています。
リストには①で指定したモデル内で使用されているパラメーターが表示されており、各々の分布とその統計的特性を指定したらOKボタンを押します。

そうすると、下図のように指定したサンプル数分だけ変動パラメーターの組み合わせが生成されます。
これがMCSで評価するパラメーターセットとなります。

続いて、③にてMCSで評価する際の要件を指定します。
今回で言えば、着陸時の状態が該当します。
下図では、モデル上のX方向の位置に相当する信号について、その最終値(接地してシミュレーション終了となるようにしている)が0以上となるように要件を指定します。(要するにX(end)>0、Xは時系列信号)
今回は、これ以外にも沈下率に関する要件を指定しておきます。(Zdot(end)<3、Zdotは時系列信号)

以上ですべての設定が完了したので、④のモデル評価を実行してMCSを開始します。
下図はMCS終了後の各変動パラメーター(横軸) vs 要件(縦軸)の散布図を示しています。
すべて 要件 ≦ 0 となるように整理されているようですので、X(Downrange)については負の値が要件を満たしているケース、沈下率(sink rate)も同様に負の値となっているものが要件を満足するケースと読み取れます。
散布図を見ると、どうやらXe0(1)とXe0(3)について要件の偏りがあるため、各々有意な相関がありそうです。
ちなみにこれらはX軸の初期値と高度の初期値のパラメーターです。

以上で得られた結果について統計処理を施して、因子となるパラメーターの特定を行ってみたいと思います。
アプリの統計タブをクリックすると、MCSの評価結果についていくつかの回帰や相関、ランク付けなどの統計メソッド及びタイプに基づき、トルネードプロットを表示してくれます。
筆者は統計学が専門ではないのですが、とりあえず全部選択してみて結果を見てみようと思います。
トルネードプロットは各要件に対し、リスクの度合いが大きい順に因子を並べた図です。
結果を見るとX方向の位置ならびに沈下率の要件ともに1位,2位で同じパラメーターが複数の指標でレポートされています。
これらは先ほどの散布図でも視認されたXe0(1)とXe0(3)です。
図中の横軸は0を境に相関の符号とその度合いを示しています。
Downrangeについて見てみると、Xe0(1)すなわちスタート時のX方向の位置が要件に対して正の相関を持っています。
これの解釈するところとして、機体がグライドスロープに乗る位置が滑走路方向に詰まると墜落しやすい傾向となることを意味しています。
確かに、グライドスロープのラインから前方にオフセットした状態でスタートすると、下図のように機体が降下角-3[deg]のラインの上に位置することになるので、制御開始と同時に深い降下角と大きい沈下率で追従しなければなりません。
しかし、現在の制御器ではそれほど機敏に機体を制御できないため、フレアにおける引き起こし操作が間に合わず墜落していると考えることができます。
Xe0(3)もスタート時の高度(h0 = -Xe0(3))に関するパラメーターです。
要するにグライドスロープに乗る際の機体の縦方向の位置のバラつきに対して、今の制御器はロバストではないという考察がまとまります。
では、実際にそうなのか検証するために、洗い出したXe0(1)とXe0(3)のパラメーター変動がない、すなわち適切な開始位置で常に一定と仮定した状態でMCSの再評価を行ってみます。
以下がその結果です。

図 200回の飛行軌道の鳥瞰図

図 200回の姿勢角のトレンド

図 着陸時の評価量(ロール角、ヨー角の図は問題ないので省略)
いかがでしょうか。結果を見るとすべてケースでうまく着陸できています。
飛行中の姿勢角も問題ありませんし、着陸時も所定の制限値を守っています。
失敗回数も驚異の0回という結果でした。
なるほど、高度を制御しているPIコントローラーをもうちょっと改善する余地がありそうです。
ロバストチューニング
リスクのある変動パラメーターの洗い出しと調整するパラメーターの方針が整いました。
では、PIコントローラーのパラメーターを変えながらMCSで評価して、ダメだったらまた変更してMCSで評価して。。。とやっていると時間掛かってしまいます。
よって、最適化によって効率よくチューニングしていきたいと思います。
そのために使用できるツールが、同じくSimulink Design Optimizationから提供されている応答オプティマイザーというアプリです。
以前の記事でも機能の紹介をしていますので興味のある方はどうぞ↓
実はこの応答プティマイザーは感度アナライザーと連携することが出来ます。
どういうことかというと、感度アナライザーで生成したパラメーターセットを利用して、不確かなパラメーターを考慮した応答最適化を応答オプティマイザーで行うことが出来ます。
以下に図を利用して手順を示します。
以上で設定が完了したら、オプションで利用する最適化ソルバーを選択し、Parallel Computing Toolboxの機能で並列計算させる場合には設定するなどしたら、最適化のボタンを押すだけで計算が始まります。
なお、今回は最適化ソルバーとして逐次2次計画法(SQP)を利用しました。
大体1時間で最適化が収束しました。
モデルの規模や利用する最適化のソルバーによって計算時間は変わります。
また並列化したからといって常に計算時間が短縮されるというわけでもありません。
並列ワーカーとの通信のオーバーヘッド等、様々な要因によって並列化のメリットが活かせないケースがあり得ます。
PIゲインの結果を確認すると最適化によって以下のようになりました。
最適化によって、Pゲインは-43%小さくなり、一方でIゲインは165%大きくなりました。
どうやらIゲインを大きくすることで軌道への追従性を向上させているようです。
それでは、この結果を用いて、当初の変動パラメーターを考慮したMCSを行ってみましょう。

図 200回の飛行軌道の鳥瞰図

図 200回の姿勢角のトレンド

図 着陸時の評価量(ロール角、ヨー角の図は問題ないので省略)
結果を見ると1つのケースを除き、着陸がうまくいっていることが分かります。
失敗した1ケースは、滑走路の上限を超過していました。(今回は滑走路の上限は最適化で評価していません)
しかし、成功確率としては99%以上ということでかなり高い信頼性を有しています。
これなら制御に任せても良いかなと思えそうですね。
最後に
Aerospace Blocksetから提供されているPilot Joystickブロックを利用して、ゲームパッドからパイロット気分になって手動着陸を試みてみました。
(アニメーションは6倍速)
結果は、、、着陸する前に機体を放棄しました苦笑
時折、突風が吹いて機体の姿勢が大きく崩されます。これがウィンドシアというやつですね。
またアクチュエーターの応答速度や機体の大きな慣性によって遅れがかなりあるため、姿勢を戻そうとしても振動してしまい、操縦がかなり難しいと感じました。(PIO:Pilot-Induced Oscillation という現象)
エアラインのパイロットは台風のような強風の中でも着陸することがありますが、改めてその技量の凄さが分かりました。
参考文献
[1]嶋田 有三、佐々 修一 著:飛行力学, 森北出版株式会社
[2]元田 敏和、塚本 太郎、南 吉紀、濱田 吉郎 著:宇宙航空研究開発機構研究開発報告 リフティングボディ飛行実験(LIFLEX)誘導制御系 ーシステム評価と飛行制御パラメタ最適化ー, JAXA-RR-10-007.





















