はじめに
皆さんは耐故障(Fault Tolerant)という言葉を知っているでしょうか?
意味はその名の通り、故障に耐えることです。
例えば、航空機が飛行中に制御舵面、翼などに構造的なダメージを負う、またはアクチュエーターに故障が発生するとします。
この場合、オートパイロットは機体を安定化できるでしょうか?
仮に、オートパイロットがPID制御などの従来的な固定補償器で設計されている場合、これらは故障がないノミナルな状態に対して要求されるパフォーマンスを満足するように設計ならびに調整がされてることが一般的であるため、故障というイレギュラーな状態が発生すると閉ループの安定性を著しく損なう可能性が考えられます。
(おそらくパイロットはオートパイロットを切るでしょう)
実際、過去に発生したいくつかの航空機事故では、機体システムの故障が起因となっているものがあります。
ドローン等の無人機ならばともかく、多くの人が利用する旅客機では人命を優先し、安全第一でシステムが設計されていなければなりません。
こうした背景から制御によって落ちない飛行機を作るということをテーマに各種機関や企業にて様々な研究ならびに技術検証がなされてきました。
一般に耐故障制御と呼ばれるこのシステムでは、故障検知に加え、ロバスト制御や適応制御のアプローチが主に研究対象となっていましたが、近年はニューラルネットワークなどの機械学習ベースのアプローチも研究されてきています。
そこで、今回は航空機の耐故障制御 (FTC:Fault Tolerant Control)をテーマに一つ考えてみたいと思います。
耐故障制御としての適応制御
適応制御(Adaptive Control)とは、制御対象であるシステムの特性が未知な場合において、その特性を直接/間接的に推定しながら制御を行う制御手法です。
下図は適応制御の中でも代表的なモデル規範型適応制御(MRAC:Model Reference Adaptive Control)という制御系の模式図です。

図を見てわかる通り、MRACの特徴は、一般的なフィードバック制御系(制御対象と制御器)以外に規範モデルおよび適応機構というものが加わる点にあります。
ここで規範モデルとは、閉ループの理想的な応答特性を示す理想モデルです。
例えば、とある制御にて、出力の応答性を時定数がT秒の1次遅れに合致させるように調整、制御することを考える場合、この1次遅れが制御にとっての規範モデルとなります。
続いて、適応機構は規範モデルへの応答の追従制御に際し、プラントの未知なパラメーターを推定したり、制御のパラメーターをオンラインで逐次修正する働きがあります。
すなわち、適応制御は制御中に何か未知な変動が加わってもオンラインで適応的に対処することが期待できる制御ということになります。
実際に先行研究のいくつかは、耐故障制御として単純適応制御(SAC:Simple Adaptive Control)という適応制御の一種を用いた検討が行われています。
単純適応制御を用いた航空機の重心後退時における耐故障飛行制御に関する研究
今回は文献[1]を参考にSACによるピッチ角制御のFTCを設計していきたいと思います。
制御対象
まずピッチ角制御の対象となるモデルを導出する必要があります。
ここでは、以前の記事で登場したことのあるB747のプラントモデルを用いることとし、6自由度の非線形運動モデルからSimulink Control Designの線形化機能を利用して、線形近似モデルを導出します。
線形化機能の詳細は過去の記事をご覧ください。

上図の通り、B747の非線形プラントモデルの信号線上に線形化ポイントを置いています。
これで入力であるエレベータ舵角から出力であるピッチ角までの線形モデルをモデル線形化器を使って機械的に導出することが出来ます。
今回は機体の自動着陸時における飛行形態を想定し、高度530[m]、時速290[km]におけるトリム飛行状態での線形近似モデルを導出します。

linsys1という名前で得られた線形近似モデルですが、一部に極零相殺があったのでminrealコマンドで最小実現にしておきます。
そうすると以下の伝達関数モデルが得られました。
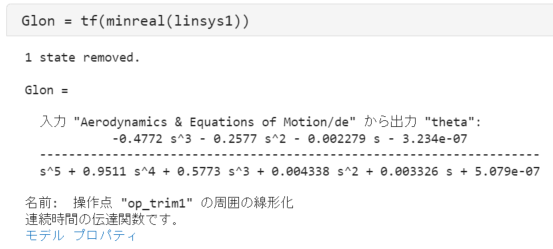
Glon = tf(minreal(linsys1))
確認すると分子分母にオーダーの非常に小さい定数項があるのが分かります。
これは0と捉えて問題ないと考え、以下のように手動で省いておきます。
[num den] = tfdata(Glon,'v'); % 伝達関数のnum,denの係数値をベクトルで取得
num = num(1:end-1); % 最後の要素以外を代入し直す
den = den(1:end-1); % 最後の要素以外を代入し直す
Glon = tf(num,den); % 伝達関数を定義
定数項を省いたことで分子分母の次数が下がり、最終的には以下のようになりました。
G_{lon} = \frac{-0.4772s^2-0.2577s-0.002279}{s^4+0.9511s^3+0.5773s^2+0.004338s+0.003326}
上記がエレベータ舵角からピッチ角までの伝達関数となります。
ここで、飛行力学を持ち出すと機体縦運動の極には大きく2つのモード、短周期モード、長周期モード(フゴイドモード)というものがあることが分かっています。
実際に極零点をpzmapコマンドでプロットしてみると以下のようになりました。

極配置を見ると短周期モードは固有振動数、減衰ともに大きいモードであるため早くに収束する一方、長周期モードは固有振動数、減衰ともに小さい極であるためゆっくりとした振動モード極であることが分かります。
実際にインパルス応答をimpulseコマンドによって計算してみると下図のようになりました。
impulse(Glon,1000)

理論的にも想定通りのモデルが得られているようです。
単純適応制御(SAC)
前節にて制御対象のモデルが得られたので、これを元にSACによるコントローラーを設計していきます。
冒頭にSACは適応制御の一種だと書きましたが、MRACを簡素化したような構成となっています。
実際、制御系のブロック線図は下図のようにいたってシンプルです。

SACは出力フィードバック制御に加えて、目標入力および規範モデルの状態量からのフィードフォワード制御を兼ね備えた2自由度制御の構えとなっています。
各ゲインを後述する調整則によって時々刻々と更新していくことで適応的な制御を実現していくわけです。
なお、SACを適用するにあたり、制御対象側の制約があります。
それは概強正実(ASPR:Almost Strictly Positive Real)であることです。
正実性の概念は、適応制御理論を学ばないと一般的な制御工学の教科書でも登場しないワードであるため、少し馴染みのない概念です。
ただし、SISOに限って言えば、ASPRとは以下の条件を満たす系を指しています。
・すべての零点が複素平面の左半面に存在すること(最小位相系であること)
・相対次数が0または1
・分子の最高位係数が正であること
では、このASPR性を満足する制御対象を考えた場合、かなり強い制約であり、SAC適用のハードルが結構高そうだということが分かってきます。
実際、今回のピッチ角の伝達関数を見てみると相対次数(分母と分子の次数差)が2であるので、この時点で要件を満足していないのでASPRではありません。
ではどうするのかというと、下図のように並列フィードフォワード補償器(PFC:Parallel Feedforward Compensator)というのを導入して、制御対象がASPRになるように拡大系を構成します。

要は、制御対象そのものは特性を変えることが出来ないので、制御側でちょっといじってやって、SACから見て対象の見かけの特性がASPRになるようにすれば良いんじゃないかという発想です。
ここで、多くの人は「じゃあ、どうやってPFCを設計すればASPRになるの?」と疑問が湧くと思います。(私も思います)
以下の参考書を見てみるとシステマチックにPFCを設計するためのアプローチがいくつか提案されてはいるようです。
が、ここではあまり深いことは考えず、先駆者の知恵を拝借し、文献[1]に記載の通り以下のPFCを適用することにします。
G_F = \frac{0.01}{s+1}
実際にPFCを適用したピッチ角の伝達関数の拡大系は以下の通りです。
Gf = tf(0.01,[1 1]);
Glon_aug = -Glon + Gf
G_{lon_{aug}} = \frac{0.01s^4+1.345s^3+2.546s^2+1.218s+0.01785}{s^5+2.59s^4+3.2s^3+1.63s^2+0.03068s+0.01044}
ここで、ピッチ角の伝達関数の負の符号を正に直しました。
この負符号は、エレベータ舵角が正(下げ舵)の時にピッチ角が負(機首下げ)という操舵と出力の間の関係性を表しています。
そのため、この負符号は、零点やシステムの安定性には影響を与えないので取り扱い上、無視してしまいます。
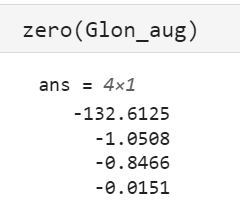
拡大系を評価すると、まず相対次数は1であるため要件を満足し、分子の最高位係数も正です。
零点を確認するとすべて安定(左半面に存在)ですのでこれも問題ありません。
よって拡大系はASPR性を満足しています。
zero(Glon_aug)
あとは、ゲインの調整則になりますが、これは以下の積分調整則を用います。
\dot{k}(t) = -e(t)z(t)^T\Gamma_{I} - \sigma_I k(t)
z(t) = {[e(t)^T,x_m(t)^T,u_m(t)^T]}^T
ここで、$e$は出力の追従偏差($y-y_m$)、$x_m$は規範モデルの状態量、$u_m$は目標入力であり、$\Gamma_I$が調整則のゲインです。
続いて、 $\sigma_I$が積分がバースト(発散)するのを抑制するためのシグマ修正項と呼ばれる項になり、任意の正の実数で表される調整項になります。
なお、上記調整則は、リアプノフ関数を用いて時間の経過とともに漸近安定であることが理論的には証明されています。
SACによるピッチ角制御(ノミナル)
それでは、まずSACによる制御によって、故障のないノミナルなピッチ角の制御を行ってみます。
制御対象は線形近似した$G_{lon}$を用います。
SACのSimulinkモデルは下図の通りです。規範モデルは1次遅れとしています。

今回エレベータ舵角としては±40[deg]の舵角制限があるものとして扱います。
閉ループの全体シミュレーションモデルは↓の感じ。

なお、SACのパラメーターは試行錯誤の末、以下の値としました。
Tm = 2; % 規範モデルの時定数(規範モデルは1次遅れ)
gamma_I = 1000*eye(3); % 積分調整則のゲイン
sigma_I = 0.001; % シグマ調整項
c0 = zeros(1,3); % 積分器の初期値
目標入力として±10[deg]のパルス状信号を与えたときのシミュレーション結果が以下の通りです。

図の1段目がピッチ角[rad]のトレンド結果です。
緑で示す出力がピンクで示す目標値に追従していることが分かります。
ただし、制御開始時はSACがまだ推定を開始したばかりの段階であるため、ゲインが収束しておらず、そのために振動的な応答となっています。
続いて2段目がSACの出力であるエレベータ舵角のトレンドです。
多少振動的ではあるものの(実際のアクチュエータはこんなに速く動けないかも?)想定される操作量となっています。
最後の3段目がSAC内部で推定された各ゲインのトレンドです。
見ての通り、目標値が変化を開始してから推定が始まり、およそ10[sec]程で値が収束しています(その後も少し動いていますが)。
なお、一部のゲイン(緑)がかなり大きな値となっていますが、SACはハイゲインな出力フィードバックを構成することによりシステムを安定化すると考えられているため、妥当な動きと言えそうです。
以上から故障の無い理想状態においては、問題なく制御が行えることが分かりました。
SACによるピッチ角制御(故障時)
続いて、故障がある場合の制御を評価してみます。
故障としては、エレベータ舵角に何らかの破損が生じ、通常時の30%しか制御の効果が出せないケースを考えます。
イメージとしてはエレベータ舵角のゲインに総じて0.3が乗じられるような状態です。
故障がある場合のピッチ角の伝達関数モデルを再度線形化によって導出すると以下の通りとなりました。
G_{lon} = \frac{-0.1432s^2-0.07731s-0.0006839}{s^4+0.9511s^3+0.5773s^2+0.005817s+0.003329}
極配置をプロットすると下図となりますが、ノミナル時と比較して固有振動数、減衰性が共に小さくなりました。
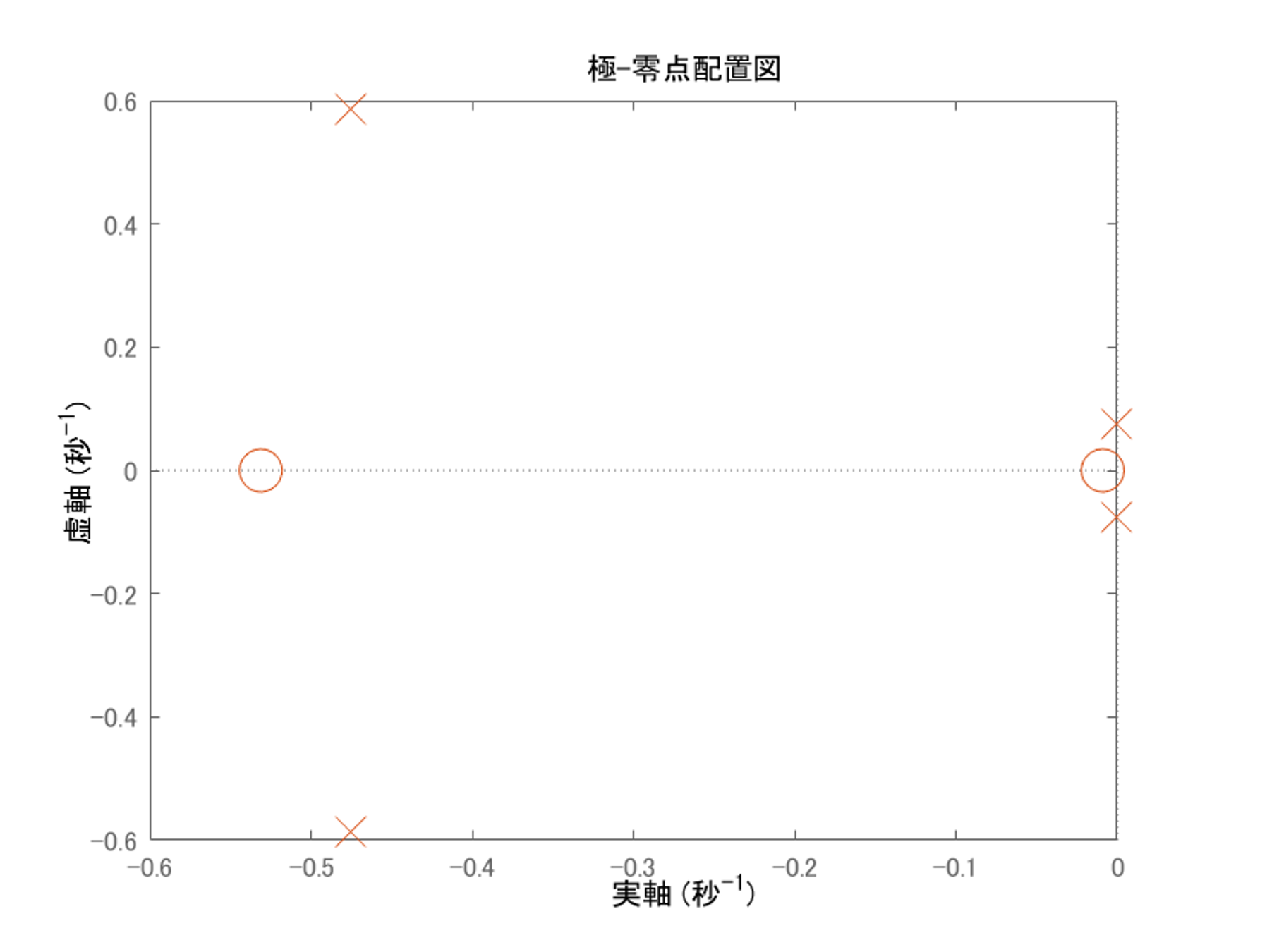
インパルス応答を見てもその傾向は出ています。(軸のスケールをノミナル時のものと合わせています)

エレベータ舵角の制御効果が減少した分、ピッチ角の振幅が小さくなっているのに加え、長周期モードの振動がなかなか収束しません。
この系に対し、ノミナル時と同様のSACを使用して制御性を評価します。
なお、PFCを適用した拡大系は下記の通りとなりますが、故障時でもASPR性は満足しています。
G_{lon_{aug}} = \frac{0.01s^4+01527s^3+0.2262s^2+0.07805s+0.0007172}{s^5+1.951s^4+1.528s^3+0.5831s^2+0.009146s+0.003329}
それでは、故障がある際の閉ループのシミュレーションを確認してみたいと思います。

ノミナル時と比較して、応答は少々劣化しているものの、制御開始時を除いて問題なく目標値に制御している様子が分かります。
ちなみに、比較対象としてPID制御で同様に制御してみた結果(ピッチ角のみ)を以下に掲載します。
なお、PIDのゲインはPID調整器&手動で調整しています。
Kp = 6.0347; % Pゲイン
Ki = 1.9779; % Iゲイン
Kd = 4.5291; % Dゲイン
N = 116.6239; % 疑似微分器フィルター係数

目標値に対しオーバーシュートしているのが分かります。
色々とパラメーター調整を行いましたが、安定性、追従性の両方を追求すると1自由度制御系であるPID制御では難しいようでした。
以上のケーススタディから、SACは適応機構の能力によりプラントの特性が変化しても対処が行えることが分かります。
ただし、推定開始時はゲインがまだ収束していないので正しい制御が行えません。
そのため、予め妥当なゲインの初期値を見積もっておくか、または最初だけ他の安定な補償器で制御して、ある程度時間が経過したらSACに切り替えるといったインターロックを設けることが必要になります。
一方、PID制御のような構造固定化された制御器では、ノミナルと故障時で共通の制御パラメーターを使用して制御するとなかなか性能が出ないケースがあります。
そのため、各動作条件でコントローラーやパラメーターを切り替えて制御するようなゲインスケジューリングの施策が必要になってくる場合があります。
その際、↓の文献のようにロバスト制御の観点で構造固定化された制御器に対するパラメーター設計を検討することが可能です。
Robust Control ToolboxTMによる構造が固定された制御系の解析・設計
以上、一長一短はありますが、適切な施策や制御構成を検討すれば、SACのような適応制御も十分にその真価を発揮できる可能性は十分にあると言えます。
次は、そのような応用例を検討してみたいと思います。
自動着陸問題への適用
先ほどまでは線形なシステムに対する制御で評価を行っていましたが、オリジナルの非線形システムでも制御が可能なのかを確認してみたいと思います。
適用する問題として、先の記事でもトピックとして挙げた自動着陸問題を考え、故障が発生した際の性能評価を行います。
自動着陸の制御システムにおけるSACは、下図で示すようにPID制御で構成される従来制御系に加算するような形での適用を考えます。

SACをPID制御と併用することで推定開始時の問題に対処する他、もしSACに異常があれば純粋なPID制御に戻すことが可能です。
なお、SAC適用に伴い、連続時間系で作ったSACのモデルを制御周期10[ms]で離散化します。
モデルを離散化する際は、↓のようにControl System Toolboxの機能を利用すると比較的スムーズにできます。
SACのパラメーターは以下のように再調整します。
Tm = 2; % 規範モデルの時定数(規範モデルは1次遅れ)
gamma_I = 100*eye(3); % 積分調整則のゲイン
sigma_I = 0.0001; % シグマ調整項
c0 = zeros(1,3); % 積分器の初期値
それでは、シミュレーションによってエレベータ故障時(制御効果が30%に低下)のFTC(SAC)有無によるパフォーマンスの比較を行います。
なお、環境からの外乱として突風外乱(Dryden model)を考慮します。
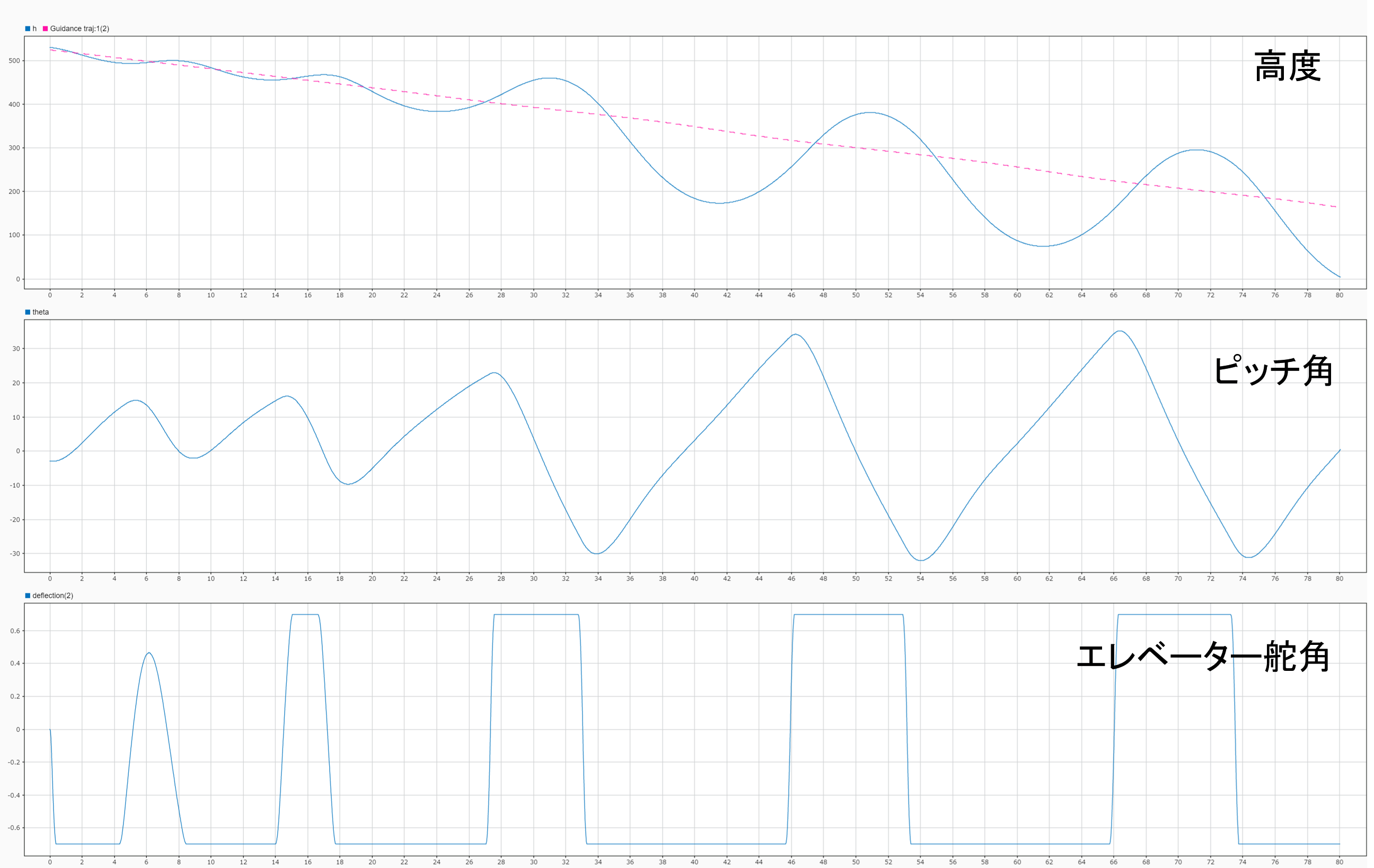
結果を見ると分かるようにFTCが無い系は、制御が発散し、最終的には機体が墜落してしまいます。
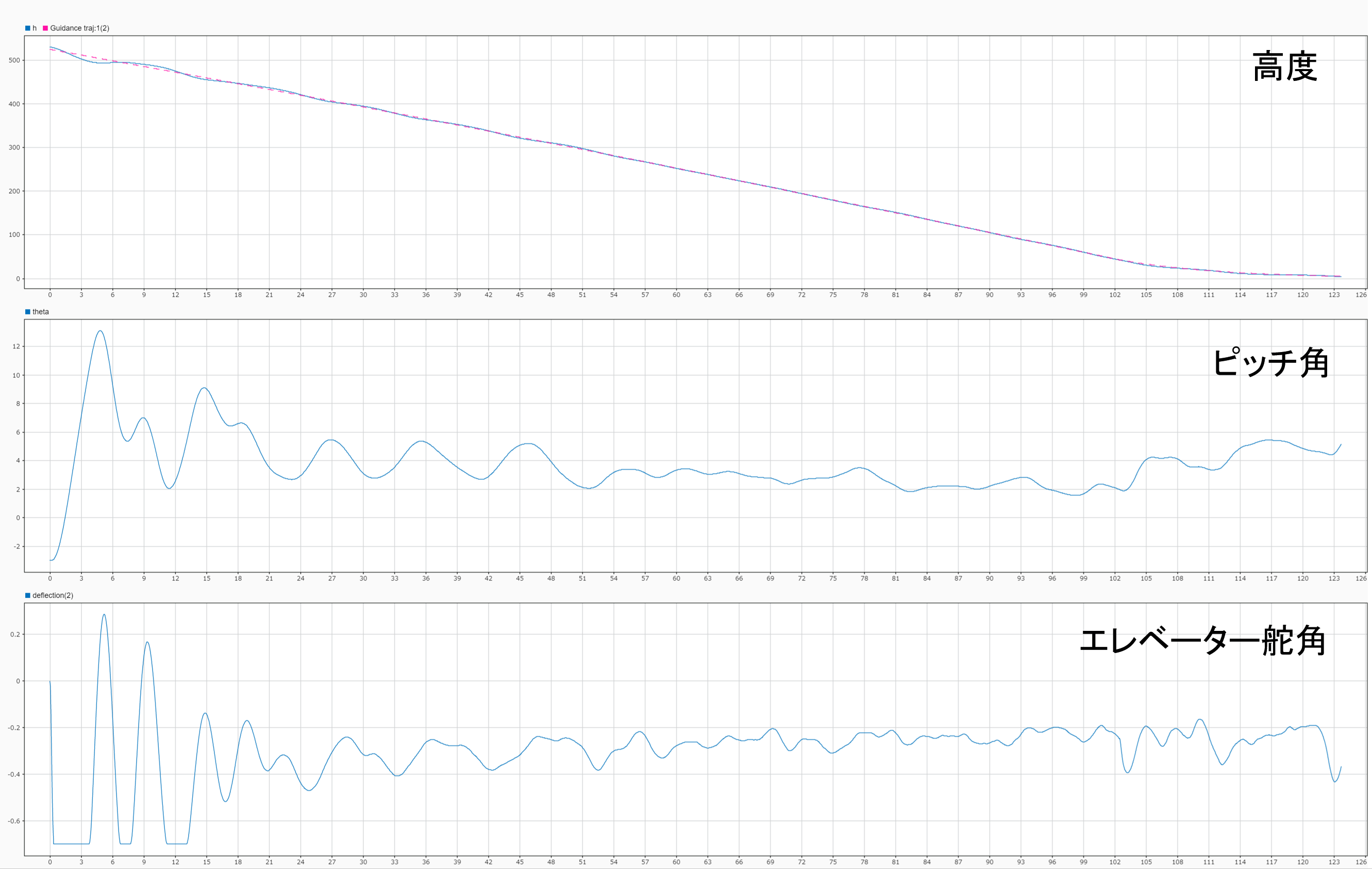
FTCがある系は、故障時においても制御が発散することなく、ランディングすることに成功しています。
以下はそれぞれの飛行アニメーション(n倍速で送っています)です。
FTCが無い場合は、機体が常に大きくピッチングしています。
一方、FTCがある場合は、故障しているとは思えないくらい滑らかに制御されています。
このようにSACによるFTCは故障時に対するロバスト性を一定程度高める効果があることが分かります。
最後に
今回は航空機の耐故障制御を題材に適応制御の一種であるSACを用いてその性能を確認してみました。
故障を補償する仕組みは非常に重要であるとともに、システムとしての安全性や信頼性をどのように保証するかという難しさもはらむ内容です。(認証系など)
ちなみに適応制御理論は一時期盛んに研究されていましたが、ブラックボックスかつパラメーター調整が難しいために、制御を知らない現場の人間からすると得体の知れない制御として捉えられることが多く、結局は信頼性がないということでなかなか産業界に浸透できなかったように思います。
SACのような単純な構造の制御であれば、適用しやすいかもしれませんね。
参考文献
[1] 大森優也、鈴木真二、増位和也 著:MuPAL-αでの単純適応制御による耐故障飛行制御システムの飛行実証、第51回飛行機シンポジウム講演集
[2] 岩井善太、水本郁朗、大塚弘文 著:単純適応制御 SAC、 森北出版