こんにちは,株式会社Nospareリサーチャー・千葉大学の小林です.
今回はJournal of Royal Statistical Society Series Aにも掲載されたGabry et al. (2017)(arXiv版)の紹介をします.この論文では次の挙げられるベイズ分析のワークフロー
- 探索的データ分析
- 分析前のモデルチェック
- アルゴリズムの動作チェック
- モデル推定後のモデルチェック
において視覚化をどのように使っていくかについて書かれており,実証分析や実務においてベイズ分析を行うにあたってとても有用な内容になっています.本記事で掲載する図などは著者がgithubにポストしてあるコードを使って作成しました.
データ分析例の設定
この論文では終始PM2.5に関するデータ分析例を取り扱っており,この例では以下の設定があります.
- PM2.5は人体に対して影響があると考えられ,本当は健康上のアウトカムとの関係を調べたい
- 世界中のいろいろな都市で(2980地点)でPM2.5の地表濃度が観測・集計されているが(下地図の+),観測地点はスパースで,空間上で偏りがある(アフリカ,アジア,ロシアで少ない)
- 衛星からのPM2.5の濃度の推定値のデータがある(下地図の色)ので,必要な地点におけるPM2.5の濃度を予測したい
- 適切な予測モデルの構築を行う

探索的データ分析
まず分析のためのモデルを書いたりする前に,探索的分析(exploratory data analysis)を行いますが,これはただサマリーをプロットしてレポートするだけというよりかは,データに内在する特徴や異質性を捉えるための複雑なモデルのネットワーク(network of models)を構築するのに重要なステップであるとしています.このPM2.5の例のようにデータがスパースだったりアンバランスだったりする場合には,こういった制約のもとでモデルのネットワークを構築することができます.機械学習でよくある,手持ちのデータをとりあえず複雑なノンパラメトリック手法に突っ込んで処理するというようなアプローチは,データが関心のある母集団をよく表している場合にはうまくいきますが,このPM2.5のデータでは北アメリカやヨーロッパの情報がほとんどなので,予測モデルが示唆する汚染のプロファイルは開発国のものとは全然異なってしまう可能性があります.
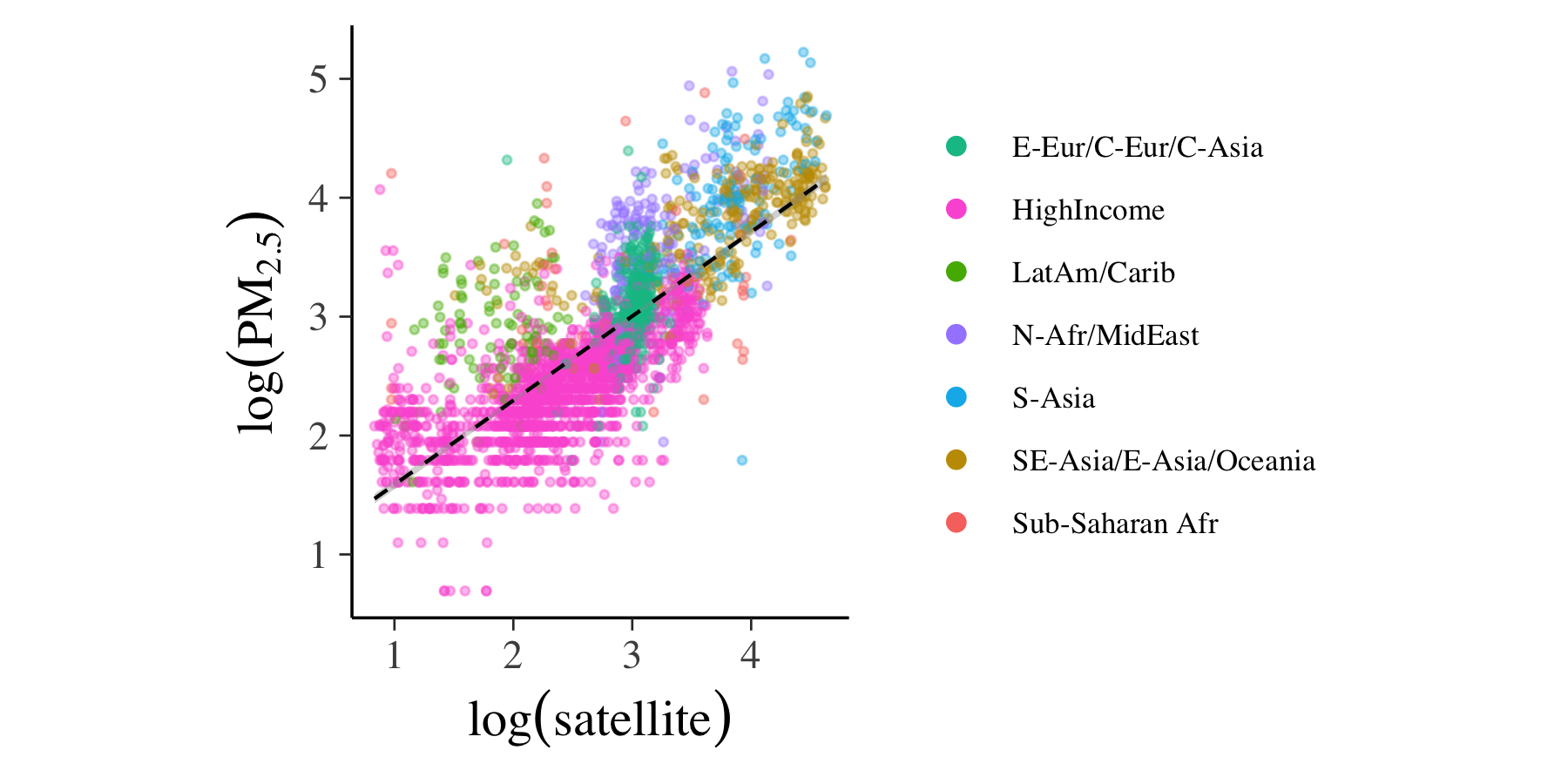
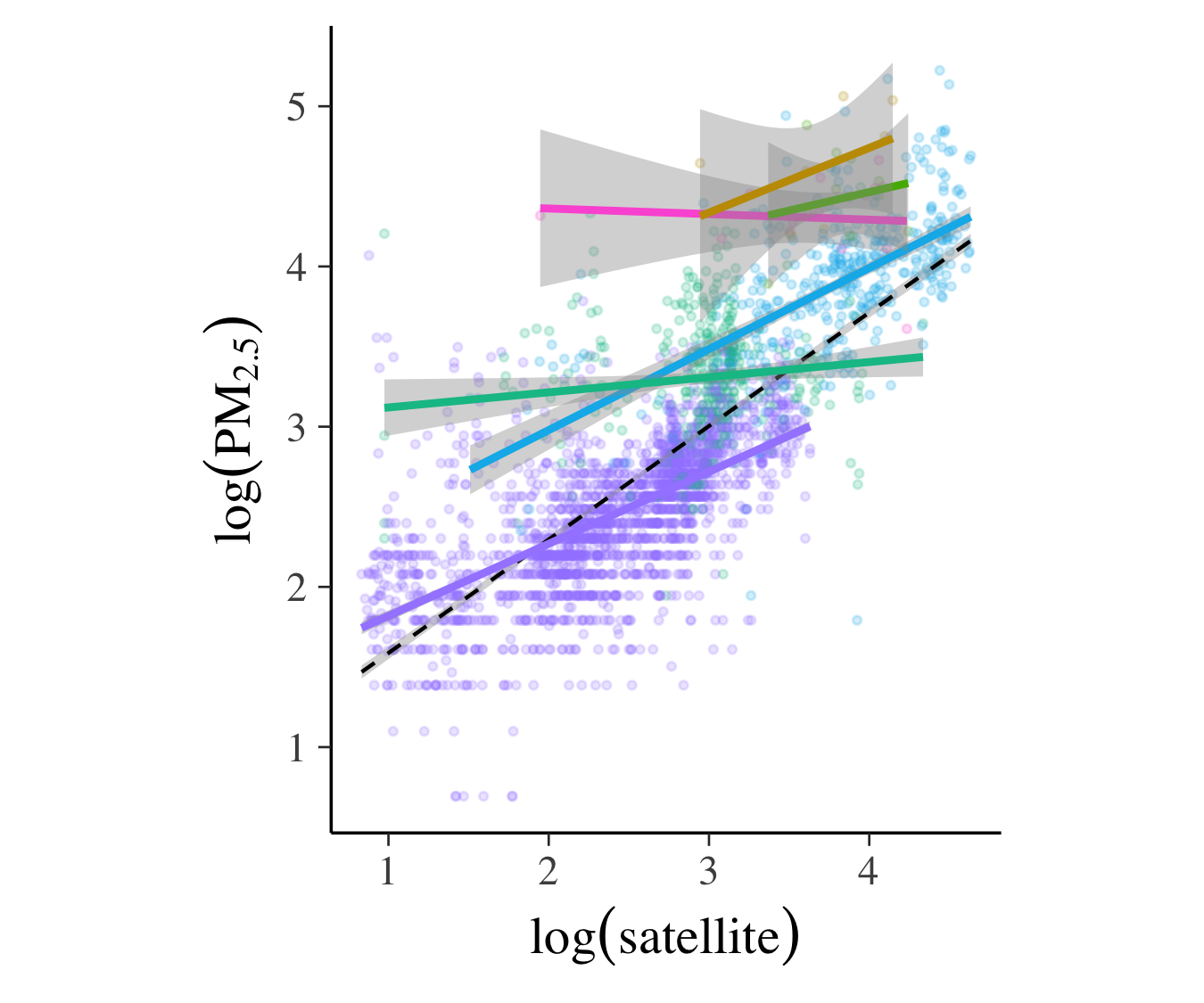
まず一番単純な予測モデルとして,地表濃度の対数を衛星からの推定値の対数に回帰させることが考えられます.下の図のように,それなりに線形の関係があることが見れます($R^2\approx 0.6$).
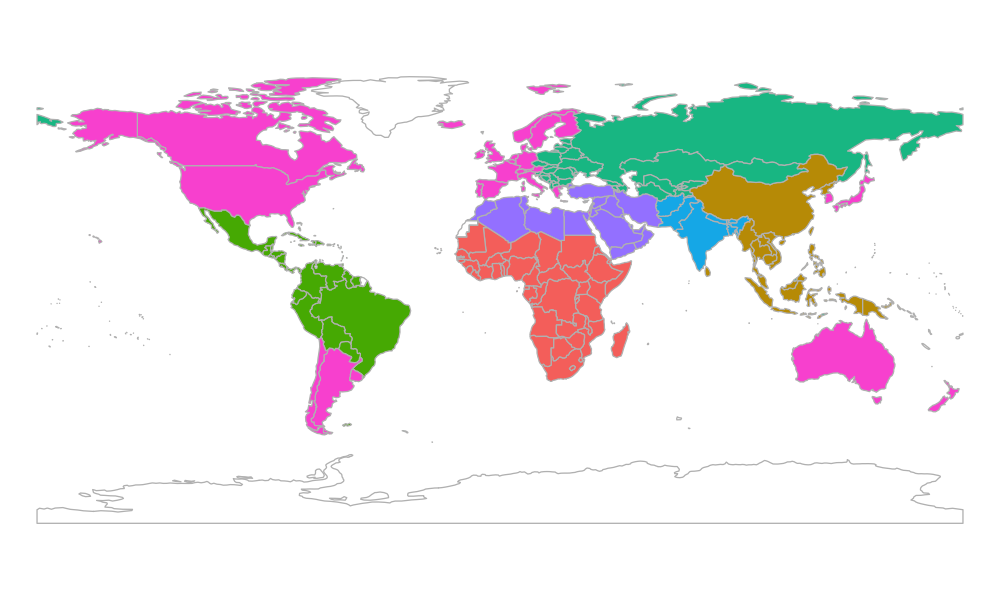
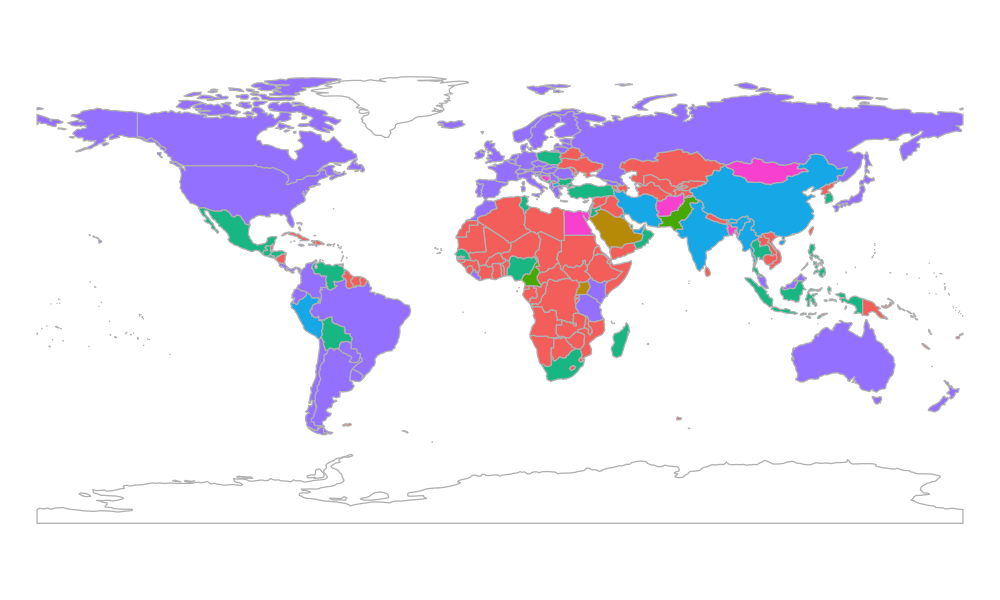
よりモデルを改善させるために,国ごとの異質性を考慮してみます.たとえば大気汚染の度合いは工業化の進み具合によって先進国と開発国とでは異なるし,砂漠の砂がPM2.5の原因のひとつであることも知られています.ここでは各国のグルーピングの仕方について次の2通りを考えます.
- 先進国(WHO基準)とその他の各地域(左図)
- 地表濃度を階層クラスタリングしたもの
 |
 |
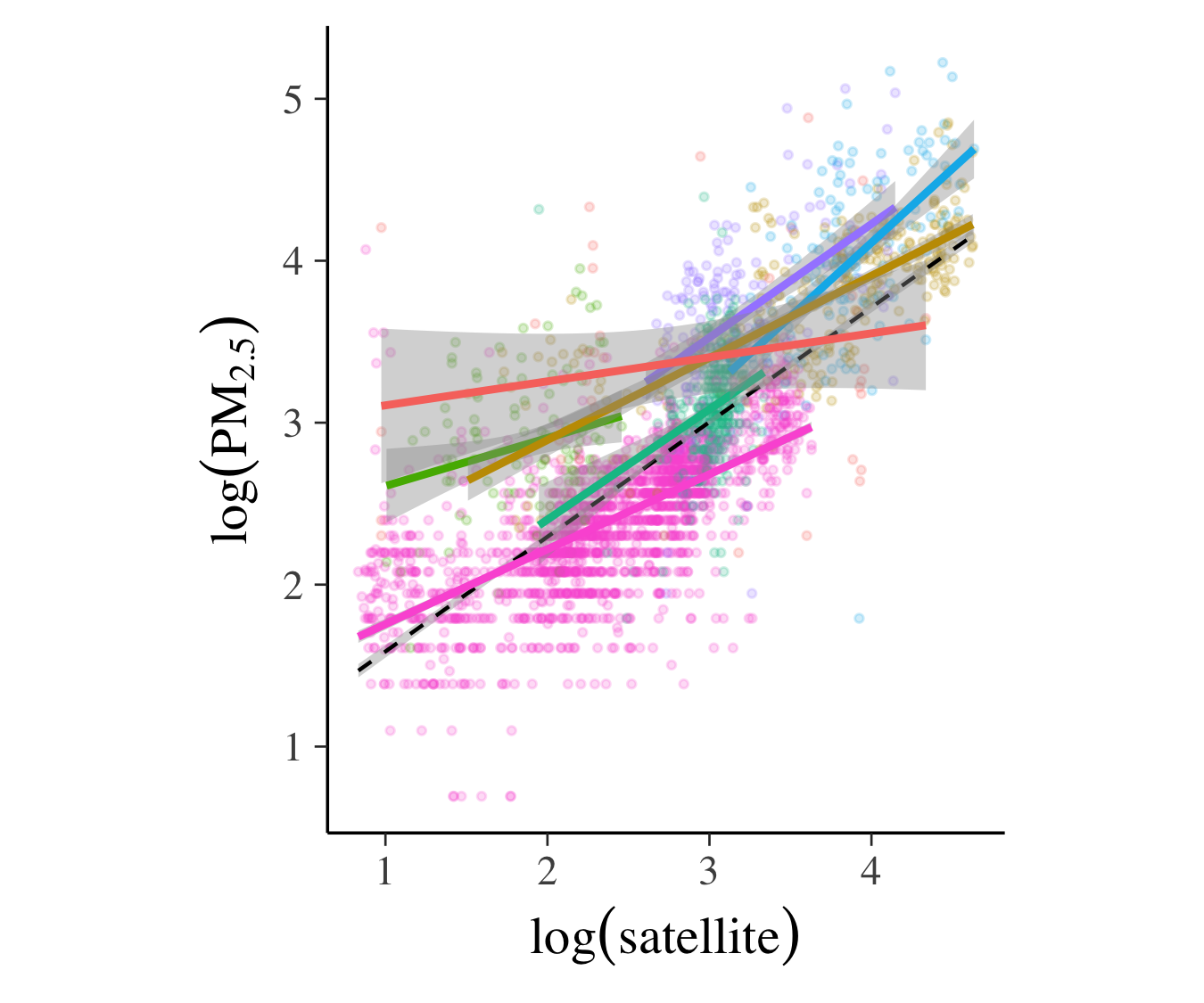
以下の図は各グループごとに回帰モデルを当てはめた結果ですが,グループによってかなり異質性があることが見て取れ,単純な回帰モデル一本だけではデータの特徴を捉えるには不十分であると言えます.
 |
 |
これらの探索的データ分析から,次の3つのモデルがモデルのネットワークの中に浮かび上がってきました.
- モデル1:単回帰モデル
- モデル2:WHO基準に基づいてグループ化したマルチレベルモデル
- モデル3:地表濃度のクラスターに基づいてグループ化したマルチレベルモデル
分析前のモデルチェック
これらの3つのモデルのパラメータについて正則事前分布(proper prior)を仮定することで,ベイズモデルから事前予測分布(prior predictive/marginal distribution)を得ることができます.この事前予測分布をチェックすることで事前分布の設定が所与の問題においてどのように働くかを評価することができます.具体的には,事前予測分布が観測されたデータと近いところに位置しているかを見ます.
上記のマルチレベルモデルは次のように書けます.
y_{ij}\sim N(\beta_0+\beta_{0j}+(\beta_1+\beta_{1j}x_{ij},\sigma^2), \quad \beta_{0j}\sim N(0,\tau^2_0),\quad \beta_{1j}\sim N(0,\tau_1^2)
ここで$j$がグループ,$i$がグループ内の国のインデックス,$y_{ij}$と$x_{ij}$はそれぞれ対数地表濃度と衛星からの推定値の対数です.
まずパラメータの事前分布として次の設定を考えます.
- まずよくありがちな設定で,$\beta_k\sim N(0,100)$,$\tau_k^2\sim IG(1,100)$.
- 衛星からの推定値がPM2.5の濃度をちゃんと反映していると仮定:$\beta_0\sim N(0,1)$, $\beta_1\sim N(1,1)$, $\tau_k\sim N^+(0,1)$($N^+$は半正規分布を表す)
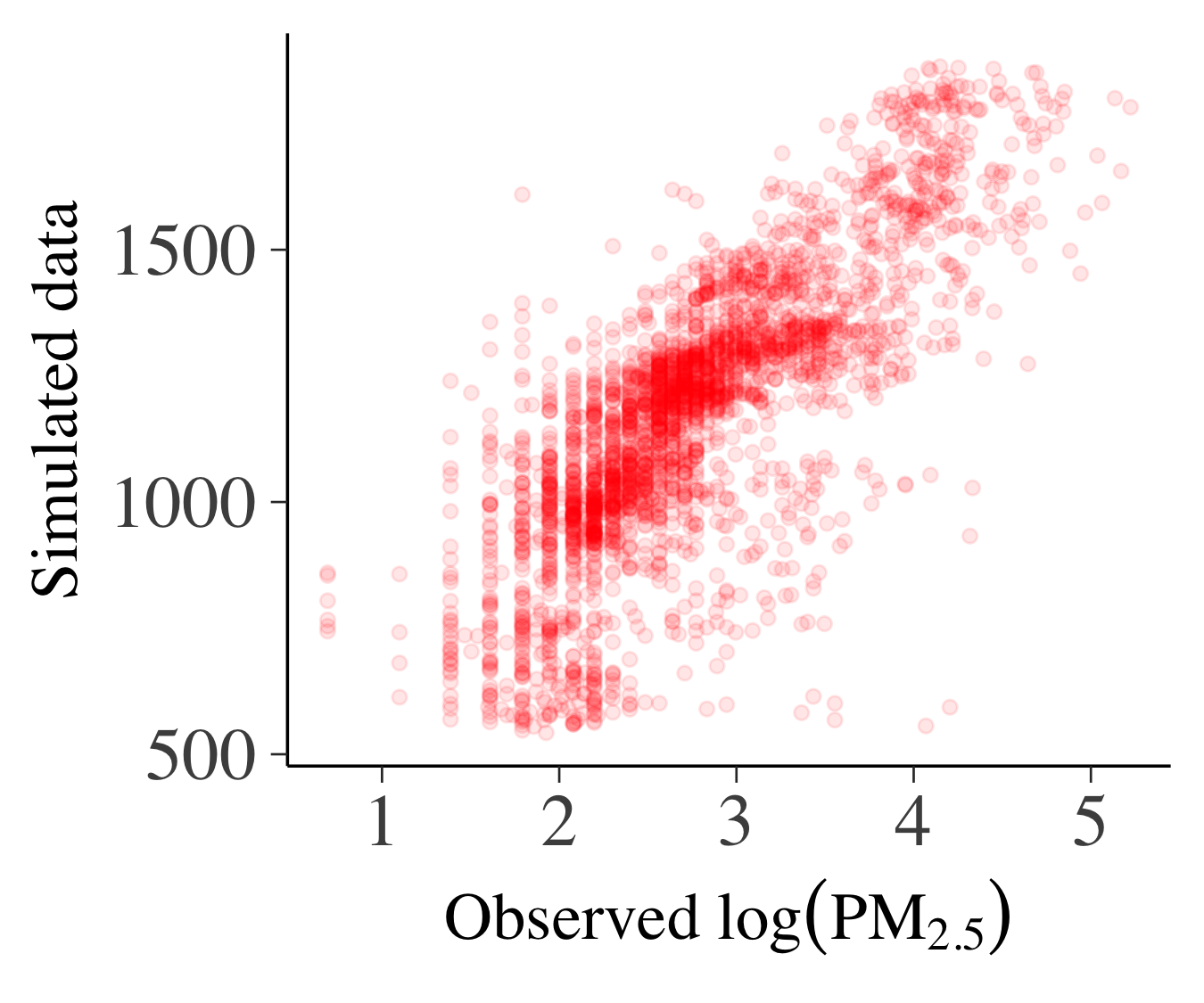
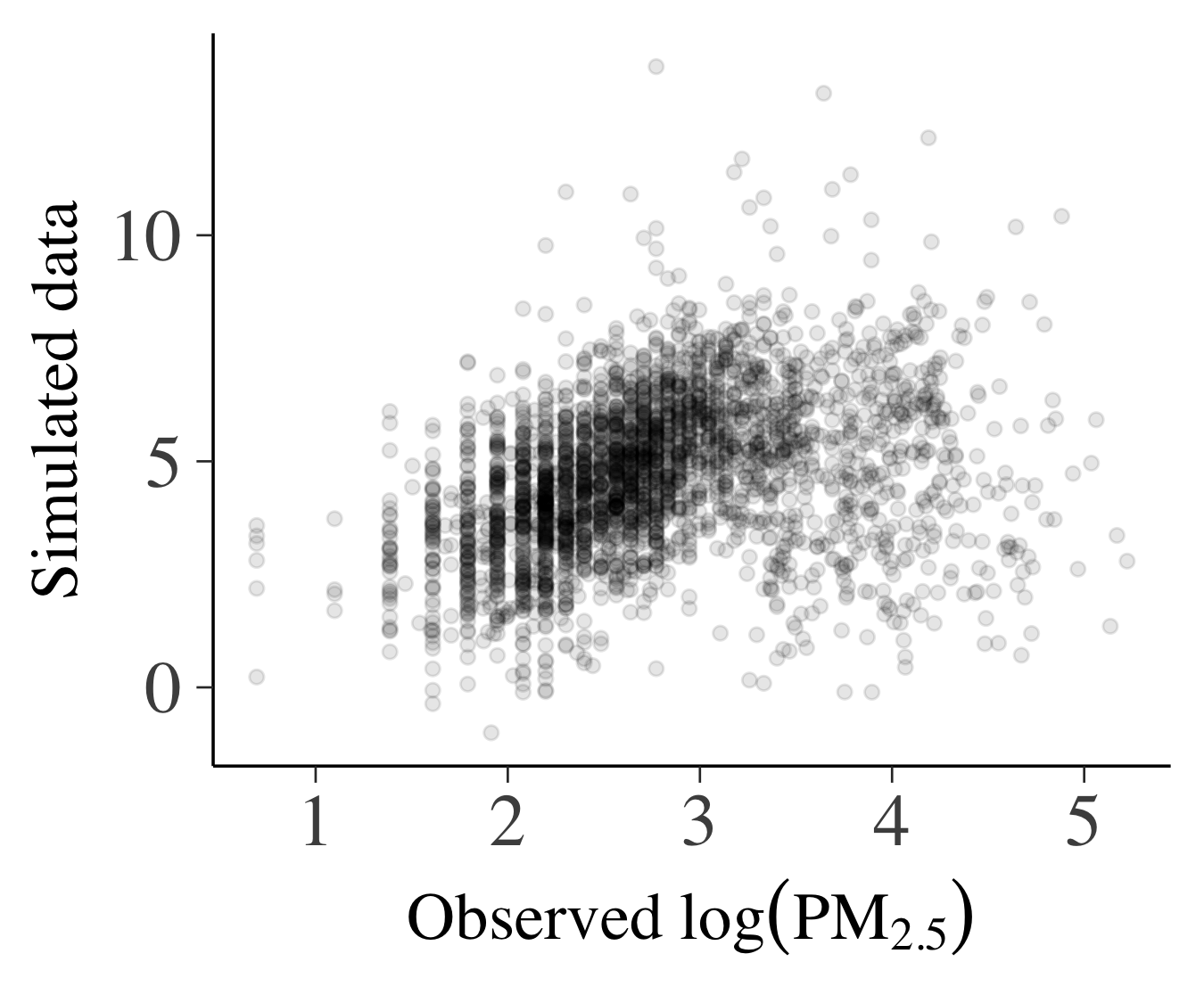
これらの事前分布からパラメータの値を生成し,回帰モデルからデータを生成します.下の図は事前予測分布からの実現値と観測されたデータの比較になります(左:設定1,右:設定2).軸の目盛りをみると,設定1での事前予測分布からの実現値は実際のデータとまったく異なる領域に分布していることがわかります.一方で設定2では実際のデータと同じような領域に分布しており(事前予測分布のほうが広がりは大きいですが),こちらのほうがより適切であると考えられます.
 |
 |
アルゴリズムの動作チェック
いよいよモデルを推定しますが,ここでも視覚化は重要です.
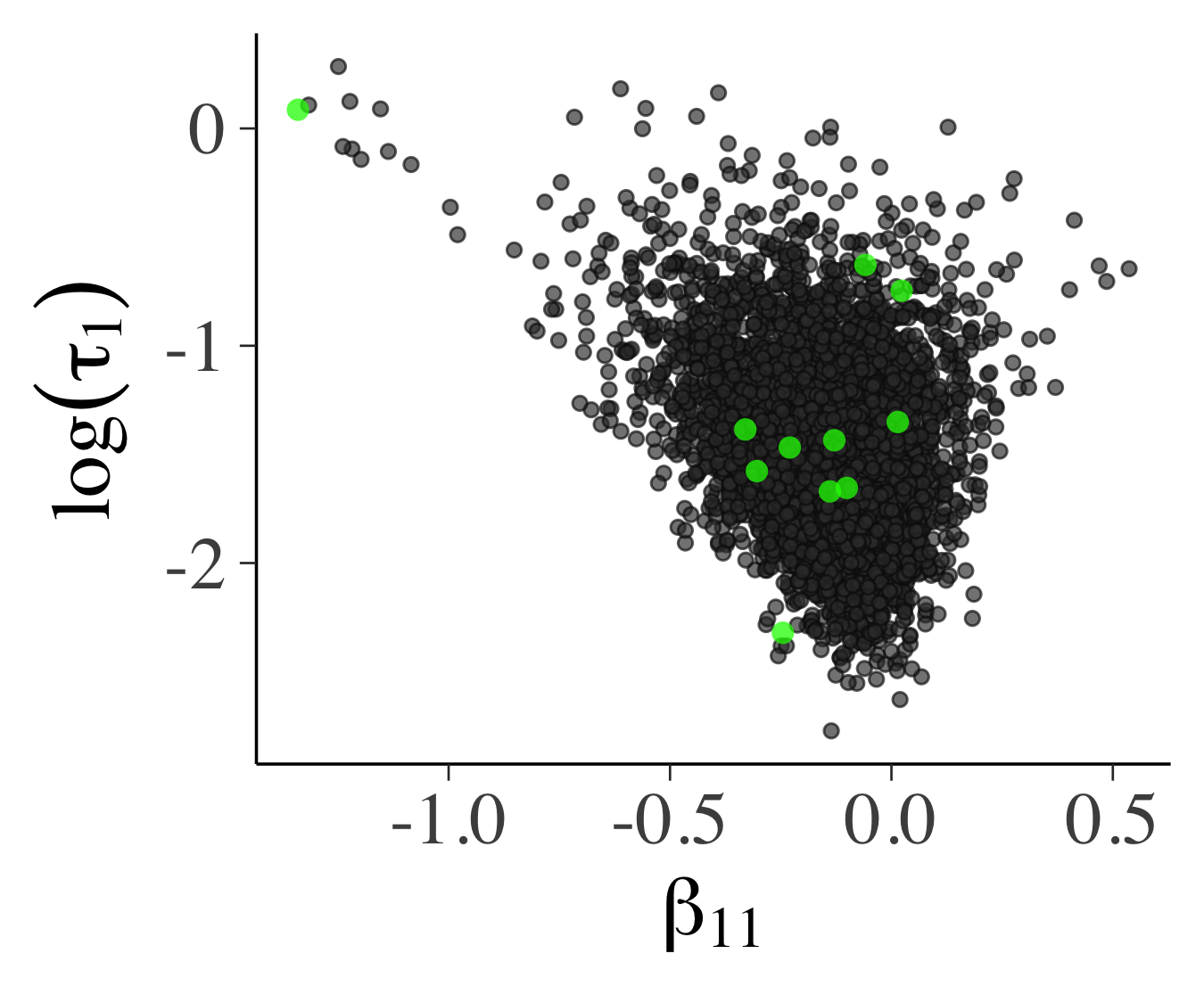
本分析で利用するハミルトニアンモンテカルロ法(HMC)においては,事後分布のジオメトリーを利用しますが,ジオメトリーがなめらかでない場合にはリープフロッグを使ったHMCの軌跡は,総エネルギーを維持するような軌跡から発散することがあります.このような軌跡を検知するには,ハミルトニアンの誤差がある大きな閾値を超えたときに発散したとフラグを立てます.誤ってフラグを立てた場合でも,サンプルが発散しなかった場合のサンプルと比較して同じように分布していれば,フラグを取り消すことができます.軌跡が発散するのは,上記のように事後分布の問題のある(事後分布の曲率が大きい)領域に集中しやすいので,サンプルの視覚化を行うことでMCMCの収束や事後分布のジオメトリーのチェックを行うことができます.
以下の図は$\beta_{11}$と$\log(\tau_1)$のプロット(左)と各パラメータのパラレルコーディネート(右)です.図において緑色の点または線は発散する遷移を表しています.左図で,緑色の点の分布に関してあまりこれといったパターンが見られないので,これらのほとんどは誤検知であると考えられます.
 |
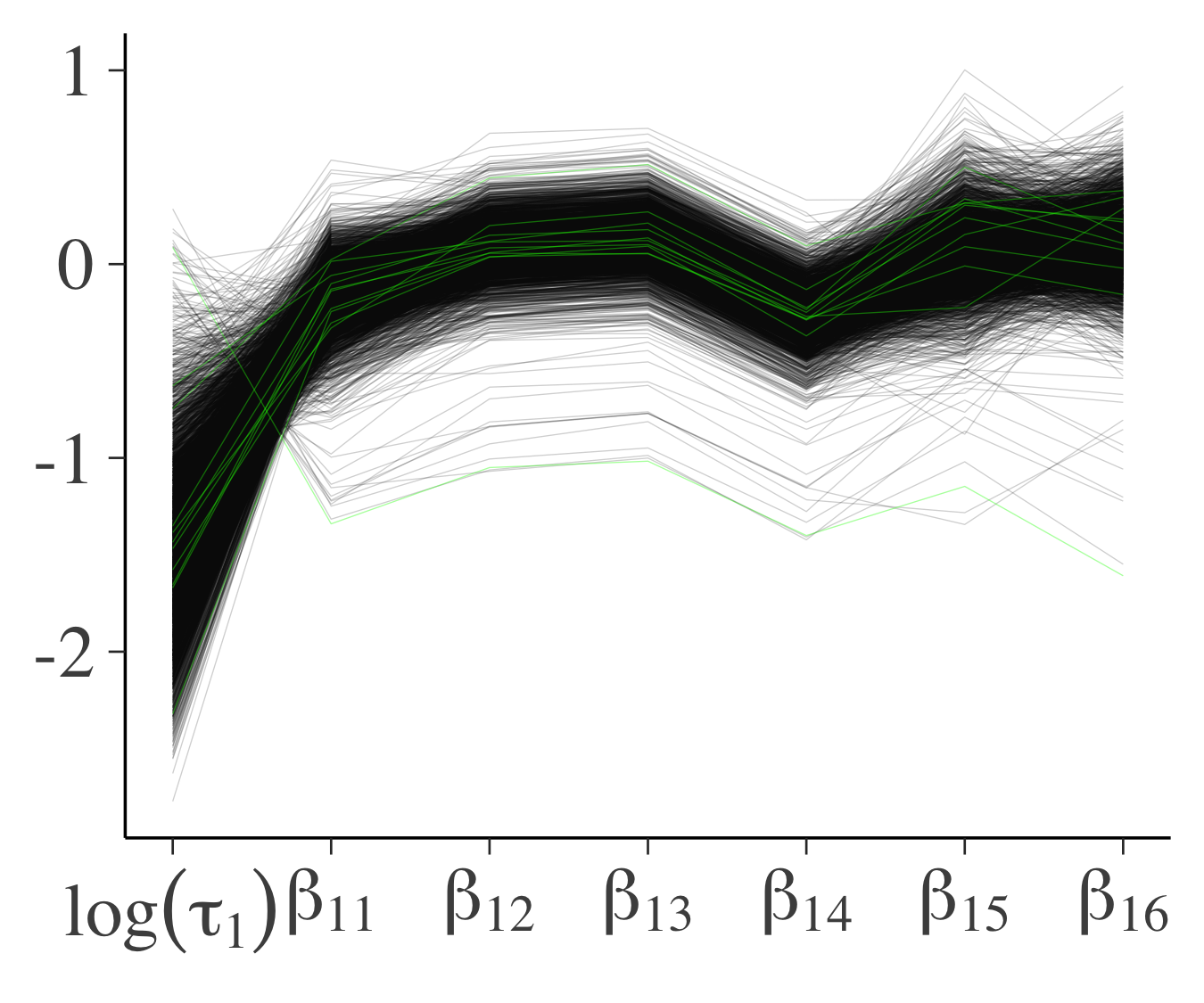 |
一方でこの論文の付録では,発散する遷移の分布に明確なパターンがある場合(別のデータ,モデル)についても言及していて,そこでは下図左の下側の領域が事後分布において問題のある領域であることが見れます.下右図を見ると,$\tau$というパラメータが小さいときに問題のある遷移が起こるということが明確にわかります.
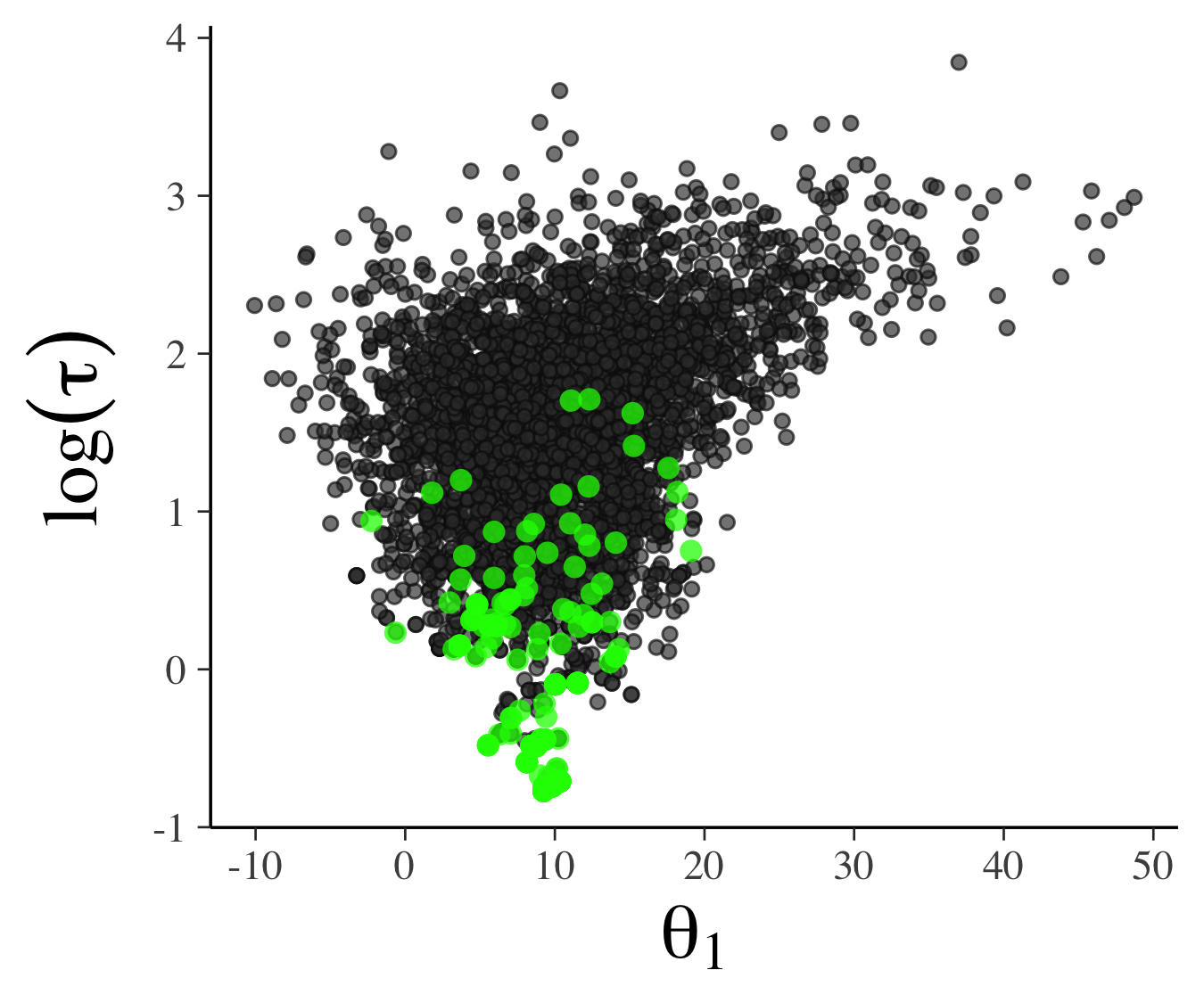 |
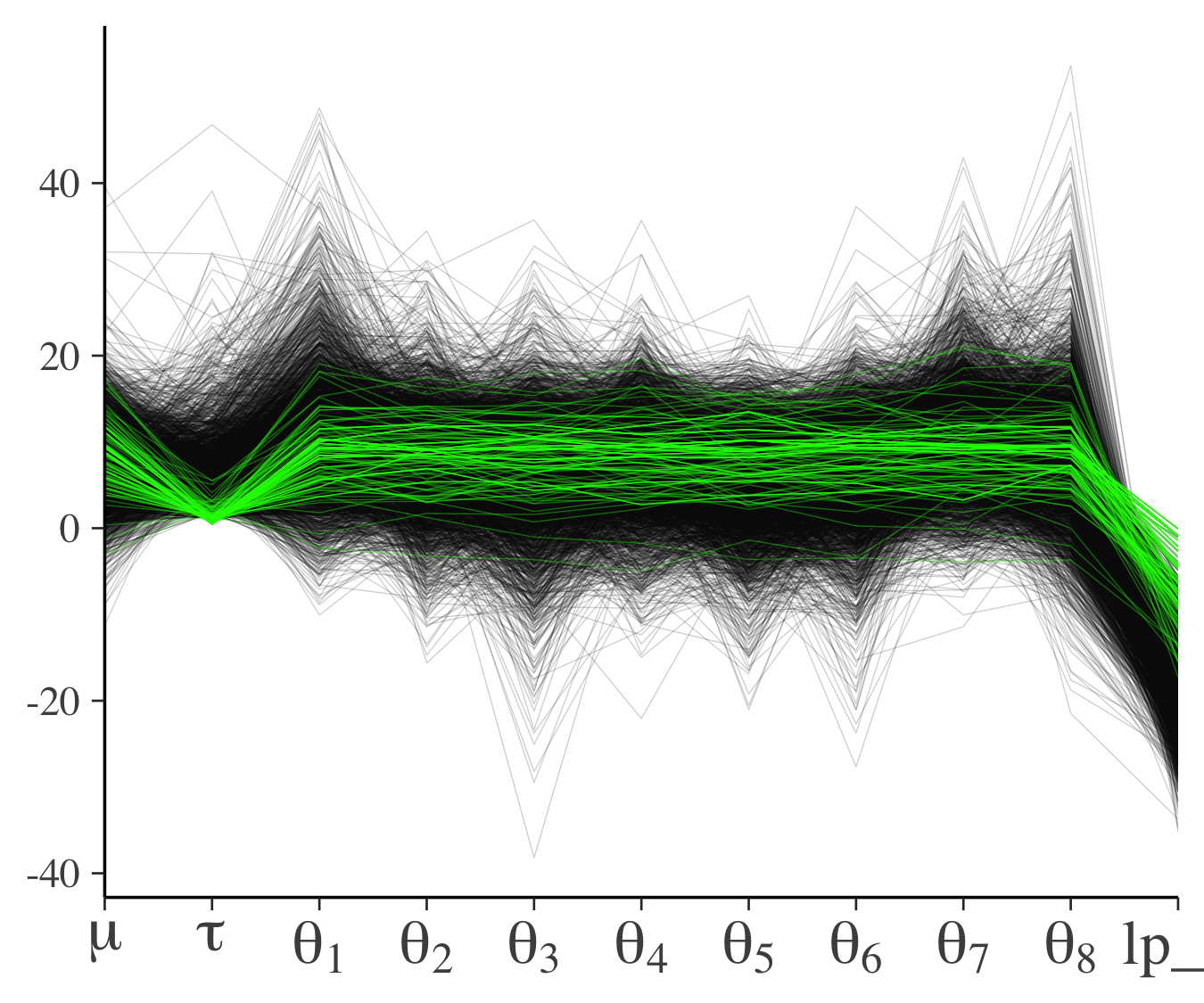 |
モデル推定後のモデルチェック
事後予測分布
モデル推定後に使用したモデルがどれほどうまくあてはまっているかを事後予測分布(posterior predictive distribution)に基づいて行います.ここでの操作は事前予測分布のときと似ていますが,パラメータの値は事後分布から生成したものを使います.モデルのあてはまりがよければ観測されたデータと同じような予測値を生成することができます.
PM2.5についての3つのモデルの比較を事後予測分布に基づいて行います.下図は観測データのカーネル密度推定値(実線)と事後予測分布からの100個のシミュレーション(薄い色)になります.図では一番左のモデル1(単回帰モデル)は事後予測分布が実際のデータから離れたものになっているのに対し,ふたつのマルチレベルモデルでは事後予測分布と観測データは似ています.
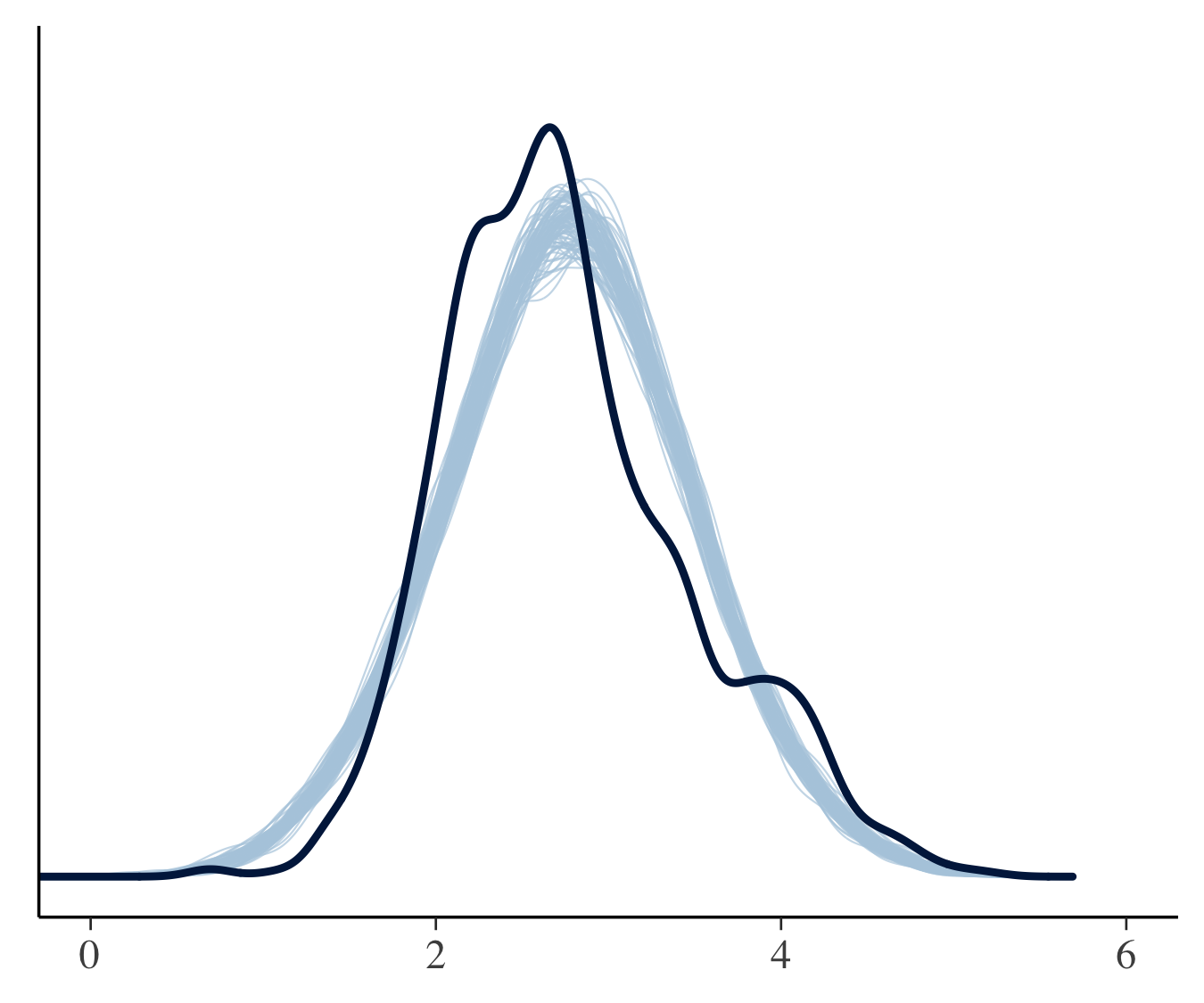 モデル1 モデル1 |
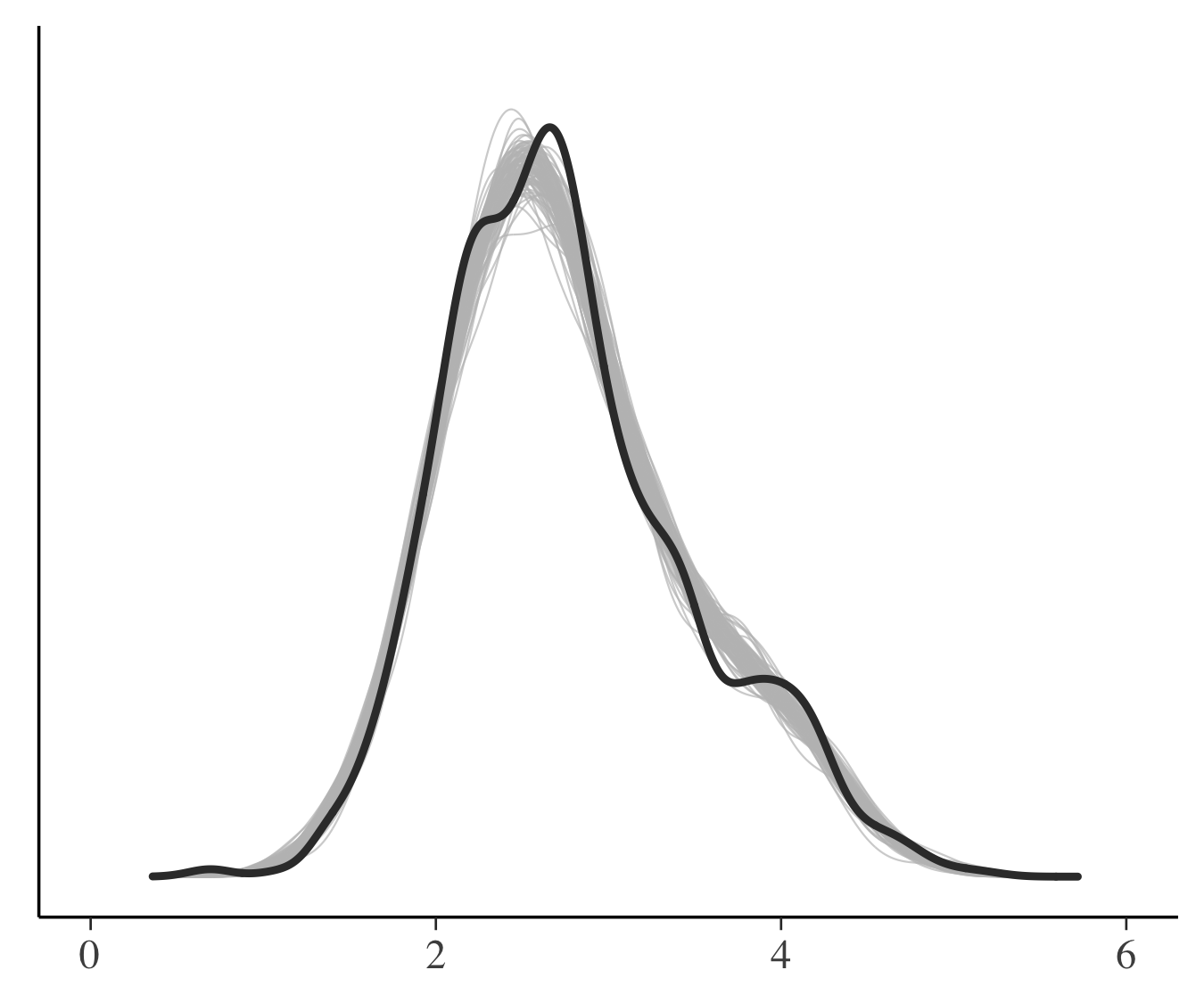 モデル2 モデル2 |
 モデル3 モデル3 |
ここで行った事後予測分布に基づいたチェックは推定と予測のバリデーションにデータを2回使ってしまっています.なのでこの代わりにパラメータと直行するような統計量に関してチェックを行います(パラメータと関係するような統計量を選んでしまうと,データと予測のコンフリクトを検知しにくくなります).ここでは,事後予測分布が歪度をどれだけうまく捉えられているかをチェックします.下図の垂直な線は観測されたデータの歪度を表しており,各パネルは事後予測分布のシミュレーションから計算した歪度のヒストグラムを表しています.上の事後予測分布のチェックでは2つのマルチレベルモデルは同じような結果でしたが,歪度に関するチェックを行ってみるとモデル3のほうがよく歪度を捉えていることがわかりました.
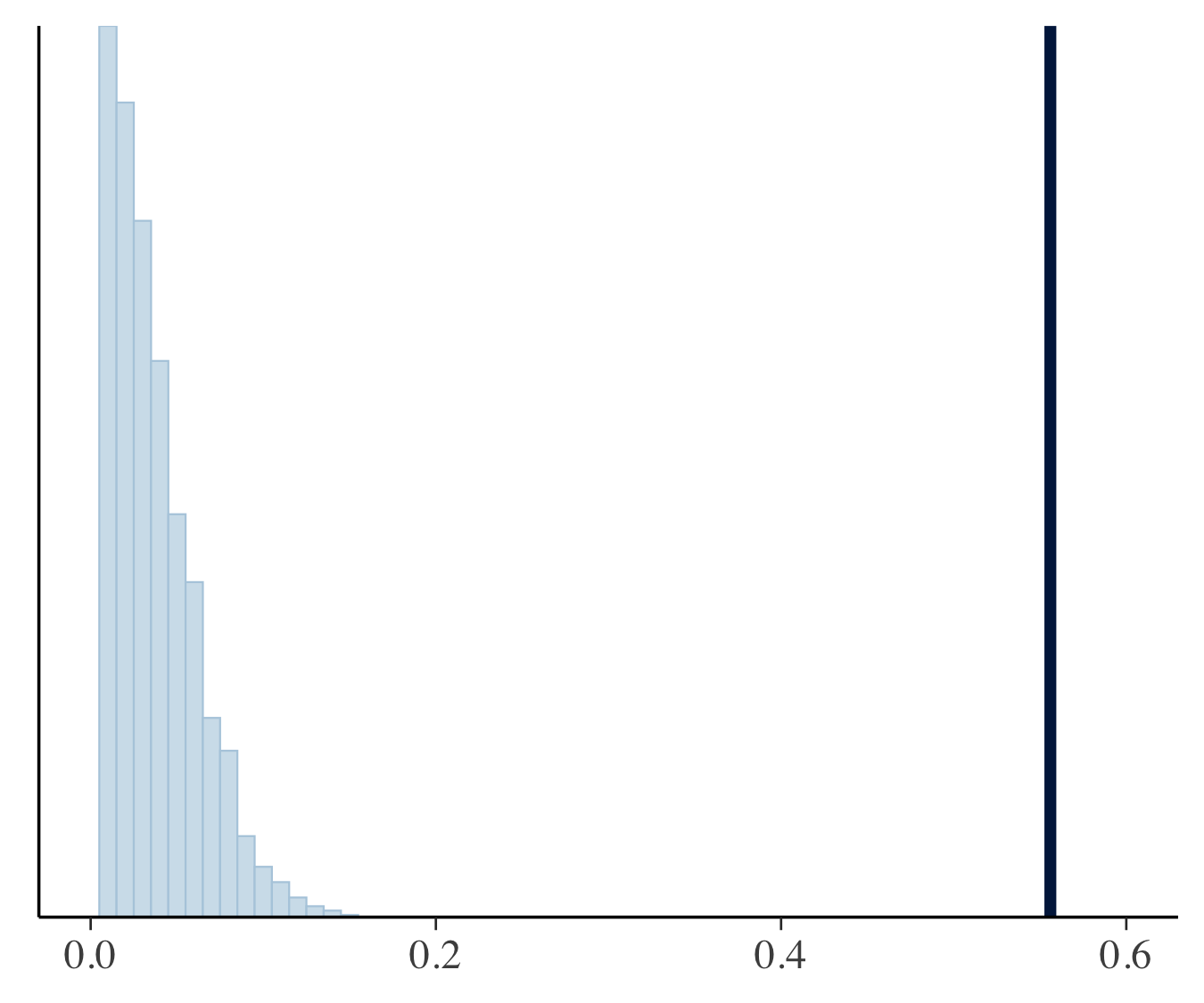 モデル1 モデル1 |
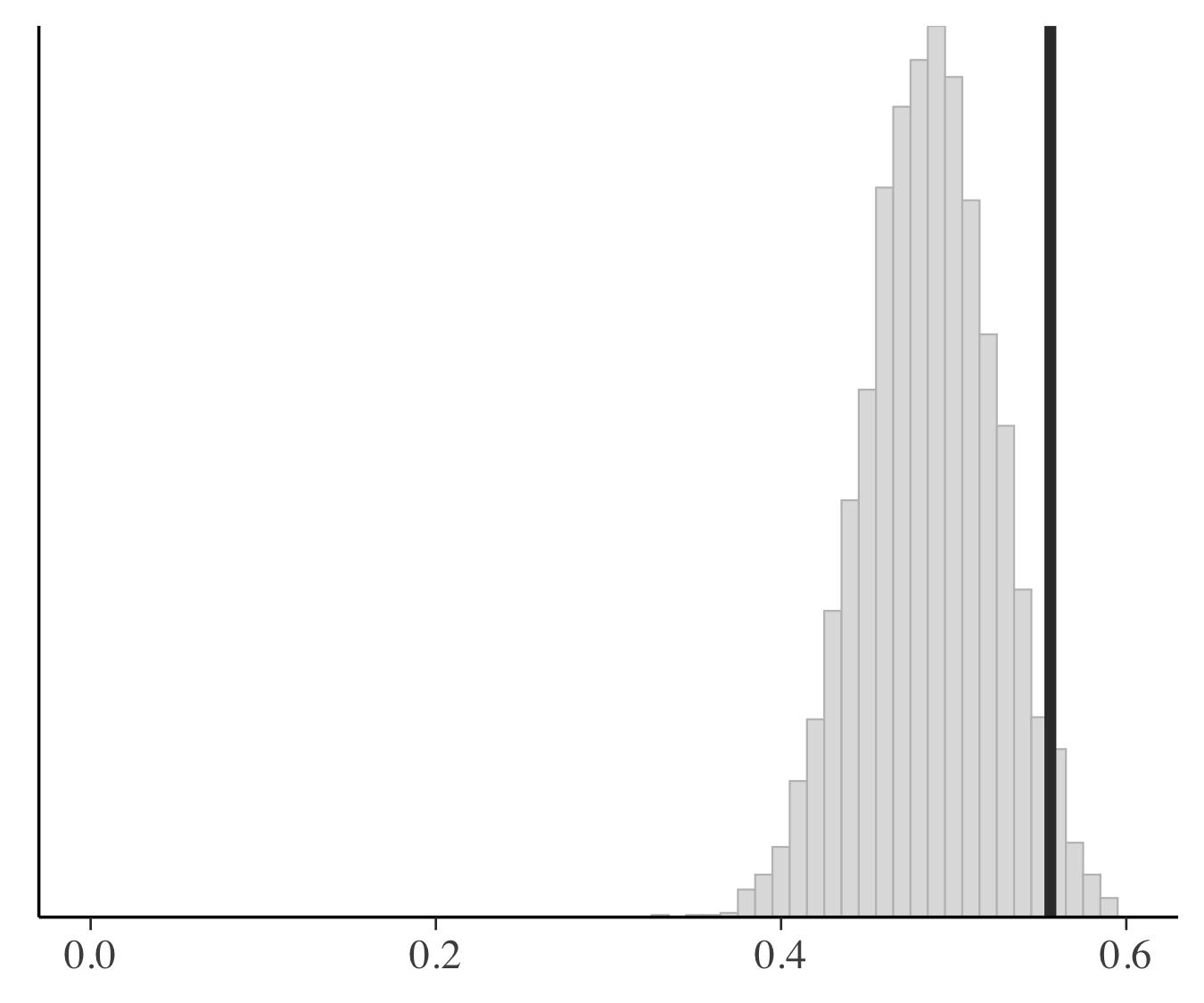 モデル2 モデル2 |
 モデル3 モデル3 |
一個抜き交差検証(LOOCV)によってデータを2回使うのを部分的に回避することができます.カリブレートされたモデルにおいてはLOOCVの予測累積分布関数が漸近的に一様分布になるので,一様分布に近くなっているモデルがよいことになります.下図は細い線が一様分布からのシミュレーションで,太い実線がLOOCVののprobability integral transformになります.モデル1は一様分布から大きく逸脱していますが,2つのマルチレベルモデルはモデル1からの改善が見られます.マルチレベルモデルでは0.5あたりで山なりになってなっており,予測分布が観測データよりも広くなっていることを意味しています.マルチレベルモデルに関してもまだまだ改善の余地がありそうです.
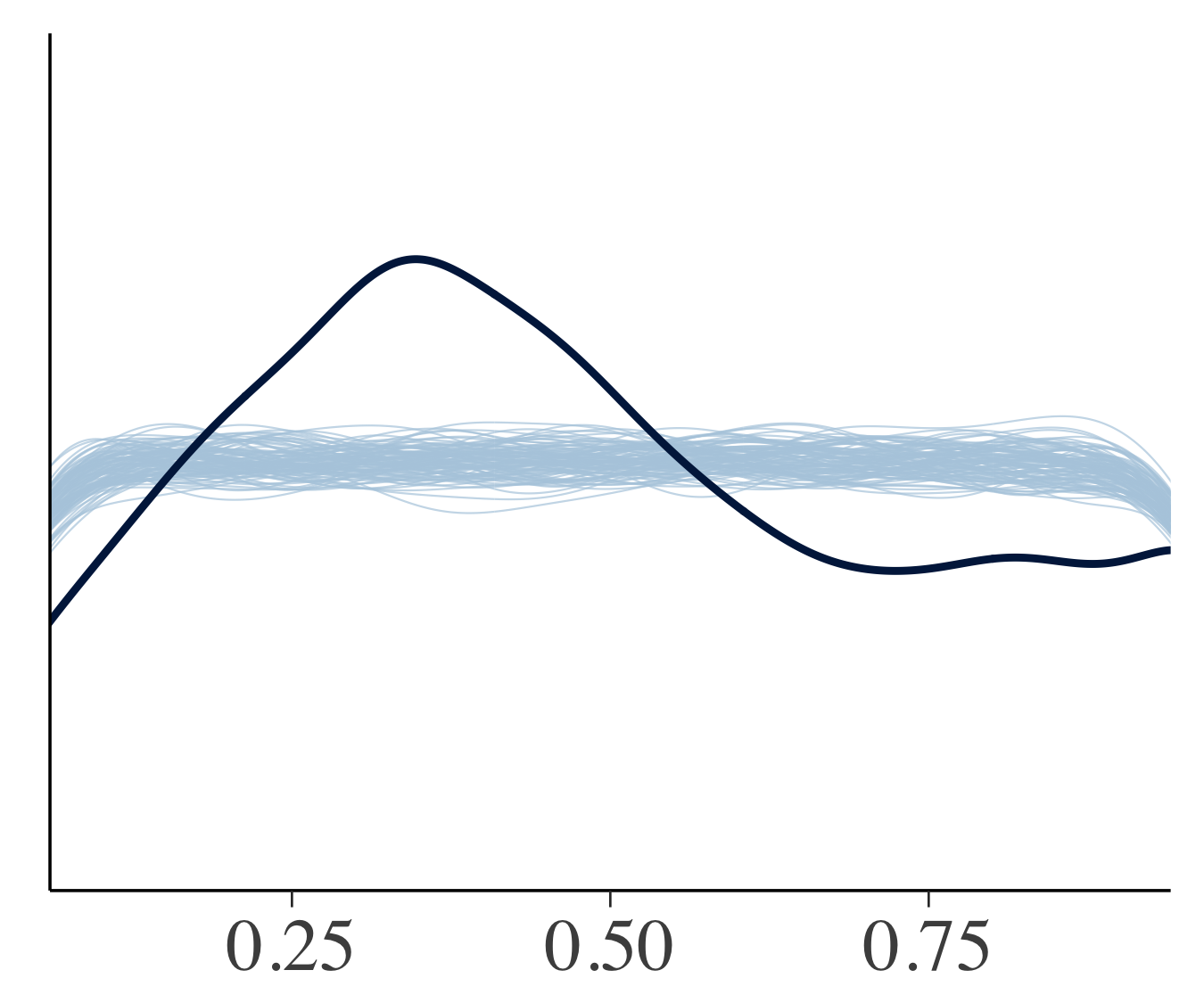 モデル1 モデル1 |
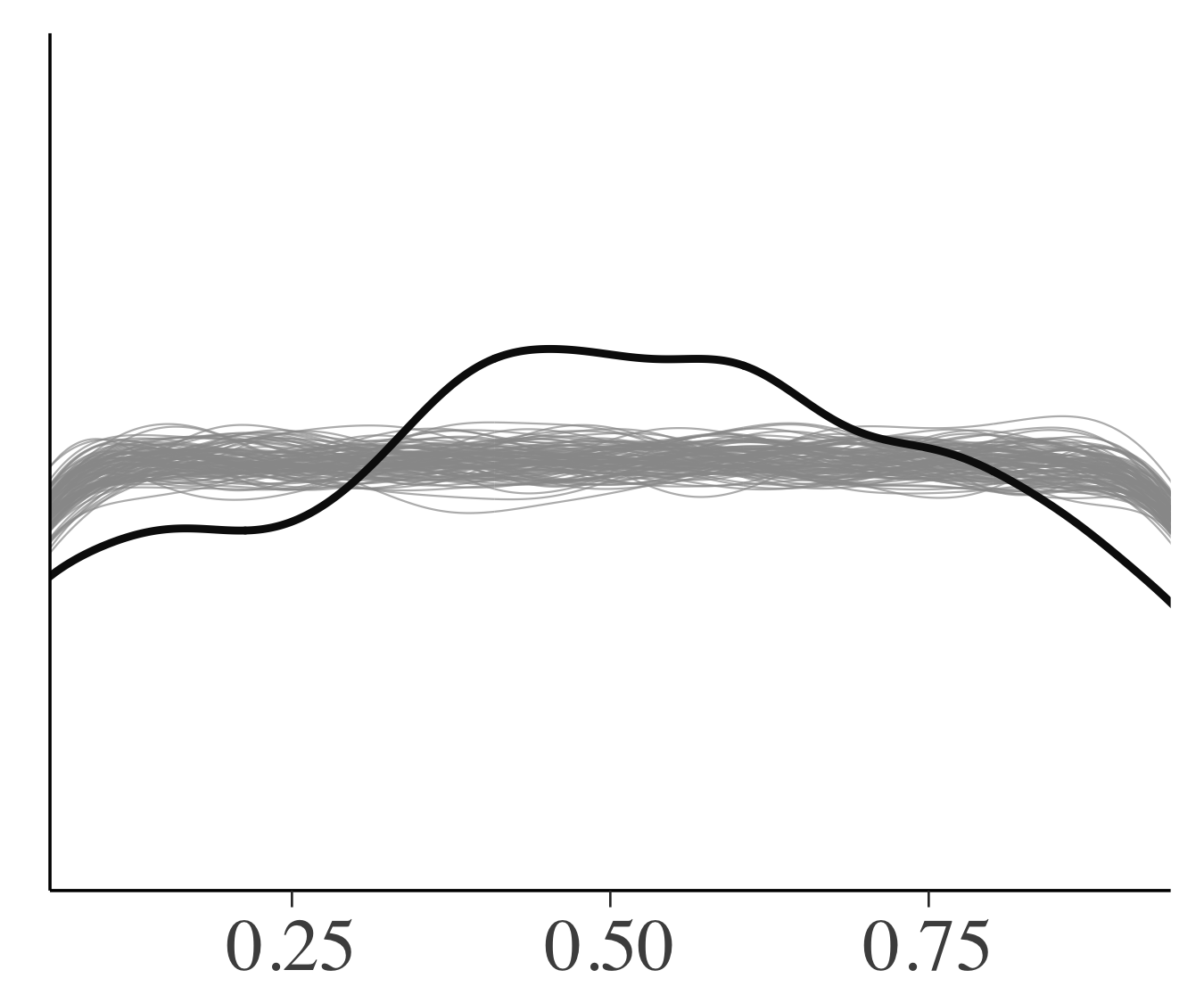 モデル2 モデル2 |
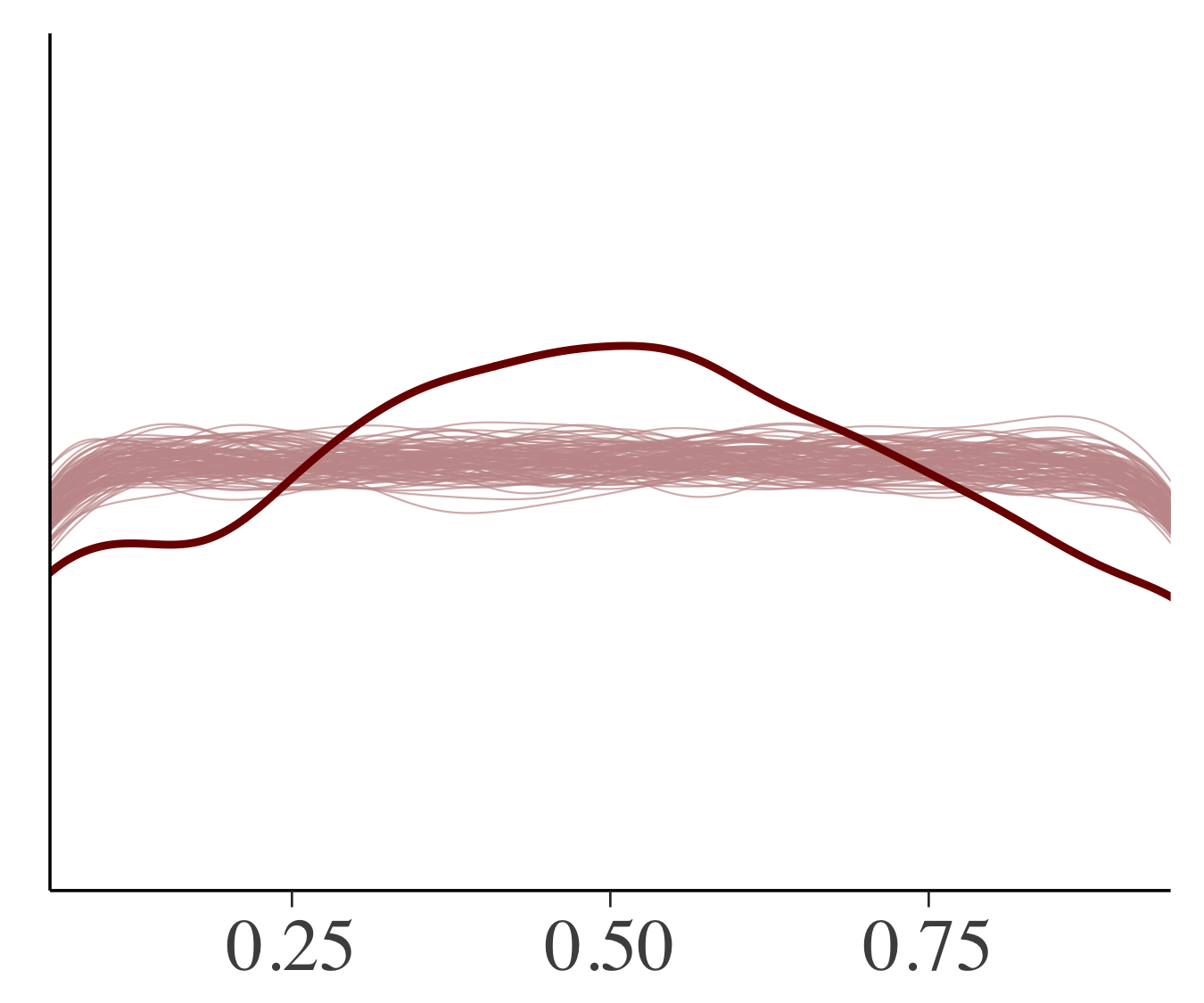 モデル3 モデル3 |
外れ値のチェック
事後予測分布のチェックを視覚的に行うことは普通でない値(外れ値でかつレバレッジが高い)の識別にも役立ちます.実際にこのような値を検証することは,統計モデルをどのように変更したらいいか(非線形モデルを使うか,裾の厚い分布を使うか)など,統計分析のワークフローにおいて重要なステップになります.
まずLOOCVにおける対数予測密度を計算することで予測することが難しいデータポイントを見つけます.またこのアプローチは予測しにくいデータポイントを一番うまく予測することができるモデルを探すことにも使えます.下図はモデル3の対数予測密度の期待値(ELPD)からモデル2のそれを引いたものになります(0よりも大きければモデル3がよい).ここではRのlooパッケージを使用しています.図では全体的にモデル3のほうが少し良さそうな感じですが,モンゴル(MNG)の予測に関してはモデル3がかなり良いという結果になっています.

looパッケージを利用する別の利点として,各一個抜きのLOO予測分布とフルデータの予測分布がどれほど近いかを表す指標($\hat{k}$)を自動的に推定してくれることが挙げられます.あるLOO予測分布の$\hat{k}$が大きい場合,そこで抜かれたデータポイントは影響が大きいものであることを意味します.最後に下図ではPM2.5のデータに対してモデル2のもとで$\hat{k}$を計算した結果になります.右上の$\hat{k}$が大きなデータポイントはモンゴルのものに対応してあり,1つ前の図でも示されているように,このデータポイントはモデル2の事後分布に対して大きな影響を持っていることを表しています.一方でモデル3のもとでのモンゴルの$\hat{k}$は0.5程度となっており,やはりこのデータポイントについてはモデル3のほうがうまく対処できることが言えます.

最後に
ベイズ分析において視覚化といえば,とりあえずMCMCのトレースプロットや自己相関関数を描く!というイメージが強いかもしれませんが,ベイズワークフローにおいて
- モデル構築の糸口となる
- アルゴリズムの挙動に問題がないかをチェックする
- モデルの比較を行う
- 影響のあるデータポイントを識別する
といったように,データ分析の最初から最後のステップまで視覚化を用いることで分析の質のチェックおよびその改善を繰り返し行っていくことができます.
一緒にお仕事しませんか!
株式会社Nospareではベイズ統計学に限らず統計学の様々な分野を専門とする研究者が所属しており,新たな知見を日々追求しています.統計アドバイザリーやビジネスデータの分析につきましては弊社までお問い合わせください.インターンや正社員も随時募集しています!
