はじめに
こんにちは,株式会社Nospareの小林です.本記事ではカウントデータ分析でよく直面するゼロが多いに対して,どのような統計モデルで対処できるかについて解説します.
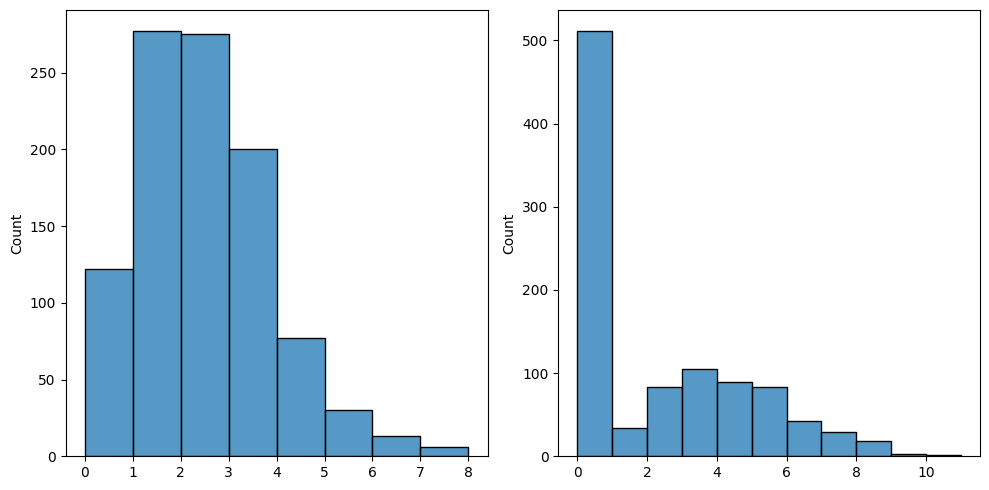
まずカウントデータですが,これはある疾病からの死亡者数,ある地点・地域における交通事故の数,個人が救急車を利用した回数などといったようにあるイベントが起こった回数に関するデータで,通常非負の整数値を取ります.例えば救急車の例でいうと多くの人は救急車を利用するという事態に直面するということは珍しいことだと考えられます.そういった場合,データはゼロ(救急車を全く利用しなかった)の値が多く含まれることになります.例えば,下図は同じサンプルサイズ($n=1000$)でほぼ同じ平均(左:2.0,右1.94)を持つ2つのカウントデータのヒストグラムになります.両方ともゼロの度数が大きいのですが,右図のほうがサンプルサイズに対するゼロの割合がかなり高くなっています(左:122,右:511).
このような状況はゼロ過剰(zero inflation)と呼ばれます(zero-modifiedとも呼ばれたりします).カウントデータに対する統計モデルはポアソン分布や負の二項分布に基づいたものが代表的ですが,ゼロ過剰が起こっているデータに対してこれらのモデルをそのまま適用するのは適切ではなく,ゼロ過剰の構造を明示的に考慮したモデルを適用必要があります.本記事ではそのようなデータに対して以下の2つのアプローチ
- ハードルモデル
- ゼロ過剰モデル
を紹介します.いずれのモデルも,ゼロが観測される構造とカウントが観測される構造の2つの部分から構成され,two-partモデルなどとまとめて呼ばれることがあります.
ハードルモデル
ハードルモデルはゼロの一点分布と正のカウント分布の混合モデルとして与えられます.具体的には確率$1-\pi$でゼロが観測され,確率$\pi$でゼロが打ち切られた離散分布に従います:
\begin{split}
\Pr(Y=0)=1-\pi,\quad 0\leq\pi\leq 1\\
\Pr(Y=y)=\frac{\pi p(y;\theta)}{1-p(0;\theta)},\quad y=1,2,\dots
\end{split}
ここで$p(y;\theta)$は正のカウントに対する確率分布(ここではベース分布と呼びます)の確率関数で,ポアソン分布などが用いられます.$1-p(0;\theta)$で割っているのは,ゼロを打ち切っているので,$\sum_{y=1}^\infty \Pr(Y=y)=\pi$となって$\sum_{y=0}^\infty \Pr(Y=y)=1$となるように基準化しています.ベース分布の平均と分散をそれぞれ$\mu$と$\sigma^2$で表記すると,ハードルモデルの平均と分散は
E[Y]=\eta=\frac{\pi\mu}{1-p(0;\theta)},\quad V(Y)=\eta(\mu-\eta)+\frac{\pi\sigma^2}{1-p(0;\theta)}
で与えられます.ベース分布をポアソン分布とすると,ポアソンハードルモデルは
\begin{split}
\Pr(Y=0)=1-\pi,\quad 0\leq\pi\leq 1\\
\Pr(Y=y)=\pi\frac{\theta^ye^{-\theta}}{y!1-e^{-\theta}},\quad y=1,2,\dots
\end{split}
と書くことができます.
ハードルモデルは名前の通り,ゼロというハードルを超えないと正のカウントが観測されない構造になっています.
ゼロ過剰モデル
ゼロ過剰モデルもハードルモデルととても似た構造を持ちます.ハードルモデルではゼロとゼロが打ち切られた分布の混合分布でしたが,ゼロ過剰モデルではゼロと打ち切りのない分布の混合となります:
\begin{split}
\Pr(Y=0)=(1-\phi) + \phi p(0;\theta),\quad 0\leq\pi\leq 1\\
\Pr(Y=y)=\phi p(y;\theta),\quad y=1,2,\dots
\end{split}
ポアソン分布を使ったゼロ過剰ポアソン(ZIP;zero-inflated Poisson)モデルは
\begin{split}
\Pr(Y=0)=(1-\phi) + \phi e^{-\theta},\quad 0\leq\pi\leq 1\\
\Pr(Y=y)=\phi \frac{\theta^y\exp^{-\theta}}{y!},\quad y=1,2,\dots
\end{split}
このモデルでは,ゼロが観測された場合でもそれはポアソン分布から生成されたゼロである可能性もありますし,固定のゼロである可能性もあります.特に後者の方は構造的なゼロ(structural zero)とも呼ばれます.
どちらのモデルを使ったらよいのか
ハードルモデルとゼロ過剰モデルの差はささいなものではありますが,分析の目的やドメイン知識に基づいて適切なモデルを選択することになります.上述の通り,ゼロ過剰モデルではたまたまゼロが観測されただけ(チャンスゼロ)の可能性と構造的なゼロが観測された可能性の両方があります.例えば過去一年に違法行為を行った回数のデータを例として考えると,絶対に違法行為は行わないということは構造的なゼロに対応し,違法行為は普通に行うけれどもデータの観測期間内にはたまたまそれがなかったということはチャンスゼロに対応します.ゼロ過剰モデルのパラメータ$\phi$はアクセス確率とも呼ばれ,例えば違法薬物などへのアクセスがそもそもない場合に確率$1-\phi$で構造的なゼロが観測される,というように解釈できます.
一方で,例えば精神科外来のようにすべての人がそれにアクセスを持つと考えらる場合で,分析の関心が外来を使わないことを選択(ゼロが観測される)あるいは1回以上使うことを選択するという構造にある場合には,ゼロの意味が一意であるのでハードルモデルが適切だと考えられます.ただし,患者が疾患を持っているかもしれない(at-risk)と知覚したあとでそのような医療サービスを求める場合には,ゼロのもつ意味が2つになる(そもそもat-riskではない,at-riskであるがサービスを利用しない)ためゼロ過剰モデルが適切であると考えられます.
回帰モデルへの拡張
ベース分布の平均や$\pi$や$\phi$などの確率を説明変数を使ってモデリングすることができます.例えばポアソン分布がベース分布の場合,対数リンクを通して$\theta = \exp(x'\beta)$とすることができます.$\pi$や$\phi$についてはロジットリンクを通して$\pi=1/(1+\exp(-x'\gamma))$とできます.モデルの推定はEMアルゴリズムに基づく最尤推定や,MCMCを使ったベイズ推定が一般的に行われています.
ZIPのPythonでの簡単な実装例
ではZIPのPythonのstatsmodels.apiを使って簡単にシミュレーションしてみます.サンプルサイズ1000,$N(0,0.3^2)$に従う説明変数を一つ,構造的なゼロを取る確率(上の説明と逆になっていますので注意)の係数を$(-1,1)$,ポアソン平均の係数を$(1.5,1)$とし,以下のコードでデータを生成しました.
import numpy as np
import statsmodels.api as sm
np.random.seed(3)
N = 1000
# 説明変数N(0,0.3^2)
x = np.random.normal(scale=0.3, size=N)
# ここでは構造的なゼロを取る確率をphiとしている
phi = 1.0 / (1.0 + np.exp(-(-1+x)))
# ポアソン平均
lam = np.exp(1.5 + x)
# 構造的なゼロかどうかを決定
u = np.random.uniform(size=N)
r = phi < u
# 構造的なゼロでない場合はポアソンから生成
y = np.zeros(N)
y[r] = np.random.poisson(lam=lam[r], size=sum(r))
これで生成されたデータの平均は$3.28$,ゼロの割合は約30%で,ヒストグラムは以下のとおりです.
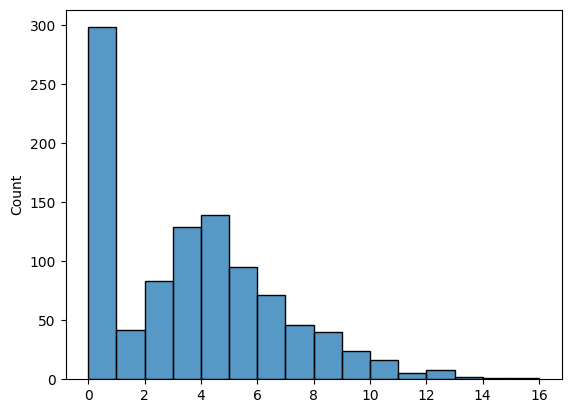
まずこのデータに対して通常のポアソン回帰を当てはめてみます.
x = sm.add_constant(x)
poi = sm.Poisson(endog=y, exog=x)
res_poi = poi.fit()
print(res_poi.summary())
以下が結果となります.ポアソンの平均の係数の真値は$(1.5,1)$であるのに対し最尤推定値は$(1.157,0.755)$と,バイアスがある結果になっています.ゼロ過剰があるデータに対しては通常のポアソン回帰モデルは不適切であることがわかります.
Optimization terminated successfully.
Current function value: 2.668203
Iterations 5
Poisson Regression Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: Poisson Df Residuals: 998
Method: MLE Df Model: 1
Date: Fri, 12 May 2023 Pseudo R-squ.: 0.03095
Time: 16:16:11 Log-Likelihood: -2668.2
converged: True LL-Null: -2753.4
Covariance Type: nonrobust LLR p-value: 5.921e-39
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 1.1570 0.018 64.323 0.000 1.122 1.192
x1 0.7545 0.058 13.049 0.000 0.641 0.868
==============================================================================
一方でちゃんとZIPを推定してみると,
# 引数exog_inflで構造的なゼロに対するロジットモデルの説明変数を指定
zip = sm.ZeroInflatedPoisson(endog=y, exog=x, exog_infl=x)
res_zip = zip.fit()
print(res_zip.summary())
以下のような結果となり,ロジットの係数の推定値は$(-0.970,1.141)$,ポアソン平均の係数の推定値は$(1.490, 1.076)$というように真値に近いものとなっています.最大対数尤度を見ても,通常のポアソン回帰は-2668なのに対してZIPは-2032と,ZIPが優れていることがわかります.
Optimization terminated successfully.
Current function value: 2.032479
Iterations: 17
Function evaluations: 19
Gradient evaluations: 19
ZeroInflatedPoisson Regression Results
===============================================================================
Dep. Variable: y No. Observations: 1000
Model: ZeroInflatedPoisson Df Residuals: 998
Method: MLE Df Model: 1
Date: Fri, 12 May 2023 Pseudo R-squ.: 0.07460
Time: 16:16:12 Log-Likelihood: -2032.5
converged: True LL-Null: -2196.3
Covariance Type: nonrobust LLR p-value: 3.031e-73
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
inflate_const -0.9696 0.076 -12.712 0.000 -1.119 -0.820
inflate_x1 1.1409 0.262 4.350 0.000 0.627 1.655
const 1.4900 0.019 79.922 0.000 1.453 1.527
x1 1.0751 0.060 17.962 0.000 0.958 1.192
=================================================================================
おわりに
ゼロ過剰はカウントデータの分析ではよく起こる現象であり,明示的に対処する必要があります.本記事の作成にあたって
Neelon et. al. (2016) Modeling zero-modified count and semicontinous data in health services research, Part 1: background and overview. Statistics in Medicine, 35, 5070--5093.
というレビュー論文を参考にしました.この論文では主に医療サービスの文脈が取り上げられています.またこのレビュー論文の続編として以下のケーススタディに特化したものがありますので興味を持たれたようでしたら参考にしてください.
Neelon et. al. (2016) Modeling zero-modified count and semicontinous data in health services research, Part 1: case studies. Statistics in Medicine, 35, 5094--5112.
一緒にお仕事しませんか!
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しており,新たな知見を日々追求しています.統計アドバイザリー,ビジネスデータの分析,データサイエンス研修・セミナーにつきましては弊社までお問い合わせください.