こんにちは,株式会社Nospareリサーチャー・千葉大学の小林です.有限混合モデルはデータのモデルベースのクラスタリングや確率密度分布を柔軟に近似するためによく用いられる重要な統計学的手法のひとつです.本記事では有限混合モデルにおけるクラスター数について特にベイズ統計学でどのように扱うか紹介したいと思います.
有限混合モデル
まず有限混合モデルは次のように表記されます.
p(y|\theta,\pi)=\sum_{j=1}^K\pi_j p(y|\theta_j)
ここで$K$はクラスター数,$\theta=(\theta_1,\dots,\theta_K)$,$p(y|\theta_j)$はパラメータ$\theta_j$をもつ$j$番目のクラスターの確率(密度)関数,$\pi_j$は$j$番目のクラスターのウェイトです($0\leq\pi_j\leq 1, \sum_{j=1}^K\pi_j=1$).$p(y|\theta_j)$の選択としては正規分布,$t$分布,ポアソン分布など応用上の問題に応じて選択されます.$p(y|\theta_j)$,$\pi_j$および$K$の組み合わせによってこのモデルは様々な形状を表現することができます.所与のクラスター数$K$のもとで,パラメータ$\pi=(\pi_1,\dots,\pi_K$),$\theta$は最尤法では例えばEMアルゴリズム,ベイズではデータ拡大法(data augmentation)によるMCMCによって推定することができます.
クラスター数の選択は重要だけど大変
有限混合モデルを有効に利用するために,$K$の選択は非常に重要な事項になってきます.$K$が小さすぎると対象の分布の形状や構造をちゃんと捉えきれないのに対し,$K$が大きすぎると不要な要素を推定する必要があるため全体的な推定の効率が低下してしまいます.ですので何らかの方法で$K$を特定することが必要なのですが,混合モデル特有の問題のせいで理論・応用両方においてなかなか難しい問題であり,これまでに様々な研究が行われてきました.
混合モデルはクラスターのラベル$j$の張替えに対して不変という性質をもっています.つまり各クラスターをどのような順番に並び替えても($K!$通りあります)同じ尤度関数を表現できるということです.またわざと大きな$K$(オーバーフィッティング)を設定してもウェイトを$\pi_j=0$とするか,あるいはクラスターのパラメータを同じ値$\theta_i=\theta_j, \ i\neq j$にする(ダブらせる)ことで,もっと少ない$K'$個($K'<K$)のクラスター数で表現されるモデルも再現することができてしまいます.
真のクラスター数を$K^{*}$とします.もし$K=K^{*}$の場合には最尤推定量は一致性をもち漸近正規性をもちます.またベイズにおける周辺尤度(エビデンス)も漸近的に通常のモデルのように振る舞います.一方で,オーバーフィッティング($K>K^{*}$)させた場合には上述の冗長な表現による特異性を考慮しなければならず,通常のAIC,BICなどは利用できません.ベイズファクター(ここではクラスター数$K^{*}$のモデルと$K$のモデルの周辺尤度の比)も$K < K^{\*}$の場合には$K^{\*}$を$N\rightarrow \infty$で指数的に大きくなりますが,$K>K^{*}$の場合には大きなモデルに対する罰則がかなり遅くなります(多項式的).
クラスター数をパラメータとして扱って推定する?
ベイズ統計学の枠組みでは$K$を新たなパラメータとして扱い,これに事前分布$p(K)$を仮定して$K$の事後分布$p(K|Y)$から$K$の推定値を得るということも可能です.ただし当然$K$の事後分布は解析的に得られないのでMCMCによるサンプリングが必要になってくるのですが,$K$のサンプリングにおいてたとえば$K=k\rightarrow K=k+1$というムーブがあったときに,$K=k$のときにはなかった$\theta_{k+1}$や$\pi_{k+1}$を作って,MCMCのステップの実行前後でモデル間($K$の値が変わる)の次元を合わせてやる必要があります.このような調整を行うMCMCをtransdimensional MCMCと呼んだりし,Reversible Jump MCMC(RJMCMC),birth-and-deathアルゴリズムがよく知られていますが,場合によって,共役事前分布しか使えない,実装やチューニングが面倒,アルゴリズムの事後分布への収束が遅いという問題が知られています.
ディリクレ過程混合モデルによるクラスター数の推定はうまくいかない
ディリクレ過程混合モデルはクラスター数無限の混合モデルとして書けます.
p(y|\theta)=\sum_{k=1}^\infty w_k p(y|\theta_k),
ここでウェイト$w_k$はスティックブレーキング(stick breaking)と呼ばれる表現で与えられます.推定自体はスライスサンプリングを組み合わせることで無限和を有限和で切って(近似せずに!),通常の有限混合モデルに対するMCMCに追加的なステップを加えた方法で推定できます.
モデル上でのクラスター数は無限ですが,データは有限個のクラスターに割り当てられます.ディリクレ過程の性質として空でないクラスター数$K^+$は$O(\alpha \log N)$で増えていき($N$は標本数,$\alpha$はディリクレ過程のパラメータ),データ数が大きくなるにつれて推定されるクラスター数が増えていきます.そして,ひとつのデータポイントからなるクラスターがたくさん生成され,各クラスターのサイズがどんどん小さくなっていくということが経験的に知られています.実際のところ,真のデータ生成過程がクラスター数$K^{*}$の有限混合モデルであるときにはディリクレ過程混合モデルで得られた推定値$K^+$は一致性を持ちません(Miller and Harrison, 2013).
簡単な方法:Sparse Dirichlet Priorでいらないクラスターのウェイトをゼロにしてしまう!
有限混合モデルのベイズ推定においては通常$\pi$に対してディリクレ事前分布を仮定します:
p(\pi|\alpha) \propto \prod_{j=1}^K \pi_j^{\alpha_j-1},
$\alpha=(\alpha_1,\dots,\alpha_K), \alpha_j>0$はディリクレ分布のパラメータで,分析者が設定します.このディリクレ事前分布は条件付共役であるので,ギブスサンプラーによるMCMCが簡単にまわせます.
そんなディリクレ事前分布に対して,Rousseau and Mengersen (2011)は次の重要な理論結果を導いています.
- $\max_j {\alpha_j} < d/2$のとき,$\pi$の事後分布は冗長なクラスターに関してはゼロになる(ダブりのクラスターはひとつにまとめる)
- $\min_j{\alpha_j }>d/2$のとき,$\pi$の事後分布は少なくともふたつのクラスター$i, j (i\neq j)$について$\theta_i=\theta_j$となり,$\pi_i>0, \pi_j>0$となる(ダブりのクラスターができる)
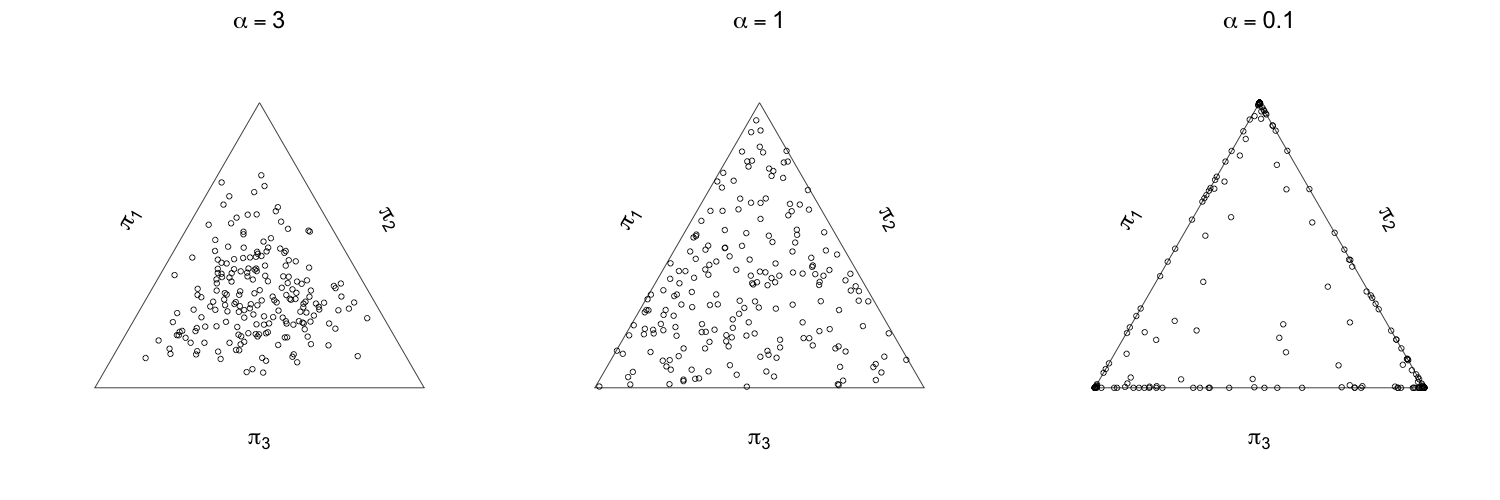
ここで$d$は有限混合モデルの各クラスターのパラメータの数とします.この結果が意味することろは大きな$K$(オーバーフィッティング)と十分に小さな$\alpha_j$の値(sparse Dirichlet)を設定することで,空のクラスターを作り出してそのクラスターのウェイトをゼロにしていくということが可能になる,ということです.この結果はあくまでも漸近的なものなので,有限の標本数しかない現実問題ではもっと小さな値を設定したほうがよいです.普段ディリクレ事前分布を使う場合には各$\alpha_j$の値は同じもの$\alpha$(対称ディリクレ分布)を使うことが多いですが,実用上は$\alpha$が$1$よりも十分小さな値(例えば$0.01$)を使うとスパース性を発揮できます.下記の図は各$\alpha$の値のもとでディリクレ分布から乱数を発生させたプロットです.$\alpha=0.1$の場合にはほとんどの点が三角形(2-シンプレックス)のふちにあり,これはすくなくともひとつの$\pi_j$の値がゼロに近いということを意味しています.一方で$\alpha=1$の場合には三角形の内部にまんべんなく点在(一様分布),$\alpha=3$のときには中央に分布しています.
より強いスパース性を導入:Non-Local Prior
Sparse Dirichlet Priorのスパース性はクラスターウェイトについてだけです.より強くスパース性を有限混合モデルに導入するために,Fu ́quene etal. (2019)は次のようなスパース性をもつNon-Local Prior(NLP)を提案しました.この事前分布は,次のいずれかの状況
- 任意のクラスターに対して$\pi_j\rightarrow 0$(クラスターのウェイトがゼロになる)
- 任意の$i\neq j$に対して$\theta_i\rightarrow \theta_j$(ダブりのクラスターができる)
の極限において,クラスター数$K$のもとでの事前密度$p(\theta,\pi|K)$がゼロになる,というように設計されています.具体的には,
p(\vartheta|K)\propto d(\vartheta)p^L(\vartheta|K)
という形で,$\vartheta=(\theta,\pi)$,$d(\vartheta)$は上の2つ目の状況でゼロに収束するような関数,$p^L(\vartheta|K)$はこの論文ではLocal Prior(LP)と呼ばれる通常の(NLPを使わない)分析で使用する$\theta$や$\pi$の事前分布(例えば正規分布やディリクレ分布など)です.さらに,$d(\vartheta)=d(\theta)d(\pi)$,$p^L(\vartheta|K)=p^L(\theta|K)p^L(\pi|K)$としています.NLPのうちウェイトにかかる部分は$p(\pi|K)=Dir(\pi|\alpha)\propto d(\pi)Dir(\pi|\alpha-r)$で,ここで$Dir$は対称ディリクレ分布を表し,$\alpha>1$です.
NLPに対する理論的な結果としては,とある$K$のもとで
- $K\leq K^{*}$のとき,$d(\vartheta)$のLPのもとでの事後分布はある定数に収束する
- $K>K^{*}$のとき,$d(\vartheta)$のLPのもとでの事後分布はゼロに収束する
NLPのもとでの周辺尤度は$p(y|K)=p^L(y|K)E^L[d(\vartheta)|y]$で表されます.ここで$p^L(y|K)$はLPのもとでの周辺尤度,$E^L[d(\vartheta)|y]$はLPのもとでの$\vartheta$の事後分布での$d(\vartheta)$の期待値を表します.NLPのもとでは,オーバーフィッティングした混合モデルの周辺尤度はゼロに収束し強くペナルティを受ける,という結果になっています.
$d(\theta)$の形状は,例えばクラスターの分布が正規分布$N(\mu_j,\Sigma_j)$の場合には通常平均パラメータについて関心があるので
d(\mu)\propto \prod_{1\leq i<j\leq K} (\mu_i-\mu_j)^t A^{-1}(\mu_i-\mu_j)/g
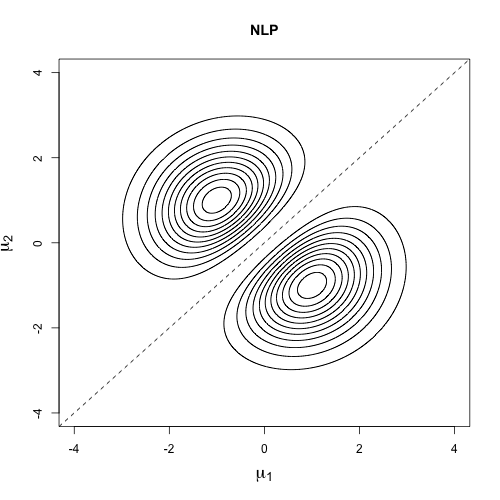
などが考えられます.下の図は$K=2$で1次元の場合の$p(\mu|K)$の等高線です.この例では事前分布は二峰で,45度線($\mu_1=\mu_2$)上では事前密度がゼロになっていてクラスターがダブるようなパラメータの値に対して強いペナルティがかかっていることが示されています.
この論文では事後分布からのサンプリング方法やベイズファクターの計算方法など,NLPに基づいた推測・解析について詳細に書かれています.またRパッケージmombfやNLPmixも公開されています.
一緒にお仕事しませんか!
株式会社Nospareではベイズ統計学に限らず統計学の様々な分野を専門とする研究者が所属しており,新たな知見を日々追求しています.統計アドバイザリーやビジネスデータの分析につきましては弊社までお問い合わせください.