株式会社Nospareの小林、段、奥田です。
今回は、時系列データを用いて広告効果を推定するメディア・ミックス・モデリング(MMM: Media Mix Modeling)について紹介します。本記事では、Googleが開発したフレームワークの基本概念を解説し、最新のパッケージである Meridian を活用した分析ワークフローを詳しく説明します。具体的には、MMMの基本から、Meridianを用いた実装・分析・最適化のプロセスまでを順を追って解説します。
1. MMMの基本
メディア・ミックス・モデリング(MMM: Media Mix Modeling) は、複数の広告チャネルやプロモーション施策の費用対効果を定量化し、限られた予算をどの広告にどの程度配分すべきかを分析する手法です。MMM により、以下のような疑問にアプローチできます。
- どの広告チャネル(新聞、テレビ、YouTube、Facebook など)が売上にどの程度寄与しているのか?
- 各チャネルの ROI(費用対効果)はどの程度か?
- 次期の広告予算をどのチャネルにどのように配分すれば効果的か?
この手法は、1964 年にハーバード・ビジネス・スクールの Neil H. Borden によって提案され[1]、アメリカのマーケティング学者 Edmund J. McCarthy によって普及しました[2]。近年では、ベイズ統計のアプローチ を取り入れることで、事前知識の活用や不確実性の定量化が可能となり、従来の最尤法では対応が難しかった課題にも柔軟に対処できるようになっています[3]。
メディア・ミックス・モデルの基本構造
MMM では、売上などの KPI を次のように 加法的に分解 できることを仮定します。
$$
\text{売上} = \text{基礎売上} + \sum\text{媒体効果} + \sum\text{外部要因} + \text{誤差}
$$
ここで、各項の意味は以下のとおりです。
- 基礎売上: 広告を全く打たなかった場合の売上
- 媒体効果: 各広告チャネルへの投資が売上に与える影響
- 外部要因: 季節性、市場動向、競合の影響など、広告以外の要因による売上への影響
- 誤差: 予測不能な変動(ランダムノイズ)
Google が開発したMMMフレームワークの特徴
Google の研究チームが研究・開発した MMM のフレームワークでは、広告効果をモデル化する際に二つの仮定を置いています。
- 残存効果(Carryover Effect): 広告の効果は、広告を打った時点だけではなく、将来にもわたって効果が持続する。
- 飽和効果(Saturation Effect): 広告の効果は最初は大きく増加するが、一定以上の投資をすると飽和し、追加の投資による効果が逓減する。
残存効果 Carryover Effect
広告の効果は、広告を打った時点だけではなく、しばらくその効果が持続することが一般です(例: 広告を見た後にしばらく消費者の記憶に残る)。この現象をモデル化するために、adstock 関数(過去の広告投入量に対する残存効果を考慮した加重平均)を用います。
表記
- $t$: 時点 (日時または週次)
- $x_t$: 時点 $t$ における広告投入量
- $l$: ラグ (遅延の度合い)
- $w(z)$: 重み関数
広告投入量 $x_t$ に対する遅延効果を考慮した adstock 関数 は、以下のように定義されます。
$$
\text{adstock}(x_{t-L+1},\ldots,x_t; w, L) = \frac{\sum_{l=0}^{L-1} w(l) x_{t-l}}{\sum_{l=0}^{L-1} w(l)}
$$
ここで、$w(l)$ は広告効果の時間変化を決定する重み関数です。広告の影響が時間とともに減衰しつつも一定期間持続する特性を考慮し、以下の広告効果が一定割合で減衰するモデルが使用されます。
$$
w(l; \alpha) = \alpha^l, \quad l = 0,\ldots,L-1, \quad 0 < \alpha < 1
$$
- 特徴
- 広告効果が指数関数的に減衰(例: TVCM のように、視聴後すぐに効果が落ちるが、しばらくは影響が続く)
- パラメータ $\alpha$ は "保持率" を表し、$\alpha$ が大きいほど広告効果が長く持続する
- 計算が容易
import numpy as np
def geometric_delay(lags, alpha):
assert 0 < alpha < 1, "alpha must be between 0 and 1"
return alpha**lags
def adstock(x, weight_type, L, *args, mode='valid', **kwargs):
lags = np.arange(L)
weights = geometric_delay(lags, *args, **kwargs)
weights = weights[::-1]
weights_norm = weights / np.sum(weights)
result = np.convolve(x, weights_norm[::-1], mode=mode)
return result
def random_walk(init_value, steps, seed):
np.random.seed(seed)
return np.cumsum(np.random.randn(steps)) + init_value
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("whitegrid")
lags = np.linspace(0, 20, 200)
y = geometric_delay(lags, 0.8)
fig, ax = plt.subplots(figsize=(15, 6), ncols=2)
ax[0].plot(lags, y, label="geometric delay")
ax[0].legend()
t = np.arange(100)
y = random_walk(0, len(t), 0)
L = 10
adstock = adstock(y, 'geometric_delay', L, 0.8)
ax[1].plot(t, y, label="random walk")
ax[1].plot(t[L-1:], adstock, label="geometric delay")
ax[1].legend()
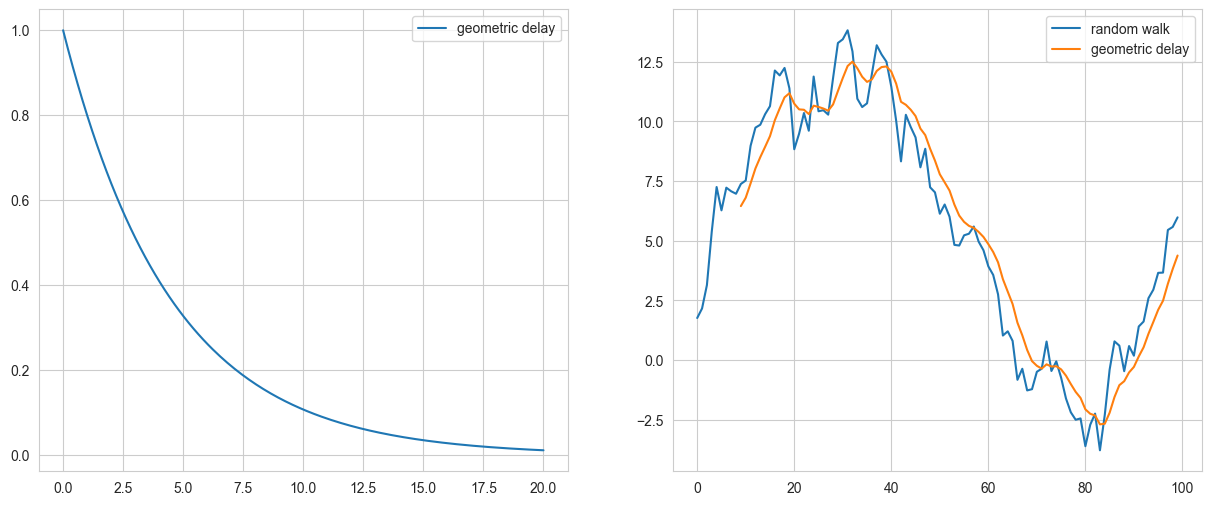
左側のプロットは Geometric delay 関数を可視化したものです。広告効果がすぐにピークに達し、その後指数関数的に減衰します。右側のプロットは Geometric delay 関数を時系列データに適用したものです。シグナルを遅延させると共に多少滑らかにする効果があることが確認できます。
ここまでは理解を促すためと表記を簡潔にするため、一つのチャネルしかない場合のケースを解説しましたが実際は複数のチャネル($M$ 個)に対して、それぞれ異なる adstock 関数を適用し、各チャネル $m$ の広告投入量の残存効果を推定します。
一般形として、チャネル $m$ における adstock 関数 は以下のように定義されます:
$$
\text{adstock}(x_{t-L+1,m},\ldots,x_{t,m}; w_m, L) = \frac{\sum_{l=0}^{L-1} w_m(l) x_{t-l,m}}{\sum_{l=0}^{L-1} w_m(l)}。
$$
次に、広告効果の飽和効果 (Saturation Effect) について説明します。
飽和効果
広告投資による売上への影響は、初期段階では大きく増加 しますが、一定の投資額を超えると効果が頭打ち(飽和状態) になると考えられます。この 飽和効果 をモデル化する手段として、Hill 関数 が用いられます。Hill 関数はもともと化学反応の酵素活性の飽和効果を表現するために用いられていましたが、マーケティング分野においても、広告効果が限界に達する現象を適切に表現することができます。
Hill 関数は以下のように定義されています:
$$
\text{Hill}(x_t; \kappa, \eta) = \frac{1}{1+(x_t/\kappa)^{-\eta}}, \quad x_t \geq 0
$$
ここで:
- $\eta$ は形状パラメーターまたは傾きパラメータ
- 広告効果の増加速度を制御します。
- $\eta$ が大きいほど、広告の効果が急激に立ち上がる (S 字カーブが急になる)
- $\kappa > 0$ は半飽和点と呼ばれるパラメータ
- 広告効果が 50% に達する広告投入量を示します。
- $x_t = \kappa$ のとき、$\text{Hill}(x_t)$ は 0.5 になります。
この関数の特性として、$x_t$ が大きくなるにつれて $\text{Hill}(x_t)$ は 1 に近づき、広告効果が飽和することがわかります。
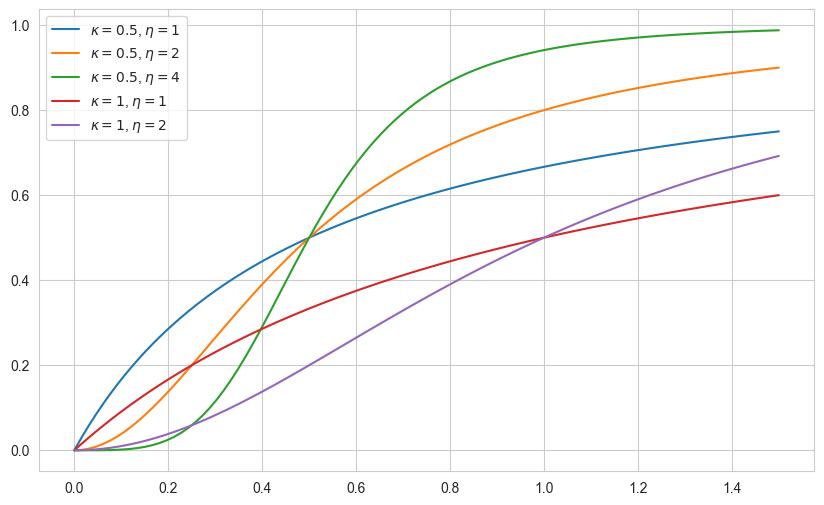
異なるパラメータ設定に対する Hill 関数の挙動を可視化します。
def hill(x, kappa, eta):
return 1 / (1 + (x / kappa + 1e-10)**(-eta))
x = np.linspace(0, 1.5, 100)
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, hill(x, 0.5, 1), label="$\kappa=0.5$, $\eta=1$")
ax.plot(x, hill(x, 0.5, 2), label="$\kappa=0.5$, $\eta=2$")
ax.plot(x, hill(x, 0.5, 4), label="$\kappa=0.5$, $\eta=4$")
ax.plot(x, hill(x, 1, 1), label="$\kappa=1$, $\eta=1$")
ax.plot(x, hill(x, 1, 2), label="$\kappa=1$, $\eta=2$")
ax.legend()
plt.show()
広告チャネルが $M$ 個ある場合、それぞれのチャネルに対して個別の Hill 関数 を推定します。さらに、各チャネルの広告効果が KPI(例: 売上やコンバージョン)に与える影響は異なるため、回帰係数 $\beta_m$ を Hill 関数に掛ける ことで、チャネルごとの影響度を考慮します。
\beta_m \text{Hill}_m(x_{t,m}) = \beta_m - \frac{\kappa_m^{\eta_m} \beta_m }{ x^{\eta_m}_{t,m} + \kappa^{\eta_m}_m}.
Adstock の Hill関数への組み込み
広告の 残存効果(Carryover Effect) と 飽和効果(Saturation Effect) を同時に表現するために、Google のフレームワークでは Hill 関数の中に adstock 関数を組み込む というアプローチを採用しています。
各チャネル $m$ の広告投入量に対して、まず adstock 関数 を適用し、時間遅延を考慮した広告投入量 $x^*_{t,m}$ を求めます。
x^*_{t,m} = \text{adstock}(x_{t-L,m}, \ldots, x_{t,m};w_m, L)
この adstock 加工済みの広告投入量 $x^*_{t,m}$ を Hill 関数に入力することで、残存効果と飽和効果の両方を同時に考慮した広告効果をモデル化できます。最終的な広告効果は、以下のように表現されます。
\beta_m \text{Hill}(x^*_{t,m}; \kappa_m, \eta_m)
2. Meridian
ここまで解説した内容は、Jinら[3]が2017年に発表した内容に基づいています。Meridianは、この内容をさらに拡張しています。
用語
Meridianのモデリングを理解するにはまず下記の用語と指標を理解することが重要になります。
非メディア活動 (Non-media treatments)
メディアへの支出を伴わないが、KPIに影響を与える可能性のあるマーケティング活動のこと。
- セールス、割引、クーポンキャンペーン
- 商品価格の調整
- プロダクトのパッケージングやデザインの変更
- 店内ディスプレイ、ロイヤリティ・プログラム、サービス提供の変更など、メディア費用と直接結びついていない行動
有料メディア (Paid-media)
広告主がお金を払って広告を表示させるチャネルのことを指す。
- デジタル広告: Google広告、ディスプレイ広告、SNS広告、動画広告
- 伝統的なメディア:テレビ広告、ラジオ広告、印刷広告、野外広告
オーガニック・メディア・チャンネル (Organic media channel)
直接的な金銭的コストをかけずにマーケティング露出を実現するチャンネルを指す。
- ニュースレター、メルマガの配信
- ブログ投稿
- SNS活動: Facebook、Twitter、Instagramなどのプラットフォームへの投稿
- メールキャンペーン: オーディエンスへの非課金メールアウトリーチ
リーチ (Reach)
指定された期間内に広告やコンテンツを実際に見たユニークな個人の数
フリークエンシー (Frequency)
それぞれの個人が平均して何回広告に接触したかの数
増分結果 (Incremental Results)
特定のメディア $m$ と期間 $[T_0, T_1]$ について、増分結果は次の様に定義されます
$$
\text{増分結果}_m = \text{メディア} m \text{に投資した場合の売上} - \text{メディア} m \text{に投資しなかった場合の売上}
$$
費用対効果 (Return of Interests; ROI)
特定のメディア $m$ と期間 $[T_0, T_1]$ について、ROIは次の様に定義されます
$$
\text{ROI}_m = \frac{\text{増分結果}_m}{投資した金額}
$$
Meridianのモデル構造
Meridian は KPI を次の様に 加法的に分解 します:
$$
\begin{align*}
\text{KPI} = \text{時間効果} + \text{地域効果} &+ \sum \text{外部要因の効果} \
&+ \sum \text{非メディアの効果} \
&+ \sum \text{有料メディア効果} \
&+ \sum \text{オーガニックメディアの効果} \
&+ \sum \text{リーチと頻度情報を含む有料メディアの効果} \
&+ \sum \text{リーチと頻度情報を含むオーガニックメディアの効果}
\end{align*}
$$
-
時間効果: Meiridanではトレンドや季節性といった効果をスプラインによって捉えようとしております。特別な休日等の効果は別途説明変数に組み込むことが可能です。
-
地域効果: Sunら(2017)が提案した GBHMMM を採用し、マーケティング施策の地域ごとの影響をモデル化しています。従来のMMMは全国レベルのデータを利用することが多く、サンプルサイズの制約やメディア支出の変動の不足といった課題がありました。GBHMMMでは、地域ごとの広告データを統合し、ベイズ階層モデリングを用いることで、各地域の広告効果をより精緻に推定できます。
-
リーチやフリークエンシーデータの利用 : Meridianでは、各メディアにおいてリーチ(広告を見た固有ユーザー数)やフリークエンシー(1人あたりの広告の平均表示回数)のデータがある場合には、それらの効果をHill/Adstock関数を使って表現することで、最適フリークエンシーやそのもとでの最適予算配分を提案することが可能です。
これらのモデリングに加えて:
-
直感的に理解しやすい事前分布の工夫: Meridianでは、ベイズ推論を用いたMMMにおいて、直感的に解釈しやすい事前分布(Prior)を設定できるようになっています。広告効果の推定には事前知識を取り入れることが重要ですが、Meridianでは、過去の業界データや広告主ごとの知見を適切に活用することで、モデルの安定性と解釈性を向上させています。
-
最適な予算配分を割り出す数理最適化手法: MMMの主要な目的の一つは、広告予算を最適に配分することです。Meridianでは、ROI(Return on Investment, 投資利益率)などを最大化する広告予算の配分を提案できます。MMMの出力結果から得られるROAS(Return on Ad Spend, 広告投資利益率)や mROAS(Marginal ROAS, 限界広告投資利益率)を活用し、各広告チャネルへの最適な支出バランスを求めることが可能です。
-
計算の大幅な高速化: MMMは通常、マルコフ連鎖モンテカルロ法(MCMC)などの計算コストが高い推論手法を用いるため、大規模データを処理するには計算負荷が課題となります。Meridianでは、ハミルトニアン・モンテカルロ(HMC)といった高度なベイズ計算手法を活用し、計算時間を大幅に短縮しています。これにより、マーケターが迅速に分析結果を取得し、施策の最適化に活用できるようになっています。
3. Meridian を用いた広告効果分析のワークフロー
Meridianを用いた広告効果分析のワークフローは、以下のステップで構成されます。
- セットアップ
- データの読み込み
- モデルの設定
- 推論 (MCMC)
- モデルの診断
- 結果の出力
- 予算配分の最適化
- モデルの保存
0. セットアップ
Meridian は PyPI 経由でインストールできます。GPUバージョンとCPUバージョンがそれぞれ用意されていますが、Google Collab で実行することを想定してGPUバージョンをインストールします。
# GPU環境(CUDA利用)の場合
!pip install --upgrade google-meridian[and-cuda]
次に必要なパッケージを読み込みます。
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_probability as tfp
import arviz as az
import IPython
from meridian import constants
from meridian.data import load
from meridian.data import test_utils
from meridian.model import model
from meridian.model import spec
from meridian.model import prior_distribution
from meridian.analysis import optimizer
from meridian.analysis import analyzer
from meridian.analysis import visualizer
from meridian.analysis import summarizer
from meridian.analysis import formatter
# check if GPU is available
from psutil import virtual_memory
ram_gb = virtual_memory().total / 1e9
print('Your runtime has {:.1f} gigabytes of available RAM\n'.format(ram_gb))
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
print("Num CPUs Available: ", len(tf.config.experimental.list_physical_devices('CPU')))
1. データの読み込み
ここではMeridianのドキュメンテーションでも用いられている擬似データセットを使用します。
data_url = "https://raw.githubusercontent.com/google/meridian/refs/heads/main/meridian/data/simulated_data/csv/geo_all_channels.csv"
df = pd.read_csv(data_url)
df.head()
Meridian はとして次のものを入力として受け付けます。
| データタイプ | 説明 |
|---|---|
KPI (kpi) |
モデルの目的変数。例: 売上金額、インストール数 |
メディア指標 (media) |
チャンネル、地域、および期間ごとの露出指標を含みます。支出、インプレッション、クリック等、広告主が介入可能な変数。負の値を含んではいけません。 |
メディア支出 (media_spend) |
チャンネルと期間ごとの支出データ。メディアデータとメディア支出は同じ次元である必要があります。 |
制御変数 (controls) |
KPIとメディア指標の両方に因果関係を持つ交絡因子を含みます (Google検索クエリ量 (GQV) など)。 |
KPIあたりの収益 (revenue_per_kpi) |
KPI単位あたりの平均収益を含みます。収益がKPIである場合、「KPIあたりの収益」は必要ありません。 |
地域人口 (population) |
各地域の人口。すべての地域を比較できるようメディア指標を調整するために使用されます。 |
オーガニックメディア (organic_media) |
直接的なコストがかからないメディア活動に関するデータ。ニュースレターからのインプレッション、ブログ投稿、SNS活動、またはメールキャンペーンなどが含まれます。 |
非メディア変数 (non_media_treatments) |
プロモーションの実施、製品の価格、製品のパッケージまたはデザインの変更など、メディアに直接関連しないマーケティング活動のデータが含まれます。 |
まず、データフレームのどの列がどのデータタイプに対応するかを Meridian に教える必要があります。そのためには、CoordToColumns クラスを次のように使用します。
coord_to_columns = load.CoordToColumns(
time='time', # 時点
geo='geo', # 地域ID
controls=['GQV', 'Competitor_Sales'], # 制御変数
population='population', # 地域人口
kpi='conversions', # KPI (この場合はコンバージョン率)
revenue_per_kpi='revenue_per_conversion', # コンバージョンあたりの収益
media=[ # メディアデータ (インプレッション数)
'Channel0_impression',
'Channel1_impression',
'Channel2_impression',
'Channel3_impression',
'Channel4_impression',
],
media_spend=[ # メディア支出
'Channel0_spend',
'Channel1_spend',
'Channel2_spend',
'Channel3_spend',
'Channel4_spend',
],
organic_media=['Organic_channel0_impression'], # オーガニックメディア
non_media_treatments=['Promo'], # 非メディア変数
)
メディアデータとメディア支出においては、それぞれがどのメディアに対応しているのかを明示的する必要があります。その為に次の様な辞書型変数を作成します。
# メディアデータと対応するメディア
correct_media_to_channel = {
'Channel0_impression': 'Channel_0',
'Channel1_impression': 'Channel_1',
'Channel2_impression': 'Channel_2',
'Channel3_impression': 'Channel_3',
'Channel4_impression': 'Channel_4',
}
# メディア支出と対応するメディア
correct_media_spend_to_channel = {
'Channel0_spend': 'Channel_0',
'Channel1_spend': 'Channel_1',
'Channel2_spend': 'Channel_2',
'Channel3_spend': 'Channel_3',
'Channel4_spend': 'Channel_4',
}
テーブル型のデータを Meridian の入力として使えるものにするため、DataFrameDataLoader を使用します。先ほど定義して coord_to_columns、correct_media_to_channel、correct_media_spend_to_channel を引数として渡します。
loader = load.DataFrameDataLoader(
df=df,
coord_to_columns=coord_to_columns,
kpi_type='non_revenue',
media_to_channel=correct_media_to_channel,
media_spend_to_channel=correct_media_spend_to_channel,
)
data = loader.load()
これでデータの準備が完了しました。
2. モデルのカスタマイズ
各メディアの費用対効果 (ROI) に関する事前知識は、事前分布をカスタマイズすることで反映できます。ここでは、すべてのメディアにおいて、ROIが平均パラメータ 0.2 、標準偏差パラメータ0.9の対数正規分布に従うと、事前に仮定します。これは、平均ROIが 1.8 であり、その周辺に不確実性があることを意味します。ROIは負の値をとるべきではないため、対数正規分布を使用しています。
roi_mu = 0.2 # Mu for ROI prior for each media channel.
roi_sigma = 0.9 # Sigma for ROI prior for each media channel.
prior = prior_distribution.PriorDistribution(
roi_m=tfp.distributions.LogNormal(roi_mu, roi_sigma, name=constants.ROI_M)
)
model_spec = spec.ModelSpec(prior=prior)
カスタマイズ後、モデルのインスタンスを作ります。
mmm = model.Meridian(input_data=data, model_spec=model_spec)
3. 推論 (MCMC)
以下のコマンドを実行して事前分布と事後分布からサンプリングを行います。Google Collab のGPUインスタンスを使用した場合おおよそ10分かかります。
%%time
mmm.sample_prior(500)
mmm.sample_posterior(n_chains=7, n_adapt=500, n_burnin=500, n_keep=1000)
Meridian は No U-Turn サンプリング (NUTS) と呼ばれるMCMCサンプリング手法を使います。NUTSはサンプリングの質を向上させる為に自動的にMCMCのハイパーパラメータをチューニングするアルゴリズムです。ここで n_adapt はチューニングにかけるチェーン毎のサンプリング数を指定するハイパーパラメーターです。これらのサンプルは常に除外されることになります。
n_burnin はチューニング後、MCMCが定常分布に収束するまで追加で走らせるサンプリング数を指定する引数です。これらのサンプルも常に除外されます。
n_keep は実際に事後分布の推論に使うサンプル数です。
4. モデルの診断
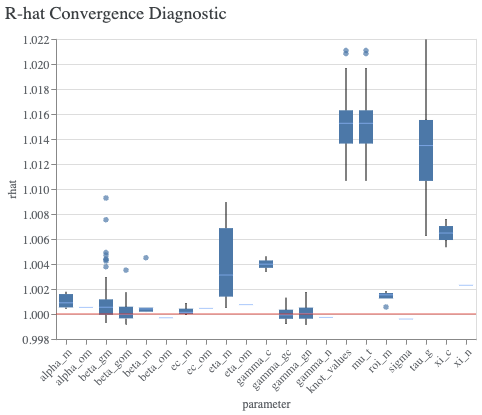
MCMCサンプリングの実行後、モデルの事後分布が適切に定常分布に収束しているかを確認することは不可欠です。収束の評価指標として、Rhat統計量が広く用いられています。一般的に、Rhat値が1.1を下回れば、事後分布が収束したと判断できます。ModelDiagnosticsクラスのplot_rhat_boxplotメソッドを使用することで簡単にモデルパラメータの Gelman-Rubin統計量 $\hat{R}$ 値を可視化することができます。
model_diagnostics = visualizer.ModelDiagnostics(mmm)
model_diagnostics.plot_rhat_boxplot()
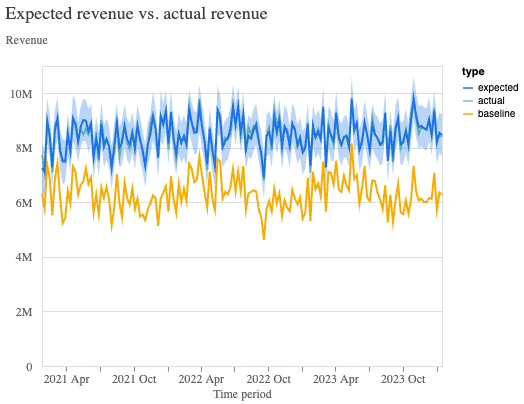
モデルのパラメーターの収束に加えて、モデルが出す期待値が実際訓練に使用したデータと似ているかを確認することも大事です。これは次のように ModelFit クラスの plot_model_fit() メソッドを利用することで簡単に行うことができます。
model_fit = visualizer.ModelFit(mmm)
model_fit.plot_model_fit()
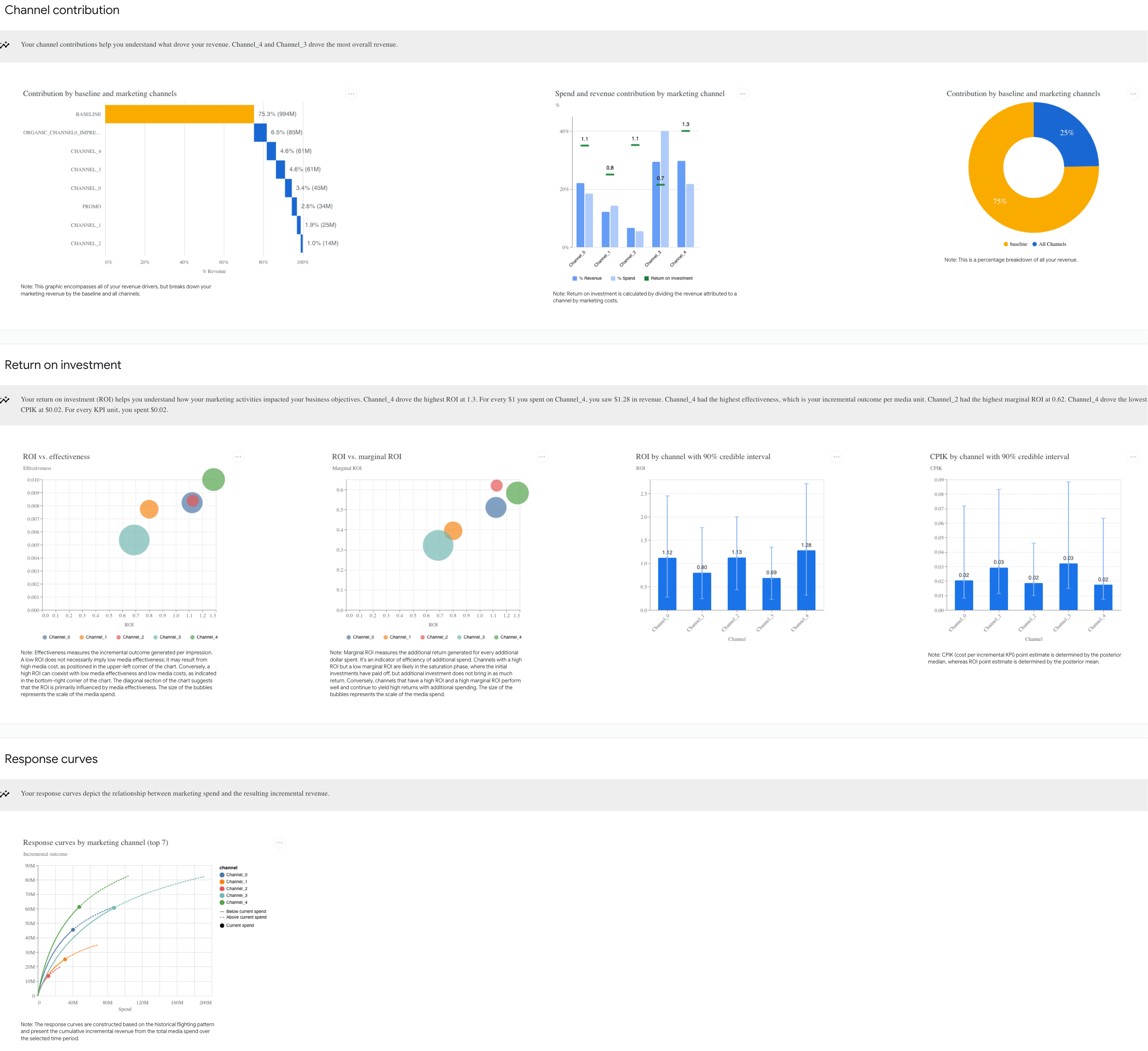
5. 結果の出力
Meridian は分析結果のレポートを生成するための機能も兼ね備えています。Summariserクラスのoutput_model_results_summaryを使用すれば簡単に2ページの分析結果レポートをhtmlとして出力してくれます。
mmm_summarizer = summarizer.Summarizer(mmm)
from google.colab import drive
drive.mount('/content/drive')
filepath = '/content/drive/MyDrive'
start_date = '2021-01-25'
end_date = '2024-01-15'
mmm_summarizer.output_model_results_summary('summary_output.html', filepath, start_date, end_date)
IPython.display.HTML(filename='/content/drive/MyDrive/summary_output.html')
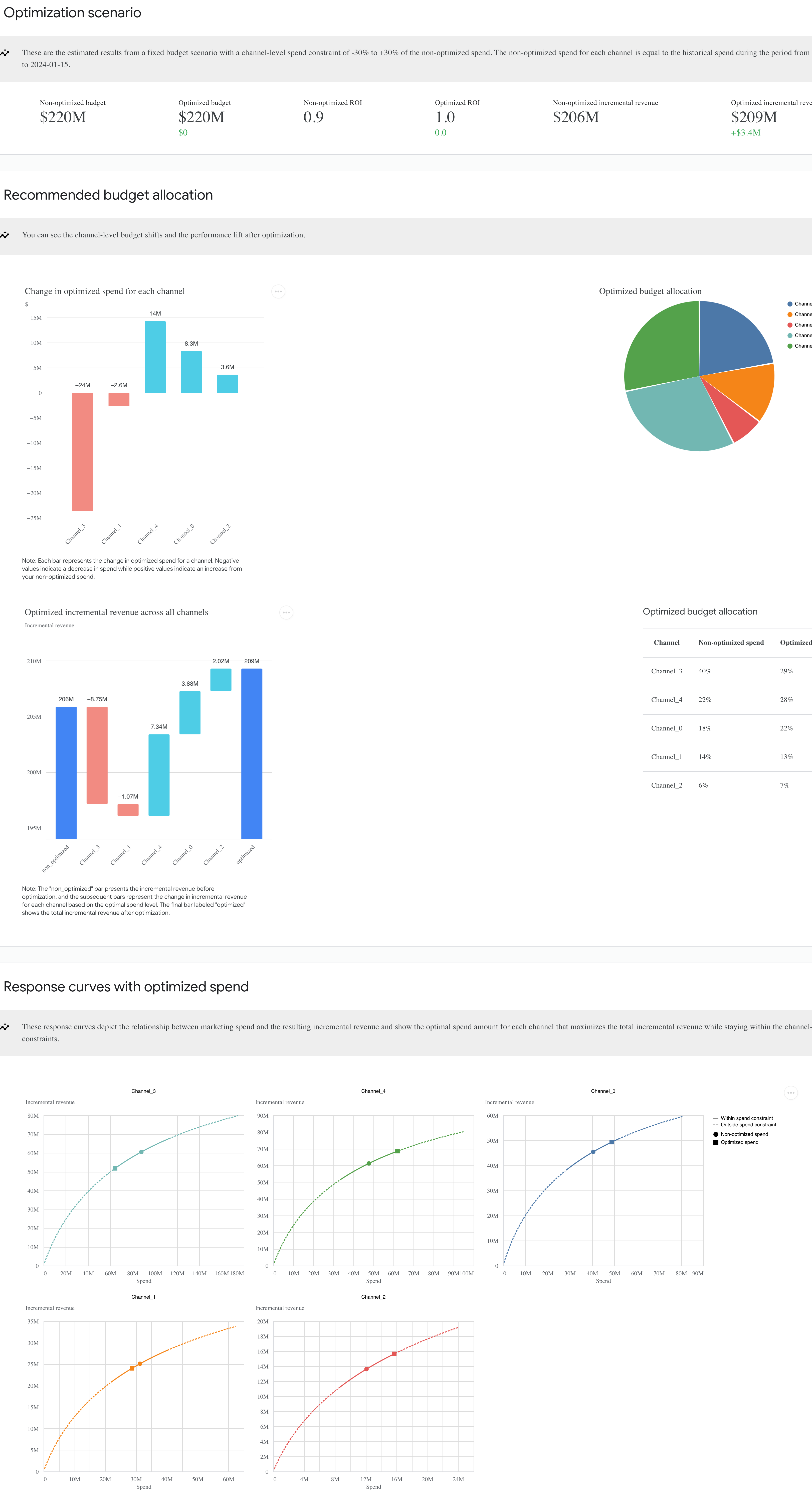
6. 予算配分の最適化
Meridian はモデルの推定結果をベースに予算配分の最適化を行うことも可能です。このステップにはBudgetOptimizerクラスのbudget_optimizerメソッドを使用します。さらに、ouput_optimization_summaryメソッドを使用することで、先ほどと同様にhtmlのレポートを自動的に生成してくれます。
%%time
budget_optimizer = optimizer.BudgetOptimizer(mmm)
optimization_results = budget_optimizer.optimize()
filepath = '/content/drive/MyDrive'
optimization_results.output_optimization_summary('optimization_output.html', filepath)
IPython.display.HTML(filename='/content/drive/MyDrive/optimization_output.html')
7. モデルの保存
最後にモデルを保存します。
file_path='/content/drive/MyDrive/saved_mmm.pkl'
model.save_mmm(mmm, file_path)
最後に
Meridian以前はLightweightMMMが有名でしたが,Meridianは正当な進化・拡張版としてLightweightMMMからの容易な移行が可能です。Meridianのモデル特定に関するドキュメントは若干の読みにくさもあるのですが、本記事がMeridianの理解と実践に役に立つことができれば幸いです。
参考文献
- Borden, N. H. (1964). The concept of the marketing mix. Journal of advertising research, 4 (2), 2-7.
- McCarthy, J. E. (1978), Basic marketing: a managerial approach (6th ed.). Homewood, Il: R.D.
Irwin. - Jin, Y. (2017) et al., Bayesian Methods for Media Mix Modeling with Carryover and Shape Effects, https://research.google/pubs/bayesian-methods-for-media-mix-modeling-with-carryover-and-shape-effects/
- Sun, Y. (2017) et al., Geo-level Bayesian Hierarchical Media Mix Modeling, https://research.google/pubs/geo-level-bayesian-hierarchical-media-mix-modeling/
- Yingxiang, Z. (2024) et al., Media Mix Model Calibration With Bayesian Priors, https://research.google/pubs/media-mix-model-calibration-with-bayesian-priors/
- Yingxiang, Z. (2023), Bayesian Hierarchical Media Mix Model Incorporating Reach and Frequency Data, https://research.google/pubs/bayesian-hierarchical-media-mix-model-incorporating-reach-and-frequency-data/
一緒にお仕事しませんか!
株式会社Nospareではデータサイエンスの様々な分野を専門とする研究者が所属しており,新たな知見を日々追求しています.統計アドバイザリーやビジネスデータの分析につきましては弊社までお問い合わせください.インターンや正社員も随時募集しています!