深層学習が流行りまくっている裏で密かに注目を集めつつあるTopoloical Data Analysis (TDA, 位相的データ解析) というデータ解析手法があります.お気持ちだけでも理解してもらえればと思い,本記事ではTDAの概要についてまとめてみます.数学的な厳密さを求めると1冊の本になってしまうくらい長くなるのでこの記事ではお気持ちの部分しか書きませんのであしからず.
※TDAにはMapperとPersistent Homologyの二つがありますが,Mapperは主にデータの可視化に用いる技術であり,本記事では対象としません.この2つの違いについてはトポロジカルデータアナリシスと時系列データ解析への応用という記事が詳しいです,以下ではTDAはすべてPersistent Homologyの方を指します.
そもそもTDAとは
TDAとは代数的位相幾何学(algebraic topology)という分野を基礎に持つ,データの構造に着目した解析手法であり,画像・たんぱく質のような複雑な構造・ネットワークなどのデータに対して強みを持っています.
2009年にCarlssonらによるTopology and dataという論文で提案されました.
TDAではある意味大雑把にデータの構造を捉え,定性的な特徴を得ることができます.そのため,ノイズに対してロバストである,座標系や次元数に依存しないというメリットがありますが,その反面,そのままの形では分類には適用できても回帰問題には適用しづらいという弱点もあります.
近年ではTDAにおけるカーネル法が提案され,SVMやDNNなどに特徴量として入力するという使い方ができるようになってきており,利用される場面が増えてきています.
代数的位相幾何学のお気持ち
新たに穴を作ったり,穴を潰したりしない連続的な変化によってできる構造はすべて同値である,とするところから出発します.

https://ja.wikipedia.org/wiki/%E4%BD%8D%E7%9B%B8%E5%B9%BE%E4%BD%95%E5%AD%A6
このgifアニメのようにカップとドーナツは穴を作ったり潰したりせずに相互に連続変化で移り変われるので,この二つ(及びその中間の構造)は同値であると言えます.
つまり,代数的位相幾何学では穴の次元や数によって構造を捉えていきます.
具体的には以下のような構造の有無・数を捉えていきます.
- 0次の穴:連結成分
- 1次の穴:"いわゆる"穴
- 2次の穴:空洞
- ・・・
- n次の穴
上のgifアニメに登場するドーナツやカップは0次の穴(連結成分)が1つと1次の穴が1つとカウントします.
TDAの方法
上記のように「穴」の次元や数を捉えるのですが,実際に何らかの構造を構成しているわけではない空間上に散らばるデータ点に対してはこの考え方はそのままでは適用できません.
そこで,データ点を中心とし,中心からの距離が$r$の超球面を考えます.
このrを解像度のパラメータとしてあつかうことで,各解像度におけるデータ点の成す構造を捉えていきます.
このgifアニメのように$r$の値を徐々に大きくしていくことでデータ点の成す構造が変化(穴が誕生したり消滅したり)していきます.
パラメータ$r$に対して穴がどのように誕生と消滅を起こすのかを捉えることで,そのデータ点の構造について情報を得ることができます.
パーシステント図とバーコード
パラメータ$r$に対する穴の誕生と消滅の表現方法としてパーシステント図とバーコードの2つがあり,これらがTDAにより最終的に出力される結果となっています.これらはともに穴の誕生と消滅のタイミングを表現したものであり,(誕生,消滅)の対として扱うことでカーネルに用いたりすることもできます.
パーシステント図
ガウス分布に従う乱数によって生成された2次元上の点100個に対するTDAの結果をパーシステント図で示したものが以下の画像です.
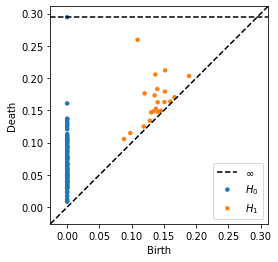
$H_0$は0次の穴を,$H_1$が1次の穴を指しており,第1軸が穴の誕生時のパラメータ$r$の値,第2軸が穴の消滅時のパラメータ$r$の値を示しています.
対角線に近いものは誕生してすぐに消滅してしまうことを表しており,ノイズとみなされることや,あまり重要ではないと考えられることが多いです.実際,カーネルを計算する際も,対角線から遠いものほど重視されるように重み付けされます.
パーシステント図はscikit-tdaというscikit-learn風のpythonモジュールを用いることで簡単に得ることができます.
導入は以下のコマンドでできます.cythonを先にインストールしておかないといけません.
pip install cython
pip install ripser
そして上のパーシステント図は次のようにして生成されます.
import numpy as np
from ripser import ripser
from persim import plot_diagrams
data = np.random.random((100,2))
diagrams = ripser(data)['dgms']
plot_diagrams(diagrams, show=True)
scikit-learnと同じようなインターフェースで非常に簡単に扱うことができます.
バーコード
3つのデータ点におけるバーコードの例を以下に示します(データ点の間には何らかの良い感じの距離が設定されてると思ってください).
パラメータ$r$を5段階に変化させたときの移り変わりを示しており,右に行くほど$r$が大きくなっています.
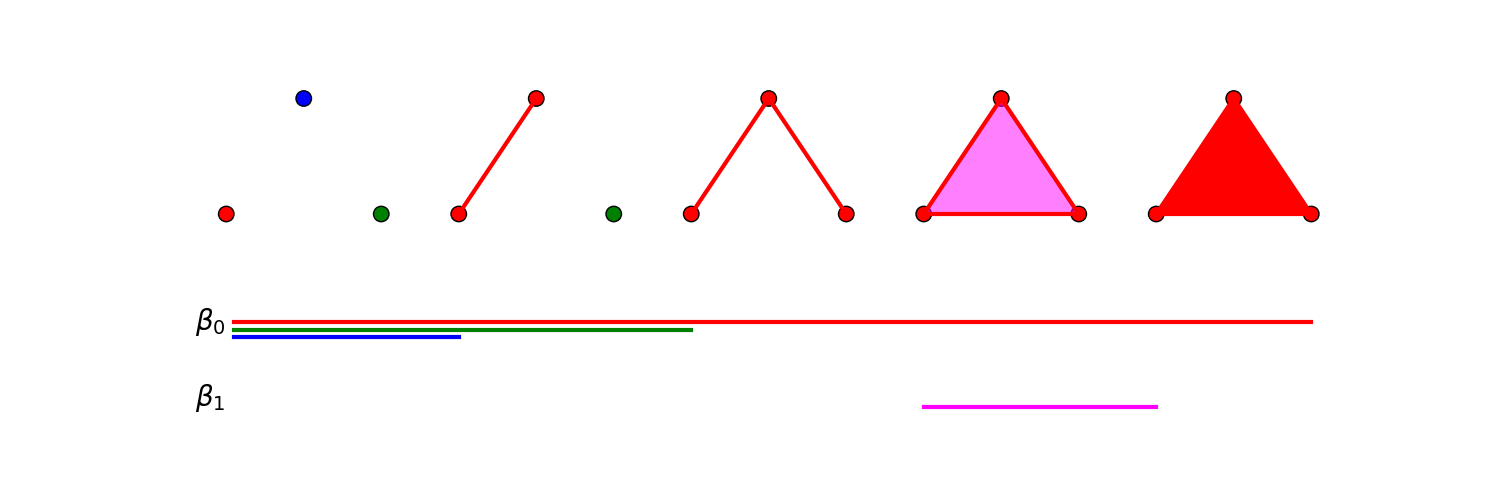
$\beta_0$が0次の穴,$\beta_1$が1次の穴を意味しており,各構造的な要素(点,辺,穴)に対応する色の横棒は左端が誕生のタイミング,右端が消滅のタイミングを表しています.
パーシステント図と表しているものは同じですが,こちらのほうがデータ点のつくる構造との対応が分かりやすいです.しかし,データが増えると無限に下に伸びていくので,実際にはパーシステント図のほうが使いやすく,バーコード図はTDAの概要を説明するときによく用いられている印象があります.
終わりに
数学的な厳密さを排除したら驚くほどゆるふわな記事になってしまいましたが,実際にTDAを使うときは最低限これくらいの理解があれば十分なのではないかなというラインのことは書いたつもりです.
最近ではCNNがどのような特徴を捉えているのかをTDAによって定量的に評価する研究や,DNNの構造をTDAによって評価する研究など,面白い研究が多くあります.
代数ゴリゴリで電気系には少し敷居の高さを感じてしまうTDAを知るきっかけになれば幸いです.
