SinとかSqrt等の算術演算と掛け算の処理負荷を比べてみた #C#

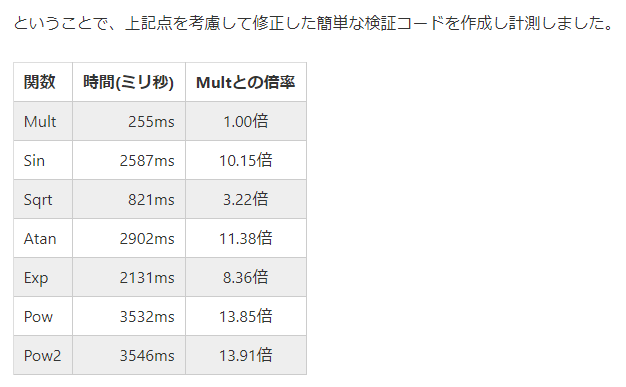
結論：

Pow関数：掛け算の75倍くらい
Exp関数：掛け算の66倍くらい
Atan関数：掛け算の55倍くらい
Sin関数：掛け算の12倍くらい
Sqrt関数：掛け算と同じくらい。たまに掛け算より速い（？？？）

（PCで、UnityのProfilerで計測、C#のMath関数を利用）

注意：

※検証方法により違ってくるところもありますので、この結果は参考までにとどめて、鵜呑みにせずにご自身の環境、利用方法に沿った計測を行ってください。

他の方のによる検証や情報なども寄せられましたので、是非ご参考にしてください。

CPU命令的には，各アーキ毎にどの命令がどのくらいのサイクル数が必要かは文書化されていて，
例えば以下のようなものがありますhttps://t.co/qR8Rk6uT17

ここで重要なのはLatencyとthrough putです．
— 百千万億萬.cpp (@TumoiYorozu_FBC) 2019年2月22日

算術演算って何やってんのかわからん

昨日最適化してて思ったけど、四則演算くらいなら処理負荷まぁこんなもんか、って感覚はあるけど、SqrtとかSinとかAngle（Arcsine）とか実際の処理負荷どんなもんなんだろ（掛け算何回分くらいだろう？）っていうのは知りたい
— じーくどらむす (@geekdrums) 2019年2月20日

最適化しててふと疑問に感じることがありまして。

「ここで掛け算を1000回やってるから重いんだろうけど、Atan使って必要なところを絞って100回に減らしたら、総合的に得なんだろうか……？」と。

Math.○○系の関数って、なんか頑張って近似アルゴリズムとか走らせてるんだろうけど、その中で何回掛け算と同じような処理が走っているのかなんて、なかなか感覚的にはわからないですよね。ググっても良い資料が見当たらず、CPUやライブラリ依存のところがあるから測るしかないと言われ、Unityで軽く測ってみました。

なお、こういう計測や最適化はあまり専門ではないので、測り方がおかしいんじゃねぇの！？っていうマサカリがあれば投げてください。。

右端のカラムがSelf ms、右から2番めがTime msで、2番目の方が関数トータルでのコストです。

なるほど、Sinが掛け算12回分とそこまで致命的ではないのが救いですが、Atanは重いですね、掛け算100回分削れるならアドがあります。

Powの意外なまでの重さにも驚きました。Powは2通り計測していて、Pow(f,f)と、Pow(f,2)で試しましたが、後者は最適化でf*fとかになってくれても良さそうですが、ほぼ変わらず、掛け算の70～75倍ほどのコストがかかっていました。

そして、Sqrtの異常な速さ。Sqrt用のCPU命令があるんですかね……？距離計算でMagnitudeよりSqrMagnitudeの方が軽いのは明白だけど、最後に掛け算一個削る程度の違いしかない模様。

計測は環境やライブラリにも依存していると思うので、他の環境で違った結果出るなら聞きたいです。

今回検証に使ったコードを置いておきます。

MathTest.cs

using System;
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class MathTest : MonoBehaviour
{
    public double count = 1000;
    public double step = 1;

    void Mult()
    {
        double f;

        for( double i = 0; i < count; i += step )
        {
            f = i * i;
        }
    }

    void Sin()
    {
        double f;

        for( double i = 0; i < count; i += step )
        {
            f = Math.Sin(i);
        }
    }

    void Sqrt()
    {
        double f;

        for( double i = 0; i < count; i += step )
        {
            f = Math.Sqrt(i);
        }
    }

    void Pow()
    {
        double f;

        for( double i = 0; i < count; i += step )
        {
            f = Math.Pow(i, i);
        }
    }

    void Pow2()
    {
        double f;

        for( double i = 0; i < count; i += step )
        {
            f = Math.Pow(i, 2);
        }
    }

    void Atan()
    {
        double f;

        for( double i = 0; i < count; i += step )
        {
            f = Math.Atan(i);
        }
    }

    void Exp()
    {
        double f;

        for( double i = 0; i < count; i += step )
        {
            f = Math.Exp(i);
        }
    }

    // Update is called once per frame
    void Update()
    {
        if( step <= 0 )
        {
            return;
        }

        Mult();

        Sin();

        Sqrt();

        Atan();

        Exp();

        Pow();

        Pow2();
    }
}

おまけ

最適化したかったやつ（Atan使って角度の処理範囲を絞った）

2D影メッシュ生成スクリプト、我ながら良く作れたと思う。動かすと楽しい。最適化もまぁまぁできた。 pic.twitter.com/IEfL2owYwg
— じーくどらむす (@geekdrums) 2019年2月18日