1. はじめに
今回は、安定性に優れ、連続制御が可能な強化学習手法であるPPO(Proximal Policy Optimization)をGymnasiumのCar racingに実装してみたいと思います。強化学習の真価が見れると思います!※詳しい理論などは特に解説は行いません。自分の復習も兼ねて記事としていますので、間違っていたらスミマセン…汗
2. Car Racingとは
Car Racingは、Gymnasiumライブラリに含まれる強化学習環境の一つで、トップダウンビューのレースゲームを模したシミュレーションです。この環境は、ピクセルデータから学習するタスクであり、強化学習アルゴリズムのテストや研究に広く利用されています。

- 状態(state)
環境の状態は、96x96ピクセルのRGB画像として提供されます。この画像には、車両の位置、トラックの形状、周囲の情報が含まれています。
状態のイメージ↓
-
行動(action)
連続値アクション: 行動は3つの連続値で制御されます。
1, ステアリング(-1は左に全開、+1は右に全開)
2, アクセル(0から1の範囲)
3, ブレーキ(0から1の範囲) -
報酬(reward)
- トラックタイルの訪問: トラック上のタイルを訪れるごとに報酬が与えられます。
- フレームごとのペナルティ: 各フレームで -0.1 のペナルティが課されます。これにより、効率的な走行が促されます。
- トラック外へのペナルティ: 車がトラック外に出ると、-100 のペナルティが与えられ、エピソードが終了します。
3. ニューラルネットワークの構成
今回PPOに適用させるニューラルネットワーク構成は次のようなイメージで組みました。PPOのネットワーク構造は、強化学習におけるActor-Criticモデルを基盤としています。この構造は、ポリシー(行動方針)と価値関数(状態の良さ)を同時に学習するために設計されています。またinputするデータがゲーム画面(ピクセルデータ)となりますので、CNN(畳み込み層)とFC(全結合層)で構成されています。

インプットする画像はグレースケール化と4スタックとすることで進行方向の情報が加わるようにします。スタックのイメージ↓

4. 実装
環境の作成
def make_env():
env = gym.make("CarRacing-v3", lap_complete_percent=0.95)
env = GrayscaleObservation(env, keep_dim=True) # グレースケール化
env = FrameStackObservation(env, stack_size=4) # 4フレームスタック
return env
Gymnasiumの設定としてグレースケール化と4フレームスタックをすることができました。
action_repeat = 10
image_stack = 4
class Wrapper():
def __init__(self, env):
self.env = env
def reset(self):
self.av_r = self.reward_memory()
img_gray, _ = self.env.reset()
return img_gray
@staticmethod
def reward_memory():
count = 0
length = 100
history = np.zeros(length)
def memory(reward):
nonlocal count
history[count] = reward
count = (count + 1) % length
return np.mean(history)
return memory
def step(self, action):
rewards = 0
for i in range(action_repeat):
next_state, reward, done, truncated, info = self.env.step(action)
reward = round(reward,1)
rewards += reward
truncated2 = True if self.av_r(reward) <= -0.1 else False
if done or truncated or truncated2:
break
return next_state, rewards, done, truncated, truncated2
def close(self):
self.env.close()
さらに環境のカスタムを行います。今回は設定したaction_repeat分だけ同じ動作を繰り返すようにします。今回は10回繰り返します。(これを設定しないとうまく学習が進みませんでした)。あとは報酬設計として、-1点が連続して続いた場合(コース外を走り続けた場合)に強制終了するように設定してあります。
ニューラルネットワーク構成
img_stack = 4
class PPO(nn.Module):
def __init__(self, img_stack):
super(PPO, self).__init__()
self.cnn = nn.Sequential( # input shape (4, 96, 96)
nn.Conv2d(img_stack, 8, kernel_size=4, stride=2),
nn.ReLU(),
nn.Conv2d(8, 16, kernel_size=3, stride=2),
nn.ReLU(),
nn.Conv2d(16, 32, kernel_size=3, stride=2),
nn.ReLU(),
nn.Conv2d(32, 64, kernel_size=3, stride=2),
nn.ReLU(),
nn.Conv2d(64, 128, kernel_size=3, stride=1),
nn.ReLU(),
nn.Conv2d(128, 256, kernel_size=3, stride=1),
nn.ReLU(),
) # output shape (256, 1, 1)
self.v = nn.Sequential(nn.Linear(256, 100), nn.ReLU(), nn.Linear(100, 1))
self.fc = nn.Sequential(nn.Linear(256, 100), nn.ReLU())
self.alpha_head = nn.Sequential(nn.Linear(100, 3), nn.Softplus())
self.beta_head = nn.Sequential(nn.Linear(100, 3), nn.Softplus())
self.apply(self._weights_init)
@staticmethod
def _weights_init(m):
if isinstance(m, nn.Conv2d):
nn.init.xavier_uniform_(m.weight, gain=nn.init.calculate_gain('relu'))
nn.init.constant_(m.bias, 0.1)
def forward(self, x):
x = self.cnn(x)
x = x.view(-1, 256)
v = self.v(x)
x = self.fc(x)
alpha = self.alpha_head(x) + 1
beta = self.beta_head(x) + 1
return (alpha, beta), v
ニューラルネットワークの構成は前述の通りとなっています。また、ニューラルネットワークの初期化としてXavier初期化を適応してあります。
エージェントクラス
MAX_SIZE = 2000
LEARNING_RATE = 0.001
GAMMA = 0.99
EPOCH = 8
BATCH=128
EPS=0.1
transition = np.dtype([('s', np.float64, (img_stack, 96, 96)),
('a', np.float64, (3,)),
('a_logp', np.float64),
('r', np.float64),
('s_', np.float64, (img_stack, 96, 96))])
class Agent():
def __init__(self, device, model):
self.model = model.to(device)
self.device = device
self.buffer = np.empty(MAX_SIZE, dtype=transition)
self.counter = 0
self.training_step = 0
self.optimizer = optim.Adam(self.model.parameters(), lr=LEARNING_RATE)
def select_action(self, state):
state = state.to(device)
with torch.no_grad():
alpha, beta = self.model(state)[0]
dist = Beta(alpha, beta)
action = dist.sample()
a_logp = dist.log_prob(action).sum(dim=1)
action = action.squeeze().cpu().numpy()
a_logp = a_logp.item()
return action, a_logp
def store(self, transition):
self.buffer[self.counter] = transition
self.counter += 1
if self.counter == MAX_SIZE:
self.counter = 0
return True
else:
return False
def update(self):
self.training_step += 1
s = torch.tensor(self.buffer['s'], dtype=torch.float).to(self.device) #(MAX_SIZE, stack, 64, 64), torch.Size([100, 4, 64, 64])
a = torch.tensor(self.buffer['a'], dtype=torch.float).to(self.device) #torch.Size([MAX_SIZE, 3])
r = torch.tensor(self.buffer['r'], dtype=torch.float).to(self.device).view(-1, 1) #torch.Size([MAX_SIZE, 1])
next_s = torch.tensor(self.buffer['s_'], dtype=torch.float).to(self.device)
old_a_logp = torch.tensor(self.buffer['a_logp'], dtype=torch.float).to(self.device).view(-1, 1)
with torch.no_grad():
target_v = r + GAMMA * self.model(next_s)[1]
adv = target_v - self.model(s)[1]
for _ in range(EPOCH):
for index in BatchSampler(SubsetRandomSampler(range(MAX_SIZE)), BATCH, False):
alpha, beta = self.model(s[index])[0]
dist = Beta(alpha, beta)
a_logp = dist.log_prob(a[index]).sum(dim=1, keepdim=True)
ratio = torch.exp(a_logp - old_a_logp[index])
surr1 = ratio * adv[index]
surr2 = torch.clamp(ratio, 1.0 - EPS, 1.0 + EPS) * adv[index]
action_loss = -torch.min(surr1, surr2).mean() #clip付の損失の計算
value_loss = F.smooth_l1_loss(self.model(s[index])[1], target_v[index]) #価値の損失計算
entropy_loss = dist.entropy().mean() #エントロピーの計算
loss = action_loss + 2. * value_loss - 0.01 * entropy_loss #最終の損失関数
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
続いてエージェントクラスです。今回は計算量が膨大となるためGPU(CUDA)を使用する設定としてあります。
-
def select_action(self, state)
car racingのactionは(0~1)で表すことができるので(ステアリングは(-1~1)ですが)、actionの推論はBeta分布を用いて行います。参考論文ではGaussianよりもいい結果が出ています。a_logpは後の損失計算で使用します。 -
def update(self)
PPOの根幹となる更新部分です。最終損失を計算するために、
clip付の損失 action_loss = -torch.min(surr1, surr2).mean()
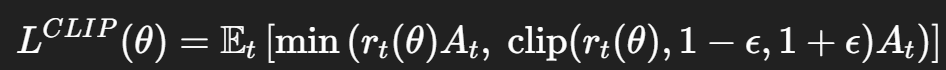
PPOの肝といわれる部分で、clip付の損失とすることで、方策の暴走を緩和することができます。
価値の損失 value_loss = F.smooth_l1_loss(self.model(s[index])[1], target_v[index])

TDターゲットと推論した価値との誤差を計算します。PPOではHuber損失がよく使われるみたいです。
エントロピー entropy_loss = dist.entropy().mean()

エントロピーを加えることで探索性の維持を狙います。
最終損失 loss = action_loss + 2. * value_loss - 0.01 * entropy_loss
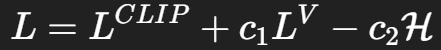
最終的な損失です。c1とc2はハイパーパラメーターで2と0.01としてみました。
学習の繰り返し
そして、収集したデータはバッチサイズに分割してEPOCH数分学習を繰り返します。これもPPOの特徴で、パラメーターが安定して更新される、高い学習性能を出せることにつながっています。
学習のループ
env = make_env()
env_wrapper = Wrapper(env)
model = PPO(image_stack)
agent = Agent(device, model)
episodes = 3000
timestep = 0
reward_history = []
state = env_wrapper.reset()
for episode in range(episodes):
cnt = 0
state = env_wrapper.reset()
total_reward = 0
state = preprocess_state(state)
while True:
action, a_logp = agent.select_action(state)
trans_action = action * np.array([2., 1., 1.]) + np.array([-1., 0., 0.])
next_state, reward, done, trancated, truncated2 = env_wrapper.step(trans_action)
next_state = preprocess_state(next_state)
if agent.store((state, action, a_logp, reward, next_state)):
print("update")
agent.update()
total_reward += reward
state = next_state
cnt += 1
if done or trancated or truncated2:
timestep += 1
break
最後に学習のループを回してエージェントを鍛えていきます。3000エピソード分学習をしてみました。
5. 学習結果
学習時間ですが、一晩かかりました、、やはり画像データを扱うと計算量が大きくなります。
そして、結果です。

学習が進むとともに報酬も上がっています!ただ、後半がおかしい、、とりあえず置いておいて。学習はうまくいった模様です!
学習前↓

学習後↓

コース内をくねくねしながら走っていますが、報酬が高くなるようしっかりと学習できている様子が見えました!
考察
-
走行中の蛇行について
報酬設計が原因かと思われます。今回はコース内を1タイル進むごとに報酬をもらえる設計となっていますので、蛇行したほうが多くの報酬をもらえると学習したと考えられます。より滑らかな運転を目指すには、・コースの中心を走ると報酬UP ・急激なステアリング操作をしたらペナルティ 等の報酬設計を加えると改善すると思います。 -
急激な報酬Down
1200エピソード以降、報酬が一気に0近くまで落ちてしまいました。結果を見てみると、なにやら完全におかしな挙動になってしまいました。
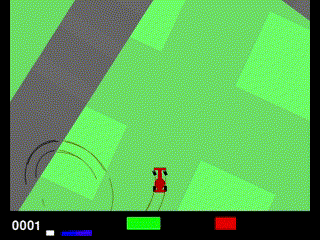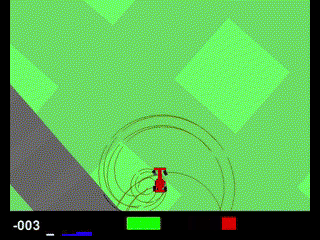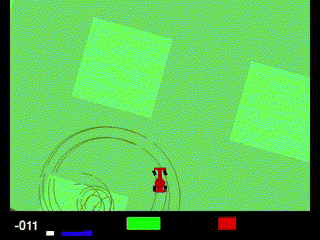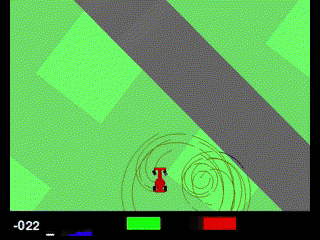
調べてみたのですが、どうやら「Policy collapse(ポリシー崩壊)」というものが起きている可能性が高そうです。PPOなどの方策勾配法でよく起こる問題で、ある瞬間からエージェントが一貫してダメな行動を取るようになり、報酬が回復しなくなる現象なようです。主な要因として、方策の優位性を決めるadvantageの値がおかしくなっていることや、EPOCH数が多すぎて過学習気味になっていることが挙げられています。
この辺は、次回以降の課題として改善できたらと思います。とりあえず今回はPPOを動かすことが目的だったので、満足しております。
6.まとめ
課題はいくつかあったものの、PPOのアルゴリズムがうまく動くのを確認できました。PPOは連続アクションの制御が可能であり、現在ではロボティクスや自動運転、金融など様々な分野に応用されている強力な手法です!ただしハイパーパラメーターのチューニング次第で学習が崩壊してしまうなどの難しさがありますので、なかなか奥が深いものです。
次はこのPPOをつかってより実践的なシミュレーション環境に挑戦していきたいとおもい
参考
1. Proximal Policy Optimization Algorithms
2. Proximal Policy Optimization with Continuous Bounded Action Space via the Beta Distribution
3. Car Racing