三分探索を救いたい

はじめに

前回のAtCoder Beginner Contest151のF問題で最小包含円の問題が出ました。

僕は、ぐーぐる検索の天才なので（おい）

「points cover circle」などと検索して最小包含円にたどり着きコピペをしてしまいました･･･><(そんなことしちゃ、だめだろ)

今回は反省として、F問題での「三分探索」の解法をマスターしていきたいと思います。

三分探索って？

三分探索とは「たかだか一つしか極値のない関数$f$における極値を探索するアルゴリズム」です。

似た概念には、二分探索があります。
この記事やあの記事で解説されています。

今の所まだ三分探索が何をしでかすアルゴリズムかよく分からないので
とりあえず、じっくり見ていくことにします><

関数fの最小値

今回はある区間$[L, R]$における「最小値」を求めることにします。
ある関数$f$における最小値を求めることができれば、それの反対をやれば最大値も求めることができます。

求めたい関数は写真の１の図です。
下に凸っぽい関数であり、一箇所だけ下に凸があります。
（横にへいばいな箇所もありますが、極値が変わっているわけではないので問題ありません。）

この関数の最小値を求めることにします！

大まかな挙動

大まかな挙動を数式なしで説明してみます。

あなたは、左端$low$と右端$high$を持っていて、この内側に一個だけ最小値が存在するようです。
これを効率良く探したいなぁ･･･になっています。

そこで、この左端または右端を少しずつ狭めていくことにしました。
最終的に右端と左端の幅は$0.000000001$ぐらいになり、ほとんど完璧な最小値(近似解)を発見することができます。

ここで、今の左端と右端の区間の長さを$d=high-low$として
もし左端を右に進めて区間を狭めたいときは$low = low + d/3$
もし右端を左に進めて区間を狭めたいときは$high = high - d/3$
とすることにしました。

このように毎回の区間の長さ$d$を求めて$d/3$だけ狭めていくことをすると、$1/3$だけ毎回区間が狭まっていくことになります。
これを繰り返すことによって、最小値を発見することができます。

実際にやってみる

実際に行っている挙動を見たほうが早いので、計算してみることにします。

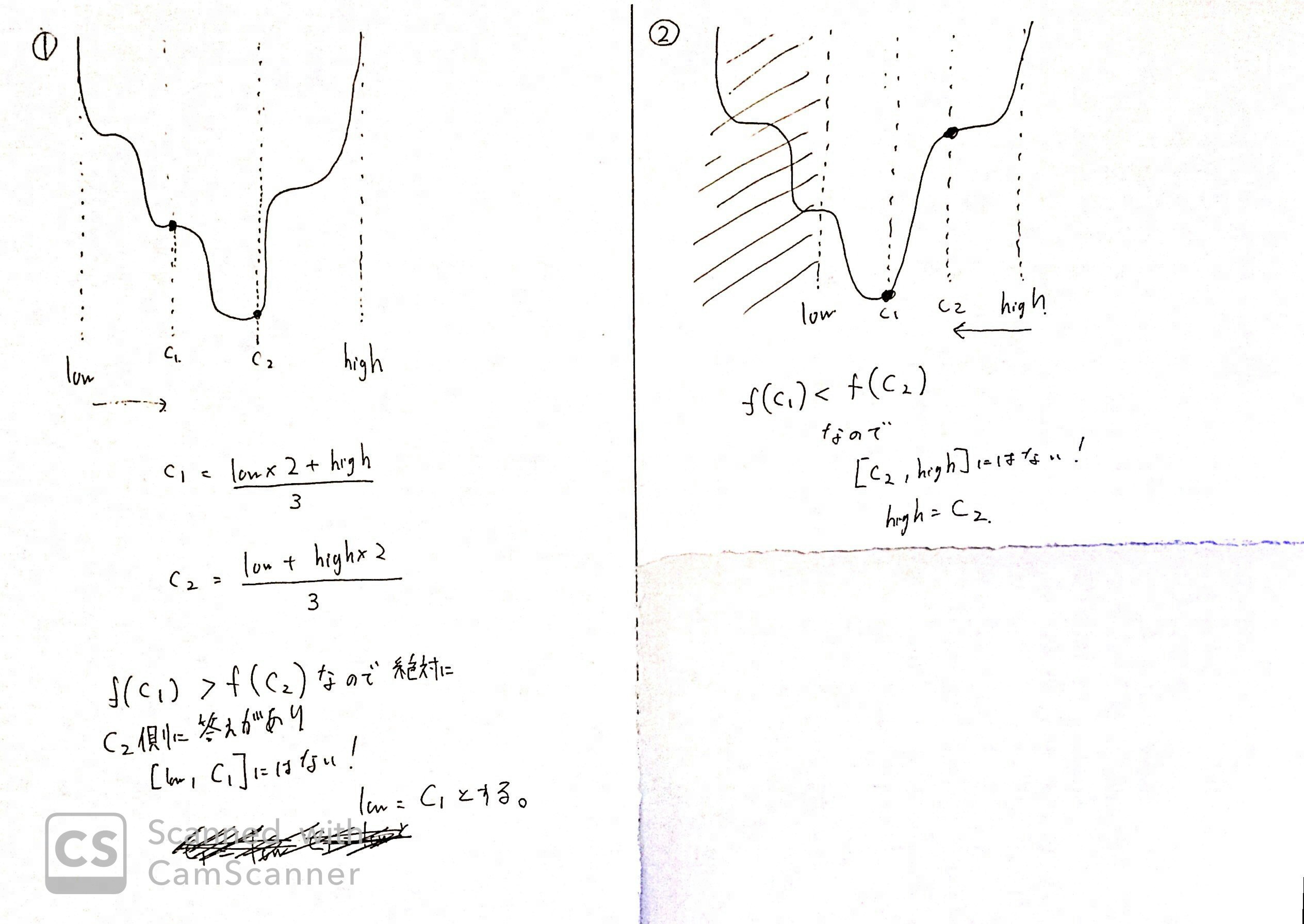
図1

図1では、$low, high$が設定されており、この$[low, high]$の区間にある最小値を発見したいです。
そこで、この区間をまず$3$等分します。

$$c_1 = \frac{low \times 2 + high}{3}$$

$$c_2 = \frac{low + high \times 2}{3}$$

のように計算します。点Aと点Bの内分を行う式から導くことができます。
直感的には、「lowに２つ分、highに1つ分なのが左側の$c_1$!!」みたいな感覚です。

ここで、$f(c_1) > f(c_2)$が成り立っていて、より$c_2$のほうがより小さい値になっています。
よって、$[low, c_1]$の区間に最小値が存在しないことがわかります。
これは、最小値が高々１つのみであり、$f(c_2)$のほうが小さいからです。

よって、$low=c_1$のように駄目なほうを更新し、良い方を残します。

図2

更新された$low, high$の状態でまた再び$c_1, c_2$を計算します。
つまり、$3$等分したときの左側を$c_1$、右側を$c_2$とします。

この結果$f(c_1) < f(c_2)$となり先程は逆の結果になりました。
$c_1$側のほうが値が小さく嬉しいため、$high=c_2$とします。
駄目な方を更新して、良い方を残すイメージです。

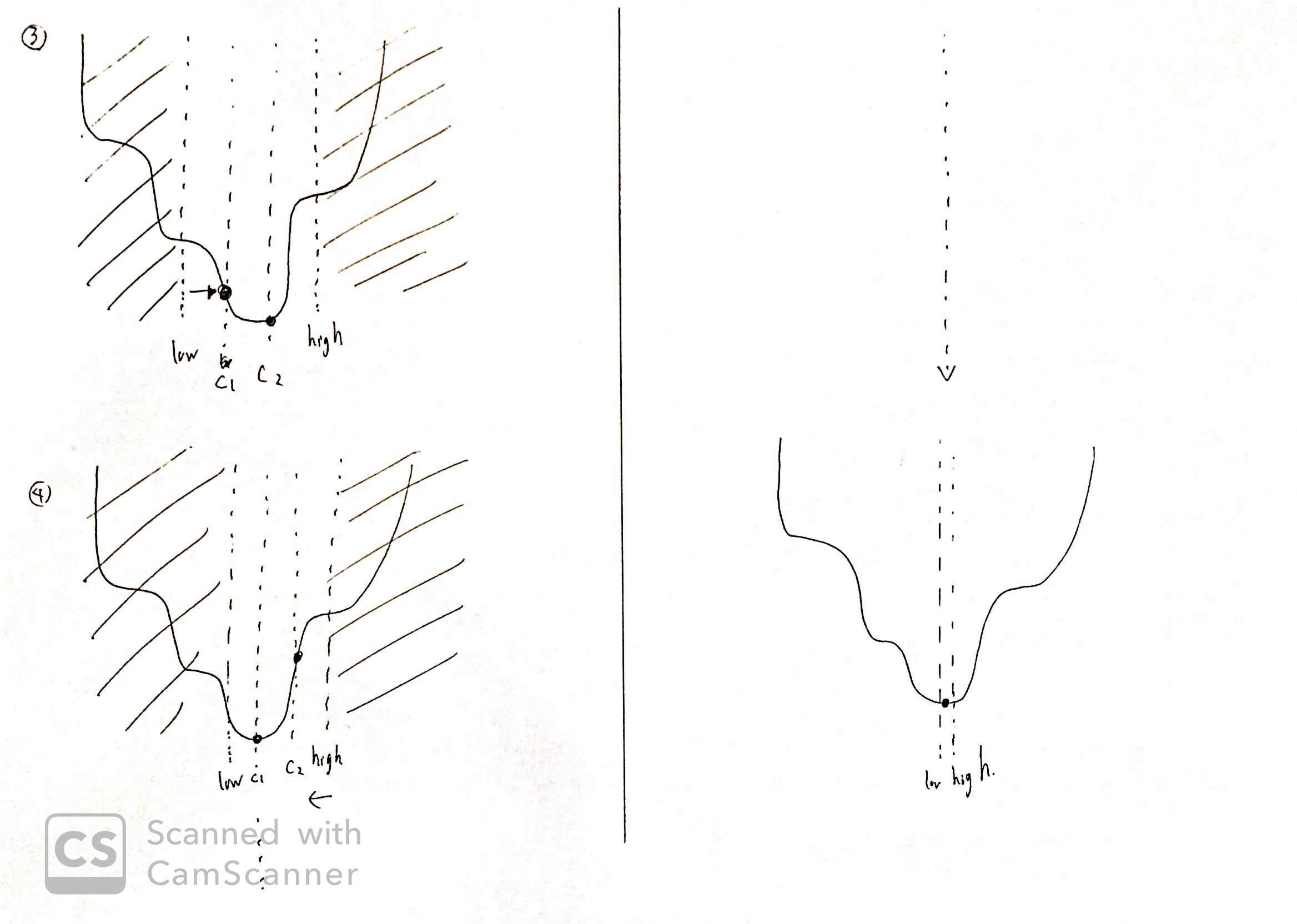
図3と図4

同様に実行していきます。
どんどん狭まっていきます。

最後の図

最終的には、$high-low=1e^{-5}$のようにほとんど同じ地点となり
この極細い区間に答えが存在します。

これは、競技プログラミングでは誤差$1e^{-5}$以下で出力せよのように求められるため
$f(low)$や$f(high)$のどちらかを答えとして出力すれば良いです。

例題を解く

例題としてムーアの法則を解いています。

この問題が言っていることは簡単に書くと以下のようなものです。

$f(x) = x + \frac{P}{2^{\frac{x}{1.5}}}$を最小化せよ。
誤差は$10^{-8}$まで許す。

上記の問題を三分探索で解いてみます。

 
int main() {
 
    double P;
    cin >> P;
 
    // 目的関数(最小化したい)
    auto f = [P](double x) {
        return x + P / pow(2, x / 1.5);
    };
 
    // 左側
    double low = 0;
    // 右側
    double high = 1e9;
 
    // 500回繰り返す
    int cnt = 500;
    while (cnt--) {
        double c1 = (low * 2 + high) / 3;
        double c2 = (low + high * 2) / 3;

        // もしf(c2)のほうが良い(小さい)なら、駄目な方lowを更新する
        if (f(c1) > f(c2)) low = c1;
        else high = c2;
    }
 
    cout << fixed << setprecision(20) << f(low) << endl;
 
}

ソースコードは上記のようになります。

ここで、$low, high$は目的関数$f$の$x$の区間になります。
よって、$[low, high]$の区間にある最適な$x$を求め、そのときの$f(x)$を出力します。

三分探索のコードは

    int cnt = 500;
    while (cnt--) {
        double c1 = (low * 2 + high) / 3;
        double c2 = (low + high * 2) / 3;

        // もしf(c2)のほうが良い(小さい)なら、駄目な方lowを更新する
        if (f(c1) > f(c2)) low = c1;
        else high = c2;
    }

の部分です。

$[low, high]$を$3$等分したときの$c_1, c_2$を比較して駄目な方を更新して、良い方を残します。
今回は最小化を行いたいため、大きい方を更新し小さい方を残します。

ここで、比較するのはfの値ですが、更新するのは座標の$c_1, c_2$であることに注意してください(１敗)。

while(abs(high - low) > 1e-9)のように、誤差が大きい間実行するという手法もありますが
永遠に操作が終わらない場合があるため、規定回数実行するとしたほうが安定して解くことができます。

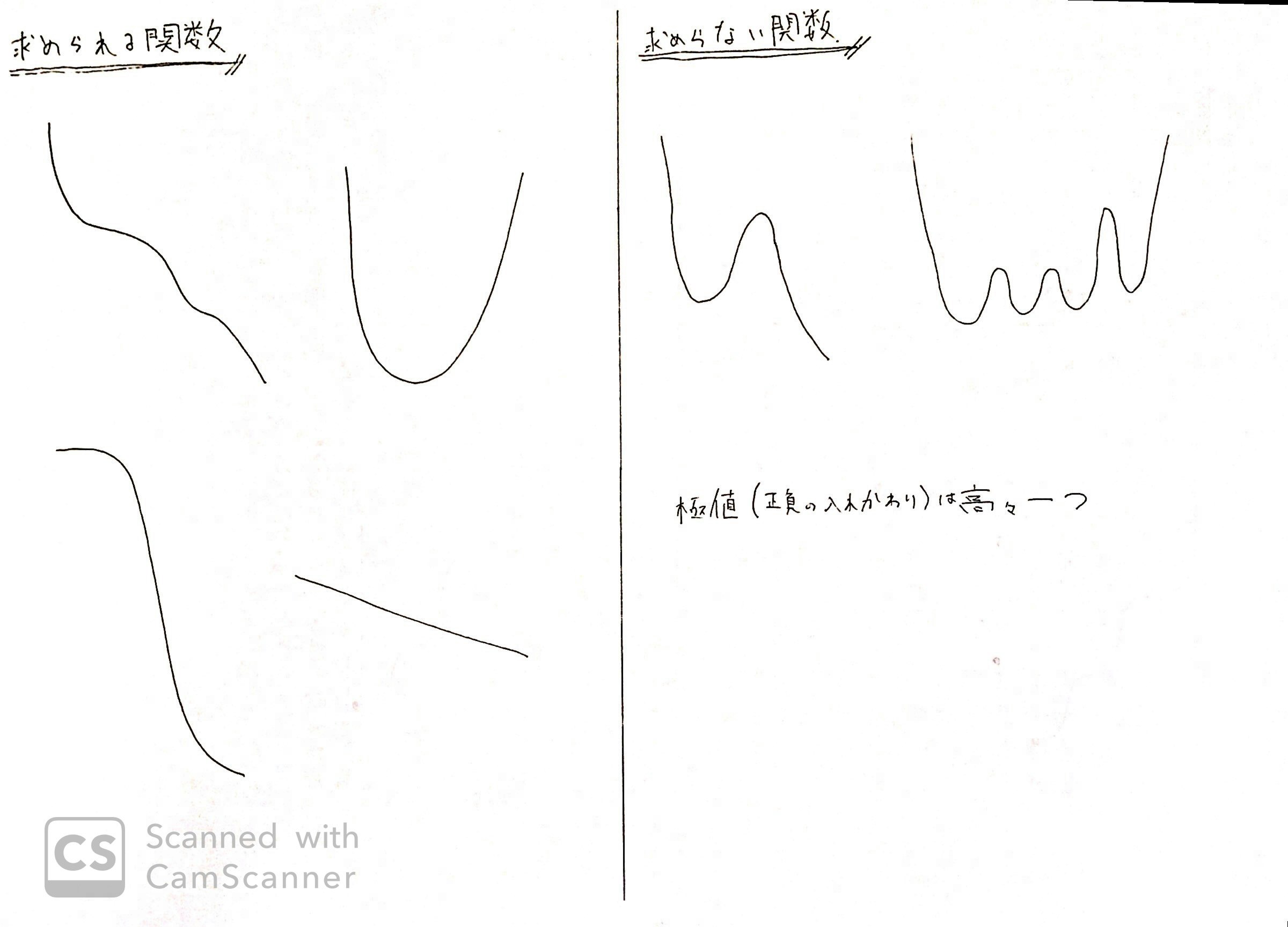
三分探索で扱える関数

三分探索で扱える関数は、「たかだか一つのみ極値が存在するグラフ」になります。

よって、以下のような画像のとおり、極値が複数あると出発点によっては最小化などを発見することができません。
凸性があるかどうかを確認することが大事です。

三分探索を2回行う

最後に、三分探索を2回行う問題を扱います。
というのも、今回のABC151のF問題がその問題でした。

F問題では以下を求めたいです。

$N$個の点が二次元座標にある。この座標において
$f(x, y) = 座標(x, y)$を中心とした円ですべての点を包み込むために必要な半径
を求める関数$f$を定義した時、最小の$f(x, y)$つまり半径を求めよ。

この目的関数$f$は大まかに

のようなグラフになっています。

つまり、2変数をもつ極値が一つしかない凸関数になっています。

このような2変数をもつグラフにおいては、$2$回三分探索を行えばよいです。

1. $x$軸について、$[low_x, high_x]$を定める。
2. $T$回だけ以下を行う。
   3. $x$軸の候補$c_1, c_2$を計算する。このとき、$x=c_1, c_2$のときに最も$f(x, y)$を小さくするような$y$を選びたい。よって、$y$を三分探索することにする。
   4. $y$軸について、$[low_y, high_y]$を定める。
   5. $T$回だけ以下を行う。
   6. $y$軸の候補$c_{1y}, c_{2y}$を計算する。
   7. $f(c_1, c_{1y})$と$f(c_2, c_{2y})$を比較して、悪い方を更新する
   8. 最適な$c_1, c_2$における$y$の値$y_1, y_2$が分かったため、$f(c_1, y_1), f(c_2, y_2)$を計算して悪い方の$x$を更新する
3. $x$の最適値$low_x$が分かったため、$f(low_x, y)$が答え

のように行えばよいです。

詳しくはソースコードを見たほうが早いです><

struct Point {
    Point() : x(0), y(0) {}
    Point(double x, double y) : x(x), y(y) {}
    double x, y;
};

vector<Point> P;

double calc_dist(Point a, Point b) {
    double dx = a.x - b.x;
    double dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
}

double calc_r(Point p) {
    double r = 0;
    for (auto to: P) r = max(r, calc_dist(p, to));
    return r;
}

double calc_y(double x) {
    double low_y = 0;
    double high_y = 1000;
    int cnt = 500;
    while (cnt--) {
        double c1 = (low_y * 2 + high_y) / 3.0;
        double c2 = (low_y + high_y * 2) / 3.0;
        if (calc_r(Point(x, c1)) < calc_r(Point(x, c2))) high_y = c2;
        else low_y = c1;
    }
    return low_y;
}

int main() {

    int N;
    cin >> N;

    P = vector<Point>(N);
    for (int i = 0; i < N; i++) cin >> P[i].x >> P[i].y;

    double low_x = 0;
    double high_x = 1000;
    int cnt = 500;
    while (cnt--) {
        double c1 = (low_x * 2 + high_x) / 3.0;
        double c2 = (low_x + high_x * 2) / 3.0;
        if (calc_r(Point(c1, calc_y(c1))) < calc_r(Point(c2, calc_y(c2)))) high_x = c2;
        else low_x = c1;
    }

    cout << fixed << setprecision(20) << calc_r(Point(low_x, calc_y(low_x))) << endl;

}

最後に

三分探索について、さらっと見てきました。
間違っているところやアドバイスをいただければ嬉しいです><

参考にさせていただいたサイト

• AtCoder ABC 151 F - Enclose All (600 点)
• 三分探索と黄金分割探索
• 三分探索